Chapter 26

Islamic Number Theory and Algebra

It is well known that the numerals used all over the world today are an inheritance from both the Hindu and Arabic mathematicians of 1000 years ago. The Hindu idea of using nine symbols in a place-value system was known in what is now Iraq in the late seventh century, before that area became part of the Muslim Empire. In the late eighth century a scholar from India came to the court of Caliph al-Mansur with a work on Hindu astronomy using these numerals, and this work was translated into Arabic. An Arabic treatise on these numbers, containing the first known discussion of decimal fractions, was written by al-Uqlidisi (ca. 920–ca. 980).

Having inherited works from the time of Mesopotamia and also Greek and Hindu works that used the sexagesimal system in astronomy, the Muslim mathematicians of a thousand years ago also used that system. The sexagesimal system did not yield immediately to its decimal rival, and the technique of place-value computation developed in parallel in the two systems. Ifrah (2000, pp. 539–555) gives a detailed description of the long resistance to the new system. The sexagesimal system is mentioned in Arabic works of Abu'l-Wafa and Kushar ben Laban (ca. 971–1029). It continued to appear in Arabic texts through the time of al-Kashi (1427), although the decimal system also occurs in the work of al-Kashi.¹

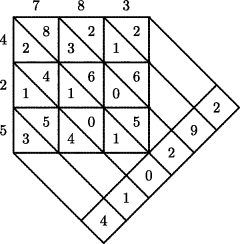
Some implementations of the decimal system require crossing out or erasing in the process of computation, and that was considered a disadvantage. Nevertheless, the superiority of decimal notation in computation was recognized early. For example, al-Daffa (1973, pp. 56–57) mentions that there there are manuscripts still extant dating to the twelfth century, in which multiplication is performed by the very efficient method illustrated in Fig. 26.1 for the multiplication 524 · 783 = 410, 292.

Figure 26.1 The computation 524 × 783 = 410, 292.

26.1 Number Theory

The Muslims continued the work of Diophantus in number theory. Abu Kamil wrote a book on “indeterminate problems” in which he studied quadratic Diophantine equations and systems of such equations in two variables. The first 38 problems that he studied are arranged in order of coefficients, exponents, and signs, making a systematic exposition of these equations. Later scholars noted the astonishing fact that the first 25 of these equations are what are now known as algebraic curves of genus 0, while the last 13 are of genus 1, even though the concept of genus of an algebraic curve is a nineteenth-century invention (Baigozhina, 1995).

Muslim mathematicians also went beyond what is in Euclid and Nicomachus, generalizing perfect numbers. In a series of articles, Rashed [see, for example, Rashed (1989)] pointed out that a large amount of theory of abundant, deficient, and perfect numbers was assembled in the ninth century by Thabit ibn-Qurra and others and that ibn al-Haytham (965–1040) was the first to state and attempt to prove that Euclid's formula gives all the even perfect numbers. Thabit ibn Qurra made an interesting contribution to the theory of amicable numbers. A pair of numbers is said to be amicable if each is the sum of the parts (proper divisors) of the other. The smallest such pair of numbers is 220 and 284. Although these numbers are not discussed by Euclid or Nicomachus, the commentator Iamblichus (see Dickson, 1919, p. 38) ascribed this notion to Pythagoras, who is reported as saying, “A friend is another self.” This definition of a friend is given by Aristotle in his Nicomachean Ethics (Bekker, 2000).

In Chapter 9, we discussed the only known way of generating perfect numbers, namely the Euclidean formula 2ⁿ⁻¹(2ⁿ − 1), whenever 2ⁿ − 1 is a prime. Thabit ibn-Qurra found a similar way of generating pairs of amicable numbers. His formula is

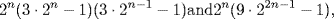
whenever 3 · 2ⁿ − 1, 3 · 2ⁿ⁻¹ − 1, and 9 · 2²ⁿ⁻¹ − 1 are all prime. The case n = 2 gives the pair 220 and 284. Whatever one may think about the impracticality of amicable numbers, there is no denying that Thabit's discovery indicates very profound insight into the divisibility properties of numbers. It is very difficult to imagine how he could have discovered this result. A conjecture, which cannot be summarized in a few lines, can be found in the article by Brentjes and Hogendijk (1989).

It is not clear how many new cases can be generated from this formula, but there definitely are some. For example, when n = 4, we obtain the amicable pair 17, 296 = 16 · 23 · 47 and 18, 416 = 16 · 1151. Hogendijk (1985) gives Thabit ibn-Qurra's proof of his criterion for amicable numbers and points out that the case n = 7 generates the pair 9,363,584 and 9,437,056, which first appeared in Arabic texts of the fourteenth century.

Unlike some other number-theory problems such as the Chinese remainder theorem, which arose in a genuinely practical context, the theory of amicable numbers is an offshoot of the theory of perfect numbers, which was already a completely “useless” topic from the beginning. It did not seem useless to the people who developed it, however. According to M. Cantor (1880, p. 631), the tenth-century mystic al-Majriti recommended as a love potion writing the numbers on two sheets of paper and eating the number 284, while causing the beloved to eat the number 220. He claimed to have verified the effectiveness of this charm by personal experience! Dickson (1919, p. 39) mentions the Jewish scholar Abraham Azulai (1570–1643), who described a work purportedly by the ninth-century commentator Rau Nachshon, in which the gift of 220 sheep and 220 goats that Jacob sent to his brother Esau as a peace offering (Genesis 32:14) is connected with the concept of amicable numbers.² In any case, although their theory seems more complicated, amicable numbers are easier to find than perfect numbers. Euler alone found 62 pairs of them (see Erds and Dudley, 1983).

Another advance on the Greeks can be found in the work of Kamal al-Din al-Farisi, a Persian mathematician who died around 1320. According to Aargün and Fletcher (1994), he wrote the treatise Memorandum for Friends Explaining the Proof of Amicability, whose purpose was to give a new proof of Thabit ibn-Qurra's theorem. Proposition 1 in this work asserts the existence (but not uniqueness) of a prime decomposition for every number. Propositions 4 and 5 assert that this decomposition is unique, that two distinct products of primes cannot be equal.

26.2 Algebra

It has always been recognized that Europe received algebra from the Muslims. As we have already said, the word algebra (al-jabr) is an Arabic word meaning completion or restoration.³ Its origins in the Muslim world date from the ninth century, in the work of al-Khwarizmi, as is well established.⁴

What is less certain is how much of al-Khwarizmi's algebra was original with him and how much he learned from Hindu sources. According to Colebrooke (1817, pp. lxiv–lxxx), he was well versed in Sanskrit and translated a treatise on Hindu computation⁵ into Arabic at the request of Caliph al-Mamun. Colebrooke cites the Italian writer Pietro Cossali,⁶ who presented the alternatives that al-Khwarizmi learned algebra either from the Greeks or the Hindus and opted for the Hindus. These alternatives are a false dichotomy. We need not conclude that al-Khwarizmi took everything from the Hindus or that he invented everything himself. It is very likely that he expounded some material that he read in Sanskrit and added his own ideas to it. Rosen (1831, p. x) explains the difference in the preface to his edition of al-Khwarizmi's algebra text, saying that “at least the method which he follows in expounding his rules, as well as in showing their application, differs considerably from that of the Hindu mathematical writers.”

Colebrooke also notes (p. lxxi) that Abu'l-Wafa wrote a translation or commentary on the Arithmetica of Diophantus. This work, however, is now lost. Apart from these possible influences of Greek and Hindu algebra, whose effect is difficult to measure, it appears that the progress of algebra in the Islamic world was an indigenous growth. We shall trace that growth through several of its most prominent representatives, starting with the man recognized as its originator, Muhammad ibn Musa al-Khwarizmi.

26.2.1 Al-Khwarizmi

Besides the words algebra and algorithm, there is a common English word whose use is traceable to Arabic influence (although it is not an Arabic word), namely root in the sense of a square or cube root or a root of an equation. The Greek picture of the square root was the side of a square, and the word side (pleurá) was used accordingly. The Muslim mathematicians apparently thought of the root as the part from which the equation was generated and used the word jadhr accordingly. According to al-Daffa (1977, p. 80), translations into Latin from Greek use the word latus while those from Arabic use radix. In English the word side lost out completely in the competition.

Al-Khwarizmi's numbers correspond to what we call positive real numbers. Theoretically, such a number could be defined by any convergent sequence of rational numbers, but in practice some rule is needed to generate the terms of the sequence. For that reason, it is more accurate to describe al-Khwarizmi's numbers as positive algebraic numbers, since all of his numbers are generated by equations with rational coefficients. The absence of negative numbers prevented al-Khwarizmi from writing all quadratic equations in the single form “squares plus roots plus numbers equal zero” (ax² + bx + c = 0). Instead, he had to consider three basic cases and two others, in which either the square or linear term is missing. He described the solution of “squares plus roots equal numbers” by the example of “a square plus 10 roots equal 39 dirhems.” (A dirhem is a unit of money.) Al-Khwarizmi's solution of this problem is to draw a square of unspecified size (the side of the square is the desired unknown) to represent the square (Fig. 26.2). To add 10 roots, he then attaches to each side a rectangle of length equal to the side of the square and width 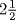(since 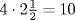). The resulting cross-shaped figure has, by the condition of the problem, area equal to 39. He then fills in the four corners of the figure (literally “completing the square”). The total area of these four squares is 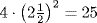. Since 39 + 25 = 64, the completed square has side 8. Since this square was obtained by adding rectangles of side 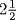to each side of the original square, it follows that the original square had side 3.

Figure 26.2 Al-Khwarizmi's solution of “square plus 10 roots equals 39 dirhems.”

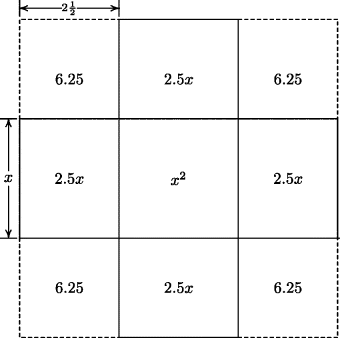
This case is the one al-Khwarizmi considers first and is the simplest to understand. His figures for the other two cases of quadratic equations are more complicated, but all are based on a geometric illustration of the identity ((a + b)/2)² − ((a − b)/2)² = ab.

Al-Khwarizmi did not consider any cubic equations. Roughly the first third of the book is devoted to various examples of pure mathematical problems leading to quadratic equations, causing the reader to be somewhat skeptical of his claim to be presenting the material needed in commerce and law. There are no genuine applications of quadratic equations in the book. Although quadratic equations have no practical applications (outside of technology, of course), there are occasions when a practical problem requires solving linear equations. Al-Khwarizmi found many such cases in problems of inheritance, which occupy more than half of his Algebra. Here is a sample:

A man dies, leaving two sons behind him, and bequeathing one-fifth of his property and one dirhem to a friend. He leaves 10 dirhems in property and one of the sons owes him 10 dirhems. How much does each legatee receive?

Although mathematics is cross-cultural, its applications are specific to the culture in which they are used. The difference between the modern solution of this legal problem and al-Khwarizmi's solution is considerable. Under modern law the man's estate would be considered to consist of 20 dirhems, the 10 dirhems cash on hand, and the 10 dirhems owed by one of the sons. The friend would be entitled to 5 dirhems (one-fifth plus one dirhem), and the indebted son would owe the estate 10 dirhems. His share of the estate would be one-half of the 15 dirhems left after the friend's share is taken out, or 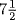dirhems. He would therefore have to pay 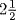dirhems to the estate, providing it with cash on hand equal to 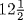dirhems. His brother would receive 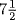dirhems.

Now the notion of an estate as a legal entity that can owe and be owed money is a modern European one, alien to the world of al-Khwarizmi. Apparently, in al-Khwarizmi's time, money could be owed only to a living person. What principles are to be used for settling accounts in this case? Judging from the solution given by al-Khwarizmi, the estate is to consist of the 10 dirhems cash on hand, plus a certain portion (not all) of the debt the second son owed to his deceased father. This “certain portion” is the unknown in a linear equation and is the reason for invoking algebra in the solution. It is to be chosen so that when the estate is distributed, the indebted son neither receives any more money nor owes any to the other heirs. This condition leads to a linear equation. Al-Khwarizmi explains the solution as follows (we put the legal principle that provides the equation in capital letters):

Call the amount taken out of the debt thing. Add this to the property; the sum is 10 dirhems plus thing. Subtract one-fifth of this, since he has bequeathed one-fifth of his property to the friend. The remainder is 8 dirhems plus 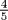of thing. Then subtract the 1 dirhem extra that is bequeathed to the friend. There remain 7 dirhems and 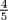of thing. Divide this between the two sons. The portion of each of them is 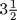dirhems plus 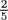of thing. THIS MUST BE EQUAL TO THING. Reduce it by subtracting of thing from thing. Then you have 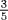of thing equal to 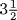dirhems. Form a complete thing by adding to this quantity 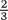of itself. Now 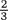of 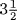dirhems is 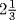dirhems, so that thing is 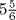dirhems.

Rosen (1831, p. 133) suggested that the many arbitrary principles used in these problems were introduced by lawyers to protect the interests of next-of-kin against those of other legatees.

26.2.2 Abu Kamil

A commentary on al-Khwarizmi's Algebra was written by Abu Kamil.⁷ His exposition of the subject contained none of the legacy problems found in al-Khwarizmi's treatise, but after giving the basic rules of algebra, it listed 69 problems to be solved. For example, a paraphrase of Problem 10 is as follows:

The number 50 is divided by a certain number. If the divisor is increased by 3, the quotient decreases by 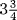. What is the divisor?

Abu Kamil is also noteworthy because many of his problems were copied by Leonardo of Pisa, one of the first to introduce the mathematics of the Muslims into Europe.

26.2.3 Omar Khayyam

Although al-Khwarizmi did not consider any equations of degree higher than 2, such equations were soon to be considered by Muslim mathematicians. A link between geometry and algebra appeared in the use of the rectangular hyperbola by Pappus to carry out the neÛsis construction for trisecting an angle (see Section 3 of Chapter 11). Omar Khayyam (see Amir-Moez, 1963) realized that a large class of geometric problems of this type led to cubic equations that could be solved using conic sections. His treatise on algebra⁸ was largely occupied with the classification and solution of cubic equations by this method. Before we discuss a general cubic equation solved by Omar Khayyam, we note one particular equation of this type that he posed and solved (Amir-Moez, 1963). That problem is to find the point on a circle such that the perpendicular from the point to a radius has the same ratio to the radius that the two segments into which it divides the radius have to each other.

If the radius is r and the length of the longer segment cut off on the radius is the unknown x, the equation to be satisfied is x³ + rx² + r²x = r³. Without actually writing out this equation, Omar Khayyam showed that the geometric problem amounted to using the stated condition to find the second asymptote of a rectangular hyperbola, knowing one of its asymptotes and one point on the hyperbola. However, he regarded that analysis as merely an introduction to his real purpose, which was a discussion of the kinds of cubic equations that require conic sections for their solution. After a digression to classify these equations, he returned to the original problem and, finally, showed how to solve it using a rectangular hyperbola. He found the arc to be about 57°, so that x ≈ r cos (57°) = 0.544r. Omar Khayyam described x as being about 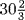pieces, that is, sixtieths of the radius.

Omar Khayyam did not have modern algebraic symbolism. Experience had evidently taught him that attempts to solve the general cubic equation by arithmetic and root extractions would not work in general. But he discovered that such an equation could be interpreted geometrically and solved by the use of conic sections. In applying those conic sections, he wrote in the language of Apollonius and Euclid, with the single exception of representing the lines as numbers. His classification of equations, like al-Khwarizmi's, is conditioned by the use of only positive numbers as data. For that reason his classification is even more complicated than al-Khwarizmi's, since he is considering cubic equations as well as quadratics. He lists 25 types of equations (Kasir, 1931, pp. 51–52), six of which do not involve any cubic terms.

By way of illustration, we shall consider the case of cubes plus squares plus sides equal number, or, as we would phrase it, x³ + ax² + bx = c. In keeping with his geometric interpretation of magnitudes as line segments, Omar Khayyam had to regard the coefficient b as a square, so that we shall write b² rather than b. Similarly, he regarded the constant term as a solid, which without any loss of generality he considered to be a rectangular prism whose base was an area equal to the coefficient of the unknown. In keeping with this reduction we shall write b²c instead of c. Thus Omar Khayyam was considering the equation x³ + ax² + b²x = b²c, where a, b, and c are data for the problem, to be represented as lines. His solution is illustrated in Fig. 26.3. He drew a pair of perpendicular lines intersecting at a point O and marked off OA = a and OC = c in opposite directions on one of the lines and OB = b on the other line. He then drew a semicircle having AC as diameter, the line DB through B perpendicular to OB (parallel to AC), and the rectangular hyperbola through C having DB and the extension of OB as asymptotes. This hyperbola intersects the semicircle in the point C and in a second point Z. From Z he drew ZP perpendicular to the extension of OB. This line ZP represented the solution of the cubic.

Figure 26.3 Omar Khayyam's solution of x³ + ax² + b²x = b²c.

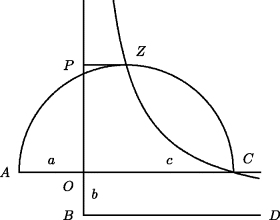
When it comes to actually producing a root by numerical procedures, Omar Khayyam's solution is circular, a mere restatement of the problem. He has broken the cubic equation into two quadratic equations in two unknowns, but any attempt to eliminate one of the two unknowns merely leads back to the original problem. In fact, no method of solution exists or can exist that reduces the solution of every cubic equation with real roots to the extraction of real square and cube roots of real numbers. What Omar Khayyam had created was an analysis of cubic equations using conic sections. He said that no matter how hard you look, you will never find a numerical solution “because whatever is obtained by conic sections cannot be obtained by arithmetic” (Amir-Moez, 1963, p. 336).

26.2.4 Sharaf al-Din al-Tusi

A generation after the death of Omar Khayyam, Sharaf al-Din al-Tusi wrote a treatise on equations in which he analyzed the cubic equation using methods that are surprisingly modern in appearance. This work has been discussed by Hogendijk (1989). Omar Khayyam had distinguished the eight types of cubic equations that always have a solution and five that could fail to have a solution. Al-Tusi provided a numerical method of solution for the first eight types that was essentially the Chinese method of solving cubic equations. He then turned to the five types that might have no (positive) solutions for some values of the data. As an example, one of these forms is

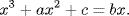
For each of these cases, al-Tusi considered a particular value of x, which for this example is the value m satisfying

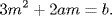
Let us denote the positive root of this equation (the larger root, if there are two) by m. The reader will undoubtedly have noticed that the equation can be obtained by differentiating the original equation and setting x equal to m. The point m is thus in all cases a relative minimum of the difference of the left-and right-hand sides of the equation. That is precisely the property that al-Tusi wanted. Hogendijk comments that it is unlikely that al-Tusi had any concept of a derivative. In fact, the equation for m can be derived without calculus, by taking m as the value at which the minimum occurs, subtracting the values at x from the value at m, and dividing by m − x. The result is the inequality m² + mx + x² + a(m + x) > b for x > m and the opposite inequality for x < m. Therefore equality must hold when x = m, that is, 3m² + 2am = b, which is the condition given by al-Tusi.⁹ After finding the point m, al-Tusi concluded that there will be no solutions if the left-hand side of the equation is larger than the right-hand side when x = m. There will be one unique solution, namely x = m if equality holds there. That left only the case in which the left-hand side was smaller than the right-hand side when x = m. For that case, he considered the auxiliary cubic equation

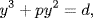
where p and d were determined by the type of equation. The quantity d was the difference between the right-and left-hand sides of the equation at x = m, that is, bm − m³ − am² − c in the present case, with p equal to 3m + a. Al-Tusi was replacing x with y = x − m here. The procedure was precisely the method we know as Horner's method, and the linear term drops out because the condition by which m was chosen ordains that it be so. The equation in y was known to have a root because it was one of the other 13 types, which always have solutions. Thus, it followed that the original equation must also have a solution, x = m + y, where y was the root of the new equation. The added bonus was that a lower bound on m was obtained.

Problems and Questions

Mathematical Problems

26.1 Solve the following legacy problem from al-Khwarizmi's Algebra: A woman dies and leaves her daughter, her mother, and her husband, and she bequeaths to some person as much as the share of her mother and to another as much as one-ninth of her entire capital. Find the share of each person. It was understood from legal principles that the mother's share would be 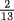and the husband's .

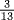26.2 Solve the problem of Abu Kamil in the text.

26.3 Consider the cubic equation of Sharaf al-Tusi's third type, which we write as x³ + ax² − bx + c = 0. Using the Chinese/Horner's method described in Chapter 22, show that if the first approximation is x = m, where m satisfies 3m² + 2am − b = 0, then the equation to be satisfied at the second approximation is y³ + (3m + a)y² + (m³ + am² − bm + c) = 0. That is, carry out the algorithm for reduction and show that the process is

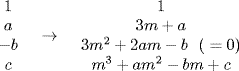
Historical Questions

26.4 What is the subject matter of al-Khwarizmi's Algebra, and what applications does it include?

26.5 How did Omar Khayyam solve cubic equations geometrically, and why does he adopt the geometric approach rather than a numerical one?

26.6 What refinements to the solution of the cubic equation are due to Sharaf al-Din al-Tusi?

Questions for Reflection

26.7 Why did al-Khwarizmi include a complete discussion of the solution of quadratic equations in his treatise when he had no applications for them at all?

26.8 Contrast the modern Western solution of the Islamic legacy problem discussed in the text with the solution of al-Khwarizmi. Is one solution “fairer” than the other? Can mathematics make any contribution to deciding what is fair?

26.9 Why did Omar Khayyam express the answer to a problem involving circles in pieces equal to one-sixtieth of the radius?

Notes

1. In addition to the sexagesimal and decimal systems, the Muslim mathematicians used an elaborate system of finger reckoning.

2. The peace offering was necessary because Jacob had tricked Esau out of his inheritance. But if the gift was symbolic and associated with amicable numbers, this interpretation seems to imply that Esau was obligated to give Jacob 284 sheep and 284 goats. Perhaps there was an ulterior motive in the gift!

3. Gandz (1926) presented a different theory of the origin of the term algebra, according to which the word is not even of Arabic origin, despite its Arabic appearance. To the extent that the majority rules in such matters, this alternative theory is heavily outvoted by the one just described.

4. Colebrooke (1817, p. lxxiii) noted that a manuscript of this work dated 1342 was in the Bodleian Library at Oxford. Obviously, this manuscript could not be checked out, and Colebrooke complained that the library's restrictions “preclude the study of any book which it contains, by a person not enured to the temperature of apartments unvisited by artificial warmth.” If he worked in the library in 1816, his complaint would be understandable: Due to volcanic ash in the atmosphere, there was no summer that year. This manuscript is the source that Rosen (1831) translated and reproduced.

5. It is apparently this work that brought al-Khwarizmi's name into European languages in the form algorism, now algorithm. A Latin manuscript of this work in the Cambridge University Library, dating to the thirteenth century, has been translated into English (Crossley and Henry, 1990).

6. Cossali's dates are 1748–1813. He was Bishop of Parma and author of Origine, trasporto in Italia, primi progressi in essa dell’ algebra (The Origins of Algebra and Its Transmission to Italy and Early Advancement There), published in Parma in 1797.

7. A commentary on the commentary was written in Hebrew by the Italian Jewish scholar Mordecai Finzi (1440–1475). The present example is taken from the English translation of that work (Levey, 1966).

8. This treatise was little noticed in Europe until a French translation by Franz Woepcke (1827–1864) appeared in 1851 (Kasir, 1931, p. 7).

9. This way of finding the minimum was also used by Fermat in the seventeenth century.