Chapter 37

Algebra from 1600 to 1850

By the mid-seventeenth century, the relation between the coefficients and roots of a general equation was understood, and it was conjectured that if you counted roots according to multiplicity and allowed complex roots, an equation of degree n would have n roots. Algebra had been consolidated to the point that the main unsolved problem, the solution of equations of degree higher than 4, could be stated simply and analyzed.

The solution of this problem took nearly two centuries, and it was not until the late eighteenth and early nineteenth centuries that enough insight was gained into the process of determining the roots of an equation from its coefficients to prove that arithmetic operations and root extractions were not sufficient for this purpose. Although the solution was a negative result, it led to the important concepts of modern algebra that we know as groups, rings, and fields; and these, especially groups, turned out to be applicable in many areas not directly connected with algebra. Also on the positive side, nonalgebraic methods of solving higher-degree equations were found, along with a criterion to determine whether or not a prescribed set of roots can be expressed algebraically in terms of the coefficients of the equation that they satisfy.

37.1 Theory of Equations

Viète understood something of the relation between the roots and the coefficients of some equations. His understanding was not complete, because he was not able to find all the roots. Before the connection could be made completely, there had to be a domain in which an equation of degree n would have n roots. Such a domain is called an algebraically closed field. Then the general connection between coefficients and roots could be made for quadratic, cubic, and quartic equations and generalized from there. The missing theorem was eventually to be called the fundamental theorem of algebra.¹

37.1.1 Albert Girard

This fundamental theorem was first stated by Albert Girard (1595–1632), the editor of the works of Simon Stevin. In 1629 he wrote L'invention nouvelle en l'algèbre [New Discovery (Invention) in Algebra]. This work contained some of the unifying concepts that make modern algebra the compact, efficient system that it now is. One of these ideas is to regard the constant term as the coefficient of the zeroth power of the unknown. He introduced the notion of factions of a finite set of numbers. The first faction is the sum of the numbers, the second one is the sum of all products of two distinct numbers from the set, and so on. The last faction is the product of all the numbers, so that “there are as many factions as there are numbers given.” He noted that the number of terms in each faction could be found by using Pascal's triangle.

Girard always regarded the leading coefficient as 1. Putting the equation into this form, he stated as a theorem (see, for example, Struik, 1986, p. 85) that “all equations of algebra receive as many solutions as the denomination [degree] of the highest form shows, except the incomplete, and the first faction of the solutions is equal to the number of the first mixed [that is, the coefficient of the power one less than the degree of the equation], their second faction is equal to the number of the second mixed, their third to the third mixed, and so on, so that the last faction is equal to the closure [product], and this according to the signs that can be observed in the alternate order.” This recognition that the coefficients of a polynomial are elementary symmetric polynomials in its zeros was the first ray of light at the dawn of modern algebra.

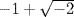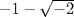By “incomplete,” Girard seems to have meant equations with some terms missing. In some cases, he said, these may not have a full set of solutions. He gave the example of the equation x⁴ = 4x − 3, whose solutions he gave as 1, 1, , and , showing that he realized the need to count both complex roots and multiple real roots for the sake of the general rule. It is not clear what connection he made between missing terms and a reduced number of solutions. If an equation p(x) = 0 with real coefficients has a pure imaginary solution 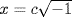, then p(x) is divisible by x² + c², and there will be missing terms. But there may be terms missing even in an equation with a full set of solutions, for example, x⁴ − 13x² + 36; and there may be no missing terms in an equation with no real solutions, such as x² − x + 1 = 0. He invoked the simplicity of the general rule as justification for introducing the multiple and complex roots, along with the fact that complex numbers provide solutions where otherwise none would exist.

37.1.2 Tschirnhaus Transformations

Every complex number has nth roots—exactly n of them except in the case of 0—that are also complex numbers. As a consequence, any formula for solving equations with complex coefficients that involves only the application of rational operations and root extractions starting with the coefficients will remain within the domain of complex numbers. This elementary fact led to the proposition stated by Girard, which we know as the fundamental theorem of algebra. Finding such a formula for equations of degree five and higher was to become a preoccupation of algebraists for the next two centuries.

By the year 1600, equations of degrees 2, 3, and 4 could all be solved, assuming that one could extract the cube root of a complex number (and that problem could not and cannot be reduced to purely algebraic operations on real numbers). The methods used to solve it—reducing the cubic to a quadratic equation in x³ and reducing the quartic to the resolvent cubic—suggest an inductive process in which the solution of an equation of degree n, say

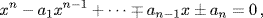
would be found by a substitution y = xⁿ⁻¹ − b₁xⁿ⁻² + ± b_n−2x 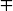b_n−1 with the coefficients b₁,. . ., b_n−1 chosen so that the original equation becomes yⁿ = C. Here we have n − 1 coefficients b_k at our disposal and n − 1 coefficients a₁,. . ., a_n−1 to be removed from the original equation. The program looks feasible. Something of the kind must have been the reasoning that led Ehrenfried Walther von Tschirnhaus (1652–1708) to the belief that he had discovered a general solution to all polynomial equations. In 1677 he wrote to Leibniz:

In Paris I received some letters from Mr. Oldenburg, but from lack of time have not yet been able to write back that I have found a new way of determining the irrational roots of all equations. . .The entire problem reduces to the following: We must be able to remove all the middle terms from any equation. When that is done, and as a result only a single power and a single known quantity remain, one need only extract the root.

Tschirnhaus claimed that the the middle terms (the a_k above) would be eliminated by a polynomial of the sort just discussed, provided that the b_k are suitably chosen. Such a change of variable is now called a Tschirnhaus transformation. If a Tschirnhaus transformation could be found for the general equation of degree n, and a formula existed for solving the general equation of degree n − 1, the two could be combined to generate a formula for solving the general equation of degree n. At the time, there was not even a Tschirnhaus transformation for the cubic equation. Tschirnhaus was to provide one.

He illustrated his transformation using the example x³ − qx − r = 0. Taking y = x² − ax − b, he noted that y satisfied the equation²

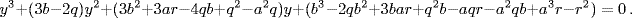
He eliminated the square term by choosing b = 2q/3, then removed the linear term by solving for a in the quadratic equation

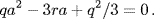
In this way, he had found at the very least a second solution of the general cubic equation, independent of the solution given by Cardano. And, what is more important, he had indicated a plausible way by which any equation might be solved. If it worked, it would prove that every polynomial equation could be solved using rational operations and root extractions, thereby proving at the same time that the complex numbers are algebraically closed. Unfortunately, detailed examination of the problem revealed difficulties that Tschirnhaus had apparently not noticed at the time of his letter to Leibniz.

When folding is used twice with the two polynomial equations p_n(x) = 0 and y = p_n−1(x), where p_n is of degree n and p_n−1 of degree n − 1, the polynomial that remains, just as in the case n = 3, contains a constant term and a linear term in x whose coefficients are linear functions of y. Those two terms would make it possible to express x as a fractional-linear function of y. Unfortunately, this polynomial also contains terms of degrees up to n − 2. Those terms can be removed by a suitable choice of parameters in p_n−1(x), but doing so requires fixing all but 2 of the coefficients. As a result, it is not in general possible to remove more than two of the coefficients in the resulting equation of degree n in this way. Only in the case of a cubic does that elimination produce a pure equation. The process may, however, work for a particular equation of higher degree. Leibniz was not convinced. He wrote to Tschirnhaus,

I do not believe that [your method] will be successful for equations of higher degree, except in special cases. I believe that I have a proof for this. [Kracht and Kreyszig, 1990, p. 27]

Tschirnhaus' method had intuitive plausibility: If there existed an algorithm for solving all equations, that algorithm should be a procedure like the Tschirnhaus transformation. Because the method does not work, the thought suggests itself that there may be equations that cannot be solved algebraically. The work of Tschirnhaus and Girard had produced two important insights into the general problem of polynomial equations: (1) The coefficients are symmetric functions of the roots; (2) solving the equation should be a matter of finding a sequence of operations that would eliminate coefficients until a pure equation yⁿ = C was obtained. Since the problem was still unresolved, still more new insights were needed.

To explain the most important of these new insights, let us consider what Girard's result means when applied to Cardano's solution of the cubic y³ + py = q. If the roots of this equation are r, s, and t, then p = st + tr + rs, q = rst, t = − r − s, since the coefficient of y² is zero. The sequence of operations implied by Cardano's formula is

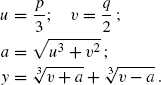
Girard's work implies that the quantity a, which is an irrational function of the coefficients p and q, is a rational function of the roots r, s, and t:

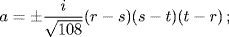
that is, it does not involve taking the square root of any expression containing a root.

37.1.3 Newton, Leibniz, and the Bernoullis

In the 1670s, Newton wrote a textbook of algebra called Arithmetica universalis, which was published in 1707, in which he stated more clearly and generally than Girard had done the relation between the coefficients and roots of a polynomial. Moreover, he showed that symmetric polynomials in the roots could be expressed as polynomials in the coefficients by giving a set of rules that are still known by his name.

Another impetus toward the fundamental theorem of algebra came from calculus. The well-known method known as partial fractions for integrating a quotient of two polynomials reduces all such problems to the purely algebraic problem of factoring the denominator. It is not immediately obvious that the denominator can be factored into linear and quadratic real factors; that is the content of the fundamental theorem of algebra. John Bernoulli asserted in a paper in the Acta eruditorum in 1702 that such a factoring was always possible, and therefore all rational functions could be integrated. Leibniz did not agree, arguing that the polynomial x⁴ + a², for example, could not be factored into quadratic factors over the reals. Here we see a great mathematician being misled by following a method. He recognized that the factorization had to be 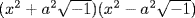and that the first factor should therefore be factored as 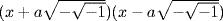and the second factor as 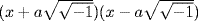, but he did not realize that these factors could be combined to yield 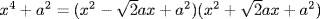. It was pointed out by Nicholas Bernoulli I (1687–1759) in the Acta eruditorum of 1719 (three years after the death of Leibniz) that this last factorization was a consequence of the identity x⁴ + a⁴ = (x² + a²)² − 2a²x².

37.2 Euler, D'Alembert, and Lagrange

The eighteenth century saw considerable progress in the understanding of equations in general and the procedures needed to solve them. Much of this new understanding came from the two men who dominated mathematical life in that century, Euler and Lagrange.

37.2.1 Euler

In his 1749 paper “Recherches sur les racines imaginaires des équations” (“Investigations into the imaginary roots of equations”), devoted to equations whose degree is a power of 2 and published in the memoirs of the Berlin Academy, Euler showed that when the coefficients of a polynomial are real, its roots occur in conjugate pairs, and therefore produce irreducible real quadratic factors of the form (x − a)² + b². In this paper, Euler argued that every polynomial of degree 2ⁿ with real coefficients can be factored as a product of two polynomials of degree 2ⁿ⁻¹ with real coefficients. In the course of the proof, Euler presented the germ of an idea that was to have profound consequences. In showing that a polynomial of degree 8 could be written as a product of two polynomials of degree 4, he assumed that the coefficient of x⁷ was made equal to zero by means of a linear substitution. The remaining polynomial x⁸ − ax⁶ + bx⁵ − cx⁴ − dx² + ex − f was then to be written as a product

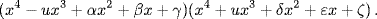
Euler noted that since u was the sum of four roots of the equation, it could assume (potentially) 70 values (the number of combinations of eight things taken four at a time), and its square would satisfy an equation of degree 35.

In the 1749 paper, Euler also conjectured that the roots of an equation of degree higher than 4 cannot be constructed by applying a finite number of algebraic operations to the coefficients. This was the first explicit statement of such a conjecture.

In his 1762 paper “De resolutione aequationum cuiusque gradus” (“On the solution of equations of any degree”), published in the Commentarii of the Petersburg Academy, Euler tried a different approach,³ assuming a solution of the form

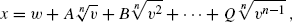
where is a real number and and the coefficients A,. . ., Q are to be found by a procedure resembling a Tschirnhaus transformation. This approach was useful for equations of degree 2ⁿ, but fell short of being a general solution of all polynomial equations.

37.2.2 D'Alembert

Euler's contemporary and correspondent d'Alembert tried to prove that all polynomials could be factored into linear and quadratic factors in order to prove that all rational functions could be integrated by partial fractions. In the course of his argument he assumed that any algebraic function could be expanded in a series of fractional powers of the independent variable. While Euler was convinced by this proof, he also wrote to d'Alembert to say that this assumption would be questioned (Bottazzini, 1986, pp. 15–18).

37.2.3 Lagrange

In 1770, Lagrange made a survey of the methods known up to his time for solving general equations. He devoted a great deal of space to a preliminary analysis of the cubic and quartic equations. In particular, he was intrigued by the fact that the resolvent equation, which he called the reduced equation (équation reduite), for the cubic was actually an equation of degree 6 that just happened to be quadratic in the third power of the unknown. He showed that if the roots of the cubic equation x³ + px = q being solved were a, b, and c, then a root of the resolvent would be

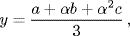
where α³ = 1, α ≠ 1. He argued that since the original equation was symmetric in a, b, and c, the resolvent would have to admit this y as a root, no matter how the letters a, b, and c were permuted. It therefore followed that the resolvent would in general have six different roots. (Note, however, that y³ assumes only two values under these permutations, and therefore satisfies it a quadratic equation whose coefficients are rational functions of p and q that can be computed by an algorithm.)

For the quartic equation with roots a, b, c, and d, he showed that the resolvent cubic equation would have a root

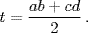
Since this expression could assume only three different values when the roots were permuted—namely, half of ab + cd, ac + bd, or ad + bc—it would have to satisfy an equation of degree three with coefficients expressible in terms of those of the original equation.

Proceeding to equations of fifth degree, Lagrange examined the only methods proposed up to that time, by Tschirnhaus and Euler–Bézout, and showed that the resolvent to be expected in all cases would be of degree 24. Pointing out that even Tschirnhaus, Euler, and Bézout themselves had not seriously attacked equations of degree five or higher, nor had anyone else tried to extend their methods, he said, “It is therefore greatly to be desired that one could estimate a priori the success that is to be expected in applying these methods to degrees higher than the fourth.” He then set out to provide proof that, in general, one could not expect the resolvent equation to reduce to lower degree than the original equation in such cases, at least using the methods mentioned.

To prove his point, Lagrange analyzed the method of Tschirnhaus from a more general point of view. For cubic and quartic equations, in which only two coefficients needed to be eliminated (the linear and quadratic terms in the cubic, the linear and cubic terms in the quartic), the substitution y = x² + ax + b would always work, since the elimination procedure resulted in linear and quadratic expressions in a and b in the coefficients that needed to be eliminated. Still, as Lagrange remarked, that meant two pairs of possible values (a, b) and hence really two cubic resolvents to be solved. The resolvent was therefore once again an equation of degree 6, which happened to be a quadratic polynomial in the cube of the variable. He noted what must be an ominous sign for those hoping to solve all algebraic equations by algebraic methods: The construction of the coefficients in the resolvent for an equation of degree n appeared to require solving n − 1 equations in n − 1 unknowns, of degrees 1, 2,. . ., n − 1, so that eliminating the variable x in these equations therefore led to an expression for x that was of degree (n − 1) ! in y, and hence to a resolvent equation of degree n ! in y.

Lagrange summed up his analysis as follows:

To apply, for example, the method of Tschirnhaus to the equation of degree 5, one must solve four equations in four unknowns, the first being of degree 1, the second of degree 2, and so on. Thus the final equation resulting from the elimination of three of these unknowns will in general be of degree 24. But apart from the immense amount of labor needed to derive this equation, it is clear that after finding it, one will be hardly better off than before, unless one can reduce it to an equation of degree less than 5; and if such a reduction is possible, it can only be by dint of further labor, even more extensive than before.

The technique of counting the number of different values the root of the resolvent will have when the roots of the original equation are permuted among themselves was an important clue in solving the problem of the quintic.

37.3 The Fundamental Theorem of Algebra and Solution by Radicals

The question of the theoretical existence of roots was settled on an intuitive level in the 1799 dissertation of Gauss. Gauss distinguished between the abstract existence of a root, which he proved, and an algebraic algorithm for finding it, the existence of which he doubted. He pointed out that attempts to prove the existence of a root and any possible algorithm for finding it must assume the possibility of extracting the nth root of a complex number. He also noted the opinion, first stated by Euler, that no algebraic algorithm existed for solving the general quintic.

The reason we say that the existence of roots was settled only on the intuitive level is that the proof of the fundamental theorem of algebra is as much topological as algebraic. The existence of real roots of an equation of odd degree with real coefficients seems obvious since a real polynomial of odd degree tends to oppositely signed infinities as the independent variable ranges from one infinity to the other. It thus follows by connectivity that it must assume a zero at some point. Gauss' proof of the existence of complex roots was similar. Much of what he was doing was new at the time, and he had to explain it in considerable detail. For that reason, he preferred to use only real-variable methods, so as not to raise any additional doubts with the use of complex numbers. In fact, he stated his purpose in that way: to prove that every polynomial with real coefficients has a complete factorization into linear and quadratic real polynomials. (It was noted above that d'Alembert had proposed a proof of this theorem, but Gauss found it defective, since it conflated an infimum with a minimum.)

The complex-variable background of the proof is obvious nowadays, and Gauss admitted that his lemmas were normally proved using complex numbers. The steps were as follows. First, considering the equation z^m + Az^m−1 + Bz^m−2 + + Kz² + Lz + M = 0, where all coefficients A,. . ., M were real numbers,⁴ taking z = r(cos ϕ + i sin ϕ) and using the relation z^m = r^m(cos mϕ + i sin mϕ), one can see that finding a root amounts to setting the real and imaginary parts equal to zero simultaneously, that is, finding r and ϕ such that

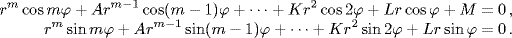
What remained was to show that there actually were points where the two curves intersected. For that purpose, Gauss divided both equations by r^m and argued that for large values of r the two functions must have zeros near the zeros of cos mϕ = 0 and sin mϕ = 0, respectively. That would mean that on a sufficiently large circle, each would have 2m zeros; and moreover, the zeros of the first curve, being near the points with polar angles (k + 1/2)π/m, must separate those of the second, which are near the points with polar angles kπ/m. Then, arguing that the portion of each curve inside the disk of radius r was connected, he said that it was obvious that one could not join all the pairs from one set and all the pairs from the other set using two curves that do not intersect.

Gauss was uneasy about the intuitive aspect of the proof. During his lifetime he gave several other proofs of the theorem that he regarded as more rigorous.

37.3.1 Ruffini

As it turned out, Gauss had no need to publish his own research on the quintic equation. In the very year in which he wrote his dissertation, the first claim of a proof that it is impossible to find a formula for solving all quintic equations by algebraic operations was made by the Italian physician Paolo Ruffini (1765–1822). Ruffini's proof was based on Lagrange's count of the number of values a function can assume when its variables are permuted.⁵ The principles of such a proof were gradually coming into focus. Newton's principle that every symmetric polynomial in the roots of a polynomial can be expressed as a function of its coefficients, proved by Edward Waring (1736–1798), was an important step, as was the idea of counting the number of different values a rational function of the roots can assume. To get the general proof, it was necessary to show that the root extractions performed in the course of a hypothetical solution would also be rational functions of the roots. That this is the case for quadratic and cubic equations is not difficult to see, since the quadratic formula for solving x² − (r₁ + r₂)x + r₁r₂ = 0 involves taking only one square root:

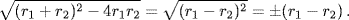
Similarly, the Cardano formula for solving y³ + (r₁r₂ + r₂r₃ + r₃r₁)y = r₁r₂r₃, where r₁ + r₂ + r₃ = 0, involves taking

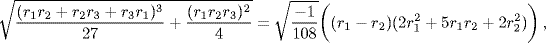
followed by extraction of the cube roots of the two numbers

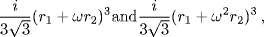
where 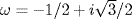is a complex cube root of 1. All of these radicals are consequently rational (but not symmetric) functions of the roots.

37.3.2 Cauchy

Although Ruffini's proof was not fully accepted by his contemporaries, it was endorsed many years later by Cauchy. In 1812, Cauchy wrote a paper entitled “Essai sur les fonctions symétriques” in which he proved the crucial fact that a polynomial in 5 variables that assumes fewer than 5 values when its variables are permuted assumes at most two values. In 1815 he published this result.

Cauchy gave credit to Lagrange, Alexandre Théophile Vandermonde (1735–1796), and Ruffini for earlier work in this area. Vandermonde, in particular, exhibited the Vandermonde determinant

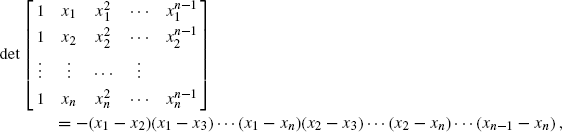
which assumes only two values, since interchanging two variables transposes the corresponding rows of the determinant and hence reverses the sign of the determinant.

37.3.3 Abel

Cauchy's work had a profound influence on two young geniuses whose lives were destined to be very short. The first of these, Abel, believed in 1821 that he had succeeded in solving the quintic equation. He sent his solution to the Danish mathematician Ferdinand Degen (1766–1825), who asked him to provide a worked-out example of a quintic equation that could be solved by Abel's method. While working through the details of an example, Abel realized his mistake. In 1824, he constructed an argument to show that such a solution was impossible and had the proof published privately. A formal version was published in the Journal für die reine und angewandte Mathematik in 1826. Abel was aware of Ruffini's work, and mentioned it in his argument. He attempted to fill in the gap in Ruffini's work with a proof that the intermediate radicals in any supposed solution by formula can be expressed as rational functions of the roots.

Abel's idea was that if some finite sequence of rational operations and root extractions applied to the coefficients produces a root of the equation

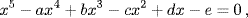
the final result must be expressible in the form

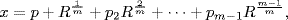
where p, p₂,. . ., p_m−1, and R are also formed by rational operations and root extractions applied to the coefficients, m is a prime number,⁶ and R^1/m is not expressible as a rational function of the coefficients a, b, c, d, e, p, p₂,. . ., p_m−1.⁷ By straightforward reasoning on a system of linear equations for the coefficients p_j, he was able to show that R is a symmetric function of the roots, and hence that R^1/m can assume the same m different values, no matter how the roots are permuted. Moreover, since there are 5 ! permutations of the roots and m is a prime, it followed that m = 2 or m = 5, the case m = 3 having been ruled out by Cauchy. The hypothesis that m = 5 led to an equation in which the left-hand side assumed only five values while the right-hand side assumed 120 values as the roots were permuted. Then the hypothesis m = 2 led to a similar equation in which one side assumed 120 values and the other only 10. Abel concluded that the hypothesis that there exists an algorithm for solving the equation was incorrect.

The standard version of the history of mathematics credits Abel with being “the” person who proved the impossibility of solving the quintic equation. But according to Ayoub (1980, p. 274), in 1832 the Prague Scientific Society declared the proofs of Ruffini and Abel unsatisfactory and offered a prize for a correct proof. The question was investigated by Hamilton in a report to the Royal Society in 1836 and published in the Transactions of the Royal Irish Academy in 1839. Hamilton's report was so heavily laden with subscripts and superscripts bearing primes that only the most dedicated reader would attempt to understand it, although Felix Klein (1884) was later to describe it as being “as lucid as it is voluminous.” The proof was described by the American number theorist and historian of mathematics Leonard Eugene Dickson as “a very complicated reconstruction of Abel's proof.” Hamilton regarded the problem of the solvability of the quintic as still open. He wrote:

[T]he opinions of mathematicians appear to be not yet entirely agreed respecting the possibility or impossibility of expressing a root as a function of the coefficients by any finite combination of radicals and rational functions.

The verdict of history has been that Abel's proof, suitably worded, is correct. Ruffini also had a sound method (see Ayoub, 1980), but needed to make certain subtle distinctions that were noticed only after the problem was better understood. By the end of the nineteenth century, Klein (1884) referred to “the proofs of Ruffini and Abel, by which it is established that a solution of the general equation of the fifth degree by extracting a finite number of roots is impossible.”

Besides his impossibility proof, Abel made positive contributions to the solution of equations. He generalized the work of Gauss on the cyclotomic (circle-splitting) equation xⁿ + xⁿ⁻¹ + + x + 1 = 0, which had led Gauss to the construction of the regular 17-sided polygon. Abel showed that if every root of an equation could be generated by applying a given rational function successively to a single (primitive) root, the equation could be solved by radicals. Any two permutations that leave this function invariant necessarily commute with each other. As a result, nowadays any group whose elements commute is called an abelian group.

37.3.4 Galois

More light was shed on the solution of equations by the work of Abel's contemporary Evariste Galois (1811–1832), a volatile young man who did not live to become even mature. As is well known, he died at the age of 20 in a duel fought with one of his fellow republicans.⁸

The concepts of group, ring, and field that make modern algebra the beautiful subject that it is grew out of the work of Abel and Galois, but neither of these two short-lived geniuses had a full picture of any of them. Where we now talk easily about algebraic and transcendental field extensions and regard the general equation of degree n over a field F as xⁿ + a₁xⁿ⁻¹ + + a_n−1x + a_n = 0, where each a_j is transcendental over F, Galois had to explain that the concept of a rational function was relative to what was given. For an equation with numerical coefficients, a rational function was simply a quotient of two polynomials with numerical coefficients, while if the equation had letters as coefficients, a rational function meant a quotient of two polynomials whose coefficients were rational functions of the coefficients of the equation. Even the concept of a group, which is associated with Galois, is not stated formally in any of his work. He does use the word group frequently in referring to a set of permutations of the roots of an equation, and he uses the properties that we associate with a group: the composition of permutations. However, it is clear from his language that what makes a set of permutations a group is that all of them have the same effect on certain rational functions of the roots. In particular, when what we now call a group is decomposed into cosets over a subgroup, Galois refers to the cosets as groups, since any two elements of a given coset have the same effect on the rational functions. He says that a group, in this sense, may begin with any permutation at all, since there is no need to specify any natural order of the roots.

Besides the shortness of their lives, Abel and Galois had another thing in common: neglect of their achievements by the Paris Academy of Sciences. Abel's most brilliant paper on general algebraic integrals (now called abelian integrals at the suggestion of Abel's rival Jacobi) was lost for over a decade until Jacobi, in 1841, insisted on its publication. As for Galois, he had been expelled from the École Normale because of his republican activities and had been in prison. He left a second paper among his effects, which was finally published in 1846. It had been written in January 1831, 17 months before his death, and it contained the following plaintive preface:

The attached paper is excerpted from a work that I had the honor to present to the Academy a year ago. Since this work was not understood, and doubt was cast on the propositions that it contains, I have had to settle for giving the general principles and only one application of my theorie in systematic order. I beg the referees at least to read these few pages with attention. [Picard, 1897, p. 33]

In a letter to a friend written the night before the duel in which he died, Galois showed that he had gone still further into this subject, making the distinction between proper and improper decompositions of the group of an equation, that is, the distinction we now make between normal and nonnormal subgroups.

The ideas of Abel and Galois were developed further by Laurent Wantzel (1814–1848) and Enrico Betti (1823–1892). Using reasoning about the roots of equations similar to that of Abel, Wantzel was able to prove (1837) that it is impossible to double the cube or trisect the angle using ruler and compass. More generally, he showed that any complex number that can be located using a straightedge and compass starting from the numbers 0 and 1 must satisfy an equation obtained by substituting one quadratic polynomial inside another a finite number n of times in such a way that the final polynomial of degree 2ⁿ is irreducible over the rational numbers. At the time, no one knew whether π could be the root of such a polynomial, and so the question of squaring the circle remained open for several more decades. Later, Wantzel gave a thorough classification of the roots of equations with rational coefficients, and in the process showed (1843, p. 125) that there is no algebraic algorithm that can be applied to the coefficients of a cubic equation with three real roots and yield a root without involving complex numbers at some intermediate stage. In 1845, he “cleaned up” Abel's proof that it is impossible to solve equations of degree five or higher in radicals (as Hamilton had already done nine years earlier). Nowadays, all of Wantzel's results are proved using Galois theory.

In 1852, Betti published a series of theorems elucidating the theory of solvability by radicals. In this way, group theory proved to be the key not only to the solvability of equations but to the full understanding of classical problems. When Ferdinand Lindemann (1852–1939) proved in 1881 that π is a transcendental number, it followed that no ruler-and-compass quadrature of the circle was possible.

The proof that the general quintic equation of degree 5 was not solvable by radicals naturally raised two questions: (1) How can the general quintic equation of degree 5 be solved? (2) Which particular quintic equations can be solved by radicals? These questions required some time to answer. Eventually, Charles Hermite⁹ (1822–1902) showed how to use elliptic integrals to solve the general quintic equation. The algebraic algorithm for solving a solvable quintic equation depends on the Galois group of the equation. Using modern computer algebra methods, mathematicians have produced a complete solution of this problem.¹⁰ An early summary of results in this direction was the famous book by Felix Klein on the icosahedron (1884). A study of the theory of solvability of equations of all degrees, with historical reference, can be found in the book of R. Bruce King (1996).

Problems and Questions

Mathematical Problems

37.1 Prove that if every polynomial with real coefficients has a zero in the complex numbers, then the same is true of every polynomial with complex coefficients. To get started, let p(z) = zⁿ + a₁zⁿ⁻¹ + + a_n−1z + a_n be a polynomial with complex coefficients a₁,. . ., a_n. Consider the polynomial q(z) of degree 2n given by 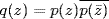, where the overline indicates complex conjugation. This polynomial has real coefficients, and so by hypothesis has a complex zero z₀.

37.2 You are familiar with the fact that for any two polynomials p(x) and q(x), there exist other polynomials a(x) and r(x) such that p(x) = a(x)q(x) + r(x), where r(x) is of lower degree than q(x). (This is the familiar long-division algorithm for polynomials.) The operation can be repeated using q(x) and r(x) in place of p(x) and q(x), eventually producing a remainder of maximal degree that divides both p(x) and q(x). This is the Euclidean algorithm discussed in Section 9.1 of Chapter 9. Because of this algorithm, it follows that every polynomial p(x) can be factored in only one way (up to constant multiples) as a product of irreducible polynomials, that is, polynomials that cannot be divided by any non-constant polynomial of lower degree. This is because an irreducible polynomial is prime in the sense that if it divides a product of two polynomials, it must divide one of the factors. Use this fact to prove that since p(x) is divisible by x − a if p(a) = 0, it follows that p(x) cannot have a number of roots that exceeds its degree.

37.3 Show that complex numbers of the form 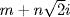, where m and n are integers can be added, subtracted, multiplied, and divided with a remainder, in the sense that given 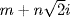and 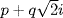, we can fi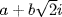nd and 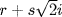such that

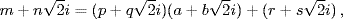
where 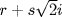is smaller than 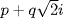in the sense that the norm 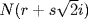, defined as r² + 2s², satisfies 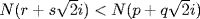. It follows from this result that an irreducible element of this form is prime in the sense of Problem 37.2, and hence that there is only one factorization (except for signs) for any number of this form. Does this result continue to hold if 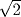is replaced by 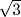? [Hint: The complex quotient

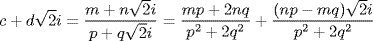
is not of the required form because c and d are not necessarily integers. However, there are integers a and b such that 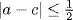and 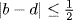. Write c = a + δ, d = b + ε, where 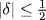and 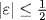, and show that the difference 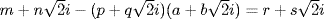satisfies the required inequality. For the second question, note that .]

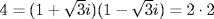Historical Questions

37.4 What advance in clarity concerning polynomial equations is due to Girard?

37.5 What was the conclusion of Lagrange's detailed analysis of the general algebraic equation?

37.6 How did the results of Abel and Galois bring a measure of completeness to the search for an algebraic formula to solve each equation?

Questions for Reflection

37.7 It is possible to define a multiplication on four-dimensional space by regarding the first coordinate as a real number and the last three as a vector. In other words, we can write formally

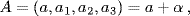
where a on the right stands for (a, 0, 0, 0) and α for (0, a₁, a₂, a₃). Addition of these quaternions, as they are called, is simple: A + B = (a + b) + (α + β), where of course B = b + β = (b, b₁, b₂, b₃). Multiplication is a little trickier, and we define A × B = (ab − α · β) + (aβ + bα + α × β), where α · β corresponds to the dot product (a₁b₁ + a₂b₂ + a₃b₃, 0, 0, 0), and α × β is the cross product (0, a₂b₃ − a₃b₂, a₃b₁ − a₁b₃, a₁b₂ − a₂b₁). It is not difficult to verify that 1 = (1, 0, 0, 0) has the property 1 × A = A × 1 = A for all quaternions A and that the quaternion conjugate 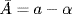satisfies 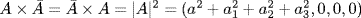, which is identified with the real number 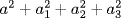. It follows that A⁻¹, defined to be 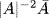is the inverse of A in the sense that A × A⁻¹ = A⁻¹ × A = 1 = (1, 0, 0, 0). Thus all the operations of arithmetic make sense on quaternions. One can add subtract, multiply, and divide. However, multiplying or dividing on the left is in general different from multiplying or dividing on the right. In general, the quaternions can be thought of as a number system containing a copy of the real numbers, infinitely many copies of the complex numbers, and a copy of ordinary three-dimensional vector space. That kind of generality causes a few restrictions in what can be said about quaternions.

Show that in quaternions the equation X² + r² = 0, where r is a positive real number, identified with the quaternion R = (r, 0, 0, 0), is satisfied precisely by the quaternions X = x + ξ such that x = 0, |ξ| = r, that is, by all the points on the sphere of radius r about the origin as center in three-dimensional space. In other words, in quaternions the square roots of negative real numbers are simply the nonzero vectors in three-dimensional space. Thus, even though quaternions act “almost” like the complex numbers, the fact that multiplication is not commutative makes a great difference when polynomial algebra is considered. In the quaternions, just as in the complex numbers, a linear equation can have only one solution. In contrast, while a quadratic equation can have only two solutions in the complex numbers, such an equation may have an uncountable infinity of solutions in the quaternions. Where does the proof that the number of roots does not exceed the degree of the equation, given above (Problem 37.2), break down? You can show nevertheless that if R = (r, 0, 0, 0) is a real solution of the equation P(X) = 0, then X − r does divide P(X), and so a quaternion polynomial cannot have a number of real solutions that exceeds its degree. This is because r commutes with every quaternion.

37.8 The results of Abel and Galois represent the outcome of many centuries of attempts to express the roots of a polynomial algebraically in terms of its coefficients. Meanwhile, computing the roots numerically from the coefficients—the approach followed in China and Japan—was a problem that had been solved centuries earlier. What are the advantages and disadvantages of each approach to the problem?

37.9 Consider the set of all real and complex numbers that can be located in the complex plane using only straight lines and circles (straightedge and compass) starting from two arbitrary points labeled 0 and 1. Denote this set E. We could call these “Euclidean numbers” or “constructible numbers” if we wished to invent a name for them. It is not difficult to show that if the complex numbers a, b, and c belong to E, then so do the roots of the quadratic equation ax² + bx + c = 0. Thus the Euclidean numbers are “quadratically closed.” Are they also algebraically closed, in the sense that the roots of every polynomial with coefficients in E also lie in E ? [Hint: Consider the problem of duplicating the cube. What number must be constructed to solve this problem, and what equation does it satisfy?]

Notes

1. In his textbook on analytic function theory (1959, p. 24), Einar Hille (1894–1980) wrote that “modern algebraists are inclined to deny both its algebraic and its fundamental character.” In the context of its time, the theorem was both algebraic and fundamental. The fact that the complex numbers are algebraically closed depends on the topological properties of the complex plane, especially the fact that it is a connected set. That connectedness would not exist if not for nonalgebraic (transcendental) numbers such as π and e. That is the meaning of Hille's statement that the algebraic closedness of the complex numbers is not an algebraic theorem.

2. This equation can be derived by Seki Kwa's method of tatami (folding), which makes it possible to express x as a fractional-linear function of y, and hence y as a fractional-linear function of x.

3. This approach was discovered independently by Etienne Bézout (1730–1783).

4. This restriction involves no loss of generality (see Problem 37.1 below).

5. An exposition of Ruffini's proof, clothed in modern terminology that Ruffini would not have recognized, can be found in the paper of Ayoub (1980).

6. Extracting any root is tantamount to the sequential extraction of prime roots. Hence every root extraction in the hypothetical process of solving the equation can be assumed to be the extraction of a prime root.

7. Abel incorporated the apparently missing coefficient p₁ into R here, since he saw no loss of generality in doing so. A decade later, William Rowan Hamilton pointed out that doing so might increase the index of the root that needed to be extracted, since p₁ might itself require the extraction of an mth root.

8. The word republican (républicain) is being used in its French sense, of course, not the American sense. It is the opposite of royaliste or légitimiste. (Cauchy was a légitimiste, who went into exile with the King after the 1848 revolution.) There are murky details about the duel, but it appears that the gun Galois used was not loaded, probably because he did not wish to kill a comrade-in-arms. It may be that the combatants had agreed to let fate determine the outcome and each picked up a weapon, not knowing which of the two guns was loaded. The cause of the duel is also not entirely clear. The notes that Galois left behind seem to imply that he felt it necessary to warn his friends about what he considered to be the wiles of a certain young woman by whom he felt betrayed, and they felt obliged to defend her honor against his remarks.

9. Hermite was also the first person to prove that e is a transcendental number, in 1858.

10. See the paper by D. S. Dummit “Solving solvable quintics,” in Mathematics of Computation, 57 (1991), No. 195, 387–401.