Chapter 45
Logic
The mathematization of logic has a prehistory that goes back to Leibniz (not published in his lifetime), but we shall focus on mostly the nineteenth-century work. After a brief discussion of the preceding period, we examine the period from 1847 to 1931. This period opens with the treatises of Boole and De Morgan and closes with Gödel's famous incompleteness theorem. Our discussion is not purely about logic in the earlier parts, since the earlier writers considered both logical and probabilistic reasoning.
45.1 From Algebra to Logic
Leibniz was one of the first to conceive the idea of creating an artificial language in which to express propositions. He compared formal logic to the lines drawn in geometry as guides to thought. If the language encoded thought accurately, thought could be analyzed in a purely mechanical manner:
“. . .when disagreements arise, there will be no more need for two philosophers to argue than for two accountants to do so. For it will suffice for them to take pen in hand, sit at their counting-boards, and say to each other, Let us calculate. [Gerhardt, 1971, Bd. 7, p. 200]
In another place he wrote:
Ordinary languages, though mostly helpful for the inferences of thought, are yet subject to countless ambiguities and cannot do the task of a calculus, which is to expose mistakes in inference. . .This remarkable advantage is afforded up to date only by the symbols of arithmeticians and algebraists, for whom inference consists only in the use of characters, and a mistake in thought and in the calculus is identical. [Quoted by Bochenski, 1961, p. 275]
Thus did Leibniz begin to extend the application of Euclidean formalism to all of philosophy. But it was not the Euclidean axioms that led him to do this. It was the spectacular development of algebra in his own time. This transition from the visual to the verbal, from intuition to language, was one of the prominent features of modern mathematics. It works quite well in arithmetic and other discrete systems and fairly well even with continuous systems such as the real numbers and the objects of geometry.
The ideal enunciated by Leibniz remains largely unfulfilled when it comes to settling philosophical disagreements. It reflects an oversimplified and optimistic view of human beings as basically rational creatures. This sort of optimism continued into the early nineteenth century, as exemplified by the Handbook of Political Fallacies by the philosopher Jeremy Bentham (1748–1832). But while the complex questions of the world of nature and society could not be mastered through logic alone, mathematics proved more amenable to the influence of logic. The influence, however, was bidirectional. In fact, there is a paradox, if one thinks of logic as being the rudder that steers mathematical arguments and keeps them from going astray. As the American philosopher/mathematician Charles Sanders Peirce (1839–1914) wrote in 1896, reviewing a book on logic:
It is a remarkable historical fact that there is a branch of science in which there has never been a prolonged dispute concerning the proper objects of that science. It is mathematics. . .Hence, we homely thinkers believe that, considering the immense amount of disputation there has always been concerning the doctrines of logic, and especially concerning those which would otherwise be applicable to settle disputes concerning the accuracy of reasonings in metaphysics, the safest way is to appeal for our logical principles to the science of mathematics. [Quoted in Bochenski, 1961, pp. 279–280]
Peirce seemed to believe that, far from sorting out the mathematicians, logicians should turn to them for guidance. But we may dispute his assertion that there has never been a prolonged dispute about the proper objects of mathematics. Zeno's paradoxes concern that very question. In Peirce's own day, Kronecker and Cantor were at opposite ends of a dispute about what is and is not proper mathematics, and that discussion continues, politely, down to the present day. See, for example, the book (1997) by Reuben Hersh (b. 1927).
Leibniz noted in the passage quoted above that algebra had the advantage of a precise symbolic language, which he held up as an ideal for clarity of communication. Algebra was one of the sources of mathematical logic. When De Morgan translated a French algebra textbook into English in 1828, he defined algebra as “the part of mathematics in which symbols are employed to abridge and generalize the reasonings which occur in questions relating to numbers.” Thus, for De Morgan at the time, the symbols represented numbers, but unspecified numbers, so that reasoning about them applied to any particular numbers. Algebra was a ship anchored in numbers, but it was about to slip its anchor.
Only two years later (in 1830) George Peacock (1791–1858) wrote a treatise on algebra in which he proposed that algebra be a purely symbolic science independent of any arithmetical interpretation. This step was a radical innovation at the time, considering that abstract groups, for example, were not to appear for several more decades. The assertion that the formula (a − b)(a + b) = a2 − b2 holds independently of any numerical values that replace a and b, for example, almost amounts to an axiomatic approach to mathematics. De Morgan's ideas on this subject matured during the 1830s, and at the end of the decade he wrote:
When we wish to give the idea of symbolical algebra. . .we ask, firstly, what symbols shall be used (without any reference to meaning); next, what shall be the laws under which such symbols are to be operated upon; the deduction of all subsequent consequences is again an application of common logic. Lastly, we explain the meanings which must be attached to the symbols, in order that they may have prototypes of which the assigned laws of operation are true. [Quoted by Richards, 1987, pp. 15–16]
This set of procedures is still the way in which mathematical logic operates, although the laws under which the symbols are to be operated on are now more abstract than De Morgan probably had in mind. To build a formal language, you first specify which sequences of symbols are to be considered “well-formed formulas,” that is, formulas capable of being true or false. The criterion for being well-formed must be purely formal, one that could in principle be used by a computer. Next, the sequences of well-formed formulas that are to be considered deductions are specified, again purely formally. The syntax of the language is specified by these two sets of rules, and the final piece of the construction, as De Morgan notes, is to specify its semantics, that is, the interpretation of its symbols and formulas. Here again, the modern world takes a more formal and abstract view of “interpretation” than De Morgan probably intended. For example, the semantics of propositional calculus consists of truth tables. After specifying the semantics, one can ask such questions as whether the language is consistent (incapable of proving a false proposition), complete (capable of proving all true propositions), or categorical (allowing only one interpretation, up to isomorphism).
In his 1847 treatise Formal Logic, De Morgan went further, arguing that “we have power to invent new meanings for all the forms of inference, in every way in which we have power to make new meanings of is and is not. . . .” This focus on the meaning of is was very much to the point. One of the disputes that Peirce overlooked in the quotation above is the question of what principles allow us to infer that an object “exists” in mathematics. We have seen this question in the eighteenth-century disagreement over what principles are allowed to define a function. In the case of symbolic algebra, where the symbols originally represented numbers, the existence question was still not settled to everyone's liking in the early nineteenth century. That is why Gauss stated the fundamental theorem of algebra in terms of real factorizations alone. Here De Morgan was declaring the right to create mathematical entities by fiat, subject to certain restrictions. That enigmatic “exists” is indispensable in first-order logic, where the negation of “For every x, P” is “For some x, not-P.” But what can “some” mean unless there actually exist objects x? This defect was to be remedied by De Morgan's friend George Boole (1815–1864).
In De Morgan's formal logic, this “exists” remains hidden: When he talks about a class X, it necessarily has members. Without this assumption, even his very first example is not a valid inference. He gives the following table by way of introduction to the symbolic logic that he is about to introduce:
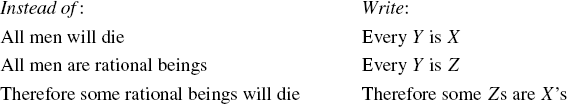
De Morgan's notation in this work was not the best, and very little of it has caught on. He used a parenthesis in roughly the same way as the modern notation for implication. For example, X) Y denoted the proposition “Every X is a Y.” Nowadays we would write X ⊃ Y (read “X horseshoe Y”) for “X implies Y.” (To add to the confusion, if x is the set of objects for which X is true and y the set for which Y is true, then X ⊃ Y actually means x ⊂ y.) The rest of his notation—X : Y for “Some X's are not Ys,” X . Y for “No X's are Ys,” and X Y for “Some X's are Ys”—is no longer used. For the negation of these properties he used lowercase letters, so that x denoted not-X. De Morgan introduced the useful “necessary” and “sufficient” language into implications: X) Y meant that Y was necessary for X and X was sufficient for Y. He gave a table of the relations between X or x and Y or y for the relations X) Y, X . Y, Y) X, and x . y. For example, given that X implies Y, he noted that this relation made Y necessary for X, y an impossible condition for X, y a sufficient condition for x, and Y a contingent (not necessary, not sufficient, not impossible) condition for x.
For compound propositions, he wrote PQ for conjunction (his word), meaning both P and Q are asserted, and P, Q for disjunction (again, his word), meaning either P or Q. He then stated what are still known as De Morgan's laws:
The contrary of PQ is p, q. Not both is either not one or not the other, or not either. Not either P nor Q (which we might denote by : P, Q or. P, Q) is logically ‘not P and not Q’ or pq: and this is then the contrary of P, Q.
45.2 Symbolic Calculus
An example of the new freedom in the interpretation of symbols actually occurred somewhat earlier than the time of De Morgan, in Lagrange's algebraic approach to analysis. Thinking of Taylor's theorem as
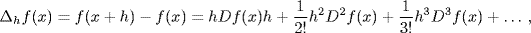
where Df(x) = f′ (x), and comparing with the Taylor series of the exponential function,
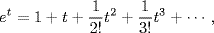
Lagrange arrived at the formal equation
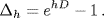
Although the equation is purely formal and should perhaps be thought of only as a convenient way of remembering Taylor's theorem, it does suggest a converse relation
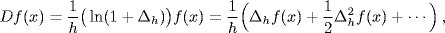
and this relation is literally true for polynomials f(x). The formal use of this symbolic calculus may have been merely suggestive, but as Grattan-Guinness remarks (2000, p. 19), “some people regarded these methods as legitimate in themselves, not requiring foundations from elsewhere.”
45.3 Boole's Mathematical Analysis of Logic
One such person was George Boole. In a frequently quoted passage from the introduction to his brief 1847 treatise The Mathematical Analysis of Logic, Boole wrote
[T]he validity of the processes of analysis does not depend upon the interpretation of the symbols which are employed but solely upon the laws of their combination. Every system of interpretation which does not affect the truth of the relations supposed is equally admissible, and it is thus that the same process may under one scheme of interpretation represent the solution of a question or the properties of number, under another that of a geometrical problem, and under a third that of optics.
Here Boole, like De Morgan, was arguing for the freedom to create abstract systems and attach an interpretation to them later. This step was still something of an innovation at the time. It was generally accepted, for example, that irrational and imaginary numbers had a meaning in geometry but not in arithmetic. One could not, or should not, simply define them into existence. Cayley raised this objection shortly after the appearance of Boole's treatise (see Grattan-Guinness, 2000, p. 41), asking whether it made any sense to write 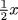 . Boole replied by comparing the question to the existence of
. Boole replied by comparing the question to the existence of 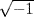 , which he said was “a symbol (i) which satisfies particular laws, and especially this: i2 = − 1.” In other words, when we are inventing a formal system, we are nearly omnipotent. Whatever we prescribe will hold for the system we define. If we want a square root of −1 to exist, it will exist (whatever “exist” may mean).
, which he said was “a symbol (i) which satisfies particular laws, and especially this: i2 = − 1.” In other words, when we are inventing a formal system, we are nearly omnipotent. Whatever we prescribe will hold for the system we define. If we want a square root of −1 to exist, it will exist (whatever “exist” may mean).
45.3.1 Logic and Classes
Although set theory had different roots on the Continent, we can see its basic concept—membership in a class—in Boole's work. Departing from De Morgan's notation, he denoted a generic member of a class by an uppercase X and used the lowercase x “operating on any subject,” as he said, to denote the class itself. Then xy was to denote the class “whose members are both X's and Ys.” This language rather blurs the distinction between a set, its members, and the properties that determine what the members are; but we should expect that clarity would take some time to achieve. The connection between logic and set theory is an intimate one and one that is easy to explain. But the kind of set theory that logic alone would have generated was different from the geometric set theory of Georg Cantor, which was intimately connected with the topology of the real line.
The influence of the mathematical theory of probability on logic is both extensive and interesting. The subtitle of De Morgan's Formal Logic is The Calculation of Inference, Necessary and Probable, and, as noted above, three chapters (some 50 pages) of Formal Logic are devoted to probability and induction. Probability deals with events, whereas logic deals with propositions. The connnection between the two was stated by Boole in his later treatise, An Investigation of the Laws of Thought, as follows:
[T]here is another form under which all questions in the theory of probabilities may be viewed; and this form consists in substituting for events the propositions which assert that those events have occurred, or will occur; and viewing the element of numerical probability as having reference to the truth of those propositions, not to the occurrence of the events.
Two events can combine in four different ways. Neither may occur, or E may occur but not F, or F may occur but not E, or E and F may both occur. If the events E and F are independent, the probability that both E and F occur is the product of their individual probabilities. If the two events cannot both occur, the probability that at least one occurs is the sum of their individual probabilities. More generally,
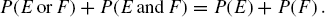
When these combinations of events are translated into logical terms, the result is a logical calculus.
The idea of probability 0 as indicating impossibility and probability 1 as indicating certainty must have had some influence on Boole's use of these symbols to denote “nothing” and “the universe.” He expressed the proposition “all X's are Y's,” for example, as xy = x or x(1 − y) = 0. Notice that 1 − y appears, not y − 1, which would have made no sense. Here 1 − y corresponds to the things that are not-y. From there, it is not far to thinking of 0 as false and 1 as true. The difference between probability and logic here is that the probability of an event may be any number between 0 and 1, while propositions are either true or false.1 These analogies were brought out fully in Boole's major work, to which we now turn.
45.4 Boole's Laws of Thought
Six years later, after much reflection on the symbolic logic that he and others had developed, Boole wrote an extended treatise, An Investigation of the Laws of Thought, which began by recapping what he had done earlier. The Laws of Thought began with a very general proposition that laid out the universe of symbols to be used. These were:
1st. Literal symbols, as x, y, &c., representing things as subjects of our conceptions.
2nd. Signs of operation, as +, −, ×, standing for those operations of the mind by which the conceptions of things are combined or resolved so as to form new conceptions involving the same elements.
3rd. The sign of identity, =.
And these symbols of Logic are in their use subject to definite laws, partly agreeing with and partly differing from the laws of the corresponding symbols in the science of Algebra.
Boole used + to represent disjunction (or) and juxtaposition, used in algebra for multiplication, to represent conjunction (and). The sign − was used to stand for “and not.” In his examples, he used + only when the properties were, as we would say, disjoint; and he used − only when the property subtracted was, as we would say, a subset of the property from which it was subtracted. He illustrated the equivalence of “European men and women” (where the adjective European is intended to apply to both nouns) with “European men and European women” as the equation z(x + y) = zx + zy. Similarly, to express the idea that the class of men who are non-Asiatic and white is the same as the class of white men who are not white Asiatic men, he wrote z(x − y) = zx − zy. He attached considerable importance to what he was later to call the index law, which expresses the fact that affirming a property twice conveys no more information than affirming it once. That is to say, xx = x, and he adopted the algebraic notation x2 for xx. This piece of algebraization led him, by analogy with the rules x0 = 0 and x1 = x, to conclude that “the respective interpretations of the symbols 0 and 1 in the system of Logic are Nothing and Universe.” From these considerations he deduced the principle of contradiction: x2 = x ⇒ x(1 − x) = 0, that is, no object can have a property and simultaneously not have that property.2
Boole was carried away by his algebraic analogies. Although he remained within the confines of his initial principles for a considerable distance, when he got to Chapter 5 he introduced the concept of developing a function. That is, for each algebraic expression f(x), no matter how complicated, finding an equivalent linear expression ax + b(1 − x), one that would have the same values as f(x) for x = 0 and x = 1. That expression would obviously be f(1)x + f(0)(1 − x). Boole gave a convoluted footnote to explain this simple fact by deriving it from Taylor's theorem and the idempotence property.
45.5 Jevons
Both De Morgan and Boole used the syllogism or modus ponens (inferring method) as the basis of logical inference, although De Morgan did warn against an overemphasis on it. William Stanley Jevons (1835–1882) formulated this law algebraically and adjoined to it a principle of indirect inference, which amounted to inference by exhaustive enumeration of cases. The possibility of doing the latter by sorting through slips of paper led him to the conclusion that this sorting could be done by machine. Since he had removed much of the mathematical notation used by Boole, he speculated that the mathematics could be entirely removed from it. He also took the additional step of suggesting, rather hesitantly, that mathematics was itself a branch of logic. According to Grattan-Guinness (2000, p. 59), this speculation apparently had no influence on the mathematical philosophers who ultimately developed its implications.
45.6 Philosophies of Mathematics
Other mathematicians besides Cantor were also considering ways of deriving mathematics logically from simplest principles. Gottlob Frege (1848–1925), a professor in Jena, who occasionally lectured on logic, attempted to establish logic on the basis of “concepts” and “relations” to which were attached the labels true or false. He was the first to establish a complete predicate calculus, and in 1884 wrote a treatise called Grundgesetze der Arithmetik (Principles of Arithmetic). Meanwhile in Italy, Giuseppe Peano (1858–1939) was axiomatizing the natural numbers. Peano took the successor relation as fundamental and based his construction of the natural numbers on this one relation and nine axioms, together with a symbolic logic that he had developed. The work of Cantor, Frege, and Peano attracted the notice of a young student at Cambridge, Bertrand Russell (1872–1969), who had written his thesis on the philosophy of Leibniz. Russell saw in this work confirmation that mathematics is merely a prolongation of formal logic. This view, that mathematics can be deduced from logic without any new axioms or rules of inference, is now called logicism. Gödel's work was partly a commentary on this program and the formalist program of Hilbert (discussed below) and can be interpreted as a counterargument to its basic thesis—that mathematics can be axiomatized. Logicism had encountered difficulties still earlier, however. Even the seemingly primitive notion of membership in a set turned out to require certain caveats.
45.6.1 Paradoxes
In 1897, Peano's assistant Cesare Burali-Forti (1861–1931), apparently unintentionally, revealed a flaw in the ordinal numbers.3 To state the problem in the clear light of hindsight, if two ordinal numbers satisfy x < y, then x  y, but y ∉ x. In that case, what are we to make of the set of all ordinal numbers? Call this set A. Like any other ordinal number, it has a successor A + 1 and A
y, but y ∉ x. In that case, what are we to make of the set of all ordinal numbers? Call this set A. Like any other ordinal number, it has a successor A + 1 and A  A + 1. But since A + 1 is an ordinal number, we must also have A + 1
A + 1. But since A + 1 is an ordinal number, we must also have A + 1  A, and hence A < A + 1 and A + 1 < A. This was the first paradox of uncritical set theory, but others were to follow.
A, and hence A < A + 1 and A + 1 < A. This was the first paradox of uncritical set theory, but others were to follow.
The most famous paradox of set theory arose in connection with cardinal numbers rather than ordinal numbers. Cantor had defined equality between cardinal numbers as the existence of a one-to-one correspondence between sets representing the cardinal numbers. Set B has larger cardinality than set A if there is no function f : A → B that is “onto,” that is, such that every element of B is f(x) for some x  A. Cantor showed that the set of all subsets of A, which we denote 2A, is always of larger cardinality than A, so that there can be no largest cardinal number. If f : A → 2A, the set C = {t
A. Cantor showed that the set of all subsets of A, which we denote 2A, is always of larger cardinality than A, so that there can be no largest cardinal number. If f : A → 2A, the set C = {t  A : t ∉ f(t)} is a subset of A, hence an element of 2A, and it cannot be f(x) for any x
A : t ∉ f(t)} is a subset of A, hence an element of 2A, and it cannot be f(x) for any x  A. To see why, assume the opposite, that is, C = f(x) for some x. Then either x
A. To see why, assume the opposite, that is, C = f(x) for some x. Then either x  C or x ∉ C. If x
C or x ∉ C. If x  C, then x
C, then x  f(x) and so by definition of C, x ∉ C. On the other hand, if x ∉ C, then x ∉ f(x), and again by definition of C, x
f(x) and so by definition of C, x ∉ C. On the other hand, if x ∉ C, then x ∉ f(x), and again by definition of C, x  C. Since the whole paradox results from the assumption that C = f(x) for some x, it follows that no such x exists, that is, the mapping f is not “onto.” This argument was at first disputed by Russell, who wrote in an essay entitled “Recent work in the philosophy of mathematics” (1901) that “the master has been guilty of a very subtle fallacy.” Russell thought that there was a largest set, the set of all sets. In a later reprint of the article he added a footnote explaining that Cantor was right.4 Russell's first attempt at a systematic exposition of mathematics as he thought it ought to be was his 1903 work Principles of Mathematics. According to Grattan-Guinness (2000, p. 311), Russell removed his objection to Cantor's proof and published his paradox in this work, but kept the manuscript of an earlier version, made before he was able to work out where the difficulty lay.
C. Since the whole paradox results from the assumption that C = f(x) for some x, it follows that no such x exists, that is, the mapping f is not “onto.” This argument was at first disputed by Russell, who wrote in an essay entitled “Recent work in the philosophy of mathematics” (1901) that “the master has been guilty of a very subtle fallacy.” Russell thought that there was a largest set, the set of all sets. In a later reprint of the article he added a footnote explaining that Cantor was right.4 Russell's first attempt at a systematic exposition of mathematics as he thought it ought to be was his 1903 work Principles of Mathematics. According to Grattan-Guinness (2000, p. 311), Russell removed his objection to Cantor's proof and published his paradox in this work, but kept the manuscript of an earlier version, made before he was able to work out where the difficulty lay.
To explain Russell's mistake (as Russell later explained it to himself), consider the set of all sets. We must, by its definition, believe it to be equal to the set of all its subsets. Therefore the mapping f(E) = E should have the property that Cantor says no mapping can have. Now if we apply Cantor's argument to this mapping, we are led to consider S = {E : E ∉ E}. By definition of the mapping f we should have f(S) = S, and so, just as in the case of Cantor's argument, we ask if S  S. Either way, we are led to a contradiction. This result is known as Russell's paradox.
S. Either way, we are led to a contradiction. This result is known as Russell's paradox.
After Russell had straightened out the paradox with a theory of types, he collaborated with his teacher Alfred North Whitehead (1861–1947) on a monumental derivation of mathematics from logic, published in 1910 as Principia mathematica.
45.6.2 Formalism
A different view of the foundations of mathematics was advanced by Hilbert, who was interested in the problem of axiomatization (the axiomatization of probability theory was the sixth of his famous 23 problems) and particularly interested in preserving as much as possible of the freedom to reason that Cantor had provided while avoiding paradoxes. The essence of this position, now known as formalism, is the idea stated by De Morgan and Boole that the legal manipulation of the symbols of mathematics and their interpretation are separate issues. Hilbert is famously quoted as having claimed that the words point, line, and plane should be replaceable by table, chair, and beer mug when a theorem is stated. Grattan-Guinness (2000, p. 208) notes that Hilbert may not have intended this statement in quite the way it is generally perceived and may not have thought the matter through at the time. He also notes (p. 471) that Hilbert never used the name formalism. Characteristic of the formalist view is the assumption that any mathematical object whatever may be defined, provided only that the definition does not lead to a contradiction. Cantor was a formalist in this sense (Grattan-Guinness, 2000, p. 119). In the formalist view, mathematics is the study of formal systems, but the rules governing those systems must be stated with some care. Formalism detaches the symbols and formulas of mathematics from the meanings attached to them in applications, making a distinction between syntax and semantics.
Hilbert had been interested in logical questions in the 1890s and early 1900s, but his work on formal languages such as propositional calculus dates from 1917. In 1922, when the intuitionists (discussed below) were publishing their criticism of mathematical methodologies, he formulated his own version of mathematical logic. In it, he introduced the concept of metamathematics, the study whose subject matter is the structure of a mathematical system.5 To avoid infinity in creating a formal language while preserving sufficient generality, Hilbert resorted to a “finitistic” device called a schema. Certain basic formulas are declared to be legitimate by fiat. Then a few rules are adopted, such as the rule that if A and B are legitimate formulas, so is [A ⇒ B]. This way of defining legitimate (well-formed) formulas makes it possible to determine in a finite number of steps whether or not a formula is well formed. It replaces the synthetic constructivist approach with an analytic approach (which can be reversed, once the analysis is finished, to synthesize a given well-formed formula from primitive elements).
The formalist approach makes a distinction between statements of arithmetic and statements about arithmetic. For example, the assertion that there are no positive integers x, y, z such that x3 + y3 = z3 is a statement of arithmetic. The assertion that this statement can be proved from the axioms of arithmetic is a statement about arithmetic. The metalanguage, in which statements are made about arithmetic, contains all the meaning to be assigned to the propositions of arithmetic. In particular, it becomes possible to distinguish between what is true (that is, what can be known to be true from the metalanguage) and what is provable (what can be deduced within the object language). Two questions thus arise in the metalanguage: (1) Is every deducible proposition true? (the problem of consistency); (2) Is every true proposition deducible? (the problem of completeness). As we shall see below, Gödel showed that the answer, for first-order recursive arithmetic and more generally for systems of that type, is very pessimistic. This language is not complete and is incapable of proving its own consistency.
45.6.3 Intuitionism
The most cautious approach to the foundations of mathematics, known as intuitionism, was championed by the Dutch mathematician Luitzen Egbertus Jan Brouwer (1881–1966). Brouwer was one of the most mystical of mathematicians, and his mysticism crept into his early work. He even published a pamphlet in 1905, claiming that true happiness came from the inner world and that contact with the outer world brought pain (Franchella, 1995, p. 305). In his dissertation at the University of Amsterdam in 1907, he criticized the logicism of Russell and Zermelo's axiom of choice. Although he was willing to grant the validity of constructing each particular countable ordinal number, he questioned whether one could meaningfully form the set of all countable ordinals.6 In a series of articles published from 1918 to 1928, Brouwer laid down the principles of intuitionism. These principles include the rejection not only of the axiom of choice beyond the countable case, but also of proof by contradiction. That is, the implication “A implies not-(not-A)” is accepted, but not its converse, “Not-(not-A) implies A.”
A specimen of Brouwer's philosophy may give some idea of the general trend of his thought. In lectures delivered at Cambridge University in 1946 (van Dalen, 1981), he defined a fleeing property7 to be a property f such that, for any given positive integer n it is possible to determine (via an algorithm) whether or not n has the property f, yet there is no known way of calculating any number possessing property f, and no known way of proving that no number has this property (van Dalen, 1981, pp. 6–7). As an example (not Brouwer's) let us take the property f for an integer n to mean that n is an odd perfect integer.
Brouwer recognized that the quality of being fleeing is not intrinsic to a property of the integers. It depends both on the definition of the property and on human history, and a property that is fleeing at one moment may cease to be fleeing at a later moment. For example, a positive integer that was a fifth power and simultaneously the sum of four other fifth powers was not known until the mid-twentieth century. These two conditions constituted a fleeing property until that time. They no longer do, since it is known that 275 + 845 + 1105 + 1335 = 1445. Proceeding from this definition, Brouwer defined the critical number κf for a fleeing property to be the smallest number having that property. (This is a number that is unknowable in principle as long as the property remains fleeing. If anyone ever produces even one example of a number with the property, it ceases to be fleeing.) He then further separates the positive integers into “up-numbers” of f, which are those at least as large as κf, and “down-numbers,” which are those that are smaller than κf. By the first part of the definition of a fleeing property, one can presumably establish that some initial segment of the positive integers consists of down-numbers. Brouwer then defines aν = 2−ν if ν is a down-number and aν = 2−κf if ν is an up-number. Finally, he defines the number sf to be the limit of aν as ν→ ∞. According to Brouwer, this example refutes the principle that one of p or not-p must be true. For, he says,
. . . neither is [sf] equal to zero nor is it different from zero and, although its irrationality is absurd, it is not a rational number.
For a person accustomed to ordinary logic, this last statement is extraordinary. Brouwer appears to be conflating what is known with what is true, asserting, like the baseball umpire who says “They aren't anything until I call them,” that this number does not have any properties until we know what those properties are. By ordinary logic, it is far from obvious that κf is defined. Indeed, in order to know what it is, we would have to annihilate it, since presumably κf is defined only while the property f is fleeing, and it ceases to be that once we know an integer that has property f. One is very much inclined to object that Brouwer has not really defined anything corresponding to the symbol κf, since the possibility exists that there are no numbers at all having property f, hence no smallest number with that property, and Brouwer has made no definition for κf in that case. In any case, the reader can see why intuitionism has not attracted a large number of adherents among mathematicians.
Intuitionists reject any proof whose implementation leaves choices to be made by the reader. Thus it is not enough in an intuitionist proof to say that objects of a certain kind exist. One must choose such an object and use it for the remainder of the proof. This extreme caution has rather drastic consequences. For example, the function f(x) defined in ordinary language as
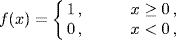
is not considered to be defined by the intuitionists, since there are ways of defining numbers x that do not make it possible to determine whether the number is negative or positive. For example, is the number (− 1)n, where n is the trillionth decimal digit of π, positive or negative? This restrictedness has certain advantages, however. The objects that are acceptable to the intuitionists tend to have pleasant properties. For example, every rational-valued function of a rational variable is continuous.
The intuitionist rejection of proof by contradiction needs to be looked at in more detail. Proof by contradiction was always used somewhat reluctantly by mathematicians, since such proofs seldom give insight into the structures being studied. For example, the modern proof that there are infinitely many primes proceeds by assuming that the set of prime numbers is a finite set P = {p1, p2,. . ., pn} and showing that in this case the number 1 + p1  pn must either itself be a prime number or be divisible by a prime different from p1,. . ., pn, which contradicts the original assumption that p1,. . ., pn formed the entire set of prime numbers.
pn must either itself be a prime number or be divisible by a prime different from p1,. . ., pn, which contradicts the original assumption that p1,. . ., pn formed the entire set of prime numbers.
The appearance of starting with a false assumption and deriving a contradiction can be avoided here by stating the theorem as follows: If there exists a set of n primes p1,. . ., pn, there exists a set of n + 1 primes. The proof is exactly as before. Nevertheless, the proof is still not intuitionistically valid, since there is no way of saying whether or not 1 + p1  pn is prime. In intuitionistic logic, if “p or q” is a theorem, then either p is a theorem or q is a theorem.
pn is prime. In intuitionistic logic, if “p or q” is a theorem, then either p is a theorem or q is a theorem.
In 1928 and 1929, a quarter-century after the debate over Zermelo's axiom of choice, there was debate about intuitionism in the bulletin of the Belgian Royal Academy of Sciences. Two Belgian mathematicians, M. Barzin (dates unknown) and A. Errera (dates unknown), had argued that Brouwer's logic amounted to a three-valued logic, since a statement could be true, false, or undecidable. The opposite point of view was defended by two Russian mathematicians, Aleksandr Yakovlevich Khinchin (1894–1959) and Valerii Ivanovich Glivenko (1897–1940). Barzin and Errera had suggested that to avoid three-valued logic, intuitionists ought to adopt as an axiom that if p implies “q or r,” then either p implies q or p implies r, and also that if “p or q” implies r, then p implies r and q implies r. Starting from these principles of Barzin and Errera and the trivial axiom “p or not-p” implies “p or not-p,” Khinchin deduced that p implies not-p and not-p implies p, thus reducing the suggestions of Barzin and Errera to nonsense. Glivenko took only a little longer to show that, in fact, Brouwer's logic was not three-valued. He proved that the statement “p or not-p is false” is false in Brouwer's logic, and ultimately derived the theorem that the statement “p is neither true nor false” is false (see Novosyolov, 2000).
A more “intuitive” objection to intuitionism is that intuition by its nature cannot be codified as a set of rules. In adopting such rules, the intuitionists were not being intuitionistic in the ordinary sense of the word. In any case, intuitionist mathematics is obviously going to be somewhat sparser in results than mathematics constructed on more liberal principles. That may be why it has attracted only a limited group of adherents.
45.6.4 Mathematical Practice
The paradoxes of naive set theory (such as Russell's paradox) were found to be avoidable if the word class is used loosely, as Cantor had previously used the word set, but the word set is restricted to mean only a class that is a member of some other class. (Classes that are not sets are called proper classes.) Then to belong to a class A, a class B must not only fulfill the requirements of the definition of the class A but must also be known in advance to belong to some (possibly different) class.
This approach avoids Russell's paradox. The class C = {x : x ∉ x} is a class; its elements are those classes that belong to some class and are not elements of themselves. If we now ask the question that led to Russell's paradox—Is C a member of itself?—we do not reach a contradiction. If we assume C  C, then we conclude that C ∉ C, so that this assumption is not tenable. However, the opposite assumption, that C ∉ C, is acceptable. It no longer leads to the conclusion that C
C, then we conclude that C ∉ C, so that this assumption is not tenable. However, the opposite assumption, that C ∉ C, is acceptable. It no longer leads to the conclusion that C  C. For an object x to belong to C, it no longer suffices that x ∉ x; it must also be true that x
C. For an object x to belong to C, it no longer suffices that x ∉ x; it must also be true that x  A for some class A, an assumption not made for the case when x is C. A complete set of axioms for set theory avoiding all known paradoxes was worked out by Paul Bernays (1888–1977) and Adolf Fraenkel (1891–1965). It forms part of the basic education of mathematicians today. It is generally accepted because mathematics can be deduced from it. However, it is very far from being a clear, concise, and therefore obviously consistent, foundation for mathematics. The axioms of set theory are extremely complicated and nonintuitive and are far less obvious than many things deduced from them. Moreover, their consistency is not only not obvious, it is even unprovable. In fact, one textbook of set theory, Introduction to Set Theory, by J. Donald Monk (McGraw-Hill, New York, 1969, p. 22), asserts regarding these axioms: “Naturally no inconsistency has been found, and we have faith that the axioms are, in fact, consistent”! (Emphasis added.)
A for some class A, an assumption not made for the case when x is C. A complete set of axioms for set theory avoiding all known paradoxes was worked out by Paul Bernays (1888–1977) and Adolf Fraenkel (1891–1965). It forms part of the basic education of mathematicians today. It is generally accepted because mathematics can be deduced from it. However, it is very far from being a clear, concise, and therefore obviously consistent, foundation for mathematics. The axioms of set theory are extremely complicated and nonintuitive and are far less obvious than many things deduced from them. Moreover, their consistency is not only not obvious, it is even unprovable. In fact, one textbook of set theory, Introduction to Set Theory, by J. Donald Monk (McGraw-Hill, New York, 1969, p. 22), asserts regarding these axioms: “Naturally no inconsistency has been found, and we have faith that the axioms are, in fact, consistent”! (Emphasis added.)
45.7 Doubts about Formalized Mathematics: Gödel's Theorems
The powerful and counterintuitive results obtained from the axiom of choice naturally led to doubts about the consistency of set theory. Since it was being inserted under the rest of mathematics as a foundation, the consistency question became an important one. A related question was that of completeness. Could one provide a foundation for mathematics, that is, a set of basic objects and rules of proof, that would allow any meaningful proposition to be proved true or false? The two desirable qualities of consistency and completeness are in the abstract opposed to each other, just as avoiding disasters and avoiding false alarms are opposing goals.
The most influential figure in mathematical logic during the twentieth century was Kurt Gödel (1906–1978). The problems connected with consistency and completeness of arithmetic, the axiom of choice, and many others all received a fully satisfying treatment at his hands that settled many old questions and opened up new areas of investigation. In 1931, he astounded the mathematical world by producing a proof that any consistent formal language in which arithmetic can be encoded is necessarily incomplete, that is, contains statements that are true according to its metalanguage but not deducible within the language itself. The intuitive idea behind the proof is a simple one, based on the following statement:
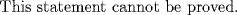
Assuming that this statement has a meaning—that is, its context is properly restricted so that “proved” has a definite meaning—we can ask whether it is true. The answer must be positive if the system in which it is made is consistent. For if this statement is false, by its own content, it can be proved; and in a consistent deductive system, a false statement cannot be proved. Hence we agree that the statement is true, but, again by its own content, it cannot be proved.
The example just given is really nonsensical, since we have not stated the axioms and rules of inference that provide the context in which the statement is made. The word “proved” that it contains is not really defined. Gödel, however, took an accepted formalization of the axioms and rules of inference for arithmetic and showed that the metalanguage of arithmetic could be encoded within arithmetic. In particular each formula can be numbered uniquely, and the statement that formula n is (or is not) deducible from those rules can itself be coded as a well-formed formula of arithmetic. Then, when n is chosen so that the statement “Formula number n cannot be proved” happens to be formula n, we have exactly the situation just described. Gödel showed how to construct such an n. Thus, if Gödel's version of arithmetic is consistent, it contains statements that are formally undecidable. They are true (based on the metalanguage) but not deducible. This is Gödel's first incompleteness theorem. His second incompleteness theorem is even more interesting: The assertion that arithmetic is consistent is one of the formally undecidable statements.8 If the formalized version of arithmetic that Gödel considered is consistent, it is incapable of proving itself so. It is doubtful, however, that one could truly formalize every kind of argument that a rational person might produce. For that reason, care should be exercised in drawing inferences from Gödel's work to the actual practice of mathematics.
Problems and Questions
Mathematical Problems
45.1. Suppose that the only allowable way of forming new formulas from old ones is to connect them by an implication sign; that is, given that A and B are well formed, [A ⇒ B] is well formed, and conversely, if A and B are not both well formed, then neither is [A ⇒ B]. Suppose also that the only basic well-formed formulas are p, q, and r. Show that
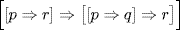
is well formed but
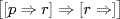
is not. Describe a general algorithm for determining whether a finite sequence of symbols is well formed.
45.2. Consider the following theorem. There exists an irrational number that becomes rational when raised to an irrational power. Proof: Consider the number 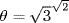 . If this number is rational, we have an example of such a number. If it is irrational, the equation
. If this number is rational, we have an example of such a number. If it is irrational, the equation 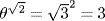 provides an example of such a number. Is this proof intuitionistically valid?
provides an example of such a number. Is this proof intuitionistically valid?
45.3. Prove that C = {x : x ∉ x} is a proper class, not a set, that is, it is not an element of any class. (The assumption that it is an element of some class means it is a set, and then Russell's paradox results.)
Historical Questions
45.4. How did algebra influence the interaction of mathematics and logic starting in the nineteenth century?
45.5. What was Charles Sanders Peirce's view of the relation between mathematics and logic?
45.6. What are the three major twentieth-century views of the philosophy of mathematics, and how do they differ from one another?
Questions for Reflection
45.7. Are there true but unknowable propositions in everyday life? Suppose that your class meets on Monday, Wednesday, and Friday. Suppose also that your instructor announces one Friday afternoon that you will be given a surprise exam at one of the regular class meetings the following week. One of the brighter students then reasons as follows. The exam will not be given on Friday, since if it were, having been told that it would be one of the three days, and not having had it on Monday or Wednesday, we would know on Thursday that it was to be given on Friday, and so it wouldn't be a surprise. Therefore it will be given on Monday or Wednesday. But then, since we know that it can't be given on Friday, it also can't be given on Wednesday. For if it were, we would know on Tuesday that it was to be given on Wednesday, and again it wouldn't be a surprise. Therefore it must be given on Monday, we know that now, and therefore it isn't a surprise. Hence it is impossible to give a surprise examination next week.
Obviously something is wrong with the student's reasoning, since the instructor can certainly give a surprise exam. Most students, when trying to explain what is wrong with the reasoning, are willing to accept the first step. That is, they grant that it is impossible to give a surprise exam on the last day of an assigned window of days. Yet they balk at drawing the conclusion that this argument implies that the originally next-to-last day must thereby become the last day. Notice that, if the professor had said nothing to the students, it would be possible to give a surprise exam on the last day of the window, since the students would have no way of knowing that there was any such window. The conclusion that the exam cannot be given on Friday therefore does not follow from assuming a surprise exam within a limited window alone, but rather from these assumptions supplemented by the following proposition: The students know that the exam is to be a surprise and they know the window in which it is to be given.
This fact is apparent if you examine the student's reasoning, which is full of statements about what the students would know. Can they truly know a statement (even a true statement) if it leads them to a contradiction?
Explain the paradox in your own words, deciding whether the exam would be a surprise if given on Friday. Can the paradox be avoided by saying that the conditions under which the exam is promised are true but the students cannot know that they are true?
How does this puzzle relate to Gödel's incompleteness result?
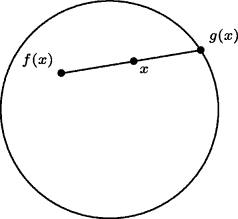
45.8. Brouwer, the leader of the intuitionist school of mathematicians, is also known for major theorems in topology, including the invariance of geometric dimension under homeomorphisms. One of his results is the Brouwer fixed-point theorem, which asserts that for any continuous mapping f of a closed disk into itself there is a point x such that x = f(x). To prove this theorem, suppose there is a continuous mapping f for which f(x) ≠ x at every point x. Construct a continuous mapping g by drawing a line from f(x) to x and extending it to the point g(x) at which it meets the boundary circle (see Fig. 45.1). Then g(x) maps the disk continuously onto its boundary circle and leaves each point of the boundary circle fixed. Such a continuous mapping is intuitively impossible (imagine stretching the entire head of a drum onto the rim without moving any point already on the rim and without tearing the head) and can be shown rigorously to be impossible (the disk and the circle have different homotopy groups). How can you explain the fact that the champion of intuitionism produced theorems that are not intuitionistically valid?
Figure 45.1 The Brouwer fixed-point theorem.
45.9. Suppose that you prove a theorem by assuming that it is false and deriving a contradiction. What you have then proved is that either the axioms you started with are inconsistent or the assumption that the theorem is false is itself false. Why should you conclude the latter rather than the former? Is this why some mathematicians have claimed that the practice of mathematics requires faith?
Notes
1. Classical set theory deals with propositions of the form x  E, which are either true or false: Either x belongs to E, or it does not, and there is no other possibility. The recently created fuzzy set theory restores the analogy with probability, allowing an element to belong partially to a given class and expressing the degree of membership by a function ϕ(x) whose values are between 0 and 1. Thus, for example, whether a woman is pregnant or not is a classical set-theory question; whether she is tall or not is a fuzzy set-theory question. Fuzzy-set theorists point out that their subject is not subsumed by probability, since it deals with the properties of individuals, not those of large sets.
E, which are either true or false: Either x belongs to E, or it does not, and there is no other possibility. The recently created fuzzy set theory restores the analogy with probability, allowing an element to belong partially to a given class and expressing the degree of membership by a function ϕ(x) whose values are between 0 and 1. Thus, for example, whether a woman is pregnant or not is a classical set-theory question; whether she is tall or not is a fuzzy set-theory question. Fuzzy-set theorists point out that their subject is not subsumed by probability, since it deals with the properties of individuals, not those of large sets.
2. Nowadays, a ring in which every element is idempotent—that is, the law x2 = x holds—is called a Boolean ring. It is an interesting exercise to show that such a ring is always commutative and of characteristic 2; that is, x + x = 0 for all x. The subsets of a given set form a Boolean ring when addition is interpreted as symmetric difference; that is, A + B means “either A or B but not both.”
3. Moore (1982, p. 59) notes that Burali-Forti himself did not see any paradox and (p. 53) that the difficulty was known earlier to Cantor.
4. Moore (1982, p. 89) points out that Zermelo had discovered Russell's paradox two years before Russell discovered it and had written to Hilbert about it. Zermelo, however, did not consider it a very troubling paradox. To him it meant only that no set should contain all of its subsets as elements.
5. This distinction had been introduced by L. E. J. Brouwer in his 1907 thesis, but not given a name and never developed (see Grattan-Guinness, 2000, p. 481).
6. This objection seems strange at first, but the question of whether an effectively defined set must have effectively defined members is not at all trivial.
7. Had English been his native language, Brouwer would probably have called this a fugitive property. In contrast to the English written by most of his compatriots, which is polished and elegant, Brouwer's was barbarous. He coined such atrocities as noncontradictority and supposable.
8. Detlefsen (2001) has analyzed the meaning of proving consistency in great detail and concluded that the generally held view of this theorem—that the consistency of a “sufficiently rich” theory cannot be proved by a “finitary” theory—is incorrect.