

God gave us the darkness so we could see the stars.
—Johnny Cash, in “Farmers Almanac”
Seven A.M. With unnerving suddenness, the alarm from your electronic clock wakes you from the depths of a pleasant dream. “Damn,” you whisper. A romantic image fades like an angel drifting off into distant clouds. Why does the alarm have to go off now?
Even though you’ve had the clock since high school, you’ve never become accustomed to its shrill beeping. Within seconds you silence it by reaching for a button on its surface. Your finger encounters the old, familiar scratch from the last time you threw the clock across your bedroom. Now the scratch allows you to guide your finger to the button bringing blessed silence.
You slowly sit up in bed, push aside your blankets, and turn on the Today Show with your TV’s remote control. You listen with half an ear as Katie Couric interviews Madonna. Outside a few birds chirp in the cloudy morning air.
There’s just one problem. A big problem. You have actually died in your sleep and, unfortunately, have gone to hell.
You look around. Your bedroom is a cheap facade. The bird outside is a mechanical contrivance that flies away screeching. The TV set disappears to be replaced with a devil. He approaches.
The devil comes so close you can smell his hot, sulfurous breath. “I have a game of chance for you to play. If you win the game, you can go to heaven, but if you lose you must stay forever in hell. You can only play the game once.”
“This sounds ominous.” You try to appear calm.
“Ha! You’ve got no choice. If you play on the first day you have a one-half chance of winning. If you play on the second day you have a two-thirds chance of winning. If you play on the third day, you have a three-quarters chance of winning, and so on.” He hands you a card that reads: 1/2, 2/3, 3/4, 4/5,…
The devil stamps his clawed foot on the warm ground. “My question to you is this. When is the most rational day for you to play?”
Pondering this question, you follow the devil as he leads you across a strange land of varicolored weeds and a few stunted trees. Occasionally you see gases oozing from mist-covered swamps and reeds and cattails moving in some of the smaller marshes. In these pools stand gibbons of various sizes and colors. Everywhere is the smell of decay—the putrefaction of nearly liquid masses resembling the rarefying remains of long-dead gibbons. By comparison, this stench makes the stink of a cesspool seem like a new perfume by Chanel.
You step back in terror and begin to ponder the Devil’s Offer. “If I wait a whole year before playing, my chances of winning are a very good 0.997268. This number comes from 365/366.”
The devil nods. “Yes, but if you wait a year and a day, your chances are increased by 0.000007.”
“It seems hardly worth delaying for that tiny increased chance of winning.”
“Don’t be a fool. It’s true that 0.000007 seems tiny, but the reward of winning is infinite. Eternal bliss in heaven with attractive angels catering to your every whim. Don’t you think a finitely large extra chance of winning something infinite is worth more than your finite suffering spending one more day in hell?”
The devil may have a point, but you are distracted. How did you get here in hell? Is it real? What do you do when something so absurd, so out of place in the scheme of everyday living, takes place? Oh, one can speculate about what one should do if this or that happens, but no one can say what action one would take when the fabric of reality begins to tear. And when it happens to you on that hot summer morning, you do not stand there long trying to figure out a rational, scientific explanation for it all. It would almost be funny, if you were not living through the experience.
You think about what the devil said about your chances of winning freedom. The devil seems right when he says that waiting a year and a day is better than waiting a year. In terms of game theory, the utility of waiting a mere 24 hours (the extra chance of winning multiplied by the infinite payoff) will always be infinite. Perhaps you should wait in his scenario. But given this logic, it always seems worth it for you to wait an additional day. And that means there will be no limit to how long you should wait in hell. You will end up remaining in hell forever in order to increase your chances of entering heaven. What do you do?
“I’ll return when you make your choice.” The devil bows and fades away into fetid chasms of empty air. He leaves you there, alone. Very alone.
Every night you go to sleep to the eternal rhythms of the gibbon howling. Sometimes your hands itch, and after a few weeks, strange fungoid growths begin to appear on the palms of your hands. Your nails turn black—the same color as the gibbons surrounding you. You begin to speculate that you are part of some combined genetic and electronic experiment, that your body is regressing toward a more simian shape. If this were true, perhaps the gibbons around you at one time had a human form. But then you discard this idea. This must be hell. You saw the devil. It is time to make a decision about when to play the game.
Dear God. What do you do? Can you hope to escape from this fantastic nightmare?
MUSINGS AND SPECULATIONS
Down, down to hell; and say I sent thee thither.
—William Shakespeare, Henry VI
This scenario and paradox was proposed in 1988 by Edward J. Gracely in his paper “Playing Games with Eternity: The Devil’s Offer,” published in the journal Analysis.1 Although seemingly simple, this existential dilemma touches both on the concept of infinity and on certain theological assumptions.
Let’s assume you are in hell and talking to the devil again. Do you think the hope of entering heaven someday in the future lessens your suffering in hell? If so, then perhaps it is unsatisfying to play the game and risk losing that hope and risk losing heaven. Authors Glenn Erikson and John Fossa say, “Compared to waiting in hell forever without hope of escape, deferring the playing of the game forever might be the wisest course. Heaven itself may have no pleasure comparable to that of anticipating leaving hell for heaven.”2 On the other hand, the longer you delay, your chance of winning becomes so great that you would be foolish to delay a day more.
This scenario reminds me of the stereotypical miser who hoards millions of dollars, never wanting to spend them. Wouldn’t you be torturing yourself to keep pushing the day of playing back further? The crux of the problem is that we humans are not able to differentiate among the chances of winning because the infinite payoff makes each increase in our chances “infinitely desirable.”3 What would you do?
* * *
I recently had a chat with Ed Gracely, author of the original “Devil’s Offer” article. Gracely is a quantitative psychologist at MCP Hahnemann University in Philadelphia, and his interests include philosophical ethics and ethical decision making. He also has been long fascinated by the ethical implications of infinite sequences. Gracely writes to me,
Suppose, for example, that a good deed of any sort begins an infinitely expanding series of similar events, growing exponentially in importance, perhaps even through alternate universes. Let’s assume the good deed’s value doubles every ten minutes. A deed done now has a current value of 1, which will increase to 2 in 10 minutes. A deed done then will also have a value of 1 at the time it is performed. After about 100 doublings, the absolute difference in value between the deed done now and one done 10 minutes after it is on the order of 1030. Clearly, this absolute difference heads toward infinity unless the sequences stop. Because “infinity” trumps probability, it doesn’t matter how unlikely you regard these scenarios to be. The mere conceivability of them creates questions of infinite magnitude! Should we really rush to perform good deeds now, rather than waiting a day? Are we losing infinitely by not doing so? Clearly, rationality does not permit us to act upon these possibilities, but it is frustrating that infinity leads to yet another set of fundamentally unsolvable problems. Depending on the precise formulation, this may be a large number problem or one based on infinity. I think that philosophical ethics needs a good approach to both large number problems (like heaven and hell lasting 10100 years) and to true paradoxes introduced by infinity per se.
Gracely had been thinking of these examples of infinite sequence problems when the idea of the “Devil’s Paradox” came to him. He found the problem particularly fascinating because it involved a situation in which there was a true paradox, not merely a difficulty or conundrum. Gracely has no solution, nor has anyone submitted one to Analysis, as far as he knows. Gracely writes,
If we made hell last 10100 years, there would be a calculable solution, but there is no solution if hell is of infinite duration. The protagonist is faced with an impossible-to-solve dilemma unless he or she makes an existential leap at some point and says, “Now!” That may well be what the scenario calls for, but my utilitarian soul rebels!
* * *
This Devil’s Offer is reminiscent of a game I published a few years ago called “Slides in Hell.”4 On a hot summer day, I was visiting a local playground where I came across the most startling piece of recreational equipment. It was a metallic slide with a large hole punched in the chute. To this day, I can’t think of any reason it was there, because it seemed rather dangerous. Children usually slid from the top of the slide to the bottom, but it seemed as if a small child could get stuck or even fall through the hole in the chute.
The image of this strange slide stayed in my mind for several months and stimulated the following mental exercise: You are in hell. Tongues of lava and fire seem to defy gravity as they lick the cavern walls, undulating obscenely to a music you cannot hear. The ceiling of the cavern is like a flock of bats on fire.
Satan asks you to consider a metallic slide punched with ten large holes that are equally spaced from top to bottom. The porous slide is such that you’d certainly fall through at least one of the holes during your descent.
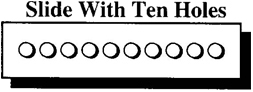
For this uncomfortable problem, let’s assume that each time you encounter a hole you have a 50 percent chance of sliding through it and into a vile oleaginous substance beneath the slide. For example, when your body passes over the first hole, one out of every two times you’d expect to fall through the hole into the loathsome liquid below.
Satan asks you a question. He offers you $1 million and your freedom if you can correctly guess which hole a person would fall through as he or she descended the slide. Which hole would you choose?
Soon the number of questions starts escalating. Here’s a summary of the most interesting ones Satan asks:
• If you were a gambling person, which hole would you bet a person would fall through?
• How many attempts do you think it would require for a person to slide from the top of the slide to the bottom without falling through a single hole?
• Go back up to Earth. All the people on Earth have lined up to slide down a longer, more horrifying slide containing 100 holes. If people go down the slide at a rate of one person per second, when would you expect the first person to arrive at the bottom of the slide without falling through any hole? After an hour? A day? A decade?
It turns out that an analysis of this problem is not too difficult. The chance of falling through the first hole is 50 percent. The probability of reaching and falling through the second hole is less. Specifically, it is the probability that a person didn’t fall through the first hole times the probability of falling through the second hole: 0.5 × 0.5 = 25 percent. For the third hole, we have 0.53 = 0.125. This also means that, in a large enough sample, 1/2 of the people will fall through the first hole, 1/4 through the second, 1/8 through the third, etcetera. We can create a table showing the percent chance of reaching and falling into each hole as a person descends the slide:
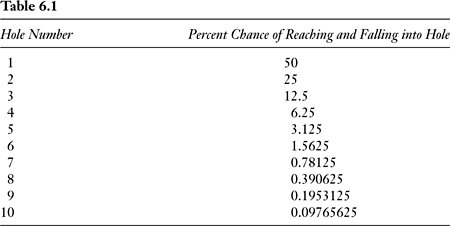
Your chances of reaching and falling into the final hole are slim indeed—only about nine hundredths of a percent. Most mathematicians I asked said that because they were limited to selecting one hole, they would place their money on hole number 1. In other words, individuals would be most likely to fall through this hole. However, one respondent said he would not bet at all because the best chance is only a 50/50 chance.
As for the second question about how many attempts it would take to reach the bottom without falling through any hole, note that the chances of reaching each succeeding hole are the same as for reaching and falling into the previous one. Therefore, the chances of passing over all the holes are the same as of reaching and falling into the last hole. Therefore, the probability is 1/1,024 = 0.0009765625; that is, 1,024 attempts would be required by a person, on average, to reach the bottom. Some people I queried suggested that they would bet on a number less than this because the actual events can happen in any order. For example, J. Theodore Schuerzinger from Dartmouth University notes that because 1/210 (or 1/1,024) people would make it all the way down the slide without falling through any of the holes, this means that 1,023 out of 1,024 people would fall through one of the holes. He notes:
Using the formula (1023/1024)x = ½, we can determine that out of the first x people to go down the slide, there is a 50% chance that one person will make it down without falling through a hole. The solution × = 709.4 satisfies the equation. Thus I would bet that a person would make it all the way down on one of the first 710 attempts. In other words, after 710 attempts, the chance of someone succeeding exceeds 1/2.5
What happens if all the people on earth lined up to go down the 100-hole slide at a rate of 1 person per second? The probability of falling through the last hole is a minuscule 0.5100 = 7.88 × 10–31. The average number of tries that a single person must make to finally arrive at the bottom is 1/0.5100= 1.26 × 1030 or, to be more precise, it would require
1,267,650,600,228,229,401,496,703,205,376
attempts, on average, to reach bottom. (Your gluteus maximus muscles had better be in good shape before you attempt such an experiment.) In other words, we may see one person slide down over all the holes every 1.26 × 1030 attempts. At 1 person/second, we can compute that it would require, on average, about 4 × 1022 years, much older than the age of the universe. Note also that this would require many more people than the world population can offer. Therefore, no one will reach the bottom of the slide, or, as one respondent said, “they will all try and fail (assuming everyone only gets to try once), or die waiting in line.” Using a logic similar to that for the 10-hole problem, after (2100–1)/(2100) attempts, the chance of someone succeeding exceeds ½.
* * *
Many of you may picture the devil as ruler of hell, inflicting physical and mental pain on others. But this portrayal of the devil is nowhere in the Bible. In the Bible, the devil is just another captive.
The Old Testament mentions Sheol, an unpleasant place in the afterlife from which the godly would be delivered. The New Testament mentions Hades and Gehennah. Hades, a word borrowed from Greek mythology, is a general term for the afterlife. Gehennah, on the other hand, was a place of everlasting torment. Back in the time of King Solomon, there was a temple in Jerusalem called Tophet where infants were burned. Tophet was in the Valley of Ben Hinnon, later called Gehennah in the New Testament. In this valley, children were sacrificed to the Canaanite god Molech. The area was later used as a garbage pit, where fire burned almost continuously. Thus, Gehennah came to be a metaphor for Hell.
The ancient Jews believed that Sheol or Tophet was a gloomy place of departed souls that were not tormented but wandered about unhappily. Gehennah, in the New Testament, became a place of punishment.
Jews and Christians refer to the Devil as Satan, a fallen and arrogant angel. In parts of the Old Testament, Satan is not God’s enemy but rather a challenger or accuser. The word devil comes from the Greek diabolos, meaning “slanderer” or “accuser.” The word Satan is the English transliteration of a Hebrew word for “adversary” in the Old Testament.
In the Old Testament, Satan gambles with God about the faith of Job. Later, in the New Testament, Satan becomes the “prince of devils” and has names such as Lucifer (the fallen angel of Light), Belial (lawless), and Beelzebub (Lord of Flies):6
All the people were astonished and said, “Could this be the Son of David?” But when the Pharisees heard this, they said, “It is only by Beelzebub, the prince of demons, that this fellow drives out demons.” (Matthew 12:24–27)
What harmony is there between Christ and Belial? What does a believer have in common with an unbeliever? (2 Corinthians 6:15–16)
For Christians, Satan’s job is to tempt man to commit immoral acts. Muslims believe in Iblis, the personal name for the Devil. They also call him ash-Shaytan, which means “the demon.” In the Koran, God tells Iblis to bow in front of Adam, the first human. Iblis refuses.
Seven Old Testament books and all New Testament writers refer to Satan. In the Middle Ages, theologians debated about how a supernatural being like Satan could exist in a universe governed by an omniscient, omnibenevolent, omnipotent God. Many came to believe that Satan was not an actual being but a symbol of evil.
An important part of the wonder of the Jewish Bible, and especially of Genesis, is the imperfection of every character in the drama, including the One who plays the leading role. The Jewish God is great and powerful, but even He is not perfect—at least not in the beginning.
—Alan Dershowitz, The Genesis of Justice
Heaven, n.: A place where the wicked cease from troubling you with talk of their personal affairs, and the good listen with attention while you expound your own.
—Ambrose Bierce, “The Devil’s Dictionary”
I am seventy and in mediocre health. It is not beyond the realm of possibility that I might be meeting God in the not-too-distant future. If I do, it will come as a surprise, but I’ve been surprised before. No doubt He would have a number of questions to put to me. I know that I would have a number of questions to put to him. But one question I am sure He will not put is: Why didn’t you believe in Me? For one thing, He will know. For another, He will regard it as irrelevant to the matter at hand.
—Ralph Estling, Skeptical Inquirer