MEASURING THE COSMOS IN TAURUS
THE EFFECT OF THE seasons, sun, moon, and the periodicities of the planets as experienced on Earth give celestial time a definite pattern. Stone Age stories about the sky could be extended only by moving on, by gleaning a better understanding of the exact order of celestial events from the stable base of Neolithic agriculture. Such a realization led to the cultural advance that we now call the Megalithic period, during the Age of Taurus. The Megalithic period evolved a unique approach to measuring and calculating, a method that was quite distinct from that of our present science and mathematics, and these unfamiliar methods were recorded in stone. Their monumental architecture, required to measure the numerical properties of celestial time periods, developed from some very simple ideas about counting and geometry.
THE DEVELOPMENT OF THE DAY-INCH
The primary unit of measure used in the Megalithic period was the day itself. Counting days allowed significant achievements: for example, the lunar month can be counted over two entire periods (59 days). At 29.53 days, the lunar month is nearly 29.5 days, which means that two months equal 59 days, to nearly 1 part in 1,000. This provides therefore a very accurate approximation without much sophistication in measurement, a recurring theme in megalithic astronomy, where achievements were made possible through fortunate astronomical circumstances.

Figure 2.1. One of many alignments at Carnac, Brittany, where, for unknown reasons, many rows of stones exist at about 23 degrees east-northeast through the landscape
Such counts are found in the Stone Age as sets of notches or other marks scored on bone. These marks later came, by the megalithic, to be made with equal spacing using a size similar to our present inch—a digit related to the width of a thumb. An inch measure has many uses; it is conveniently small, and a great number of them, used in a longer count, generate lengths that can be used to construct geometrical structures through which time periods can be compared as objective ratios. The adoption of a uniform length for each day also allowed the detection of fractions of a day when these counts were employed geometrically: 1/8 inch could be visible as 1/8 day (three hours). The resulting system of metrology allowed the study of the cosmic time ratios, such as those between the solar year and lunar year (of twelve lunar months). This activity appears to have been the precursor for our system of metrology—a system based on ratio—inherited as the historical measuring systems used throughout the world.
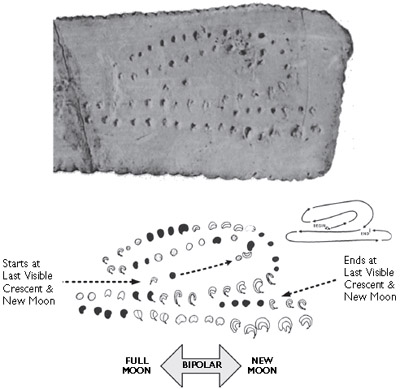
Figure 2.2. Engraved and shaped bone plaque from the rock shelter site of Blanchard (Dordogne) from the Aurignacian period, about thirty-five thousand years ago. This was one of many bones that Alexander Marshack, in his book The Roots of Civilization, interpreted as being based upon the phases of lunar months.
The four years between identical sunrises on a horizon mark could be counted as 1,461 day-inches, and the division of this by 4 (by folding a marked rope twice) results in a 365.25 day-inch year. Such direct measurements contrast with our present methods, in which measurements are abstracted from a measuring apparatus using numbers—that is, through the use of numerical notation. Instead, Megalithic astronomers maintained a direct connection between the apparatus and the measurement by using geometrical techniques based upon inch counts.
This approach enabled powerful calculations using exactly the type of geometries we find at Megalithic sites. These frequently employ right-angled triangles, which allow the comparison of day counts without using our trigonometric methods: the difference between the two longer sides of a right-angled triangle presents the cosine function of our trigonometry. Metrology, a technology involving measured lengths, could incorporate time measurement into such triangles once a constant day-inch is used when counting.
STUDYING THE LUNAR AND SOLAR YEARS
The most obvious time proportion to study is the difference between the 12 lunar months of a lunar year (354.367 days) and the days in a solar year (365.2422 days), which is slightly longer. As already stated, day-inch counts can give reasonable results for the length of the solar year and lunar month, at least as good as 365.25 day-inches and 29.5 day-inches, respectively. The lunar year is then 12 × 29.5 days, or 354 day-inches long. However, a longer count of 3 lunar years (36 lunar months) yields an extra day to the count—1,063 days—and this is then ten times more accurate than a 29.5-day lunar month, being accurate to almost 1 part in 10,000. It is only 2.5 hours short of the correct time for 36 lunar months (1,063.1 days).
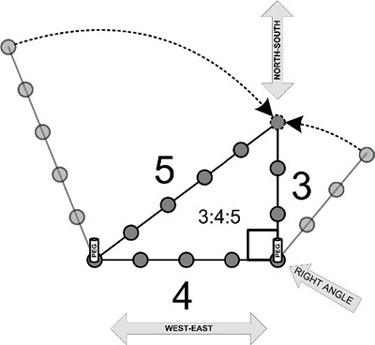
Brittany is one of the oldest Megalithic regions, and the region around Carnac (dated around 5500 to 5000 BCE) has many complex monuments that relate to the sun and moon. At the latitude of Carnac, the sun’s rising and setting points at winter and summer solstices has the strange geometric property of forming the first Pythagorean triangle relative to the east-west axis. Many such triangles, with side lengths of 3, 4, and 5 units long, were constructed at Carnac, and within them, two sides define a right angle aligned to the cardinal points. The longest side (5 units long) was then aligned to the direction of the sun at sunrise or sunset during both solstices.
The presence of megalith builders at this latitude demonstrates that the simplest of all the whole number triangles was understood at that time and that it lay at the root of these builders’ geometrical thinking. This triangle affirms their choice of this latitude based on this simple triangle, as it has the practical application of easily establishing sight-lines to the solstice sunrise and sunset.
Such a triangle can be constructed using a rod of any length to mark three sides of a triangle (3, 4, and 5 units in length). In fact, such whole-number triangles are best constructed on the ground using ropes, a method in which the right angle makes itself during the process of manipulating a regularly knotted loop of rope. Since day-inch counting lengths can be compared using a right-angled triangle, a pegged rope ensures that an accurate right angle can be formed in triangles whose sides were not 3-4-5, as shown in figure 2.4. This technique could then be used to provide the right angle for triangles with longer sides based on day-inch counts.
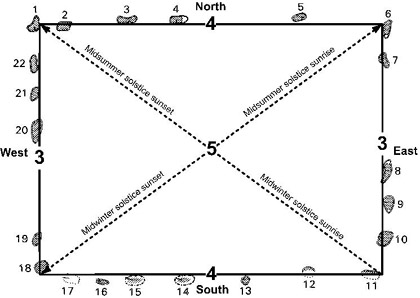
Figure 2.3. The usefulness of 3-4-5 triangles at Carnac in aligning to solstice sunrises and sunsets. One of the clearest examples of this geometry can be found within the Crucuno rectangle. Alexander Thom’s 1973 survey of this rectangle, despite having many of its stones disturbed, fallen, or ambiguously re-erected, demonstrated that 3-4-5 triangles were regularly incorporated in the Megalithic structures at Carnac.
Figure 2.4. A rope with twelve equal divisions comes together to form a 3-4-5 triangle and an accurate right angle. Any Pythagorean triangle made of whole numbers on each of its sides was used to build right-angled triangles with day-inch counts on their two longer sides, allowing Megalithic astronomers to geometrically study celestial time ratios.
Having established that the solstice sun always shone on the longest side of a 3-4-5 triangle at the latitude of Carnac, the Megalithic astronomers chose the solstice sun alignment to begin a count in day-inches. In 2009, Robin Heath discovered an inch-encoded sightline at the site known as Le Manio, within a construction called the Quadrilateral (see figure 2.5). This discovery supported my theory that day-inch counting lay at the heart of early Megalithic astronomy.1 The length of the line in day-inches is found to equal 3 solar years (1,095.75 day-inches), or as we would say today, this line is three years long (we still refer to time as having a length).

Figure 2.5. The day-inch counting line defined by the midsummer solstice at Le Manio Quadrilateral. Photo of the site from the northeast. Photo by Robin and Richard Heath.
In a 3-year count, it is natural to mark each day-inch within which a full moon occurs. Thirty-six such full moons result over 3 lunar years, if the count begins on a full-moon day, and the extra length required to reach the end of 3 solar years reveals the difference between 3 lunar and 3 solar years: just over one further lunar month.
Forming a Soli-lunar Triangle
The Quadrilateral at Le Manio was built using small megaliths that touch, so as to form low walls called kerbs punctuated in places by gaps, and some gaps were evidently symbolic as with the (solsticial) “sun gate” from which the three-solar-year, day-inch count began. A triangle was formed from the counts by dropping one end of the 3-lunar-year count until it formed a right-angled triangle that traveled along the southernmost kerb of stones that now make up the Quadrilateral (see figure 2.6 and the box How the Megalithic Yard Was Defined at Carnac’s Le Manio—below—for a more detailed description). This enabled the relative proportion of the two types of years—solar and lunar over three years—to be viewed as a geometric ratio (which is what the slope angle of any right-angled triangle represents). In math-speak, a solar hypotenuse above a lunar base results in the ratio between the two lengths, which today we call the cosine of the angle between the two sides, and the base ÷ hypotenuse = cosine. This angle is an invariant property of the sun and moon, and so, wherever this angle or triangle arises, this astronomical reality is presented.
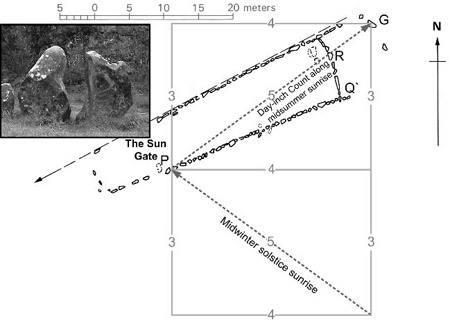
Figure 2.6. Photo of the distinctive sun gate at Le Manio, including stone P, where the counting began
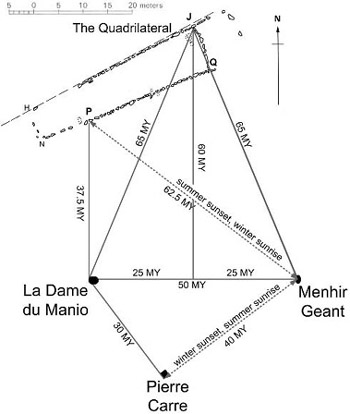
Figure 2.7. The local geometrical interpretation of Le Manio using 3-4-5 and 12-13-5 triangles within an integrated scheme. The Association pour le Connaissance et l’Etude des Megalithes, or ACEM, is continuing the work that was done over the last 20 years at Carnac.
How the Megalithic Yard was Defined at Carnac’s Le Manio
The Le Manio site probably represents early and later developments, and we can now propose a timeline for the earliest part of this development.
1. A suitable line was established that ran along a sightline aligned to the midsummer solstice. Stone P was erected to indicate the starting point for a day-inch count, and the groove in stone G is aligned to midsummer sunrise seen from sun gate P.
2. A 3-solar-year day-inch count was started that progressed from sun gate P toward stone G. This could have used a measuring rod (ruler) designed to accommodate a counting marker.
3. Full moons could have been shown in the count (as with an inch marker made of quartz) as the count progressed to its 3-year end. Stone R was eventually installed after three years and dressed to provide an accurate reference to the end of the count.
4. The distance between the 36th full moon (lunar month) and the end of the 3-year count equals 32 5/8 inches. This length be came the standard megalithic yard of 2.718 feet used later within the Le Manio site and beyond. A standard rule of this length could then be constructed, possibly calibrated as a ruler using a set of inch markers, grooves, or notches.
5. A triangle was formed to present the differential length between the solar and lunar counts. A second rope, whose length corresponds to 36 full moons (lunar months), was attached to the left end of the original rope (at sun gate’s point P; see figure 2.7). The new rope (36–full moons long) is then pivoted downward from the joining point at P until its end stands below the end of the longer (the 3-lunar-year-count) rope. The two rope ends define a third side that forms a right angle between itself and the count for 36 months. A 12-section rope would have helped achieve such a right angle using a 3-4-5 triangle, as discussed above.
6. Stones R and Q (see figure 2.8) were only later prepared and installed to mark the end of the 3-solar-year count and the end of 3 lunar years, respectively, and to set the triangle in stone down two of its sides as part of the Quadrilateral. The original count forms the hypotenuse between the sun gate’s point P and stone R, between which the count (the hypotenuse) can still be measured.
Whenever a megalithic yard was not available, a 3-year day-inch count could provide it from a standardized inch using the above geometrical procedure.
The slope angle of a triangle’s longer side relative to its base causes any sub length of the base to correspond to a longer sub length above it on the longer side (the hypotenuse) according to a fixed proportion. A lunar-month count on the base therefore points to the longer mean solar month (1/12 of a solar year) on the longer side. This difference in the growth of a hypotenuse relative to its base results from the proportional growth in length between the two sides. This geometric structure enabled a Stone Age culture to make scientific discoveries through constructing metrological and geometrical tools on the ground.
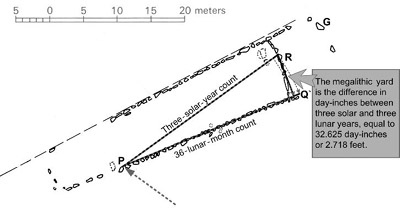
Figure 2.8. The triangle constructed at Le Manio from counting 3 solar years and dropping the (initially) parallel count of 3 lunar years in order to create a right-angled triangle.
Once they generated such a triangle, the builders could see the proportionality between lunar years and solar years: lunar months on the base translate to solar months on the solar count hypotenuse. This naturally projects the division by 12 of the lunar year (by lunar months) into an equivalent division of the solar year (by 12 solar months). These mean solar months are not marked by any directly visible phenomenon, as they are with the moon (where a full moon divides the lunar year into 12), but this triangle naturally presents the division of the ecliptic into a zodiac of twelve equally spaced regions through which the sun travels through the year. It is likely that the twelvefold division of the sun’s yearly journey through the stars was triggered by this clear projection of the lunar year onto the solar year and that this was discovered when the two time periods were compared using a triangle in the Megalithic.
This expansion of the lunar month into a solar month generates the difference between the shorter, lunar base and the longer, solar hypotenuse after 36 (3 × 12) expansions. At Le Manio, the count appears to have generated a difference between 3 solar years and 3 lunar years of 32 and 5/8 inches, or 2.72 feet, which was the length discovered independently at Carnac by Alexander Thom, and was the length he named the megalithic yard.2 It is important to note that this yard is shorter than an English foot yard, which is 36 of the same inches.
The builders therefore appear to have used a day count to establish their megalithic yard, defined as the excess of 3 solar years over 3 lunar years in day-inches. This unit of length was then employed for subsequent constructions, such as the 3-4-5 triangles, using measuring rods or ropes based upon such day-inch counting.
THE METER AND THE MOON
My brother and I returned to Le Manio at the March 2010 equinox in order to see how my theory of day-inch counting would correspond to an accurate survey of the Quadrilateral.*4 We had realized that the solar-lunar triangles (there is also one for 4 solar years) were calibrated in day-inches rather than the expected megalithic yards because they were real day counts. A number of additional facts emerged that further explained the unusual design of this megalithic monument.
The third side of a soli-lunar triangle for 3 years has a length exactly equivalent to 9 lunar months of day counting. The 36 months of the base can therefore be divided by this length exactly 4 times, because 36 ÷ 4 = 9. This provides a geometric method to reconstruct this triangle over any period, not just 3 years, to generate day-inch counts without actually counting the days.
By generating 4 squares of equal side length equal to 1/4 the base, the size of the diagonal (the triangle’s third side or hypotenuse) is then the solar-year count, which is 12.369 lunar months long (as a day count)—the square root of (a) the square of the base of 12 months plus (b) the square of the third side of 3 months. (Today, we use the Pythagorean theorem, adding the squares of 12 and 3, 144 + 9 = 153, which has a square root of 12.369 months.) The achieved accuracy of this geometrical diagonal relative to a day count for the given number of solar years is 1 part in 20,000, which is very accurate. The geometry of four squares therefore exceeds the practical accuracy of any actual day count; it is within 45 minutes per solar year, and can thereafter replace day counting as a method for reproducing this triangle.
The four squares geometry must have become a portable procedure for the reproduction of the soli-lunar triangle (both its slope angle and actual day-inch count) for any chosen number of solar years. Its reproduction probably required the evolution of a standard measuring unit with which to build this geometry—a unit more convenient than 29.53 inches. Such a natural unit emerged during our survey when we noticed that 36 months measured exactly 27 meters on the base for 3 lunar years. The modern meter is 36/27 (4/3) of the day-inch count for a month, because 3/4 meter equals 29.528 day-inches. Three meters—118.11 inches—then becomes a useful measure equivalent to a 4-lunar-month day count. This 3-4 relationship between the month and the meter plays out between the 3-year and 4-year triangles at Le Manio, because the 4-lunar-year base is then 36 meters, the number of months in 3 lunar years.
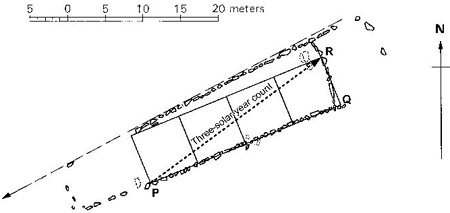
Figure 2.9. Four-squares geometry, with a diagonal that represents the solar year. Once discovered, this geometry leads to greater accuracy than day counting and provides a portable geometric device for reconstituting the soli-lunar triangle’s day-inch count.
The 4-year triangle at Le Manio shows the meter’s utility very clearly, because it is made up of 4 12-month squares, each of which is 3 meters × 3 meters in size. Whereas the eastern corners and southern kerb, defined by the 3- and 4-year triangles, can be read in meters as well as inches, lunar years are more easily counted as meters that equal 4/3 months, because a lunar year is 12 months long and 9 metres long in day-inch counting.
Thus the Quadrilateral is a perfect symbol of the essential sun and moon ratios, built using the number symbolism of metrological lengths. The Quadrilateral appears to have been built exactly at the latitude at which it was possible to fit these cosmic ratios, as triangles, between the midsummer sunrise and the east. This use of latitude implies that the builders had already mastered the additional skills of determining latitude and surveying. It also implies that these day counts were not originally conducted at Le Manio, but had led to a search for the latitude at which these two triangles would fit in this way. The monument at Le Manio was probably built as a recapitulation of early Megalithic knowledge, written in stone as a perfect statement of what the builders knew and how they had come to know it at some time prior to 4000 BCE.
The use of counting lengths and geometry was the ideal mechanism for the people of the Late Stone Age to have developed numerical thinking, prior to, and in preparation for, the development of number notation and its associated mathematics. Such use enabled a Megalithic science that could tell the story of cosmic time—prior to the known history of mathematics.
THE EFFECT OF AN INTELLIGIBLE COSMOS
It is clear that the Megalithic astronomers pursued very simple strategies that successfully unlocked some remarkable characteristics in the relative time periods of the sun and moon as seen from Earth. Their methods required the use of geometry and the metrological skills that are found at megalithic sites as part of an ancient wisdom thought to have existed in prehistory and probably mythologized as the story of a lost high civilization called Atlantis.
Ancient scientists had probably not detached themselves from the religious concept that the universe was a creation. They could explore phenomena as meaningful expressions of order, and in their view, this would bring them into contact with an intelligence that had created this order. This belief, within precessional time, proved to be a developmental process for their consciousness and its evolution. It left behind our historical metrology still based upon the inch and foot, though ancient scientists’ astronomical discoveries soon became garbled or lost altogether to our histories.
The universe, it seems, has something to say, and this can make us more intelligent, as in the principle of intelligibility within the sun-moon system of time. Consciousness is only truly available in the confluence of the intelligible and the intelligent. This requires that a world should be intelligible and life arise within it that can be intelligent, as in the form of the story in which the blending of these two create a narrative structure for consciousness.
If a stick is 19 units long, and we point it at the North Pole from the ground near Stonehenge, in England, the base of the triangle created is 12 units, and the excess of the hypotenuse over the base is 7 units. This means that the megalithic yard, royal cubit, and English foot relationships of 19/7, 12/7, and 7/7 feet, respectively, were all implicit at the latitude where these units are found within monuments in southern Britain.
Such synchronicity between culture and cosmos suggests a helping hand from Nature in that day counting can achieve metrological ratios and simple geometries that can effectively describe the sun and moon. This was also a work that only became possible within a Neolithic revolution. If the cosmic ratios are intelligible as geometrical ratios and interrelated periodicities, then an early human culture will always be able to achieve an exceptional degree of knowledge by using the direct methods of the Megalithic.
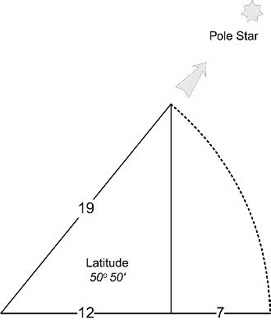
Figure 2.10. The strange coincidence that the key ratios of the megalithic yard (19/7 feet), English foot (7/7 feet), and royal cubit (12/7 feet) are implicit in the polar sightline at 50 degrees, 50 minutes of latitude, just south of Stonehenge. The perfect megalithic yard would correspond exactly to the ratio between three lunar and three solar years. We call this the Astronomical Megalithic Yard, or AMY, and its value is almost exactly 19/7 feet long.
Two theories could account for how such triangles work so closely with the structure of astronomical time, both suggesting that the cosmos has a designed nature. The first theory proposes that these geometries were the nominal targets for a design process natural to the creation of planetary systems in which life like ours can arise. The second theory proposes that the organization of time then became intelligible, through its simplicity, thus ensuring that early astronomers could develop geometries and ratios, allowing a glimpse of the type of intelligence responsible for the creation.
The convention is that angels or a demiurge are beings rather like us and that they design as we do. It is more likely, however, that there is a form of intelligence within the cosmic structures that arrives at certain types of solutions within the number field. As Johannes Kepler suggested, God geometricizes. Such an intelligence would be expressed within cosmic phenomena. Though the present paradigm is of intelligence coming as a result of biological evolution alone, our level of development is probably only a prerequisite for receiving and acting out a common cosmic intelligence.
Though the theory of intelligent design is disapproved of in modern science—because material causes come about through blind forces and natural laws—this does not mean that a theory involving intelligent design is inherently disreputable or that no new structural laws remain to be discovered. Consciousness and higher intelligence are not purely objective; there is always a subjective component that relates to moments of intelligence in our lives that we cannot repeat, yet a scientific experiment must be repeated in order to prove a result. In considering whether precession affects human history, the Megalithic peoples apparently discovered and were affected by the near-perfect geometrical coincidences they found, ready made, between key time periods. They demonstrated intelligence in comprehending the order of time and being able to realize these relationships in monuments that measured and made them manifest.
Limiting our science to repeatable causation only limits any theory of how time’s coincidences play a role in structuring actual situations, and such a science has made the Megalithic achievements unintelligible. The intelligibility of the natural world requires that higher intelligences act through special opportunities that, though seeming impossible or unlikely beforehand, are routinely accepted once they have happened.
THE LONGER CYCLES OF THE MOON
Sometime after the work at Le Manio, Megalithic astronomers discovered that after 19 years, the sun, moon, and stars return to almost an identical position relative to each other. This fact, which we call the Metonic period (after a Greek named Meton) was less easy to observe than it is to predict based upon the soli-lunar triangles these astronomers had discovered. It is possible, for example, to build a triangle that shows exactly 7 months separating the 228 months of 19 lunar years, and the 235 months equaling 19 solar years.*5
On the other hand, similar eclipses recur every 223 months, a cycle called the Saros, which lasts 18 years plus 10.875 days (the excess in day-inches for one year). There are exactly 12 lunations in difference between the Saros and the Metonic cycles, which means it is true that the eclipse cycle is quite synchronous with the sun and moon cycle of 19 years. Some basic facts about why eclipses occur reveal another type of year that punctuates lunar and solar years: an eclipse year.
The moon in its orbit (angled to that of Earth) must cross, in two places, the sun’s path. When the sun is at one of these nodes, a crossing by the moon causes a solar eclipse at the sun’s position or a lunar eclipse at a position opposite the sun. The sun can visit these eclipse nodes only twice in its yearly round; therefore there are two eclipse seasons in a year, but because the moon’s nodes move retrograde along the sun’s path, the sun meets a given node once every eclipse year of 346.62 days (18.618 days short of the solar year).
This third, eclipse, year occurs 19 times within the Saros cycle, which is itself 12 months short of the Metonic cycle of 19 years, which is 5 months more than 19 lunar years. The cycles are therefore interrelated and have in common the number 19. The regular punctuation of suitable conditions for lunar eclipses in particular means that it is very easy to deduce that the number of eclipse years in the Saros cycle must exactly equal 19 eclipse years.
An eclipse year is therefore 223/19 (or 11 14/19) months in length, which equals 346.6 days, an accurate figure that can be refined through long counts between many eclipses. Based on this estimate, eclipses can be predicted by actively tracking the location of the nodes on the zodiac. This allows the prediction of eclipse conditions without knowing that an eclipse occurred one Saros period ago. A suitable device for this prediction has been found in the form of the Aubrey Circle of holes around Stonehenge, through which, using markers for the sun, moon, and lunar nodes, a sidereal simulator of the sky can be constructed.3
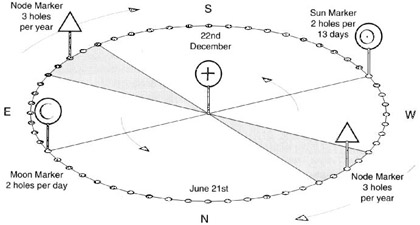
Figure 2.11. The application of Stonehenge’s Aubrey Circle of 56 postholes as a circular simulator that uses simple rules to track the sun, moon, and lunar nodes as these progress through the ecliptic zodiac. The slight cumulative errors this simulator generated could be corrected when an actual eclipse is slightly late or early. The sun’s path during the year and the stars behind the moon also make this “clock” a sidereal map of the zodiac “in the round.”
The triangle for the lunar nodal period, viewed as a 346.6-day to 365.25-day triangle, displays the interesting feature of an intermediate hypotenuse (at the point that divides the third side according to the golden mean; see figure 2.12) close to the lunar year’s length.
This 18.618:19.618 triangle, found in the Megalithic structures in Brittany and Britain, is the Type B–flattened circles identified by Alexander Thom. See figures 2.13 and 2.14.4
THE MOON’S RELATIONSHIP TO PRECESSION
The precessional cycle of equinoxes does not appear to be related to the moon’s nodal period of 18.618 years. Yet the nodal period would divide into the length of a precessional age if it were 1/15 longer, corresponding to a pure half tone increase of 16/15. In order for this to be true, the length of an age would be 2,145 years long and precession 25,740 years long. Because the modern scientific estimate for precession is 25,750–25,770 years, 1/12 of this is within a few years of the modern estimate; thus the moon’s nodes appear numerically related to the precessional cycle, in addition to the moon stabilizing Earth’s tilt and hence precession itself.
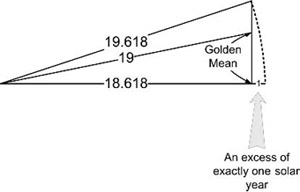
Figure 2.12. The triangle for the lunar nodal period where N = 18.618: as with other N : N + 1 triangles, the difference between the base of N units and the hypotenuse of N + 1 units is very significant—as with the megalithic yard being the difference within the three-year triangle. In this case, the difference emerged from the fact that there are 19.618 eclipse years in 18.618 years, the nodal orbital period. But it is also true that these two types of year, the eclipse and solar years, differ by 18.618 days, because the nodes move one day of solar motion in the time that the sun moves 18.618 days. The 19-year Metonic cycle then sits at the golden mean point on the third side (a property of this type of triangle with non-integer, fractional parts equal to 0.618).
The figure of 2,160 years for an age, adopted since Plato’s time, is based upon an ideal harmonic form (see chapter 3) in which the resulting precessional cycle of 25,920 years was a number amenable to harmonic analysis (involving only the three lowest primes—2, 3, and 5). Such an ideal number is called canonical.
It has long been held that the period between Jupiter and Saturn conjunctions, called the Trigon period, was the natural subdivider of precession, even though the evidence appears weak when aiming for the figure of 2,160 years for an age and 25,920 years for the full precessional cycle. Platonic assumptions aside, the Trigon period’s duration, 19.859 years, is 16/15 of the lunar nodal period of 18.618 years. The Trigon period is therefore related to both the modern estimate for precession and the moon’s nodal period through its relation of 15/16 to the Trigon period.
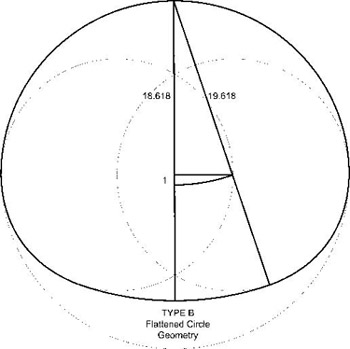
Figure 2.13. The Type B–flattened circle is a geometry generated by dividing the circle’s diameter into three parts. The lower semicircle is then replaced by arcs radiating from these centers and, between these, by a diameter arc that joins them. The triangle formed by the arc between the two inner centers is the right-angled triangle for the nodal period, as in figure 2.14, a fact realized by Robin Heath as proof that Megalithic astronomers investigated the nodal period geometrically, once they had elucidated this ratio as a triangular form.
The Trigon period can therefore be viewed as the natural type of minute for the clock face of the Great Year—and its 12 signs are like the hour divisions to which the hand of the precessional present moment points; making the modern clock face is a perfect metaphor for precession. There are 108 Trigon periods in an equinox age, which is a canonical number (9 × 12) traditionally associated with the moon.
The moon, key to stabilizing Earth’s precession, is therefore found to have its eclipse and nodal behavior tied to the Trigon period, and thus the two outermost, visible planets. This gives the terrestrial precessional cycle a highly accurate synchronization to the moon, Jupiter, and Saturn; and these are the most gravitationally influential forces upon precession apart from the sun and hence the solar year. It is also true that Saturn has a synodic period of 16/15 lunar years, the same as the Trigon period’s relation to the lunar nodal period. Jupiter’s synodic period is also synchronous with the lunar year, but in a whole tone of 9/8 (with a unit of 3/2 lunar months; half and whole tones are explained in the following chapter), whereas there are 17 Jupiter synods in the moon’s nodal period plus an additional 18.618 tropical days. At Carnac, the eastern cromlech displays this ratio of 15 to 16 between its forming circle and the outer, egg-shaped perimeter, indicating that this ratio between the nodal period and the Trigon was quantified through the megalithic astronomical work of the famous Le Menec Alignments.
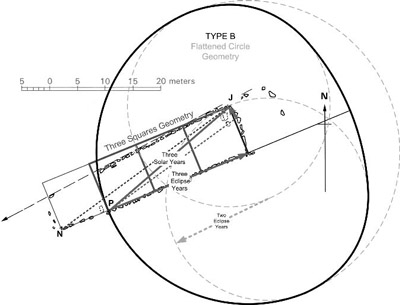
Figure 2.14. Type B geometry in the context of Le Manio’s Quadrilateral. The eclipse to solar year triangle can be constructed using the diagonal of three squares just as the soli-lunar triangle can be constructed using the diagonal of four squares, implying a geometrical simplicity behind astronomical time. This construction can be seen within the Quadrilateral if three eclipse years, in day-inches, are taken as the baseline from the sun gate and three solar years are raised upward. This suggests how the type B–flattened circle geometries were actually built using three squares, which then became another portable technology—like the four squares geometry—for Megalithic circle builders.
As an aside: the precessional cycle of 25,740 can be factorized in an interesting way as 99 times 260 years. The Tzolkin Mayan calendar is 260 days long and if multiplied by the 365-day Haab, a Mayan solar calendar, would generate a full cycle between these calendars that is 260 practical years long. The 99 periods of 260 years then point to 25,740 years, whereas 100 such periods would equal the familiar 26,000 years often used as a first approximation of the precessional period. There is a reference in Islam to the 99 names of Allah, the hundredth of which is unknowable, and this would be a typical way of encrypting a sacred fact in the biblical/Semitic tradition, as with the biblical allusions to the square root of two and doubling the volume of a cube, which I discuss in the next chapter.
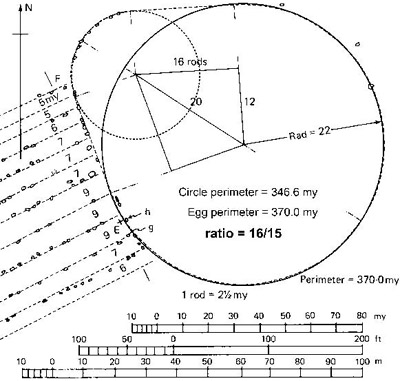
Figure 2.15. The eastern cromlech of the Le Menec alignments displays the 15 to 16 ratio between the moon’s nodal period and the Trigon period of Jupiter-Saturn conjunctions. The implication is that this link between the moon and the Trigon could have been identified, the Trigon then being the traditional subdivisor of the precessional cycle of 25,740 years.
NUMERICAL SYMBOLS OF COSMIC TIME
Ratios manifesting as numbers and geometries emanated from the Megalithic study of cosmic cycles, and this generated a new class of number symbolism that contrasted with the metaphoric symbols developed by the earlier storytelling age. These numerical symbols were related to the characterization of planetary gods, and they extended beyond the simpler categories of twofold, threefold, and fourfold divisions already obvious in the sky—found in the Northern and Southern Hemispheres; the Equatorial, ecliptic, and galactic frames; and the four gates of the sun throughout the year. Seven already represents the number of planets (5), including sun and moon (2), and the two extra nodal points in which eclipses occur, to make 9 moving factors.
The Megalithic activity expanded the range of characteristic numbers that were symbolic for the bodies that generated them, using the day-count triangles they built. These first became significant through astronomy but then became a basis for sacred symbolism involving number. This became our sacred, religious symbolism but then was obscure, rather than intelligible, in its codification of the cosmic facts.
Five for Venus, the Goddess
Venus is the brightest object in the sky besides the sun and moon. It is at its brightest when it approaches and departs from Earth in a cycle that takes 584 days. The solar year, in practical terms, is 365 days, and the common unit of time between these two periods is an accurate 73 days, of which there are 5 in the practical year and 8 in the Venus synodic period. As a consequence, there are 8 Earth years in 5 Venus periods, which means that the manifestations of Venus, such as an evening star or as a morning star, appear again within the zodiac in a position moved on from the last by 2/5 of the zodiac. In 8 years, a pentangle is described by, for example, the morning star in the heavens, and therefore Venus is most strongly associated with the number 5 and with the 5-sided star.
At the root of 5 lies the golden mean, a touchstone ratio for use in architecture, most notably that found in ancient temples, especially Greek or Roman, or in modern styles that borrow these classical styles. Venus was said to be the cosmic generative principle cut away from the sky god by Saturn, the god of time.
Seven for Saturn, the God of Time
The synodic period of Saturn is 378 days, which divides by 7, making the 7-day week commensurate with Saturn’s synod of 54 weeks. The 52 weeks familiar as our year is not exact, because 52 × 7 = 364 days, and this causes the daily movement of dates, such as birthdays, every year. Yet this Saturnian year of 364 days was widely observed in the pagan world, working with exactly 52 weeks or 13 months of 28 days, and was associated with a matriarchy that elevated men as kings who ruled for a year and a day—that is, a solar year of 365 days. It was thought that these kings eventually took over, to create patriarchal societies with the Olympic sky gods who have come to dominate the West. The leader of the Olympiads was Jupiter, who had displaced Saturn and the original Titans that operated the mill.
Twelve and 60 for Jupiter, the King of the Gods
Jupiter is titled King of the Gods, and he stands for the perfect numbers, such as 12, based on 2 and 3. Twelve times 5 is 60, and 6 times 60 comprises the perfect regularity of 360 degrees in a great circle. Though there are 12 lunar months within the solar year, forming the lunar year, the synodic period of Jupiter is 9/8 greater than this, a perfect whole tone (see next chapter). Jupiter therefore owns the moon, because the two bodies are in resonant interlock.5
If the moon is a key part of the mill, then Jupiter holds the handle with his whole tone. Yet Saturn is to be found behind him, since Saturn has a semitone relationship to the moon, and the Jupiter-Saturn Trigon period is commensurate with the precessional cycle. Jupiter also sweeps out 1/12 of the zodiac in 361 days, 361 being the square of 19 leading to relations to the longer Saros and Metonic periods.
Nineteen for the Moon, the God of Measure
The whole of the moon’s essential behavior is contained in the Metonic cycle of 19 years, and the eclipse phenomena operates between 18 and 19, as the Saros period of just over 18 years (for the repetition of similar eclipses) and the lunar nodal period of 18.618 years. Nineteen bluestones at the center of Stonehenge, therefore, pointed to lunar symbolism, especially since the bluestones themselves, partly quartz, have a lunar designation.
It is extremely unlikely that the sun, moon, and stars coincide in such a short cycle and exactly on an anniversary or year end. The Saros cycle of eclipses consists of 19 eclipse years and 223 lunar months. Nineteen lunar years contain 228 lunar months (5 more months) and 19 solar years, the Metonic cycle, 235 months (7 more again) making 12 months, or one lunar year, between the length of the Saros and Metonic cycles.
The Music of the Spheres
Numerical astronomy reveals ratios, and when these were found to be particular, whole number ratios, such as 9/8 (whole tone) or 16/15 (half tone or semitone), then the planetary spheres came to be seen as having some musical content. This idea was taken to the extreme in the Age of Aries, when massive tone matrices made up of only 2, 3, and 5 were built (see chapter 3). This established a new playground we call arithmetic and abstract analytic mathematics and storytelling based upon pure harmonic facts.