GOD AS HARMONY IN ARIES
THE LITTLE-KNOWN ACHIEVEMENTS and discoveries of the Megalithic period emerged through steps involving counting and the geometrical properties of circles and triangles. Once this geometry had arisen, based on counted lengths, it developed a metrological toolkit in which types of foot measurement could perform tasks such as obtaining an integer perimeter from an integer radius by building near-Pi ratios such as 22/7. By the end of the Megalithic age, it was obvious to those that understood it that the cosmic world was an artifact built upon numbers—but what were numbers?
The answer to this question leads down a different road than that of megalith building. The constructing of temples employed sacred numbers as a norm for religions in the Age of Aries, but though these temples were large, and in some cases aligned to the heavens, these temples did not focus outward: they sought to create religious spaces for the gods. Neither did these interior spaces marshal the dead for an afterlife, as burial mounds had.
This was a world torn asunder by Iron Age conflict, with gods having the power to bestow victory or defeat. Civilization, unified by the trade but riven by conflict, had been established in the Bronze Age—and only trade could make fortunes and create empires, dynasties, and great cities. The emerging numeric and arithmetic skills became as important in the measurement of trade goods and debts as they were to the new abstract abilities of astronomers who, instead of constructing megaliths and building proportional calculators, made tables of measurements, developed numerical shortcuts, and calculated results. The role of numbers as a tool had changed after the Megalithic period.
What happened to the Megalithic knowledge in the recently inaugurated practice of writing history? There are few written traces of most of the results presented in chapter 2, except that a new type of quasi-secret activity began—an activity conducted by priestly scribes and focused on numerical harmony. Evidence of this has recently emerged, showing most of the surviving literature from the Age of Aries to be encoded using a very specialized knowledge of musical harmony. We also find that the metrology of the Megalithic period expanded into a larger set of standard measures, especially suited to representing musical tones and hence harmonic concepts.
In the Age of Pisces, the resulting literature—such as the Rig Veda, Homer’s epics, the Bible, and other texts, especially the stories of Semitic religions—came to affect intellectual and religious life. These stories, told as factual (hence “literal”) but largely based upon sacred numeric ideas about harmony, were a major intervention in human life. Specialists in many different regions carried out this intervention, but they were probably descendants of the specialists who, in the Age of Taurus, had discovered the secrets of the cosmic world and were now priestly scribes.
The mutation of megalithic metrology into the rational world of harmony was like a move from applied mathematics to pure mathematics: the subject became the generative power of numbers rather than their practical application, and cosmic time periods were no longer the generators of significant ratios.
FROM METROLOGY TO MUSIC
The first realization about harmony was the need to establish the mathematical constraints on what are harmonious intervals, an interval being the ratio between two notes. Early music had discovered that strings vibrated according to their length and that the harmonious intervals between notes, seen as a ratio between string lengths, were few and definite to produce harmony to the ear. The Indians suggested the universe was made of sound and therefore embodied number harmonies. Such ideas establish a link between cosmology, metrology, and the harmony found in the lengths of strings that generate sound. Metrologists were well equipped to study the mathematics of music (it is simpler than astronomy) and to take the early steps in acoustical theory. This exploration was conducted by using small musical instruments such as the monochord—a single string running over a sounding board whose vibrating length could be altered. Intervals could then be measured in terms of ratios between string lengths.
We know of a broad range of standard length measures, named after the places where they were first discovered in practical use or where they were clearly involved in the construction of local monuments. The royal cubit of 12/7 feet is, for example, based upon a foot of 8/7 feet but it is 3/2 larger. This royal unit of length is considered Egyptian and can be found throughout the dynastic Egyptian monuments. It was widely used in that region, where gods and god-kings were shown pictorially as 8/7 taller than ordinary men. The ratio of 3/2 between string lengths generates an interval called the perfect fifth, which is the most harmonious interval after that of the octave ratio of 2/1.
In fact, the most unusual thing about historic measurements is that they all have a single root since they are all fractions, or ratios, of an English foot, and these fractions are largely composed of harmonic intervals such as 9/8, 10/9, 16/15, 21/20, 25/24, and 36/35, all of which are found in Plato’s defining works from the ancient school of musical harmony. Plato wrote about the world of musical harmony in an explicit way, whereas the norm at his time was to create the harmonically encoded stories found in the scriptures and epics of the period. The underlying structure of these stories could be understood only by those initiated into these harmonic mysteries. We must be grateful to Ernest McClain who has rediscovered, in recent years, Plato’s harmonic science and hence revealed what lay behind the harmonic epics and scriptures of this Age of Aries.
Long before Plato, however, metrology appears to have been an early tool used now to explore a universe of harmony rather than the time periods of astronomy, as is clear in the harmonic fractions built into the historical measures of length. Otherwise, why should the different types of feet encompass all of the harmonic ratios?
In air sound moves in a series of compressions and rarefactions, and the distance between successive compressions is called the wavelength. The higher the pitch of the sound, or what is called the frequency, the shorter its wavelength. In a stretched string, notes are made by the string’s oscillation. Instead of the energy traveling from one place to another as in sound waves moving through the air, in a stretched string the energy is contained in what is called a standing wave. Its basic note has a wavelength of the length of the string. If this length is halved, then the frequency or pitch is doubled. The interval between these two notes is called an octave, and its two notes are often referred to as “low do” and “high do.” The number 2 creates this first harmonic fact.
In changing from one note to another, we move up or down in string length. The resulting change in pitch is called an interval. In classical “pure” tones, rather than in the compromises of modern tuning, each interval is a numerical transformation represented by a fraction in which only the numbers 2, 3, and 5 are present as the numerator and denominator, respectively. It is a miracle that just these three prime numbers can create all the intervals required to fill an octave’s doubling in frequency so as to provide the world of musical harmony.
Within the span of octave doubling, the next highest number after 2—that is 3—combines with 2 to generate the next two most harmonious intervals: the fifth (3/2) and the fourth (4/3), plus the whole tone 9/8, which is the interval between them. An ascending fifth from low do is also a descending fourth from high do. The next prime number is 5, which leads to two new intervals, another whole tone (10/9), and the semitone 16/15.
When intervals are “added,” they are in fact multiplied, because they exist within a logarithmic world (base 2 because of octave doubling). For every note there are many octaves above and below it, each of which is a doubling or halving yet each sounding the same only higher or lower. Within each octave, the same harmonic intervals are always found because each octave is always just a doubling, independent of what note is actually being doubled. One can therefore call the octave and the possible intervals within it an invariant property of the universe, and this ancient science of musical harmony, when encoded into the scriptural and epic writings, is The Myth of Invariance referred to in the title of McClain’s widely published book. (As we have seen in previous chapters, astronomy and ring composition were the myth-generating invariants from previous Ages.)
Adding the interval 10/9 to the other whole tone interval (9/8) generates a major fifth, because these two tones reduce to 5/4 when multiplied (the nines canceling leaving 10/8, which is 5/4). Harmonious intervals of this kind determine the form of what we call a scale, such as our diatonic scale with its familiar notes of low do, re, mi, fa, sol, la, ti, and high do (see figure 3.1). This form is invariant, or constant, and exists within the world of number itself though experienced directly by the ear and, in music, by the mind. These intervals can be arranged in six different sequences with regard to placement of the semitones (16/15), leading to the familiar modal music of different scales. Each scale is made up of the five whole tones and two semitones that always add up to octave doubling. (A weak cosmic parallel to this is 5 visible planets and 2 luminaries—the sun and moon—which, when added, equal 7.)
Pure tone harmony is limited in that it must provide intervals that guarantee exactly matching octave doubling. As we have said, this harmony is built using only the first three prime numbers—2, 3, and 5—and it is a fundamental tenet of musical harmony confirmed by the ear yet wholly numerical. Yet if string lengths are defined using metrology, even if the metrological system has all the requisite ratios readymade, the task is challenging. Any given length defining a note must be able to be scaled up or down to allow others to be harmonious to it. Fortunately, in going back to thinking about lengths with respect to a right-angled triangle, the triangle’s slope angle is such that any length placed on its base can be projected upward onto the hypotenuse to scale up that length by the ratio of the triangle’s longest sides. In other words, the slope angle defines a ratio that can multiply any string length and establish a new string length so as to achieve any required interval. Division by the same ratio can also be achieved by reducing a length, by projecting downward from its hypotenuse to its base, so as to increase the frequency of sound produced by a string.
The reason why our historical measures are harmonically related to the English foot becomes clear. Metrology was used to construct the string lengths within a study of harmony; using the same number of two different types of foot defines a length for the hypotenuse and base for a harmonic ratio, seen as a triangle. Originally, making harmonic measures would have involved the creation of a suitable triangle having the necessary ratio in its side lengths, measured in English feet. Once a range of such harmonic interval measures was constructed, there was no longer any need to construct triangles every time. Instead, an English measurement ruler can be used to measure a string’s length and that same number of units using a different foot would achieve the required tone’s string length. It would have been possible to build an early fretted instrument; the distance between frets marking the differing string lengths for the same string, when pressed down to the fret.
The implication is that our historic measures were survivors of metrological kits used for harmonic work and that only some of these, such as the English inch and foot, were the earliest measures used originally for megalithic astronomy. This is confirmed by the nature of the micro-variations found in historic measures that have a relation to Pi and also of our modern tuning system called equal temperament. (See An Equal-Tempered Zodiac.)
THE JOURNEY INTO HARMONIC NUMBERS
When numbers came to be notated in a written form they provided an alternative to using metrology. It was discovered that some of the whole numbers, between a starting number and double that number, were separated by the harmonic intervals found within an octave. This enabled the study of harmony using strings with whole number lengths using any unit of measure.
For example, the fifth, fourth, and whole tone intervals (involving the number 3) could be generated between the number 6 and 12 (= 2 × 6).
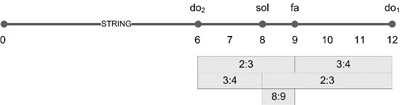
Figure 3.1. The perfect harmonic intervals provided by the integer numbers between 6 and 12
Music within a Conceptual Month
Plato used rules for inviting friends to a wedding or training guardians of a musical city to allude to the pentatonic scale formed from sets of numbers that are able to define pentatonic tuning in this way, number sets starting with 24 or 30 and therefore ending with 48 or 60. (See figure 3.2.)
It is clear that intervals involving the prime number 5 are needed to create pentatonic tuning using these numbers. However, in the scale shown above there is limited capacity available for melodic music as the intervals do not include any semitones between the pentatonic notes.
Music within a Conceptual Year
To achieve what is called just tuning, with more potential for making music, a larger starting number is required. This will enable more interesting intervals since the number of available whole numbers within the octave range has increased, and some of these will land on notes (as numbers) that are not available in a smaller octave range. The smallest number range to achieve this is 360 to 720. (See figure 3.3.)
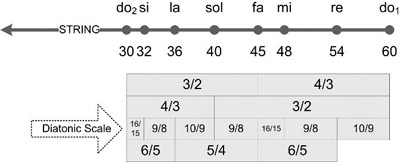
Figure 3.2. The perfect harmonic intervals provided by the integer numbers between 30 and 60. The word diatonic can be understood here as the scale of seven notes within an octave that contains two semitone intervals—a pattern seen in the white notes of a piano that, in two places, have no black notes in between.

Figure 3.3. The perfect harmonic intervals provided by the integer numbers between 360 and 720
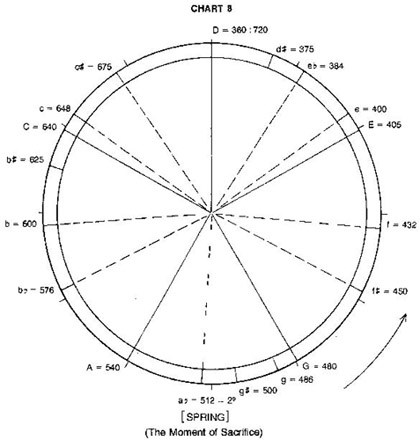
McClain says, “At this level of development, the scale ‘bent round into a circle’ as required in Timaeus (36c), can function as a zodiacal symbol. . . . Since these tones are distributed within the octave in perfect inverse symmetry, the same set of integers serves both the rising and falling scales: they could be applied to the tone circle in either direction. The 360 arithmetical subdivisions within the octave 1:2 = 360:720 correlate with the ‘idealised year of 360 days in some ancient calendars.’”1 (See figure 3.4.)
Figure 3.4. Chart 8 of McClain’s The Myth of Invariance showing the tones of 360:720 “bent round into a circle” (in a logarithmic sense) to approach a zodiacal symbol of twelve equal intervals, if a note directly below D is added. This means that twelve semitones are now available and that more than a major scale can be employed, as is found within modal music with six different permutations of the two semitones leaving five whole tones. The leading whole tone of 9/8 can be achieved using 405, shown as E, only because there are so many more integers available within the larger octave range of 360:720.
As larger integer sets are generated there is an increase in the number of harmonic intervals, and these tunings offer more sophisticated musical scales. Different starting numbers offer different sets of intervals as tuning schemes, and these appear automatically from the choice of a given starting number. While every integer ratio marks a possible interval, most of these are not harmonious within the whole octave.
The rejected numbers and notes within these harmonic intervals can be seen as sins in that they “miss the mark” set by harmony, and from this, harmony naturally emerges as an implicit value system. Such a system of values, set by an unknowable God who created the universe through numbers, is an extension of the Megalithic project concerning numbers and the cosmos. The elites of the Megalithic period doubtless became entangled in this new Age’s preoccupation with harmonic numbers, where such calculations led the way to founding new religious doctrines based on the bedrock of harmonic number and the vision of a divine harmony.
In the minds of number technicians the new harmonic realities became self-evident, but to a population of Iron Age traders, there were more pressing, everyday concerns to keep them occupied, such as trade. The two focuses coincided, and while trade had revolutionized the ancient world, popular ideas of the sacred were still embodied in the people’s stories. The power of stories is that within each successful story lies an implicit worldview and, within that, a “big issue” or moral quandary that had to be resolved. The world of harmony appeared to generate tuning systems that showed a fight between good intervals and bad intervals, where good meant the greatest harmony and bad was represented by intervals that interfered with the orderly flow of the octave and had to be overcome or redeemed. This was an implicit worldview for a story within harmony but, to reach the public ear, the narrative could not reveal itself as based on numbers.
A way forward emerged in which different cultural groups would create their own stories based on characters and scenarios drawn from different tuning systems. The starting numbers and hence tuning systems inspiring the Bible were different from those used by Homer (13,500 lines in the original Iliad), while those of the Hindus were extremely ambitious in their use of very large numbers, such as their number for world Ages (units of 432,000 “years”). However, as the numbers increased in size, it was hard to see the significance of what was really happening between them; this research program, based on finding the tunings possible using starting numbers for the octave, rapidly exceeded the acoustic world of music as experienced through musical instruments. An intellectual “space race” ensued—carried on for millennia and leaving our oldest books as its harmonically coded documents.
CLIMBING GOD’S MOUNTAIN
The number 2 is not the cause of these new worlds of intervals, as starting numbers increased, because any number doubled only forms an octave interval. How could one tell which starting numbers were good to try? The purest harmonic tones belong to integers that differ only by 2:3:4:5:6, and if 2 and 4 are removed from this list then the prime numbers 3 and 5 are the creators of harmonic intervals within octaves. Higher starting numbers unlock new interval ratios by using powers of 3 and 5 to make up the new whole number tones.
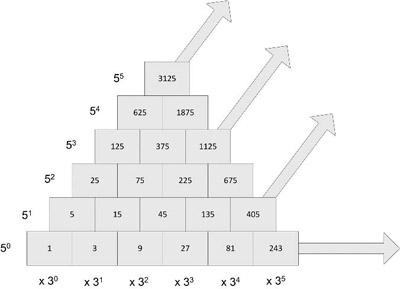
According to McClain, the musical number theorists created a grid of all these powers of 3 and 5 in which the columns were increasing powers of 3 and the rows upward were increasing powers of 5. (See figure 3.5.) A general-purpose grid was calculated covering ever higher powers of 3 and 5 and their products. It was a work that needed to be done only once in each scribal center, with the results saved in the number notation of that place and made available to fellow workers.
Step 1: Limit the Powers of 3 and 5
Using the grid of the powers of 3 and 5: what about the limiting number of 60 used for the pentatonic scale? The process is shown in figure 3.6, and it yields the same set of numbers but this time automatically—that is, using only the power grid of 3 and 5. (The grid is skewed right to show the two types of third, major and minor, as triangular relations within the grid—a technique that also proved visually evocative.)
Figure 3.5. The powers of 3 run left to right, and the powers of 5 run from bottom to top, to form the essential ingredients for any intervals within an octave. The building blocks are each the product of 3p (to the power p) and 5q (to the power q), and, because any number to the power 0 equals 1, the grid starts with 30 × 50 = 1 on the bottom left, as shown, for most of the ancient schools of harmony.
Step 2: To the Limit, Double the Numbers that Remain
Once the active ingredients for any possible harmonic interval, the powers of 3 and 5, have been limited (here, to 60, giving 45 as the highest number), how can an octave be found within the grid? The number 2, required for octave doubling, is as yet wholly absent within these powers of 3 and 5. The next key concept (see figure 3.6) was to again enforce the limiting number, but this time for every number. Each number can be multiplied by 2 the number of times that prevents it from exceeding the chosen limit (in this case 60), and then all the integers in the grid will belong only to a single octave range for that limiting number as high do. That is, all the numbers are doubled until another doubling would exceed 60, so 30 would qualify for doubling but no number higher than 30. This was probably the world’s first computational algorithm.
The shape of McClain’s yantras often resembles a mountain when the limiting number reached at the top is a pure power of 5; because each layer below employs a lower power of 5, and hence requires additional powers of 3 to achieve the limiting number, the base of the yantra is widened into the form of a “mountain.” The simplest yantra of all, shown in figure 3.6, expresses all the combinations of 3p x 5q = 60, for all values of p and q. The yantras tell of the type of gods evolved in the post-Megalithic period—gods with numeric properties that belonged to the harmonic project.
In this yantra for 60, the mean position is 22 x 3 x 5 = 60 and is associated with Anu-An, who is the god of that yantra and represents do1:do2 as 30:60. The highest power of 5 is its square, 2 x 52 = 50, traditionally the number for the god Bel-Enlil. The lesser power in the middle row is associated with the god Ea-Enki whose number is 40 and whose position is in the middle row, left, with the formula 23 x 5 = 40.
The methodology of working within numerical limits is defining a religious pantheon of numerical gods. From this view there flowed many innovations, such as using 60 as a harmonic base for the Babylonian number system, the use of 360 degrees, and a system for dealing with the arithmetic of doubling and the ability to generate ever-larger yantras.
The God on the Mountain diagram produces the lowest set of numbers that can generate a useful scale. Yet it also introduces a new meaning in which the relativity of all tones can be known from the fact that
- traveling right generates a rising fifth (i.e., multiply by 3/2)
- traveling upward and left to right generates minor thirds (multiply by 6/5)
- traveling upward and right to left generates major thirds (multiply by 5/4)
- reversing these directions generates reciprocal results
- string lengths are the inverse of string frequencies
Figure 3.6. McClain’s rediscovered method of investigating the pure tone intervals within any integer range, here presenting the range 30 to 60. In step one (starting from the bottom of the image and working your way up to the “top of the mountain”) the reader will see the top brick is five squared (25) and the middle brick is three times five (15), showing the blending of powers of three and five within the wall. All these numbers are doubled until a further doubling would exceed the limit of 60. The full scale of intervals is then available as integers, and they are guaranteed to express harmonic intervals between them. The design is similar to those yantras still drawn in India (e.g., the Sri Yantra; yantra is the Sanskrit word for “instrument” or “machine”), and the diatonic scale was the one seen previously for 30:60.
The God on the Mountain outline is evocative, as are the directionality and tonal characteristics that generate a tonal topography for storytelling. This was seized upon in order to write scriptures. New types of scripture from the Sumerian experience onward appear to use the tonal yantra as a template for the codification of spiritual myth making. This continued through the Bible’s Old Testament (Hebrew Scriptures) to the end of the New Testament (Christian Scriptures) and in the Book of Revelation. The New Testament was heavily influenced by the numerical knowledge of the harmonic schools, knowledge that Plato had made somewhat public in explicit form in his allegories about different cities: the Greeks were everywhere in the eastern Mediterranean at the time of Christ, and the harmonic initiates were amongst them. Different scriptures and epics introduced different limiting numbers and then portrayed the tonal drama unique to each, as an inspiration for the characters and dramas involved.
The power of the yantra system was that a whole set of tuning issues could be stated as this single limiting number, mentioned once or twice within a text, and anyone knowing this system could reconstruct the yantra and read the remaining text and its characterization of people, situations, and other numerical clues—a process of decoding the texts repeated by McClain in our time. The technique preserved harmonic knowledge as sacred stories in the Age of Aries.
THE HARMONIC LIMIT FOR PRECESSION
The precession cycle itself can form a yantra, which McClain provides in The Myth of Invariance.2 The Platonic Year is a precessional period chosen as being numerically suited, in length of years, to harmonic factorization (being factored only by the numbers 2 and 3). McClain has investigated the limiting number of 25,920 and created a yantra for it that reveals the harmonic intervals between a low do of 12,960 and a hi do of 25,920. (See figure 3.7.)
In figure 3.7, apart from the seven capitalized notes of the diatonic octave, available through the 30:60 octave, the elements constitute a system for the limited key changing possible within a just tuning system. In this octave of precession, the only ratios lying between its notes are just four semitones, and these prove significant to later ideas about the moon and precession and the syntonic comma of 81/80.
- the Pythagorean semitone of 256/243, which corresponds to the ratio of the Metonic period to the Saros period
- the diatonic semitone of 16/15, found between the Trigon period (that divides into the precessional period) and the moon’s nodal period (and also Saturn’s synodic period, relative to the lunar year)
- the chromatic semitone of 25/24
- the syntonic comma of 81/80, which can transpose between 5-tone (pentatonic) and just tuning and which releases the diatonic scale from some of its limitations, for example 256/243 is 81/80 shorter than 16/15
- the ratio 27/25, achieved by combining 16/15 and 81/80, which is found in the ratio of lunar month to lunar orbit
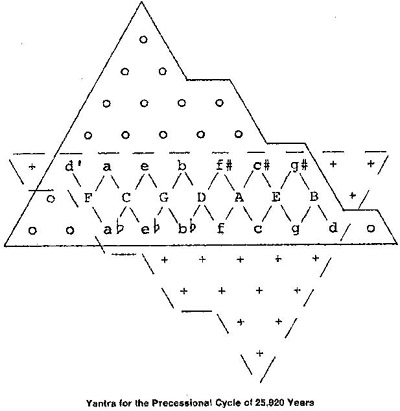
Figure 3.7. The tonal yantra resulting from a limiting number (do2) for the precessional period taken to be 25,920 years long (from McClain’s The Myth of Invariance). The mountain shape is inverted as a dotted outline in larger yantras such as this, relative to the “lynch pin” of D, the do1:do2 octave: notes contained within both mountain outlines are then relevant to both falling and rising octaves, representing reciprocal “twin” notes that are symmetrical to left and right of the tone-mandala (figure 3.8) for the yantra.
The semitones that appear with this yantra are therefore a synthesis of the tuning systems for 6:12, 30:60, and 360:720—the systems of the conceptual zodiac, month, and year within the harmonic world. These tuning systems are present in the limiting number of precession by virtue of the fact that, in an octave that ends with a high do numbering 25,920 there is a rich combination of just these possible intervals.
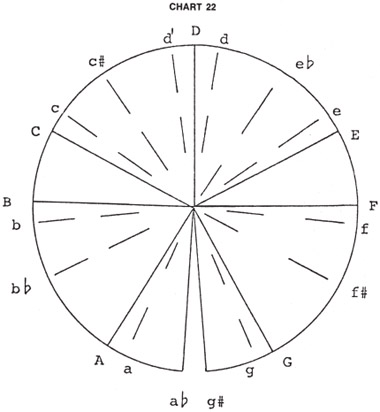
Figure 3.8. Chart 22 of McClain’s The Myth of Invariance showing a logarithmic mandala, base 2. Precession has a duration of about 25,920 solar years, which can be viewed as a frequency. This limiting number is then generating a set of intervals for the Earth. Precession, through this number, would contain definite intervals within it, with the years in a precessional cycle as high do and half of this a low do.
Chapter 6 gives further insight, based on the tones 256/243 and 27/25, which accurately define the ratios of the Saros cycle to the Metonic cycle and lunar orbital period to lunar month, discussed by the end of chapter 2. The ratio 81/80 can also be correlated to the claim that the moon affects life on Earth, which implies that the earth-moonsun system is organized to generate tones that extend Gurdjieff’s proposal of a cosmic tuning system. (See chapter 5.)
THE ADVENT OF A SINGLE GOD
Hundreds of years before Christianity and Islam arose, the Bible’s Old Testament was written using harmonic ideas such as purity, pure order, and an invisible and jealous God. But the general population had neither the time nor the inclination to worship such a God directly, because the cosmic mystery of Earth had been the substratum of the Megalithic period, when the gods were clearly in the sky. However, civilization was becoming an ideal of social order beneath god and king or emperor, according to ordering principles of rulership. Those who thought differently became pagans for the Romans who understood the Platonic ideals of state organization based upon harmonic concepts.
The work on harmony had transmitted to the mind something more powerful than beliefs, something that organized thought itself for the rational mind. This mind’s cultured education became the discriminator against the uneducated, whose identification with the land, ancestors, and mysteries disordered the objectives of the state or empire, in which controls were necessary. A harmonic parcel bomb had been loaded into scripture by adepts and would explode to create our history and the great Western religions.
On one level, the topography of a tonal matrix seems an unpromising start for scriptural content, though in retrospect it has been effective. Therefore, we must consider the possibility that these gods of harmony were indeed an effectual and powerful matrix for the mind, perhaps none other that the newly rational mind of humans, which was seeking its own order. This was not the demiurgic mind, the numeric intelligence ordering the local cosmos and now considered regressive. The rejection of the many gods, clearly based on the planetary reality, was a rejection of the earlier mind’s interest in the cosmic machine as a source of knowledge. The new mind machine could and would generate ever more information and knowledge under a god of pure symmetry and mental relativism; and categories of relevance emerged, all of these being tonal concepts.
In breaking free from the cosmic order by the end of the Age of Aries, the mind had become conscious of itself and was given new powers to think outside the box of cosmic actuality. Our modern ideal of free speech would horrify the ancient priests, whose purpose in articulation was the transmission of objective knowledge. These mores existed as late as the last great Welsh bards, whose objective poetic formulations were said to carry the power of life or death. In the New World such magical power was regressive, because all was to be held together by the mind rather than by the magical order of the natural world. This schism is fundamental to this day, and it has been continued by our modern science that explores the natural order while still not recognizing the Megalithic achievements. Within the last six thousand years, the probable sequence was:
- the mind itself came to Earth from the gods, through the numbers in the sky
- the priests and prophets revealed the one god of the mind’s harmony through the musical harmony that forms the heart of the number field.
In this way, the mind realized itself first through the sky and then through harmonic number field and became conscious of itself. By the time of the rise of Athens, humans within classical culture had started to become individual, a process called in psychology individuation.
The form of musical scale we use today is the equal-tempered scale. Its capabilities express well the new mind’s freedom of movement, allowing us to change key and to thereby play between alternative keys (different octaves, separated by a musical interval). This equal-tempered possibility was alluded to in ancient harmonic theory and was approximated as the constitution of one of Plato’s city-states called Magnesia.
The equal-tempered scale divides the whole of the octave into twelve equally increasing semitones, and in the outer world, this scale is echoed in the division of the sun’s path within the year, as it is seen as passing through twelve equal sectors called the zodiac. The Vedas seem to refer to it as:
Twelve spokes, one wheel, navels three.
Who can comprehend this?
On it are placed together three hundred and sixty like pegs;
They shake not in the least.3
To divide an octave into twelve equal semitones, we must find the twelfth root of 2, the octave doubling. We can use a calculator to reach this value—1.059—but such calculators belong to very recent times. Achieving this value is not the only challenge, as one must develop the full scale of these twelve notes, and these values are not available through the numerical yantras for any limiting number.
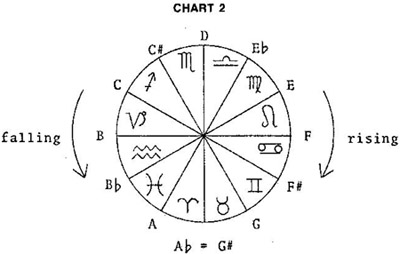
This twelfth root of 2 could only have been generated, if at all, through the Megalithic geometry of the N : N + 1 triangle, because these triangles can simulate growth based upon any logarithmic base, and the logarithm (base 2) of the twelfth root of two is numerically 1/12. It is this interval that, in an equal-tempered “zodiac” of tones, can form a tone circle divided into a “wheel” with “twelve spokes,” each equally spaced. (See figure 3.9.)
Figure 3.9. Chart 2 of McClain’s The Myth of Invariance showing a logarithmic mandala, base 2, of the zodiac as an equal-tempered scale.
If the base of an N : N + 1 triangle is given the conceptual value of 1, then there must be a value for N such that the N + 1 hypotenuse equals the twelfth root of 2 relative to the base. Furthermore, once this triangle is constructed, then N + 1 can be arced down to the base and then raised as a perpendicular to strike an extended hypotenuse at the point (N + 1) times (N + 1)—that is, an equal-tempered whole tone of two semitones.
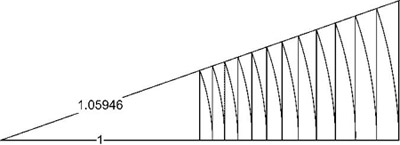
Figure 3.10. An N : N + 1 right-angled triangle that can generate the twelfth root of 2, suitable for the equal-tempered scale. The pattern of frets on a guitar are identically spaced to the lengths generated by this triangle.
We can then see that the successive applications of the same procedure result in dividing the range 1:2 into twelve equally growing intervals. What we now must determine is the value of N that can give access to this capability in order to generate an equal-tempered scale.
The triangle’s sides are close to 1/17 different and are therefore close to the 16/15 pure half tone but are a little more distant from the septenary half tone of 15/14. However, 15/14 (= 1.07142857) is different from 12√2 to one part in 175 (one of the metrological “tweaks” found in historical measures). If 15/14 is reduced by (175/176)2, then the hypotenuse becomes 1.059287, which is within one part in 6,044 of 12√2. This ratio, 176/175, is a variation found in ancient measures.
Another problem of the ancient world points us to the equal-tempered semitone: How can the volume of the cubit altar of Apollo be doubled? Today, it is known that a perfect solution to this question is impossible; however, the answer can be found in rational terms by applying an approximation to the four equal-tempered semitones.*6
By multiplying the cube’s side length by 5/4, the major third, but enlarged by 126/125, one can double the volume of a cube. This is a formula found in metrology, music, and myth. McClain says, “Surprisingly, the ‘cube root of 2’ correction of 1/125 for 5/4 probably was known in the 3rd millennium BCE stories of Gilgamesh.”4 This same correcting ratio was known in ancient metrology by both its known adjustments (176/175) × (441/440) = (126/125); that is, 1 part in 125, and its accuracy in doubling the cubic altar is just 1 part in 16,000—well beyond the accuracy of any practical metrology.
Returning to the N : N + 1 triangle that generates the twelfth root of 2, we can ask: What is the height of its third side? It is close to 7/20. If we scale the triangle to a base of 20 units, then the height is 7 units, which gives us a very simple way to arrange such a triangle in practice: we can construct a 20-unit base and can raise a 7-unit perpendicular. The resulting hypotenuse is 20 × 12√2. Alternatively and conceptually, if a metrological “step” of 2.5 royal feet is used for the base, 5/2 × 8/7 feet = 20/7 feet, whereupon the perpendicular (third) side is 7/7 = 1 English foot.*7
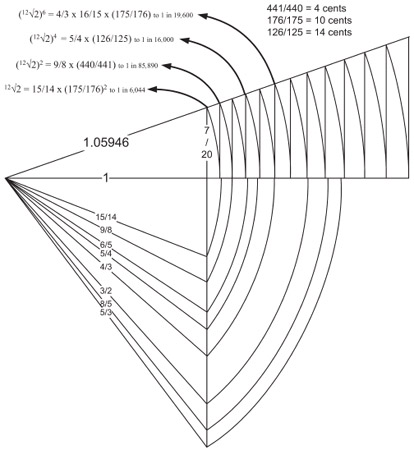
Figure 3.11. The rational intervals, and the triangles that generate them, can be compared to their equivalent, equal-tempered tones to reveal the metrological tweaks found in historical metrology. These would evidently have had a strong application in their use within harmonic constructions. (There are 1,200 cents in an octave within the system used by modern musicologists.)
We can then see the likely application of geometric metrology, its shortcuts and adjustments, could have made the equal-tempered scale available long before the modern scheme of logarithms came into existence. N : N + 1 triangles not only enabled the capture of essentially logarithmic ratios in celestial time periods, but also provided the logarithmic calculations required by musical mandalas in the round, because the iteration of such triangles inherently lead to logarithmic growth measures. Though such logarithms might not seem accurate, higher accuracies are always available to the builders of larger versions of such triangular calculators, whereas relatively small triangles deliver the accuracy necessary for acoustic comparison to the pure-tone scales.
THE IMPACT ON HISTORY
The numerical encoding of scripture translated the objective speculations arising in the Megalithic period, into a world of literary allusion that became the classical foundations of our civilization. If one had no knowledge of what these scriptures alluded to, then they appeared to have only mythic content, which generated the familiar interpretation of scripture found in the major monotheistic religions: Jewish, Christian, and Islamic.
Octave doubling and tonal experimentation presents the idea that the world is organized by the invariant pattern of the harmonic number field. An octave carries a sense of transformative achievement through the intervals within it that makes new types of plot and characterization possible, outside a musical context and inside a literary one.
The innovation of this new style of storytelling, in the Age of Aries, displaced the numeric realities encoding the structure of the sky. Though the harmonic technicians tried to reconcile the sky to musical harmony, their attempts could find no ideal reconciliation between the cosmic and the harmonic. They found only annoying similarities, themselves remarkable: 365 days were like the 360 degrees of Babylon and the 360 pegs that generate a conceptual calendrical tuning system. (Where 360 is 5 times 72, and 365 is 5 times 73.)
The realization that stories could not only be tonal but also have a circular form might have been the inspiration for the compositional structure evident in the Bible’s Pentateuch and later literary works. The fact that ring (or circular) compositional structure has been found to run parallel to the harmonic encoding of documents such as Homer’s Iliad means that the writers understood both structural and harmonic principles and reverenced both of these literary skill sets. It was probably thought that stories should embody a number of compatible and harmonious steps so that they should return to where they started, though at a higher point (the octave doubling of harmonic theory paralleling the latch of circular composition).
In the rise of post-classical cultures there was an ignorance of these harmonic and structural literary disciplines and their use in the older scriptures and epics. There was a corresponding drift toward religious dogmatism and a theology based upon scriptural “facts” that supposed such works to be the literal word of God or actual historical events. The growing sense of individualized thinking, which we call rationality, would be suppressed by the convenient dogmatism that God fancied himself as a writer rather than being the creator of a universe in which the structure of the cosmos and of musical harmony had led people to write about Him. Ultimately, a rational science would designate all the past systems of thought as merely of historical interest.
The mind machine of human thought ultimately replaced the study of a cosmic machine ordered according to number. This mind machine is based upon subliminal elements from the past—works that survived from antiquity and capabilities that had been won through the previous precessional ages. Since the Middle Ages the growth of the mind machine has been exponential due to new technologies.
However the cosmic and harmonic study projects did not come to an end. Secret groups continued to preserve and evolve secrets about the environmental and inner life of mankind. A harmonic cosmology emerged from a Central Asian group called the Sarmoun Brotherhood through the writings of G. I. Gurdjieff before World War I. As we will see in chapters 5 and 6, this emergence unifies the otherwise incompatible views of the cosmic environment and the harmonic theories of chapters 2 and 3.