3

THE DIRECTIONALITY OF LOGIC

DOES BEING HAPPY MAKE YOU EAT CHOCOLATE?

EATING CHOCOLATE MAKES ME HAPPY instantly. It has to be good chocolate, but it works without fail every time.

Does being happy make me eat chocolate? That’s a completely different question.

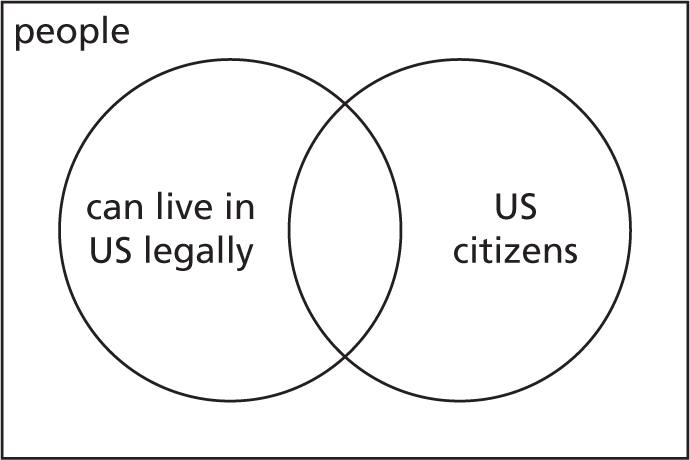
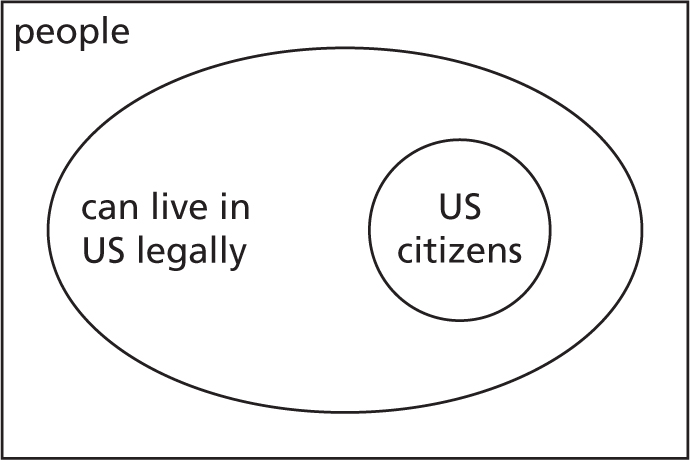
On a more serious note, being a US citizen means that you can legally live in the US. If you can legally live in the US, does that necessarily mean you are a US citizen? This is a completely different question. Some people erroneously think that being a citizen is the only way to be legally resident, but there are plenty of other ways, including having a work visa, permanent residency, or being admitted as a refugee.

Time and causation flow in one direction only, and so does logic, and we must be careful not to make errors in direction. In the last chapter we described the string of swaps Kyle MacDonald made, starting with a paper clip and ending up with a house. I sometimes wonder if these swaps were reversible. If he changed his mind about, say, the snow globe, would the original owner have taken the item back? It’s not clear.

In the example in the previous chapter, I argued that if you don’t stand up for minorities who are being harassed then you are almost as bad as an outright bigot. What if we turn this round? If you are almost as bad as an outright bigot does that mean you don’t stand up for minorities who are being harassed? No, there are plenty of other ways to be “almost as bad” as a bigot even if you do stand up for harassed minorities and think that this completely exonerates you. Perhaps you stand up for them in public but then quietly block their promotions or pay rises, turn them down for jobs, or refuse to vote for them.

The point is that we have an implication like this:

not standing up for harassed minorities almost as bad as a bigot

but we can’t just reverse the arrow to get this:

almost as bad as a bigot not standing up for harassed minorities

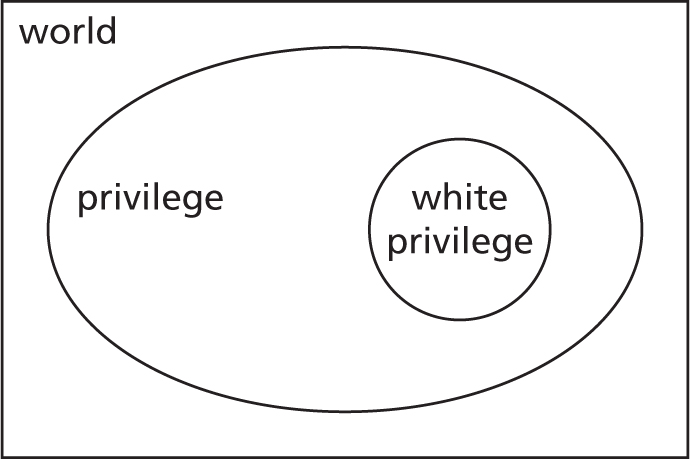
The fact that the implication sign looks like an arrow is not a coincidence. It is chosen to help us see that the logic flows in one direction only. Turning the arrow around would change the meaning, possibly drastically. Take the logical privilege example from the previous chapter. In the original form it was

you have white privilege you have privilege

If we turn the direction of the arrow around this becomes

you have privilege you have white privilege

This is obviously not true as there are plenty of other types of privilege that you might have even if you’re not white, such as the privilege of being born to rich or powerful parents.

What about this:

you are a woman you have experienced sexism

This is the premiss of the Everyday Sexism project: that every woman experiences sexism, even if it’s not overt. It might take the form of micro-aggressions that we’re supposed to brush off, and perhaps we’re so accustomed to it that we barely even register it any more. The sad fact that we take it for granted as a part of life doesn’t mean it’s not there–on the contrary it means that it is everywhere.

Now let’s try turning the arrow around:

you have experienced sexism you are a woman

This is a completely different question, but unfortunately often gets muddled up with the first one. If you say “all women experience sexism” someone (usually a man) is likely to protest that men experience sexism too. This may or may not be true, but in any case it is not logically related to the first question. The first implication says that if you are a woman then you have experienced sexism; it does not claim anything if you are a man.¹

All these examples show that the act of turning the arrow around in an implication statement makes a completely new statement for us to think about. The statement that we get by turning the arrow around is called the converse of the original statement.

ON BROCCOLI AND ICE CREAM

One of my favorite examples of implications and converses is “If you eat your broccoli you can have ice cream.” I will admit up front that this gets quite confusing in normal language, which is why mathematicians quickly prefer using letters and symbols to keep things clear. But let’s try with words.

A logical, literal child might start asking what other foods will imply ice cream, if they really want to avoid broccoli. Here their precision comes across as pedantry to the adult, who might say exasperatedly “You know what I mean!”, but the child is just seeking clarity and trying to find a loophole to avoid eating broccoli. (I was not that child–I have always loved broccoli. Perhaps because it was never used as a threat to me. Or maybe it was never used as a threat because I loved it.)

The child might say “How about if I eat some fish instead?” to which the answer might be “No, you have to eat your broccoli!” or “No, you get ice cream only if you eat your broccoli!” These are both examples of a converse, but it’s a bit hard to see with the broccoli example because it’s not really a logical implication–more of a bribe.

Here are the two statements the parent made. First they said

If you eat your broccoli you can have ice cream.

broccoli ice cream

which guarantees the child that broccoli leads to ice cream. It says that if the child eats broccoli that is sufficient for earning ice cream.

The parent then said

You can eat ice cream only if you eat broccoli.

ice cream broccoli

which guarantees the parent that the child can’t sit and try to find other ways of earning ice cream. It says that broccoli is necessary for earning ice cream, and there is no way round it. It is the converse of the first statement. (If the direction of this arrow looks strange, you can think of it as saying that if we subsequently see the child eating ice cream we can logically deduce that they must have eaten their broccoli.)

All this is to explain why “only if” is a way of expressing the converse of “if”–logic is flowing in the opposite direction. To ensure both the guarantee to the child and the guarantee to the parent, the promise technically needs to be “You can have ice cream if and only if you eat your broccoli”. The trouble is that probably only a rather pedantic mathematician would bother saying that, so we grow up with the vague sense that “only if” means the same as “if and only if”. Making the distinction in normal language is probably pedantic because it oversteps the goal of clarification. The trouble is that not making the distinction causes confusion for people when they do start thinking about logic formally. This can lead to much more serious consequences in more serious situations.

Imagine you’re trying to catch a group of bank robbers and you know the whole gang was white men. So you know

If someone you encounter is in that gang then they are a white man.

This is equivalent to

Someone you encounter can only be in that gang if they are a white man.

So we can start by looking for white men. But finding a white man does not ensure that we have found a criminal, because the converse isn’t true. The converse would be

If someone you encounter is a white man then they are in the gang.

Being a white man is a necessary condition for being in the gang, but not sufficient.²

All this is very prone to get confusing and make your head spin in normal language, which is one of the reasons mathematicians reduce things to letters and symbols, because it can be easier to see patterns. Using arrows we have:

• True: gang white

• False: white gang

We’ll deal with falsehood in the next chapter.

USING ARROWS TO HELP US

Mathematical notation is one of the things that can make mathematics baffling and difficult to learn. However, the notation is there to help us think clearly. Implications and converses demonstrate this. This can be extra confusing in normal language, because of the flexibility of English grammar and where we can put the word “if” in the sentence.

You can have ice cream if you eat your broccoli.

is logically the same as saying

If you eat your broccoli you can have ice cream.

In general we see that “if A is true then B is true” means the same as “B is true if A is true”. This might look like we’ve turned around the flow of logic, but we’ve actually only turned around the grammar.

One advantage of using arrow notation is that the flow of logic is completely clear from the direction of the arrow.

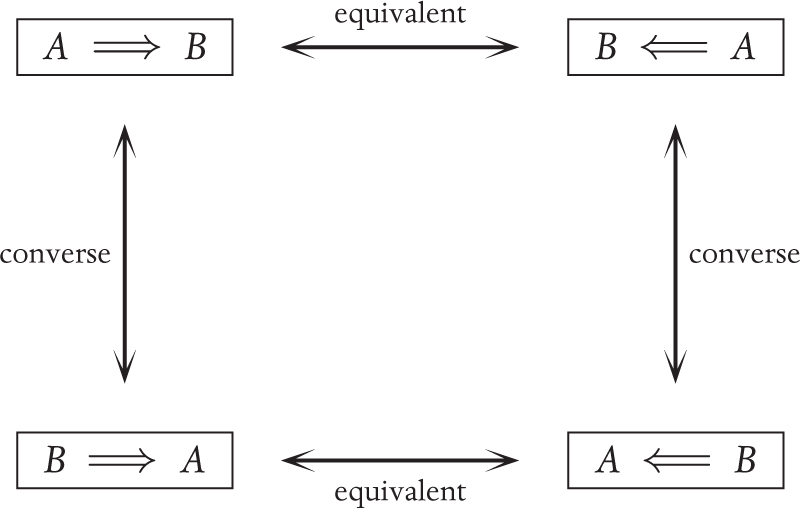
The converse of

A B

is

B A

But also

A B

is equivalent to

B A

as it doesn’t matter which way the arrow is facing on the page, only where it is pointing from and to. Indeed, we would mean the same logically (although maybe it would be a bit questionable emotionally) if we drew it like this:

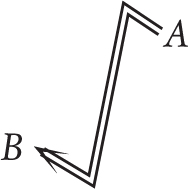
So we have these possibilities:

If we try this using if/then again, the converse of “if A then B” is “if B then A”.

The new statement looks superficially similar to the old one but is logically completely different.

USING VENN DIAGRAMS TO HELP US

Venn diagrams can help us picture some aspects of logic. I find pictures crucial when I’m doing math research. I often look like I’m staring into space, but what I’m really doing is manipulating pictures in my mind. Math gets its power from being abstract, that is, removed from the real world of objects and things we can touch. The trouble is that means it’s hard to get a feel for it. One thing that helps is having pictures that capture some aspect of what you’re thinking about. The pictures are like analogies (with apologies for the meta-analogy)–they don’t exactly represent what you’re thinking about, but they sum up some important aspect of it. They help us make the transition between the dry logic and our feelings. Tristan Needham said in his book Visual Complex Analysis:

While it often takes more imagination and effort to find a picture than to do a calculation, the picture will always reward you by bringing you nearer to the Truth.

I think that is putting it a bit too strongly–some people really prefer symbols and words to pictures. But I find pictures very helpful. Venn diagrams are quite helpful for basic situations, and in Chapter 5 (on blame and responsibility) we’ll see that when things get really complicated flow diagrams are better because they have more possibilities. Venn diagrams aren’t so useful if you have more than about three sets because they get too chopped up for our eyes to take in.

In the first instance Venn diagrams can help us to see the directionality of implications.

Let’s think about this logical implication:

If you are from England then you are from the UK.

We could draw England inside the UK abstractly like this:

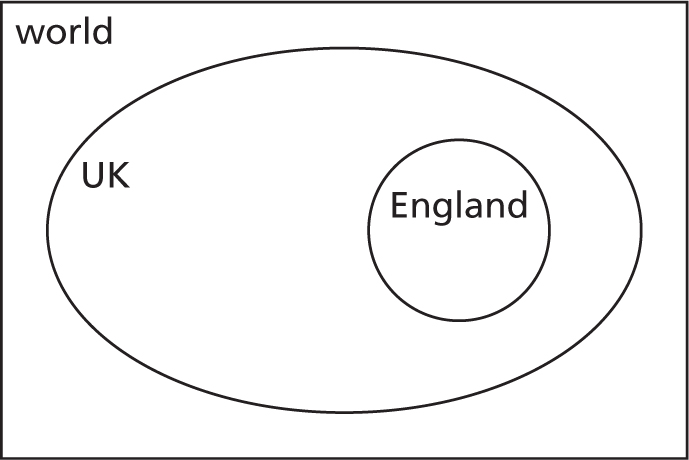
This sounds obvious but some people get upset about me saying I’m from England, because I don’t “look English”. But they don’t mind me saying I’m from the UK. Logically they must think I am in the part of the Venn diagram that is inside the UK but outside England. However, I’m not from Scotland, Wales or Northern Ireland either.³

We could draw a diagram like this for any statement of implication even if it’s not geographical and doesn’t depict physical positions. For example:

If you have white privilege then you have privilege.

If you are a US citizen then you can live in the US legally.

For the general case we have this:

A B

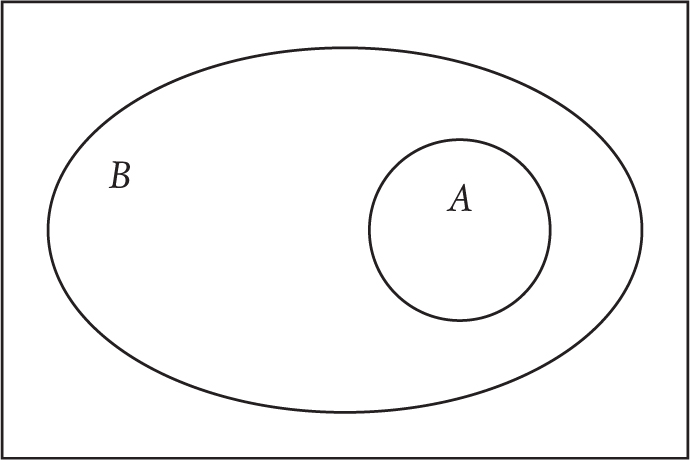
It is now a bit more vague what these circles are representing, so it is more of a schematic diagram at the moment than a rigorous one. But to me it does capture the idea that A somehow can’t escape being part of B.

The Venn diagram also makes it visually evident that the implication does not go backwards automatically, because the inner circle and the outer circle (oval) are really playing different roles. A can’t escape being part of B, but B can escape being part of A, because there is space in B around the outside of A. This corresponds to the logical fact that even if A implies B, it is still possible for B to be true when A is false. The following version is mathematically correct but misleading.

because it looks like there’s a way to be a US citizen without being allowed to live in the US legally, as well as there being ways to live there legally without being a citizen. In fact, the real situation is not symmetrical like that–the right-hand area is empty. Logical implication is not symmetrical.

OUR WONDERFULLY AND CONFUSINGLY FLEXIBLE LANGUAGE

We have seen plentiful different ways of saying the same logical implication in words. Here is a full list of different ways of saying in words

A B

including phrases putting A first and partner phrases putting B first:

• A implies B.

B is implied by A.

• If A then B.

B if A.

• A is a sufficient condition for B.

B is a necessary condition for A.

• A is true only if B is true.

Only if B is true is A true.

I think it is hard to be convinced that all eight of these statements mean the same thing, and I expect some people will write to me telling me I’ve got it wrong (so I’m checking rather carefully that I don’t have any typos). I think the last is the most confusing. Here is a tragic example.

In a chilling recent incident, a policeman in Cobb County, Georgia was caught on dashboard camera reassuring a panicky white woman that “we only shoot black people”. This is logically equivalent to saying

We shoot you only if you are black.

which is in turn equivalent to

Only if you are black do we shoot you.

or in arrows

you are black we shoot you

and equivalently

we shoot you you are black

or in words

If we shoot you then you must be black.

This is the reason that when you hear a report of someone being shot in a traffic stop in the US, you might feel fairly certain they were black.⁴

This is one reason that I prefer using symbols: it is quicker, clearer to me, and all eight of these phrases become the same, so I don’t have to use up precious brain cells thinking about what things mean.

CONVERSE ERRORS

Converse errors occur when someone makes the mistake of thinking the converse of a statement is equivalent to the statement. It’s an understandable mistake to make in a way, given that there are eight ways of saying “A implies B” and eight ways of saying the converse. This happens when you tell students that they have to work hard in order to do well, and then they think that if they work hard they should automatically do well. Working hard is a necessary but not sufficient condition for doing well. It is not sufficient because you also have to work hard in the right sort of way, and if you think otherwise you are making a converse error.

In fact, the converse of a statement is logically independent of the old statement, which means that there is no logical connection between the two. That is to say just because one of them is true, it does not necessarily mean the other one is true, nor does it necessarily mean the other one is false. In fact, all combinations of true and false are possible, as shown by the following examples:

1. If you are a US citizen then you can legally live in the US. This is a true logical implication. The converse is “if you can legally live in the US then you are a US citizen”. This is not true, as you can legally live in the US by being a permanent resident or having a visa.

2. If you have a university degree then you are intelligent. I do not believe this is true. I think there are some degrees awarded to people who are not intelligent; sadly the pass mark is very low. The converse is “if you are intelligent then you have a university degree”. This is also not true–I think there are intelligent people who do not have a university degree, especially in older generations when going to university was not such a standard next step in life.

3. If you have experienced prejudice then you are a woman. This is not true; men and gender non-binary people can experience prejudice; gender non-binary people certainly do. The converse is “if you are a woman then you have experienced prejudice”. I think this is true, whether or not you have ever acknowledged or complained about it.

4. If you support Obamacare then you support the Affordable Care Act. This is true because Obamacare is simply an informal name for the Affordable Care Act. This means that the converse is also true, “If you support the Affordable Care Act then you support Obamacare”. Unfortunately there are people who support ACA but refuse to support Obamacare, not realizing that these are the same thing. They have such a strong objection to anything to do with Obama that rebranding something with his name in it was enough to put them off. This is eye-opening, and I think we can learn important lessons from it to do with how the way we present things really does matter and can override even very clear-cut logic.

We can sum up those conclusions in this table:

	original	converse
statement 1	true	false
statement 2	false	false
statement 3	false	true
statement 4	true	true

This is all four possible combinations of true and false for the statement and its converse. This means that if we start with a new statement, discovering it is true or false doesn’t help us know anything about the converse, because it could still in theory be either true or false.

LOGICAL EQUIVALENCE

We have talked about the error of mixing up a statement and its converse, and the error of thinking that just because a statement is true its converse must also be true. However, sometimes both a statement and its converse happen to be true. In this case we have a situation of logical equivalence. That is, if A implies B and also B implies A, then A and B are logically equivalent–whenever A is true, B must be true, and also whenever A is false, B must be false.

This means that A and B are logically interchangeable, and are usually just different viewpoints on the same thing. Crucially, this doesn’t mean they’re exactly the same, as illustrated in the example of Obamacare and ACA above. Logically those are the same, but emotionally they are very different to some people, who feel fine supporting something with the calm and compassionate name “Affordable Care Act”, but can’t bear the idea of supporting something referring to Obama. Some other people have the opposite response, where the reference to Obama makes them more positively disposed towards it. We will later come back to the logical fallacy of false equivalence, where two things are assumed to be logically equivalent when they are not, such as when having a degree is taken as being equivalent to being intelligent. However, the Obama/ACA example is a case of “false inequivalence”, where some people take things to be different, when in fact they’re logically equivalent. Still, we should accept that they are not emotionally equivalent, and work with this fact rather than simply deny it on the grounds that it contradicts logic. We will come back to these issues in Chapter 15 on emotions.

When two things are logically equivalent, the implication flows in both directions, so we use this symbol: A B. In words there are several ways of saying this, and they come in symmetrical pairs as the logic flows both ways:

• A is true if and only if B is true.

B is true if and only if A is true.

• A is a necessary and sufficient condition for B.

B is a necessary and sufficient condition for A.

• A is logically equivalent to B.

B is logically equivalent to A.

• If A is true B is true, and if A is false B is false.

If B is true A is true, and if B is false A is false.

This last pair sheds some light on the fact that “A implies B” tells us nothing about the case when A is false: if we want to deduce something from A being false we need the converse although, on the face of it, the converse gives us a way to deduce something from B being true rather than from A being false. We’ll come back to this in the next chapter, in which we are going to explore what it means for things to be false.

¹ The question of whether or not men experience sexism comes down to the definition of sexism. According to some theories of prejudice, sexism and racism should only be used for instances that fit into a bigger picture of systematic oppression. The idea is that when an oppressed group is biased against their oppressors, this is not the same as when the oppressors are biased against the oppressed group as a form of control. Whether or not we agree with these definitions I think it is important to notice the difference between oppressed people and oppressors, and we will come back to this in Chapter 13 on analogies. Thinking of it in these abstract terms clears up something about the difference; giving it a name would help us think about it.

² This approach of looking for white men would make sense if you knew that the gang had five people and you also know there are exactly five white men in the country. It might even be reasonable if you know there are exactly ten white men in the country, because if you round up five of them the odds are quite high that you’ll get some of the actual criminals. This approach becomes gradually less like logic and more like racism as the country’s population of white men grows. In reality this profiling is likely to be done against nonwhite people, not white people. How big does the country or city’s population of the minority have to be before this veers from rational into racist? This is a question of gray areas that we will come back to in Chapter 12, and we have to be very careful that incremental arguments do not give us logical justifications of prejudice.

³ I recently discovered that, technically, diagrams like the ones above aren’t supposed to be called “Venn diagrams” but rather “Euler diagrams”. To qualify as a Venn diagram, it is apparently supposed to exhibit all possible logical combinations of the sets in question. The ones above don’t qualify because one circle is completely contained within the other, so there isn’t a region where you can be in the small circle without being in the big one. Of course, this is the entire point of that particular diagram. Personally I think the distinction between Venn diagrams and Euler diagrams is more like pedantry than precision, so I shall go on referring to these as Venn diagrams, especially as that term is much more well known.

⁴ Note that the logical equivalence of these statements doesn’t mean they are true and it certainly doesn’t mean they are morally justifiable. It just means that logically they mean the same thing. White people are killed by police too, including in traffic stops. The questions of whether black people are killed disproportionately and whether this is because of racism are different, much more complex questions.