Let's assume we want to find the GCD of two integers, 18 and 24. To do so, we will invoke the gcd(x,y) function, which in this case is gcd(18,24). Because 24, that is, y, is not zero, Rule 1 is not applicable here. Next, we will use Rule 2 to check whether 18%24 (x % y) is equal to 0. Because 18 cannot be divided by 24, 18 will be the remainder:
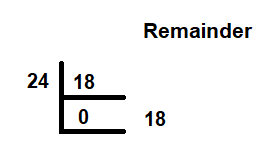
Since the parameters of Rule 2 were also not met, we will use Rule 3. We will invoke the gcd function with the gcd(b,m) argument, which is gcd(24,18%24). Now, m stands for the mod operation. At this stage, we will again apply Rule 2 and collect the remainder:

Because the result of 24%18 is a non-zero value, we will invoke the gcd function again with the gcd(b, m) argument, which is now gcd(18, 24%18), since we were left with 18 and 6 from the previous execution. We will again apply Rule 2 to this execution. When 18 is divided by 6, the remainder is 0:

At this stage, we have finally fulfilled the requirements of one of the rules, Rule 2. If you recall, Rule 2 says that if x mod y is 0, the GCD is y. Because the result of 18 mod 6 is 0, the GCD of 18 and 24 is 6.
Let's use GCC to compile the gcd.c program, as follows:
D:\CBook>gcc gcd.c -o gcd
Here is the output of the program:
D:\CBook>./gcd
Enter two numbers: 18 24
Greatest Common Divisor of 18 and 24 is 6
D:\CBook>./gcd
Enter two numbers: 9 27
Greatest Common Divisor of 9 and 27 is 9
Voilà! We've successfully found the GCD using recursion.
Now, let's move on to the next recipe!