How it works...

The two matrices are defined matA and matB of the orders 2 x 3 and 3 x 4, respectively, using the following statement:

int matA[2][3], matB[3][4]

You will be asked to enter the elements of the two matrices using the nested for loops. The elements in the matrix are entered in row-major order, in other words, all the elements of the first row are entered first, followed by all the elements of the second row, and so on.

In the nested loops, for i and for j, the outer loop, for i, represents the row and the inner loop, and for j represents the column.

While entering the elements of matrices matA and matB, the values entered in the two matrices will be assigned to the respective index locations of the two-dimensional arrays as follows:

Figure 1.10

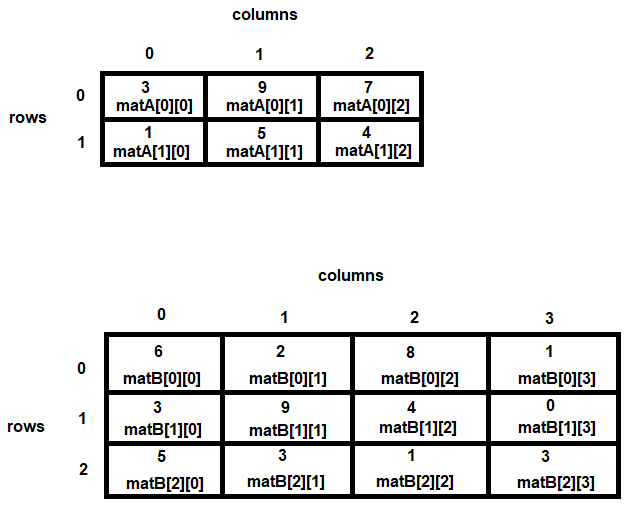
The nested loops that actually compute the matrix multiplication are as follows:

  for(i=0;i<2;i++)
  {
    for(j=0;j<4;j++)
    {
      matR[i][j]=0;
      for(k=0;k<3;k++)
      {
        matR[i][j]=matR[i][j]+matA[i][k]*matB[k][j];
      }
    }
  }

The variable i represents the row of the resultant matrix, j represents the column of the resultant matrix, and k represents the common factor. The common factor here means the column of the first matrix and the row of the second matrix.

Recall that the prerequisite for matrix multiplication is that the column of the first matrix should have the same number of rows as the second matrix. Because the respective elements have to be added after multiplication, the element has to be initialized to 0 before addition.

The following statement initializes the elements of the resultant matrix:

      matR[i][j]=0;

The for k loop inside the nested loops helps in selecting the elements in the rows of the first matrix and multiplying them by elements of the column of the second matrix:

matR[i][j]=matR[i][j]+matA[i][k]*matB[k][j];

Let's use GCC to compile the matrixmulti.c program as follows:

D:\CBook>gcc matrixmulti.c -o matrixmulti

Let's run the generated executable file, matrixmulti.exe, to see the output of the program:

D:\CBook\Chapters\1Arrays>./matrixmulti

Enter elements of the first matrix of order 2 x 3
3
9
7
1
5
4

Enter elements of the second matrix of order 3 x 4
6 2 8 1
3 9 4 0
5 3 1 3

First Matrix is
3 9 7 
1 5 4

Second Matrix is
6 2 8 1
3 9 4 0
5 3 1 3

Matrix multiplication is
80 108 67 24
41 59 32 13

Voilà! We've successfully multiplied two matrices.