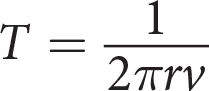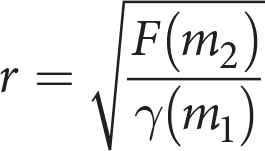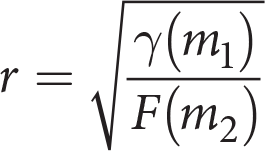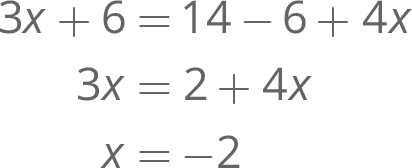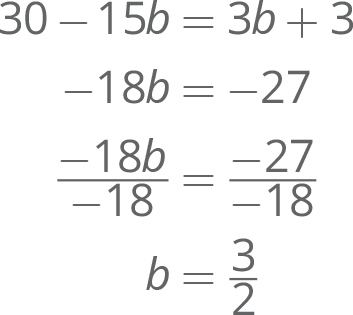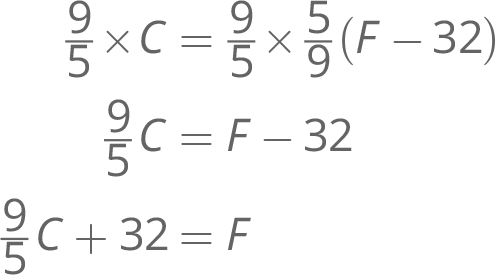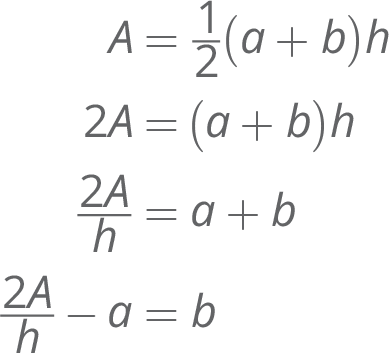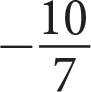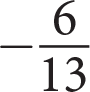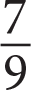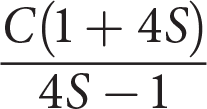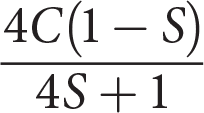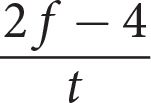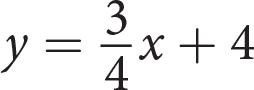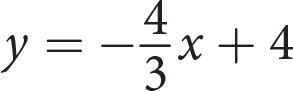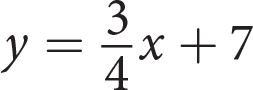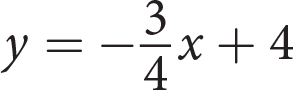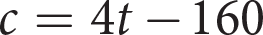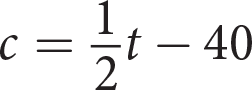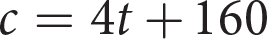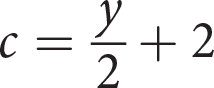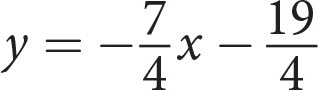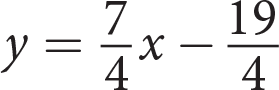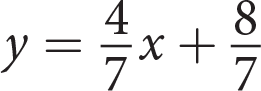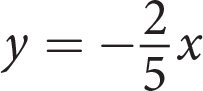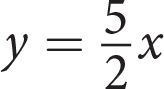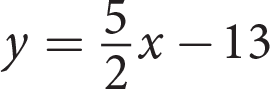Page 37

Chapter 4

Linear Equations and Graphs

Page 38

How Much Do You Know?

Directions: Try the questions that follow. Show your work so that you can compare your solutions to the ones found in the Check Your Work section immediately after this question set. The “Category” heading in the explanation for each question gives the title of the lesson that covers how to solve it. If you answered the question(s) for a given lesson correctly, and if your scratchwork looks like ours, you may be able to move quickly through that lesson. If you answered incorrectly or used a different approach, you may want to take your time on that lesson.

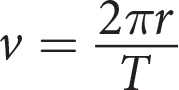
  1. Uniform circular motion is used in physics to describe the motion of an object traveling at a constant speed in a circle. The speed of the object is called tangential velocity and it can be calculated using the formula above, where r is the radius of the circle and T is the time is takes for the object to make one complete circle, called a period. Which of the following formulas could be used to find the length of one period if you know the tangential velocity and the radius of the circle?

    3.  

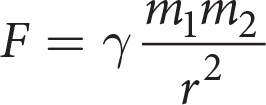
  2. The formula above is Newton’s law of universal gravitation, where F is the attractive force,  is the gravitational constant, m1 and m2 are the masses of the particles, and r is the distance between their centers of mass. Which of the following gives r in terms of F, 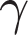, m1, and m2 ?

  3. Andrew works at a travel agency. He gets paid $120 for a day’s work, plus a bonus of $25 for each cruise he books. Which of the following equations represents the relationship between the total Andrew earns in a day, d, and the number of cruises he books, c ?

    1. c = 25d + 120
    2. c = 120d + 25
    3. d = 25c + 120
    4. d = 120c + 25

  4. Page 39Vera is on her school’s track and field team. In a practice long-jump competition against her teammates, she gets 5 points for landing over the nearer line and 10 points for landing over the more distant line. She gets a total of 7 jumps and lands x times over the more distant line and the rest of the times over the nearer line. Which of the following equations represents the relationship between Vera’s total score, y, and the number of times she lands over the more distant line, x ?

    1. y = 10x
    2. y = 5x + 35
    3. y = 10x + 5
    4. y = 70 − 5x
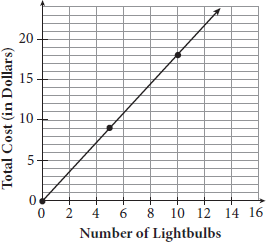
    A graph of a line with a positive slope, going through points zero comma zero, five comma nine, and ten comma eighteen. Number of light bulbs in plotted on x-axis and total cost on y-axis.

  5. A hardware store sells light bulbs in different quantities. The graph shows the cost of various quantities. According to the graph, what is the cost of a single light bulb?

    1. $0.56
    2. $1.80
    3. $2.50
    4. $3.60
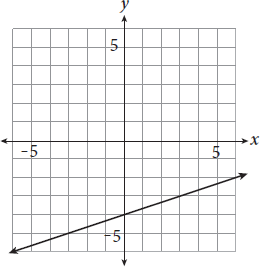
    The graph is a line that crosses the points negative 3 comma negative 5, negative four comma 0, and 3 comma negative 3.

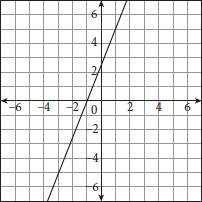
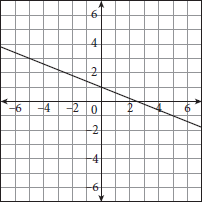
  6. The graph shown represents which of the following equations?

    1. y = −3x + 4
    4. y = 3x − 4

Page 40

Check Your Work

  1. B

    Difficulty: Easy

    Category: Solving Equations

    Getting to the Answer: The goal here is to solve the equation for T. Start by getting T out of the denominator of the fraction. To do this, multiply both sides of the equation by T, and then divide both sides by v:

    Choice (B) is the correct answer.

  2. D

    Difficulty: Medium

    Category: Solving Equations

    Strategic Advice: Even when the equation is entirely made up of variables, the process for isolating one variable is still the same.

    Getting to the Answer: This equation needs to be rearranged to solve for r, so start by multiplying both sides by r2 to get that expression out of the denominator:

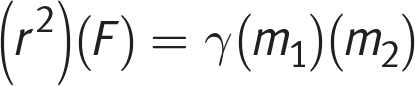
    Next, divide both sides by F:

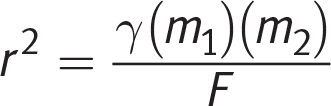
    Finally, take the square root of both sides to get r by itself:

    (D) is correct.

  3. C

    Difficulty: Easy

    Category: Word Problems

    Getting to the Answer: When writing a linear equation to represent a real-world scenario, a flat rate is a constant while a unit rate is always multiplied by the independent variable. You can identify the unit rate by looking for words like per or for each.

    Because the amount Andrew gets paid daily, $120, is a flat rate that doesn’t depend on the number of cruises he books, 120 should be the constant in the equation. This means you can eliminate (B) and (D). The question tells you to multiply $25 by the number of cruises he books, c, so the equation is total pay = 25 × number of cruises + 120, or d = 25c + 120, making (C) correct.

  4. B

    Difficulty: Hard

    Category: Word Problems

    Getting to the Answer: The key to answering this question is determining how many jumps land across each line. If Vera gets 7 jumps total and x jumps land over the more distant line, then the rest, or 7 − x, must land over the nearer line. Now, write the expression in words: points per distant line (10) times number of jumps landing over the distant line (x), plus points per near line (5) times number of jumps landing over the near line (7 − x). Next, translate the words into numbers, variables, and operations: 10x + 5(7 − x). This is not one of the answer choices, so simplify the expression by distributing the 5 and combining like terms: 10x + 5(7 − x) = 10x + 35 − 5x = 5x + 35, so the equation is y = 5x + 35. (B) is correct.

  5. Page 41B

    Difficulty: Easy

    Category: Linear Graphs

    Getting to the Answer: The x-axis represents the number of light bulbs, so find 1 on the x-axis and trace up to where it meets the graph of the line. The y-value is somewhere between $1 and $2, so the only possible correct answer choice is $1.80. (B) is correct.

    You could also find the unit rate by calculating the slope of the line using two of the points shown on the graph: the graph rises 9 units and runs 5 units from one point to the next, so the slope is , or 1.8, which confirms that (B) is correct.

  6. C

    Difficulty: Medium

    Category: Linear Graphs

    Getting to the Answer: Use the graph to identify the y-intercept and the slope of the line and then write an equation in slope-intercept form, y = mx + b. Once you have your equation, look for the answer choice that matches. The line crosses the y-axis at (0, −4) so the y-intercept, b, is −4. The line rises 1 unit for every 3 units that it runs to the right, so the slope, m, is . The equation of the line is 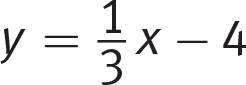, which matches (C).

    You could also graph each of the answer choices in your calculator to see which one matches the given graph, but this is not the most time-efficient strategy. You also have to be very careful when entering fractions—to graph (C), for example, you would enter (1/3)x − 4.Page 42

Solving Equations

To answer a question like this:

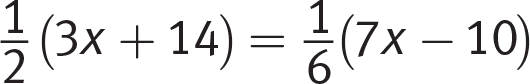
  1. Which value of x satisfies the equation above?

    1. −26
    2. 2
    3. 8
    4. 16

You need to know this:

Isolating a variable means getting that variable by itself on one side of the equation. To do this, use inverse operations to manipulate the equation, remembering that whatever you do to one side of the equation, you must do to both sides.

You need to do this:

It usually makes sense to proceed in this order: 

Explanation:

Eliminate the fractions by multiplying both sides of the equation by 6:

In order to collect all the x terms on one side, you’ll first need to distribute the 3 on the left side of the equation:

Page 43Next, subtract 7x from both sides:

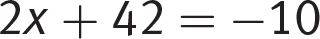
Now, subtract 42 from both sides:

Finally, divide both sides by 2 to leave x by itself:

Choice (A) is correct.

If you find isolating a variable to be challenging, try these Drill questions before proceeding to the Try on Your Own set. Isolate the variable in each equation. Turn the page and look at the bottom of the page to see the answers.

Drill

  1. 3(x + 2) = 14 − 2(3 − 2x)
  2. 5(6 − 3b) = 3b + 3
  4. Isolate F: 
  5. Isolate b:

Solving Equations Drill Answers

Page 44

Try on Your Own

Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.

3y + 2(y − 2) = 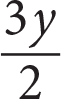 + 1

  1. What value of y satisfies the equation above?
    3.    
    4.    

  2. A teacher uses the formula above to calculate her students’ scores, S, by subtracting  of the number of questions the students answered incorrectly, I, from the number of questions they answered correctly, C, and dividing by the total number of questions. Which of the following expresses the number of questions answered incorrectly in terms of the other variables?

  3. Page 45

    What value of n satisfies the equation  ?

  1. If b ≠ 0 and 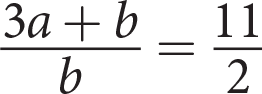, which of the following could be the value of ?

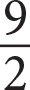
    4. It is not possible to determine a value of .

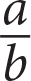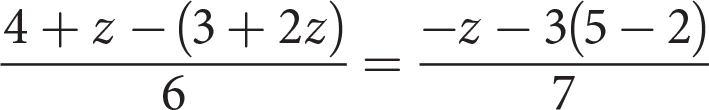
  1. What is the value of z in the equation above?

    1.   −61
    3.    
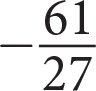
    4.     61

Page 46

Word Problems

To answer a question like this:

A laser tag arena sells two types of memberships. One package costs $325 for one year of membership with an unlimited number of visits. The second package has a $125 enrollment fee, includes five free visits, and costs an additional $8 per visit after the first five. How many visits over a one-year period would a person who purchases the second package need to use for the cost to equal that of the one-year membership?

  1. 20
  2. 25
  3. 30
  4. 40

You need to know this:

The SAT likes to test your understanding of how to describe real-world situations using math equations. For some questions, it will be up to you to extract and solve an equation; for others, you’ll have to interpret an equation in a real-life context. The following table shows some of the most common phrases and mathematical equivalents you’re likely to see on the SAT.

Word Problems Translation Table
English Math
equals, is, equivalent to, was, will be, has, costs, adds up to, the same as, as much as =
times, of, multiplied by, product of, twice, double ×
divided by, out of, ratio ÷
plus, added to, sum, combined, increased by +
minus, subtracted from, smaller than, less than, fewer, decreased by, difference between –
a number, how much, how many, what x, n, etc.

Page 47

You need to do this:

When translating from English to math, start by defining the variables, choosing letters that make sense. Then, break down the question into small pieces, writing down the translation for one phrase at a time.

Explanation:

The phrase “how many visits” indicates an unknown, so you need a variable. Use an intuitive letter to represent the number of visits; call it v. The question asks when the two memberships will cost the “same amount,” so write an equation that sets the total membership costs equal to each other.

The first membership type costs $325 for unlimited visits, so write 325 on one side of the equal sign. The second type costs $8 per visit (not including, or except, the first 5 visits), or 8(v − 5), plus a flat $125 enrollment fee, so write 8(v − 5) + 125 on the other side of the equal sign. That’s it! Now solve for v:

The answer is (C).

Page 48

Try on Your Own

Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.

  1. A local restaurant is hosting a dance-a-thon for charity. Each couple must dance a minimum of three hours before earning any money for the charity. After the first three hours, couples earn $50 per half-hour of continuous dancing. Which expression represents the total amount earned by a couple who dance h hours, assuming they dance at least three hours?

    1. 25h
    2. 100h
    3. 50(h – 3)
    4. 100h – 300

  1. The final value, v, in a four-digit lock code is determined by multiplying the second value by two, subtracting that expression from the first value, and dividing the resulting expression by half of the third value. The first value is f, the second value is 1, and the third value is t. What is the final value, v, in terms of f andt?

  1. A pizzeria’s top-selling pizzas are The Works and The Hawaiian. The Works sells for $17, and The Hawaiian sells for $13. Ingredient costs for The Works are $450 per week, and ingredient costs for The Hawaiian are $310 per week. If x represents the number of each type of pizza sold in one week,  and the weekly profit from the sale of each type of pizza is the same, what is the value of x ?

    1. 30
    2. 35
    3. 140
    4. 145

  2. A student opens a checking account when she starts a new job so that her paychecks can be directly deposited into the account.  Her balance can be computed using the expression 10nw + 50, where n is the number of hours she works every week and w is the number of weeks that she has worked so far.  Assuming she does not withdraw any money from her account, which of the terms in the expression most logically will change if the student gets a raise?

    1. 10
    2. n
    3. w
    4. The expression will not change if the student gets a raise.

  3. Page 49Malik starts a job at which his starting salary is $25,500 per year. He expects that his salary will increase by a constant dollar amount annually. In 12 years, his salary will be double his starting salary. Assuming salary increases take place only at the end of a full year, how many years must Malik wait until his salary is at least $40,000 annually?

Page 50

Linear Graphs

To answer a question like this:

  1. What is the equation of the line that passes through the points (−3, −1) and (1, 3) ?

    1. y = −x + 2
    2. y = −x − 2
    3. y = x − 2
    4. y = x + 2

You need to know this:

The answer choices in this question are written in slope-intercept form: y = mx + b. In this form of a linear equation, m represents the slope of the line and b represents the y-intercept. You can think of the slope of a line as how steep it is. The y-intercept is the point at which the line crosses the y-axis and can be written as the ordered pair (0, y).

You can calculate the slope of a line if you know any two points on the line. The formula is , where (x1, y1) and (x2, y2) are the coordinates of the two points on the line.

A line that moves from the bottom left to the top right has a positive slope. A line that moves from the top left to the bottom right has a negative slope. A horizontal line has a slope of 0 and a vertical line has an undefined slope.

Some SAT questions ask about parallel or perpendicular lines. Parallel lines have the same slope, while perpendicular lines have negative reciprocal slopes.Page 51

You need to do this:

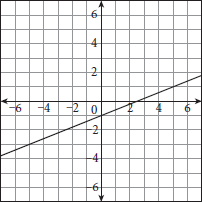
Explanation:

In this question, 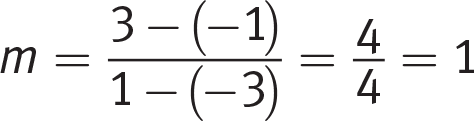. Of the answer choices, only (C) and (D) have a slope of 1, so rule out (A) and (B), which both have a slope of −1.

To find the y-intercept of the line, write the equation for the line in slope-intercept form and plug in one of the known points for x and y:

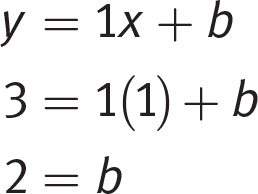
The correct answer is (D). For the record, here is the graph of the line. Note that as you would expect from the fact that m is positive, the line moves from the lower left to upper right, and it crosses the y-axis at the y-intercept of b = 2.

A line graphed on a coordinate plane. The line rises from left to right and passes through the points zero comma 2, and 2 comma 4

Page 52

Try on Your Own

Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.

  1. Line A passes through the coordinate points (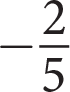, 0) and (0, 1). Which of the following lines will line A never intersect?

    1. A line graphed on a coordinate plane. The line rises from left to right, crosses the y-axis at zero comma negative one, and crosses the x-axis at 2.5 comma zero.
    2. A line graphed on a coordinate plane. The line rises from left to right, crosses the y-axis at zero comma one, and crosses the x-axis at negative one-half comma zero.
    3. A line graphed on a coordinate plane. The line falls from left to right, crosses the y-axis at zero comma one, and crosses the x-axis at 2.5 comma zero.
    4. A line graphed on a coordinate plane. The line falls from left to right, crosses the y-axis at zero comma one, and crosses the x-axis at one-half comma zero.

  2. In the xy-plane, the point (4, 7) lies on the line t, which is perpendicular to the line . What is the equation of line t ?

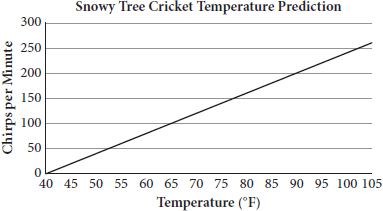
The graph is titled Snowy Tree Cricket Temperature Prediction. Chirps per minute are plotted along the vertical axis from zero to 300 in increments of 50. Temperature, in degrees Fahrenheit, is plotted along the horizontal axis from 40 to 105 in increments of 5. The line rises from left to right, and passes through the points 40 comma zero, and 65 comma 100.

  1. The graph shows the correlation between ambient air temperature, t, in degrees Fahrenheit and the number of chirps, c, per minute that a snowy tree cricket makes at that temperature. Which of the following equations represents the line shown in the graph?

Page 53

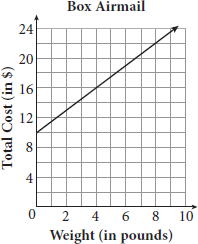
The graph is titled Box Airmail. Total cost, in dollars, is plotted along the vertical axis from zero to 24 in increments of 4. Weight, in pounds, is plotted along the horizontal axis from zero to 10 in increments of 2. The line begins at zero comma 10 and passes through the points 4 comma 16 and 8 comma 22.

  1. A freight airline charges a flat fee to airmail a box, plus an additional charge for each pound the box weighs. The graph above shows the relationship between the weight of the box and the total cost to airmail it. Based on the graph, how much would it cost in dollars to airmail a 40-pound box?

Minutes Charging 10 15 30
Percent Charged 347 41.5 64

  1. Xia is charging her laptop. She records the battery charge for the first 30 minutes after she plugs it in to get an idea of when it will be completely charged. The table above shows the results. If y is the percent battery charge on Xia’s laptop, which linear equation represents the correct relationship between y and x ?

    1. y = 1.5x + 19
    2. y = 2x + 14
    3. y = 2.5x + 9
    4. y = 10x + 34

Page 54

How Much Have You Learned?

Directions: For testlike practice, give yourself 15 minutes to complete this question set. Be sure to study the explanations, even for questions you got right. They can be found at the end of this chapter.

  1. Which value of x makes the equation 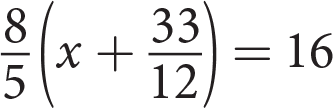true?

    1.   7.25
    2.   8.75
    3. 12.75
    4. 13.25
    Total cost in dollars is plotted along the vertical axis from 19 to 23 in increments of 1. Number of songs purchased is plotted along the horizontal axis from 0 to 8 in increments of 2. The line begins on the left at the point zero comma 20 and passes through the points 2 comma 20.5 and 6 comma 21.5.

  2. The graph above shows the cost of joining and buying music from a music subscription service. What does the y-intercept of the line most likely represent?

    1. The cost per song
    2. The cost to join the service
    3. The cost of buying 20 songs
    4. The cost of 20 subscriptions to the service

  3. If 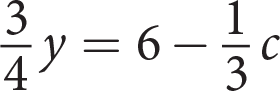 , then what is the value of   ?

  4. Three years ago, Madison High School started charging an admission fee for basketball games to raise money for new bleachers. The initial price was $2 per person; the school raised the price of admission to $2.50 this year. Assuming this trend continues, which of the following equations can be used to describe c, the cost of admission, y years after the school began charging for admission to games?

Page 56
Price of One Pound Projected Number of Pounds Sold
$1.20 15,000
$1.40 12,500
$1.60 10,000
$1.80 7,500
$2.00 5,000
$2.20 2,500

  1. Which of the following equations best describes the linear relationship shown in the table, where g represents the number of pounds of grain sold and d represents the price in dollars of one pound of grain?

    1. g = 1.2d + 12,500
    2. g = 12,500d + 15,000
    3. g = −12,500d + 17,500
    4. g = −12,500d + 30,000
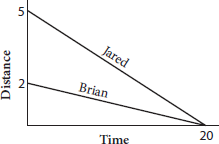
    The vertical axis is labeled Distance and the horizontal axis is labeled Time. The line labeled Jared starts at 5 on the Y-axis and ends at 20 on the X-axis. The line labeled Brian starts at 2 on the Y-axis and ends at 20 on the X-axis.

  2. Brian and Jared live in the same apartment complex and both bike to and from work every day. The figure above shows a typical commute home for each of them. Based on the figure, which of the following statements is true?

    1. It takes Brian longer to bike home because his work is farther away.
    2. It takes Jared longer to bike home because his work is farther away.
    3. Jared and Brian arrive home at the same time, so they must bike at about the same rate.
    4. Jared bikes a longer distance than Brian in the same amount of time, so Jared must bike at a faster rate.

  3. When graphing a linear equation that is written in the form y = mx + b, the variable m represents the slope of the line and b represents the y-intercept. Assuming that b > 0, which of the following best describes how reversing the sign of b will affect the graph?

    1. The new line will be shifted down b units.
    2. The new line will be shifted down 2b units.
    3. The new line will be a perfect reflection across the x-axis.
    4. The new line will be a perfect reflection across the y-axis.

  4. The graph of a line in the xy-plane passes through the points (5, 4) and . Which of the following equations describes the line?

    Page 57

  5. Line f in the xy-plane passes through the origin and has a slope of . Line z is perpendicular to line f and passes through the point (6, 2). Which of the following is the equation of line z ?

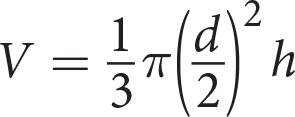
  6. A circle of rubber with a constant diameter d is placed on a table; its perimeter is anchored to the table and a string is attached to its center. When the string is pulled upwards, a cone is formed with height h and volume V. The relationship between d, h, and V is represented above. Which of the following statements must be true?

    1. As the volume of the cone decreases, the height also decreases.
    2. If the diameter of the base of the cone is 6 centimeters, the height can be determined by dividing the volume by .
    3. If the height of the cone triples, the volume must also triple.
    1. I only
    2. I and II only
    3. II and III only
    4. I, II, and III

Page 58

Reflect

Directions: Take a few minutes to recall what you’ve learned and what you’ve been practicing in this chapter. Consider the following questions, jot down your best answer for each one, and then compare your reflections to the expert responses on the following page. Use your level of confidence to to determine what to do next.

What should you do to isolate a particular variable in an equation?

What types of key words should you look for when translating English into math?

What is the most useful equation for a line in the coordinate plane? Why?

When the SAT gives you two points on a line, what can you figure out?

How are parallel and perpendicular lines related to each other?

Page 59

Expert Responses

What should you do to isolate a particular variable in an equation?

Perform inverse operations until the variable is by itself on one side of the equal sign. If the equation has fractions, make them disappear by multiplying both sides of the equation by the denominator(s). If like terms appear on different sides of the equation, collect them on the same side so that you can combine them.

What types of key words should you look for when translating English into math?

Look for key words that signal equality (“is,” “has,” “was”), variable names (“Marina’s age,” “the cost of one bathtub”), or one of the four arithmetic operations (addition, subtraction, multiplication, and division).

What is the most useful equation for a line in the coordinate plane? Why?

The best equation is slope-intercept form, y = mx + b, because it tells you the slope (m) and the y-intercept (b). Conversely, if you need to derive an equation yourself, you can plug the slope and y-intercept into slope-intercept form and you’re done.

When the SAT gives you two points on a line, what can you figure out?

If you know two points, you can figure out the slope of the line with the equation 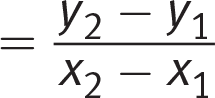. From there, you can plug one of the points and the slope into slope-intercept form and find the y‑intercept.

How are parallel and perpendicular lines related to each other?

Parallel lines never intersect and they have equal slopes. Perpendicular lines intersect at a 90° angle and they have negative reciprocal slopes.

Next Steps

If you answered most questions correctly in the “How Much Have You Learned?” section, and if your responses to the Reflect questions were similar to those of the SAT expert, then consider linear equations and graphs an area of strength and move on to the next chapter. Come back to this topic periodically to prevent yourself from getting rusty.

If you don’t yet feel confident, review those parts of this chapter that you have not yet mastered. In particular, review the variable isolation drills in the Solving Equations lesson and the definition of slope-intercept form in the Linear Graphs lesson. Then try the questions you missed again. As always, be sure to review the explanations closely.Page 60

Answers and Explanations

Solving Equations

  1. D

    Difficulty: Easy

    Getting to the Answer: Distribute the factor of 2, combine like terms, multiply both sides of the equation by 2 to clear the fraction, and then solve for y:

    Choice (D) is correct.

  2. C

    Difficulty: Hard

    Strategic Advice: Complicated-looking equations appear difficult, but they always succumb to the steps of solving an equation. First, clear the equation of fractions, then collect like terms, and solve for the desired variable.

    Getting to the Answer: Clear the equation of the fraction in the numerator by multiplying both sides by 4 to yield: 

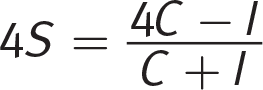
    Now, multiply both sides by the denominator C + I to clear the equation of fractions:

    Distribute the 4S:

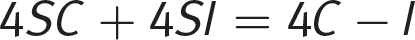
    To solve for I, collect all the terms that include I on one side of the equation:

     Factor out the I:

    Divide to isolate I, and factor out 4C from the numerator:

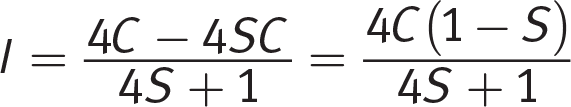
    (C) is correct.

  3. 18

    Difficulty: Easy

    Getting to the Answer: First, clear the fractions by multiplying both sides of the equation by 8. Then solve for x using inverse operations:

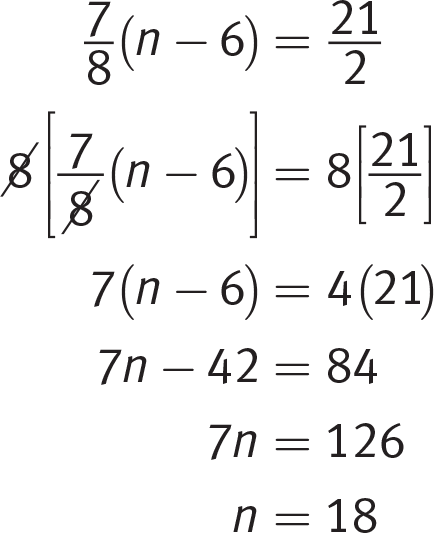
    Grid in 18.

  4. A

    Difficulty: Medium

    Strategic Advice: Noticing key information about the answer choices and using that information to pick numbers saves time by eliminating algebra.

    Getting to the Answer: Rearranging the terms of the equation such that  is on one side and the constants are all on the other will work for this problem. First, cross-multiply to get rid of the fractions. Then, use inverse operations to isolate :

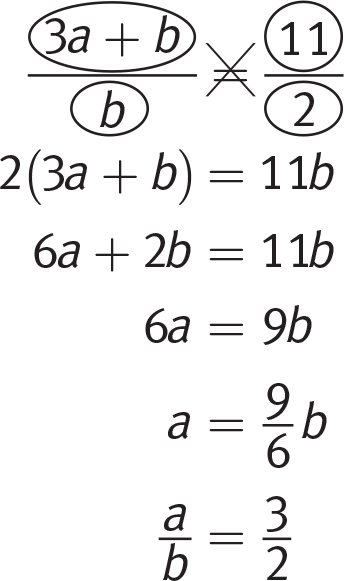
    The answer is (A).

    Page 61There is a faster approach. Notice that 2 shows up in the denominator in most of the choices, indicating that it is likely that b equals 2. If b = 2 , then a must be 3 for the numerator to equal 11. Test this by plugging the numbers into the equation: 

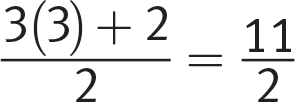
    Thus, , confirming (A) as the answer. You can avoid a lot of work by using key information in the answer choices to pick numbers.

  5. D

    Difficulty: Medium

    Getting to the Answer: Simplify the numerators as much as possible, then isolate the variable. Begin by combining like terms on both sides of the equation. Then cross-multiply and solve for z:

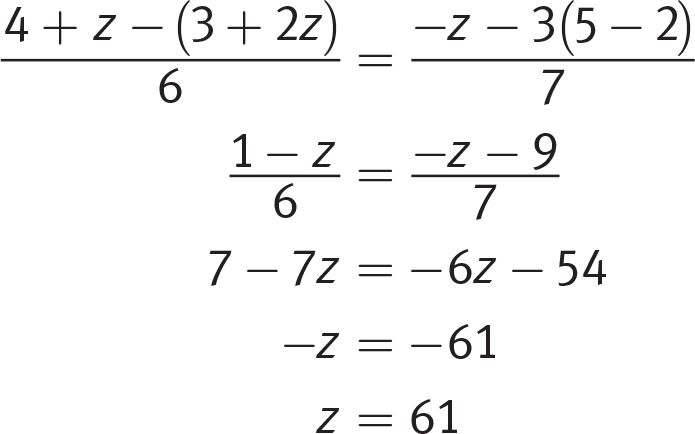
    Choice (D) is correct.

Word Problems

  1. D

    Difficulty: Medium

    Getting to the Answer: Use the information in the question to write your own expression, then look for the answer choice that matches. Simplify your expression only if you don’t find a match. If a couple earns $50 per half-hour that they dance, then they earn 50 × 2 = $100 per hour. Multiply this amount by the number of hours (not including the first 3 hours). This can be expressed as 100(h − 3). This is not one of the answer choices, so simplify by distributing the 100 to get 100h − 300, which is (D).

    If you’re struggling with the algebra, try Picking Numbers. Pick a number of hours a couple might dance, like 5. They don’t earn anything for the first 3 hours, but they earn $50 per half-hour for the last 2 hours, which is 50 times 4 half-hours, or $200. Now, find the expression that gives you an answer of $200 when h = 5 hours: 100(5) − 300 = 500 − 300 = 200. If you use Picking Numbers, remember that it is possible that the number you choose satisfies more than one answer choice, so plug it in to the other three choices. In this case, h = 5 does not give a value of 200 in any other equation, which confirms that (D) is correct.

  2. B

    Difficulty: Medium

    Getting to the Answer: Translate piece by piece to get a final expression for the final value, v. Multiply the second value by 2 to get 2(1) = 2. Subtract that from the first value to get f − 2. Divide this expression by half of the third value to get 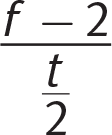, which you can simplify by multiplying by the reciprocal: 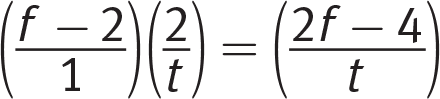. Choice (B) matches the final expression. Watch out for (D), the trap answer choice that switches the variables.

  3. B

    Difficulty: Medium

    Getting to the Answer: Write expressions to represent the profit generated by selling each type of pizza. You’re told The Works sells for $17 each and that its ingredients cost the pizzeria $450 per week. This means the weekly profit generated by this pizza’s sales can be represented by the expression  17x − 450. Do the same for The Hawaiian: Each one sells for $13, but the pizzeria loses $310 to pay for ingredients each week. Therefore, the weekly profit from this pizza can be represented by  13x − 310. To determine the value of x at which the profit from the sale of each type of pizza is the same, set the two profit expressions equal to each other and solve:

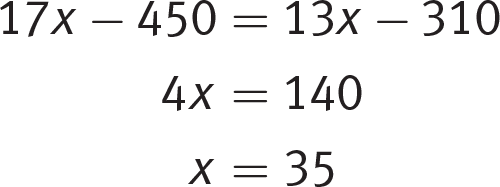
    Thus, (B) is correct. Always be sure you’re answering the right question; choice (D), 145, is the profit when x = 35.

    Page 62

  4. A

    Difficulty: Easy

    Getting to the Answer: When faced with a question that includes abstract expressions, it is helpful to pick concrete numbers to work with. These numbers don’t have to be realistic; just choose numbers that are easy to work with. Suppose the student checks her balance after 2 weeks working 3 hours each week. She would have worked a total of 6 hours, which would have to be multiplied by the amount she is paid per hour to get her total pay.  In the expression, plugging in w = 3 and n = 2 demonstrates that the number 10 in the expression must be the amount that she is paid per hour, and thus is the term that would change if the student got a raise. (A) is correct. Although 50 is not an answer choice, you can deduce that it must have been her checking account’s original balance because it is a constant.

  5. 7

    Difficulty: Medium

    Getting to the Answer: First, notice that the actual dollar amount of the increase each year is unknown, so assign a variable like d. After 12 increases, his salary will rise by $25,500, so write a formula . Solve for d to find that Malik will receive an increase of $2,125 per year.

    The question asks how many years must go by until Malik’s salary is at least $40,000; the number of years is another unknown, so assign it a variable like n. Multiplying n by the amount of each increase will give you the total increase of dollars over n years, but don’t forget to add in the starting salary to reflect his total salary amount:

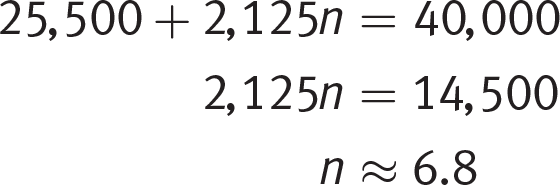
    The question asks you to assume that salary increases only take place at the end of a full year. If you are unsure and want to prove that the answer is not 6, check by using n = 6 to calculate the total dollar amount: 25,500 + 2,125(6)= 38,250. Six years is not long enough; grid in 7.

Linear Graphs

  1. B

    Difficulty: Easy

    Getting to the Answer: You’re asked to identify the line that the one described in the question stem will never intersect. Lines that never intersect are parallel and therefore have identical slopes, so start by finding the slope of the line whose two coordinate pairs are given. You’ll find:

    Choices (C) and (D) have negative slopes, so eliminate them. Next, find the slopes of (A) and (B). No need to use the slope formula; counting units on the graphs will be faster. The slope of (A) is  because for every 2 units the line rises, it runs 5 units to the right. The slope of (B) is  because when the line goes up 5 units, it goes 2 units to the right. Therefore, (B) is correct.

  2. A

    Difficulty: Medium

    Strategic Advice: Remember that parallel lines have the same slope and perpendicular lines have opposite sign reciprocal slopes.

    Getting to the Answer: The first useful piece of information is that the slope of the line perpendicular to line t is 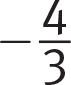. Perpendicular lines have negative reciprocal slopes, so the slope of line t is . Eliminate (B) and (D) because they have the incorrect slopes.

    Plug the values for the slope and the coordinate point (4, 7) into the slope-intercept equation to solve for b:

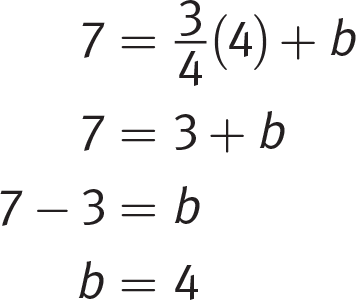
    Eliminate (C) because it does not have the correct y-intercept. Choice (A) is correct.

    Page 63

  3. A

    Difficulty: Medium

    Getting to the Answer: Start by finding the slope of the line by picking a pair of points, such as (40, 0) and (65, 100): 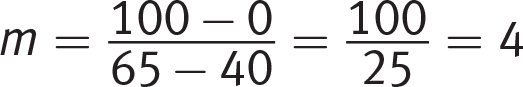 . Choices (B) and (C) have slopes other than 4, so eliminate them. Choices (A) and (D) have y-intercepts of −160 and 40, respectively. Now, read the axis labels carefully: the horizontal axis begins at 40 (not 0). The line is trending downward as x-values get smaller, so the y-intercept (when x = 0) must be well below 0 on the vertical axis. Therefore, the answer must be (A).

  4. 70

    Difficulty: Hard

    Getting to the Answer: Because 40 pounds is not shown on the graph, you need more information. In a real-world scenario, the y-intercept of a graph usually represents a flat fee or a starting amount. The slope of the line represents a unit rate, such as the cost per pound to airmail the box. 

    The y-intercept of the graph is 10, so the flat fee is $10. To find the cost per pound (the unit rate), substitute two points from the graph into the slope formula. Using the points (0, 10) and (4, 16), the cost per pound is , which means it costs $1.50 per pound to airmail a box. The total cost to airmail a 40-pound box is $10 + 1.50(40) = $10 + $60 = $70. Grid in 70.

  5. A

    Difficulty: Hard

    Getting to the Answer: The question tells you that the relationship is linear, so start by finding the rate of change (the slope, m) using any two pairs of values from the table and the slope formula. Next, substitute the slope and any pair of values from the table, such as (10, 34), into the equation y = mx + b and solve for b. Finally, use the values of m and b to write the function.

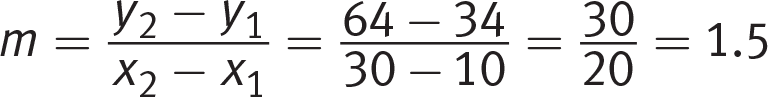
    You can stop right there! Only (A) has a slope of 1.5, so it must be the correct answer. For the record:

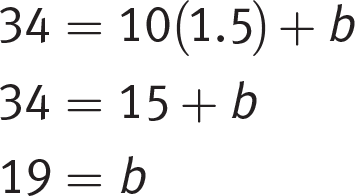
On Test Day

  1. B

    Difficulty: Hard

    Strategic Advice: Watch out for the “NOT” keyword in the question stem. Picking numbers based on clues in the equation is faster than doing the algebra.  

    Getting to the Answer: To find the answer using Picking Numbers, take advantage of the fact that the equation is a proportion (that is, two fractions equal to each other). If b = 7 and 2(a − 3) = 4, then both fractions will be the same and the numbers you’ve picked will be valid. Solve for a: a − 3 = 2, and a = 5. Now plug b = 7 and a = 5 into the choices, looking for the one that ISN’T true:

    (A) 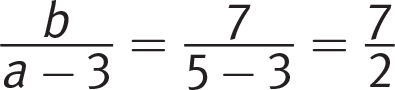, eliminate.

    (B)  

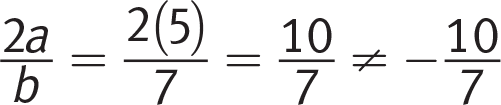
    You’re done; pick (B) and move on. For the record:

    (C) , eliminate.

    (D) 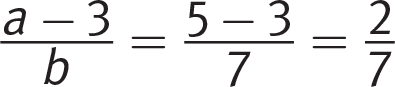 , eliminate.

    To solve this question using algebra, first cross-multiply and simplify the original equation:

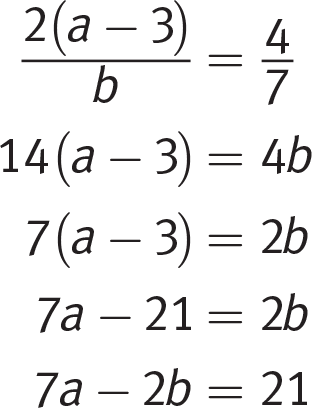
    Then, repeat this entire process for each answer choice, looking for the one that doesn’t yield the same equation:
    (A) , eliminate.
    (B)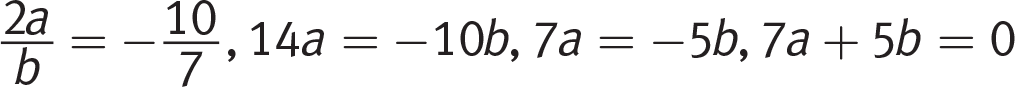 

    This equation is different from the one in the question, so (B) is correct. For the record:
    (C) , eliminate.
    (D)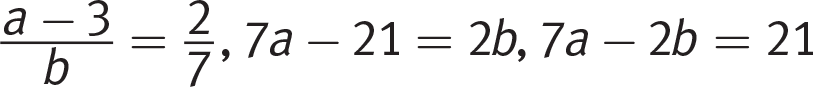 , eliminate.

How Much Have You Learned?

Page 64

  1. A

    Difficulty: Medium

    Category: Solving Equations

    Getting to the Answer: This question has multiple fractions, so clear the 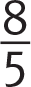by multiplying both sides of the equation by its reciprocal, . Then, because the answers are given in decimal form, change the other fraction to a decimal by dividing the numerator by the denominator.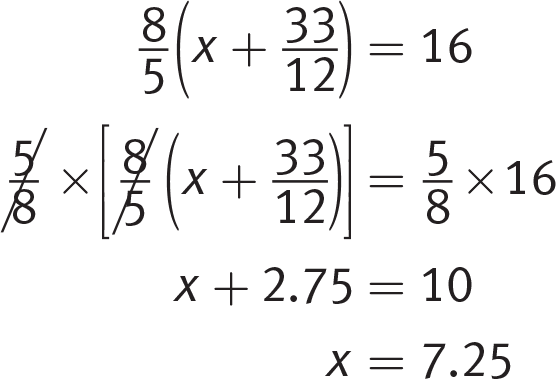

    (A) is correct.

  2. B

    Difficulty: Easy

    Category: Linear Graphs

    Getting to the Answer: Read the axis labels carefully. The y-intercept is the point at which x = 0, which means the number of songs purchased is 0. The y-intercept is (0, 20), so the cost is $20 before buying any songs and therefore most likely represents a flat membership fee for joining the service. (B) is correct.

  3. 36

    Difficulty: Medium

    Category: Solving Equations

    Getting to the Answer: When you’re asked to find an expression rather than a variable value, it means there’s likely a shortcut: try to make the expression you have look like the expression you want. Start by eliminating the fractions. A common multiple of 4 and 3 is 12, so multiply both sides of the equation by that. Once the fractions are gone, move both variable terms to the same side:

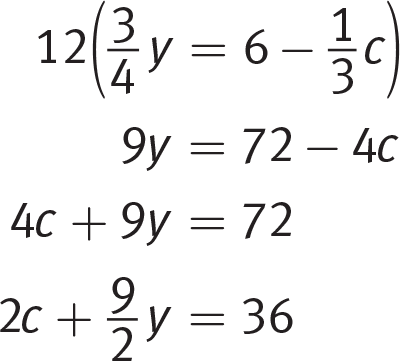
    The expression on the left side is precisely what you’re looking for, so grid in 36.

  4. C

    Difficulty: Medium

    Category: Word Problems

    Getting to the Answer: Look closely; buried in the text are two sets of coordinates you can use. The question states that admission was $2 when the admission charge was first implemented and increased to $2.50 after 3 years, making your coordinates (0, 2) and (3, 2.5). The slope of the line passing through these is 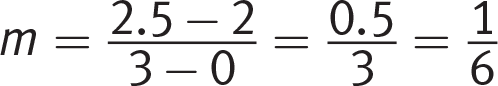. Eliminate (A) and (D). Because the admission fee started at $2, 2 is the y-intercept, so the full equation is . (C) is correct.

    Because the question says “three years ago,” it may be tempting to use (–3, 2) and (0, 2.5) as your coordinates. Think about what that would mean: the first admission charge would be $2.50, as it’s impossible to have a negative year. This contradicts the question stem, so (B) is incorrect.

  5. D

    Difficulty: Medium

    Category: Word Problems

    Getting to the Answer: Take a quick peek at the answer choices. The equations are given in slope-intercept form, so start by finding the slope. Substitute two pairs of values from the table (try to pick easy ones, if possible) into the slope formula, 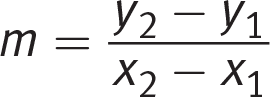. Keep in mind that the projected number of pounds sold depends on the price, so the price is the independent variable (x) and the projected number is the dependent variable (y). Using the points (1.2, 15,000) and (2.2, 2,500), you can find the slope:

    This means you can eliminate (A) and (B) because the slope is not correct. Don’t let (B) fool you—the projected number of pounds sold goes down as the price goes up, so there is an inverse relationship, which means the slope must be negative. To choose between (C) and (D), you could find the y-intercept of the line. Pick a point with easy values, such as (2, 5,000), and plug in 5,000 for y and 2 for x:Page 65

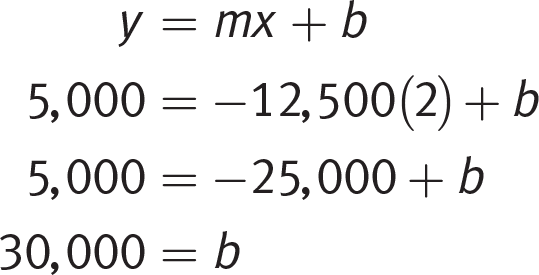
    (D) is correct. Another option is to substitute (2, 5,000) into (C) and (D) only. Again, (D) is correct because 5,000 = −12,500(2) + 30,000 is a true statement.

  6. D

    Difficulty: Medium

    Category: Word Problems

    Getting to the Answer: Consider each choice systematically, using the numbers on the figure to help you evaluate each statement.

    It takes Brian and Jared each 20 minutes to bike home, so (A) and (B) are false. Jared bikes 5 miles in 20 minutes, while Brian only bikes 2 miles in 20 minutes; their rates are not the same, so (C) is false. This means (D) must be true. Jared starts out farther away than Brian, so Jared must bike at a faster rate to arrive home in the same amount of time.

  7. B

    Difficulty: Hard

    Category: Linear Graphs

    Getting to the Answer: You aren’t given any numbers in this question, so make some up. Sketch a quick graph of any simple linear equation that has a positive y-intercept (because it is given that b > 0). Then, change the sign of the y-intercept and sketch the new graph on the same coordinate plane. Pick a simple equation that you can sketch quickly, such as y = x + 3, and then change the sign of b. The new equation is y = x − 3. Sketch both graphs. The second line is shifted down 6 units, and because b = 3, 6 is 2b units. (B) is correct. The graph that follows illustrates this. If you’re still unsure, try another pair of equations.

    The solid line is labeled Y equals X plus 3. The dashed line is labeled Y equals X minus 3. The dashed line is six units below the solid line.

  8. C

    Difficulty: Medium

    Category: Linear Graphs

    Strategic Advice: Be careful when the answer choices look very similar to each other. Eliminating incorrect answers during intermediate steps lowers your odds of making a careless mistake.

    Getting to the Answer: The question provides two coordinate points, which means that the best approach is to find the slope using the formula m = 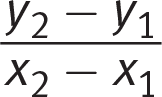 , then use the slope-intercept equation for a line to find b, the y-intercept . Plugging the results into the slope formula results in:

    Eliminate (B) and (D) because they do not have the slope 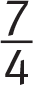. Plug the slope and one of the given points (5, 4) into the slope-intercept equation to solve for b: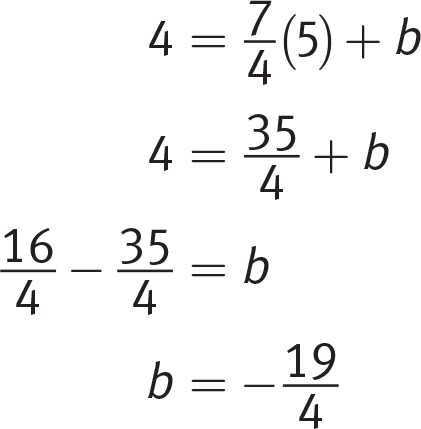

    Eliminate (A) because it does not have the correct y-intercept; therefore only (C) is left and is correct. Plugging the calculated values for the slope and the y-intercept into the slope-intercept equation indeed gives you choice (C): .

    After eliminating (B) and (D), you can save time by noticing that the two possible y-intercepts are 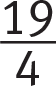 and 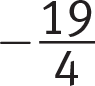. You really only need to determine if b is positive or negative.Page 66

  9. D

    Difficulty: Easy

    Category: Linear Graphs

    Getting to the Answer: This question provides an equation for a line perpendicular to line z and a coordinate point for line z, (6, 2). The opposite sign reciprocal of the slope of the perpendicular line, , is the slope of line z. Eliminate (A) and (B) because they have the incorrect slope.

    Plug the values for the slope and the coordinate point (6, 2) into the slope-intercept equation to solve for b:

    Plug the values for the slope and the y-intercept into the slope-intercept equation to get 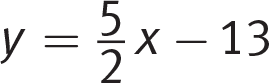. (D) is correct.

    You can save a little time if you eliminate (C) as soon as you see that b ≠ 0, which you should be able to tell as soon as you see that 2 = 15 + b.

  10. D

    Difficulty: Hard

    Category: Word Problems

    Strategic Advice: In problems that include verifying statements marked with roman numerals, start with the easiest statement to verify and work to the hardest, eliminating answer choices along the way. This may save you time on test day.

    Getting to the Answer: The key to this problem is to see that because the question stem states that d is constant, the cumbersome expression 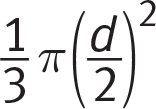 is just a constant that is the coefficient of the variable h.  The formula is really V = (some constant) × h. In any formula written such that y = ax, where a is a constant, as one amount increases (or decreases), the other amount must increase (or decrease) at the same rate. So if V decreases, h must have decreased. Statement I is true; eliminate (C). 

    Pick the next easiest statement to verify; in this case, statement III.  If h increases by tripling, V must also increase by the same rate; it must triple, too. Test this statement if you like by picking a number for h and solving for V, then tripling h and solving for V again.  Statement III is true; eliminate (A) and (B). That leaves (D) as the correct answer.

    On test day, you’d stop here. For the sake of learning, though, you can verify whether statement II is true. Plug d = 6 into the formula and solve for h in terms of V: 

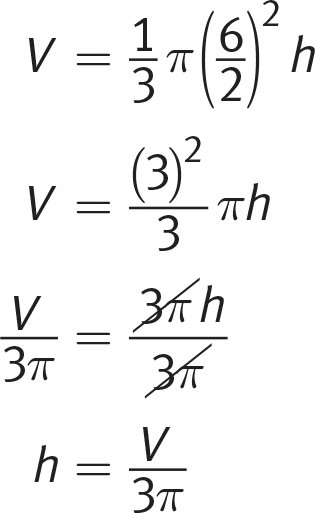
    Thus, statement II is indeed true.