Chapter 5
Systems of Linear Equations
Page 68
How Much Do You Know?
Directions: Try the questions that follow. Show your work so that you can compare your solutions to the ones found in the Check Your Work section immediately after this question set. The “Category” heading in the explanation for each question gives the title of the lesson that covers how to solve it. If you answered the question(s) for a given lesson correctly, and if your scratchwork looks like ours, you may be able to move quickly through that lesson. If you answered incorrectly or used a different approach, you may want to take your time on that lesson.

-
In the system of equations above, what is the value of x ?
- −2
- 0
- 2
- 4
-
At a certain movie theater, there are 16 rows and each row has either 20 or 24 seats. If the total number of seats in all 16 rows is 348, how many rows have 24 seats?
- 7
- 9
- 11
- 13
-
If 17x − 5y = 8 and 14x − 7y = −7, what is the value of 3x + 2y ?
- −15
- −5
- 5
- 15
-
If 0.2x = 10 − 0.5y, then 10y + 4x =
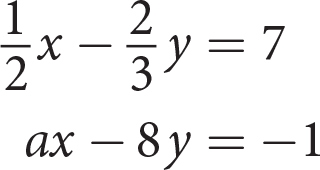
-
If the system of linear equations above has no solution, and a is a constant, then what is the value of a?
- −2

- 2
- 6
Page 70
Check Your Work
-
A
Difficulty: Easy
Category: Substitution
Getting to the Answer: Solve the second equation for y in terms of x, then substitute into the first equation and solve:
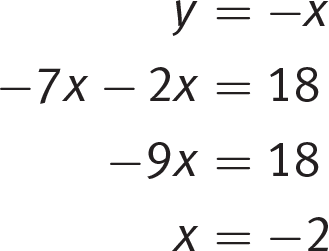
(A) is correct.
-
A
Difficulty: Hard
Category: Substitution
Getting to the Answer: Create a system of equations in which x represents the number of rows with 20 seats and y represents the number of rows with 24 seats. The first equation should represent the total number of rows, each with 20 or 24 seats, or x + y = 16. The second equation should represent the total number of seats. Because x represents rows with 20 seats and y represents rows with 24 seats, the second equation should be 20x + 24y = 348. Now solve the system using substitution. Solve the first equation for either variable and substitute the result into the second equation:

So 7 rows have 24 seats, which means (A) is correct. This is all the question asks for, so you don’t need to find the value of x.
-
D
Difficulty: Medium
Category: Combination
Getting to the Answer: Subtract the second equation from the first to find that 3x + 2y = 15, making (D) the correct answer.
-
200
Difficulty: Medium
Category: Number of Possible Solutions
Getting to the Answer: Rearrange the equation so that the y and x terms appear, in that order, on the left side: 0.5y + 0.2x = 10. What number do you need to multiply 0.5y by to get 10y? Twenty. Notice that 10y + 4x is 20 times 0.5y + 0.2x. Multiply both sides of the equation by 20 to find that 10y + 4x = 200. Note that both of these equations describe the same line.
-
D
Difficulty: Hard
Category: Number of Possible Solutions
Getting to the Answer: Graphically, a system of linear equations that has no solution indicates two parallel lines—that is, two lines that have the same slope but different y-intercepts. To have the same slope, the x- and y-coefficients must be the same. To get from
 to −8, you multiply by 12, so multiply
to −8, you multiply by 12, so multiply  by 12 as well to yield 6x. Because the other x-coefficient is a, it must be that a = 6, and (D) is correct. Note that, even though it is more work, you could also write each equation in slope-intercept form and set the slopes equal to each other to solve for a.
by 12 as well to yield 6x. Because the other x-coefficient is a, it must be that a = 6, and (D) is correct. Note that, even though it is more work, you could also write each equation in slope-intercept form and set the slopes equal to each other to solve for a.
Substitution
To answer a question like this:
-
If 3x + 2y = 15 and x + y = 10, what is the value of y ?
- −15
- −5
- 5
- 15
You need to know this:
A system of two linear equations simply refers to the equations of two lines. “Solving” a system of two linear equations usually means finding the point where the two lines intersect. (However, see the lesson titled “Number of Possible Solutions” later in this chapter for exceptions.)
There are two ways to solve a system of linear equations: substitution and combination. For some SAT questions, substitution is faster; for others, combination is faster. We’ll cover combination in the next lesson.
You need to do this:
To solve a system of two linear equations by substitution:
- Isolate a variable (ideally, one whose coefficient is 1) in one of the equations
- Substitute the result into the other equation
Explanation:
Isolate x in the second equation, then substitute the result into the first equation:
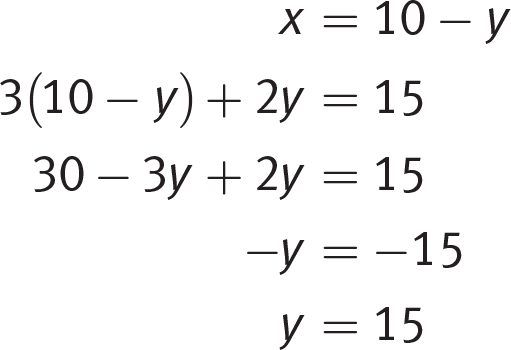
If you needed to know the value of x as well, you could now substitute 15 for y into either equation to find that x = −5. The correct answer is (D).Page 72
Try on Your Own
Directions: Solve these questions by substitution. Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.
-
If 7c + 8b = 15 and 3b − c = 2, what is the value of b ?


-
Given the system of equations above, what is the sum of x and y ?
- −10
- −5
- 0
- 5

-
If (x, y) is a solution to the system of equations above, then what is the value of x – y ?
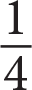
- 1
- 3
- 18
-
If 5a = 6b + 7 and a − b = 3, what is the value of
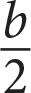 ?
?- 2
- 4
- 5.5
- 11
-
Marisol is selling snacks at her school’s soccer games to raise money for a service project. She buys nuts in cases that contain 24 bags and granola bars in cases that contain 20 packages. She sells the nuts for $1.25 a bag and the granola bars for $1.75 a package. If she raised $160 and sold 112 items, how many cases of granola bars did Marisol buy?
- 2
- 3
- 40
- 72
Page 73
Combination
To answer a question like this:
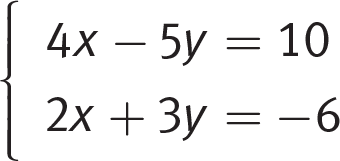
If the solution to the system of equations above is (x, y), what is the value of y ?
- –2
- –1
- 1
- 2
You need to know this:
Combining two equations means adding or subtracting them, usually with the goal of either eliminating one of the variables or solving for a combination of variables (e.g., 5n + 5m).
You need to do this:
To solve a system of two linear equations by combination:
- Make sure that the coefficients for one variable have the same absolute value. (If they don’t, multiply one equation by an appropriate constant. Sometimes, you’ll have to multiply both equations by constants.)
- Either add or subtract the equations to eliminate one variable
- Solve for the remaining variable, then substitute its value into either equation to solve for the variable you eliminated in the preceding step
Page 74
Explanation:
Both variables have different coefficients in the two equations, but you can convert the 2x in the second equation to 4x by multiplying the entire second equation by 2:

Now that the coefficients for one variable are the same, subtract the second equation from the first to eliminate the x variable. (Note that if the x-coefficients were 4 and −4, you would add the equations instead of subtracting.)
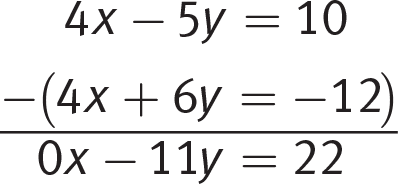
Solve this equation for y:
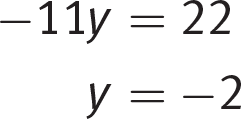
(A) is the correct answer. If the question asked for x instead of y, you would now substitute −2 into either of the original equations and solve for x. (For the record, x = 0.)Page 75
Try on Your Own
Directions: Solve these questions using combination. Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.
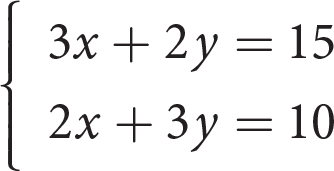
-
Given the system of equations above, what is the value of 5x + 5y ?

-
If 2x − 3y = 14 and 5x + 3y = 21, what is the value of x ?
- −1
- 0
-

- 5
-
If 7c − 2b = 15 and 3b − 6c = 2, what is the value of b + c ?
- −27
- −3
- 8
- 17
-
If y = −x − 15 and
 , then what is the value of 2x + 6y ?
, then what is the value of 2x + 6y ?
-
If 2x + 2y = 22 and 3x – 4y = 12, what is the value of
 ?
?

Number of Possible Solutions
To answer a question like this:
-
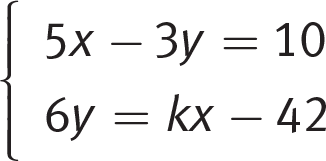
In the system of linear equations above, k represents a constant. If the system of equations has no solution, what is the value of 2k ?
-

- 5
- 10
- 20
-
You need to know this:
The solution to a system of linear equations consists of the values of the variables that make both equations true.
A system of linear equations may have one solution, infinitely many solutions, or no solution.
If a system of equations represents two lines that intersect, then the system will have exactly one solution (in which the x- and y-values correspond to the point of intersection).
If a system of equations has infinitely many solutions, the two equations actually represent the same line. For example, 2x + y = 15 and 4x + 2y = 30 represent the same line. If you divide the second equation by 2, you arrive at the first equation. Every point along this line is a solution.
If a system of equations has no solution, as in the question above, the lines are parallel: there is no point of intersection.

Page 77
You need to do this:
- If the question states that the system has no solution, manipulate the equations to make the x-coefficients equal to each other and the y-coefficients equal to each other, but be sure that the y-intercepts (or constant terms, if the equations are in ax + by + c form) are different.
- If the question states that the system has infinitely many solutions, make the x-coefficients equal to each other, the y-coefficients equal to each other, and the y-intercepts (or constant terms) equal to each other.
- If the question states that the system has one solution and provides the point of intersection, substitute the values at that point of intersection for x and y in the equations.
Explanation:
Start by recognizing that for two lines to be parallel, the coefficients for x must be identical in the two equations; ditto for the coefficients for y. Manipulate the second equation so that it is in the same format as the first one:

The y-coefficient in the first equation, 5x − 3y = 10, is 3. Divide the second equation by 2 in order to make the y-coefficients in both equations equal:

Now set the x-coefficient equal to the x-coefficient in the first equation:
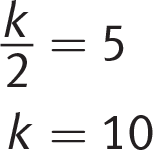
Note that the question asks for the value of 2k, so the correct answer is (D), 20.Page 78
Try on Your Own
Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.

-
The system of equations shown above has how many solutions?
- Zero
- One
- Two
- Infinitely many

-
In the system of linear equations above, q is a constant. If the system has infinitely many solutions, what is the value of q ?
- –9
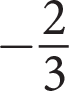
-

- 9

-
If the graphs of the lines in the system of equations above intersect at (–3, 1), what is the value of
 ?
?
- 2
- 3
- 6
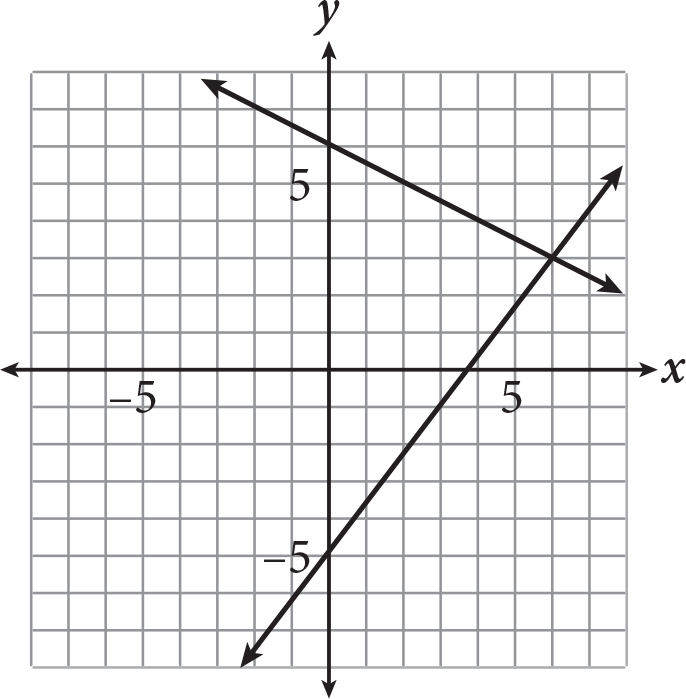
-
What is the y-coordinate of the solution to the system shown above?
- –5
- 3
- 5
- 6

-
If the system of linear equations above has infinitely many solutions, and c is a constant, what is the value of c ?
- −6
- −3
- −2
- −1
Page 79
How Much Have You Learned?
Directions: For testlike practice, give yourself 15 minutes to complete this question set. Be sure to study the explanations, even for questions you got right. They can be found at the end of this chapter.
-
If 8x − 2y = 10 and 3y − 9x = 12, then what is the value of y − x ?
- −8
- 2
- 12
- 22
-
A state college has separate fee rates for resident students and nonresident students. Resident students are charged $421 per semester and nonresident students are charged $879 per semester. The college’s sophomore class of 1,980 students paid a total of $1,170,210 in fees for the most recent semester. Which of the following systems of equations represents the number of resident (r) and nonresident (n) sophomores and the amount of fees the two groups paid?
- r + n = 1,170,210 421r + 879n = 1,980
- r + n = 1,980 879r + 421n = 1,170,210
- r + n = 1,980 421r + 879n = 1,170,210
- r + n = 1,170,210 879r + 421n = 1,980
-
A sofa costs $50 less than three times the cost of a chair. If the sofa and chair together cost $650, how much more does the sofa cost than the chair?
- $175
- $225
- $300
- $475
Equation 1 x y −2 6 0 4 2 2 4 0 Equation 2 x y −8 −8 −4 −7 0 −6 4 −5 -
The tables above represent data points for two linear equations. If the two equations form a system, what is the x-coordinate of the solution to that system?Page 81


-
If (A, B) is the solution to the system of equations shown above, and A and B are integers, then what is the value of A + B ?
- −12
- −6
- 0
- 6

-
If the system of linear equations above has infinitely many solutions, and k is a constant, what is the value of k ?
- −8
- −4
- −2
- −1
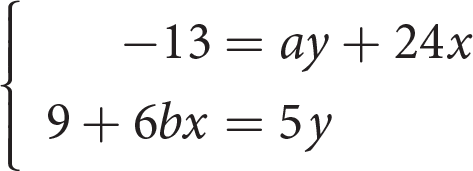
-
If the system of equations above has no solution, and a and b are constants, then what is the value of |a + b| ?
- 0
- 1
- 4
- 9
-
If
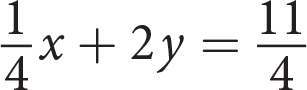 and −6y − x = 7, what is half of y ?
and −6y − x = 7, what is half of y ?
-
At a certain toy store, tiny stuffed pandas cost $3.50 and giant stuffed pandas cost $14. If the store sold 29 panda toys and made $217 in revenue in one week, how many tiny stuffed pandas and giant stuffed pandas were sold?
- 18 tiny stuffed pandas, 11 giant stuffed pandas
- 11 tiny stuffed pandas, 18 giant stuffed pandas
- 12 tiny stuffed pandas, 17 giant stuffed pandas
- 18 tiny stuffed pandas, 13 giant stuffed pandas
-
A bead shop sells wooden beads for $0.20 each and crystal beads for $0.50 each. If a jewelry artist buys 127 beads total and pays $41 for them, how much more did she spend on crystal beads than wooden beads?
- $11
- $15
- $23
- $26
Page 82
Reflect
Directions: Take a few minutes to recall what you’ve learned and what you’ve been practicing in this chapter. Consider the following questions, jot down your best answer for each one, and then compare your reflections to the expert responses on the following page. Use your level of confidence to determine what to do next.
When is substitution a good choice for solving a system of equations?
When is combination a good choice for solving a system of equations?
What does it mean if a system of equations has no solution? Infinitely many solutions?
Page 83
Expert Responses
When is substitution a good choice for solving a system of equations?
Substitution works best when at least one of the variables has a coefficient of 1, making the variable easy to isolate. This system, for example, is well suited for substitution:
a + 3b = 5
4a − 6b = 21
That’s because in the first equation, you can easily isolate a as a = 5 − 3b and plug that in for a in the other equation. By contrast, substitution would not be a great choice for solving this system:
2a + 3b = 5
4a − 6b = 21
If you used substitution now, you’d have to work with fractions, which is messy.
When is combination a good choice for solving a system of equations?
Combination is always a good choice. It is at its worst in systems such as this one:
2a + 3b = 5
3a + 5b = 7
Neither a coefficient is a multiple of the other, and neither b coefficient is a multiple of the other, so to solve this system with combination you’d have to multiply both equations by a constant (for example, multiply the first equation by 3 and the second equation by 2 to create a 6a term in both equations). But substitution wouldn’t be stellar in this situation, either. Note that combination may be particularly effective when the SAT asks for a variable expression. For example, if a question based on the previous system of equations asked for the value of 5a + 8b, then you could find the answer instantly by adding the equations together.
What does it mean if a system of equations has no solution? Infinitely many solutions?
A system of equations with no solution represents two parallel lines, which never cross. The coefficient of a variable in one equation will match the coefficient of the same variable in the other equation, but the constants will be different. For example, this system has no solution:
2x + 3y = 4
2x + 3y = 5
Subtracting one equation from the other yields the equation 0 = −1, which makes no sense.
If a system of equations has infinitely many solutions, then the two equations represent the same line. For example, this system has infinitely many solutions:
2x + 3y = 4
4x + 6y = 8
Dividing the second equation by 2 yields 2x + 3y = 4, so although the two equations look different, they are actually the same.Page 84
Next Steps
If you answered most questions correctly in the “How Much Have You Learned?” section, and if your responses to the Reflect questions were similar to those of the SAT expert, then consider Systems of Equations an area of strength and move on to the next chapter. Come back to this topic periodically to prevent yourself from getting rusty.
If you don’t yet feel confident, review those parts of this chapter that you have not yet mastered. In particular, review the mechanics for solving a system of equations by substitution and by combination. Then try the questions you missed again. As always, be sure to review the explanations closely.Page 85
Answers and Explanations
Substitution
-
1
Difficulty: Medium
Getting to the Answer: Start by isolating c in the second equation: c = 3b − 2. Then substitute into the first equation and solve:

Grid in 1.
-
A
Difficulty: Easy
Getting to the Answer: The quickest way to solve is to realize that you can rearrange the first equation to find that x = y. Then substitute y in for x in the second equation: y = 2y + 5. Solve to find that y = −5. Because x = y, x also equals −5, and x + y = −10. (A) is correct.
-
C
Difficulty: Medium
Getting to the Answer: Because x has a coefficient of 1 in the second equation, solve the system using substitution. Before you select your answer, make sure you found the right quantity (the difference between x and y).
First, solve the second equation for x and substitute:

Next, substitute this value back into x = 2 + 5y and simplify:

Finally, subtract x – y to find the difference:

(C) is correct.
-
B
Difficulty: Medium
Getting to the Answer: It’s equally easy to solve the second equation for either variable. The question asks for
 , so solve for a and substitute to create an equation in only one variable:
, so solve for a and substitute to create an equation in only one variable:
So
 , and (B) is correct.
, and (B) is correct. -
A
Difficulty: Medium
Getting to the Answer: Set up two equations: one for the number of items sold and one for the money collected. Let N = the number of bags of nuts sold and G = the number of packages of granola bars sold.
The equation for the total items is N + G = 112.
The equation for the money collected is 1.25N + 1.75G = 160.
Even though this is a calculator question, quickly converting the second equation to fractions is an efficient way to save time and prevent an entry mistake:
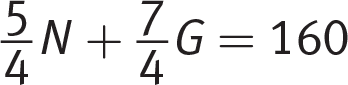 .
.Multiply by 4 to clear the equation of fractions to get 5N + 7G = 640.Page 86
At this point, you could solve by either combination or substitution. If you use substitution, solve the first equation for N, the number of bags of nuts, because the question asks for G, the number of packages of granola bars. Solving the first equation for N yields N = 112 − G.
Substituting that equation into the second equation gives:
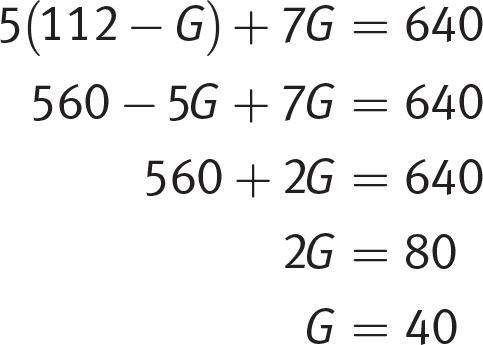
Remember the question asks for the number of cases of granola bars Marisol purchased, so divide 40 by 20, the number of packages of granola bars per case. (A) is correct.
As an alternative approach, if you read the question carefully and recognized you’re solving for the number of cases, not packages, the correct answer would have to be either (A) or (B), since (C) and (D) are way too big. You could then test one of those choices, say (A) 2, by multiplying by 20 packages of granola bars per case: 2 × 20 = 40. Subtract that number from 112 to get the number of bags of nuts: 112 − 40 = 72. Multiply each quantity by the price per package: 72 × 1.25 = 90 and 40 × 1.75 = 70. Then add the sales of the two items together: 90 + 70 = 160. You’ve now confirmed the correct answer because $160 is how much Marisol raised. If you had tested (B) instead, then you could have eliminated it and still arrived at the correct answer with no more work because you eliminated all choices except (A).
If you chose any of the other options, you likely answered the wrong question. (B) is the number of cases of nuts Marisol purchased, (C) is the number of packages of granola bars sold, and (D) is the number of bags of nuts sold.
Combination
-
25
Difficulty: Easy
Getting to the Answer: Often, when the SAT asks for a sum or difference of variables, solving by combination yields the answer very quickly. Add the equations:
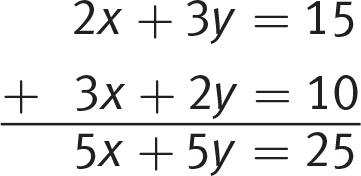
Grid in 25 and move on.
-
D
Difficulty: Easy
Getting to the Answer: This system is already set up perfectly to solve using combination because the y terms (−3y and 3y) are opposites. Add the two equations to cancel −3y and 3y. Then solve the resulting equation for x:
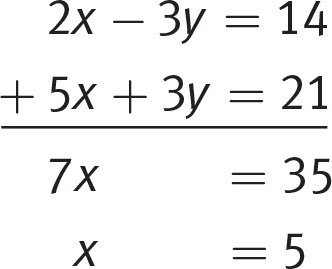
Choice (D) is correct. The question asks only for the value of x, so you don’t need to substitute x back into either equation to find the value of y.
-
D
Difficulty: Easy
Getting to the Answer: If you’re not asked to find the value of an individual variable, the question may lend itself to combination. This question asks for b + c, so don’t waste your time finding the variables individually if you can avoid it. After rearranging the equations so that variables and constants are aligned, you can add the equations together:

This matches (D).Page 87
-
59
Difficulty: Hard
Getting to the Answer: You’re asked for the value of an expression rather than the value of one of the variables, so try combination. Start by rearranging the two equations so that variables and constants are aligned:

Clear the fractions in the second equation and then add the equations:
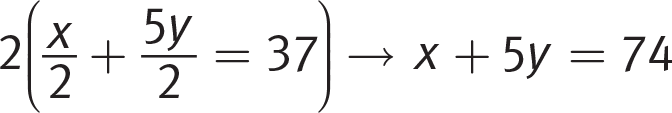
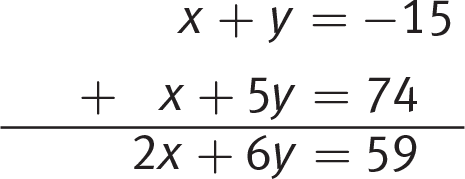
This is precisely what the question asks for, so you’re done. Grid in 59.
-

Difficulty: Medium
Getting to the Answer: None of the coefficients in either equation is 1, so using combination is a better strategy than substitution here. Examine the coefficients of x: they don’t share any factors, so multiply each equation by the coefficient from the other equation:
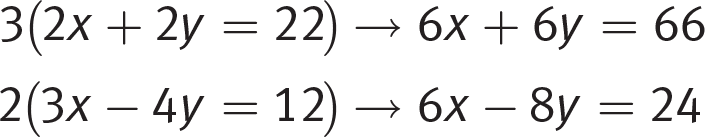
Subtract the second equation from the first:
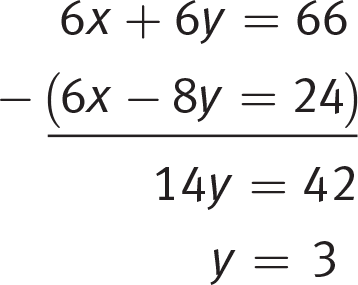
Next, you need x so you can determine the value of
 Substitute 3 for y in one of the original equations:
Substitute 3 for y in one of the original equations:
Plug your x- and y-values into
 to get
to get  . Grid in
. Grid in  .
.
Number of Possible Solutions
-
D
Difficulty: Medium
Strategic Advice: Note that (C) is impossible. There are only three possibilities: the lines intersect, in which case there is one solution; the lines are parallel, in which case there are no solutions; or the equations describe the same line, in which case there are infinitely many solutions.
Getting to the Answer: Get the two equations into the same format so that you can distinguish among these possibilities:

Now it’s easier to see that the first equation is equivalent to multiplying every term in the second equation by 6. Both equations describe the same line, so there are infinitely many solutions; (D) is correct.
-
B
Difficulty: Hard
Getting to the Answer: A system of equations that has infinitely many solutions describes a single line. Therefore, manipulation of one equation will yield the other. Look at the constant terms: to turn the 18 into a −2, divide the first equation by −9:

The y terms and constants in the second equation now match those in the first; all that’s left is to set the coefficients of x equal to each other:
 . Choice (B) is correct.
. Choice (B) is correct. Note that you could also write each equation in slope-intercept form and set the slopes equal to each other to solve for q.Page 88
-
C
Difficulty: Medium
Getting to the Answer: If the graphs intersect at (−3, 1), then the solution to the system is x = −3 and y = 1. Substitute these values into both equations and go from there:

So,
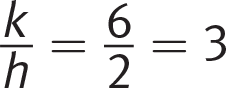 , making (C) correct.
, making (C) correct. -
B
Difficulty: Easy
Getting to the Answer: The solution to a system of linear equations represented graphically is the point of intersection. If the lines do not intersect, the system has no solution.
According to the graph, the lines intersect, or cross each other, at (6, 3). The question asks for the y-coordinate of the solution, which is 3, so (B) is correct.
-
D
Difficulty: Hard
Getting to the Answer: A system of linear equations has infinitely many solutions if both lines in the system have the same slope and the same y-intercept (in other words, they are the same line).
To have the same slope, the x- and y-coefficients of the two equations must be the same. Use the x-coefficients here: to turn
 into 3, multiply by 6. So c becomes 6c, and 6c = −6, or c = −1, which is (D).
into 3, multiply by 6. So c becomes 6c, and 6c = −6, or c = −1, which is (D).Note that you could also write each equation in slope-intercept form and set the y-intercepts equal to each other to solve for c.
-
B
Difficulty: Medium
Strategic Advice: The numbers here are fairly large, so substitution is not likely to be convenient. Moreover, the y-coefficients have the same absolute value, so combination will probably be the faster way to solve.
Getting to the Answer: Start by writing the second equation in the same form as the first, then use combination to solve for x:

Choice (B) is correct.
If you feel more comfortable using substitution, you can maximize efficiency by solving one equation for 5y and substituting that value into the other equation:

Note that the arithmetic is fundamentally the same, but the setup using combination is quicker and visually easier to follow.
-
D
Difficulty: Medium
Category: Combination
Strategic Advice: When a question asks for a sum or difference of variables, consider solving by combination.
Getting to the Answer: Rearrange the equations to be in the same form, with the y terms before the x terms, and then add:

The correct answer is (D).Page 89
-
C
Difficulty: Medium
Category: Substitution/Combination
Getting to the Answer: Because you’re given the variables (r for resident and n for nonresident), the only thing left for you to do is to break the wording apart into phrases and translate into math. Add together both student types to get the first equation: r + n = 1,980. This eliminates (A) and (D). Residents pay $421 in fees (421r), which eliminates (B). Only (C) is left, so it has to be the answer.
-
C
Difficulty: Medium
Category: Substitution
Getting to the Answer: Write a system of equations where c = the cost of the chair in dollars and s = the cost of the sofa in dollars. A sofa costs $50 less than three times the cost of the chair, or s = 3c − 50; together, a sofa and a chair cost $650, so s + c = 650.
The system is:

The top equation is already solved for s, so substitute 3c − 50 into the bottom equation for s and solve for c:
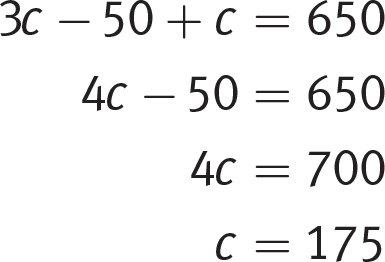
Remember to check if you solved for the right thing! The chair costs $175, so the sofa costs 3(175) − 50 = 525 − 50 = $475. This means the sofa costs $475 − $175 = $300 more than the chair. Therefore, (C) is correct.
-
8
Difficulty: Medium
Category: Number of Possible Solutions
Strategic Advice: The solution to the system is the point that both tables will have in common, but the tables, as given, do not share any points. You could use the data to write the equation of each line and then solve the system, but this will use up valuable time on test day. Instead, look for patterns that can be extended.
Getting to the Answer: In the table for Equation 1, the x-values increase by 2 each time and the y-values decrease by 2. In the table for Equation 2, the x-values increase by 4 each time and the y-values increase by 1. Use these patterns to continue the tables.
Equation 1 x y −2 6 0 4 2 2 4 0 6 −2 8 −4 Equation 2 x y −8 −8 −4 −7 0 −6 4 −5 8 −4 12 −3 The point (8, −4) satisfies both equations, so the x-coordinate of the solution to the system is 8.Page 90
-
A
Difficulty: Easy
Category: Number of Possible Solutions
Getting to the Answer: The solution to a system of equations shown graphically is the point of intersection. Read the axis labels carefully. Each grid line represents 2 units. The two lines intersect at the point (−6, −6), so A + B = −6 + (−6) = −12, which means (A) is correct.
-
C
Difficulty: Hard
Category: Number of Possible Solutions
Getting to the Answer: The system has infinitely many solutions, so both equations must describe the same line. Notice that if you multiply the x- and y-coefficients in the second equation by 8, you arrive at the x- and y-coefficients in the first equation. The constant k times 8 must then equal the constant in the first equation, or −16:
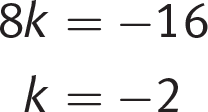
The correct answer is (C).
-
B
Difficulty: Hard
Category: Number of Possible Solutions
Getting to the Answer: Rearrange the equations and write them on top of each other so that the x and y variables line up:

In a system of equations that has no solution, the x-coefficients must equal each other and the y-coefficients must equal each other. Thus, for the x-coefficients, 24 = 6b , which means that b = 4. For the y-coefficients, a = −5. The question asks for the value of |a + b|, which is |−5 + 4| = |−1| = 1, choice (B). (Note that if you used the equation -6bx + 5y = 9, you would get a = 5 and b = -4, which would still result in the correct answer.)
-
 or 4.5
or 4.5Difficulty: Medium
Category: Substitution/Combination
Getting to the Answer: Start by clearing the fractions from the first equation (by multiplying by 4) to make the numbers easier to work with. Then use combination to solve for y:

Take half of 9 to get
 , then grid in 9/2 or 4.5.
, then grid in 9/2 or 4.5. -
A
Difficulty: Medium
Category: Substitution/Combination
Getting to the Answer: Choose intuitive letters for the variables: t for tiny pandas, g for giant pandas. You’re given the cost of each as well as the number of each sold and the total revenue generated. Then write the system of equations that represents the information given:

Multiplying the top equation by −14 allows you to solve for t using combination:

Solving for t gives 18, which eliminates (B) and (C). Plugging 18 into t in the first equation allows you to find g, which is 11. Choice (A) is correct.Page 91
-
A
Difficulty: Hard
Category: Substitution/Combination
Getting to the Answer: Choose letters that make sense for the variables: w for wooden and c for crystal. You know the jewelry artist bought 127 beads total. You’re also told each wooden bead costs $0.20 (0.2w) and each crystal bead costs $0.50 (0.5c), as well as the fact that she spent $41 total. You’ll have two equations: one relating the number of wooden beads and crystal beads and a second relating the costs associated with each:

Either combination or substitution is a good choice for solving this system. Both are shown here:
Combination:

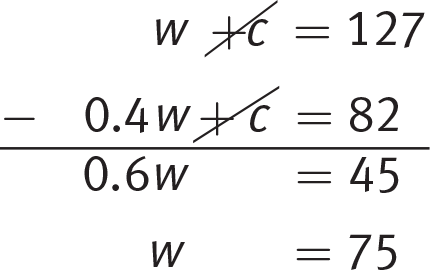
Substitution:
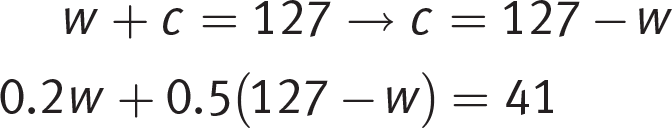


The question asks for the difference in the amount spent on each type of bead, not the difference in the quantity of each type. Multiply the bead counts by the correct pricing to get 75 × $0.2 = $15 for the wooden beads and 52 × $0.5 = $26 for the crystal beads. Take the difference to get $26 − $15 = $11, which is (A).