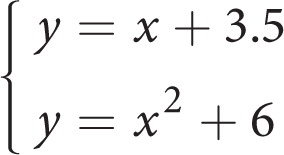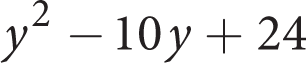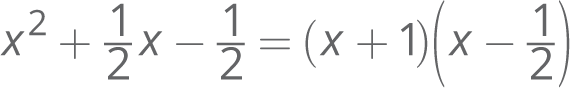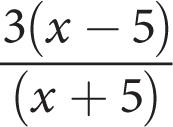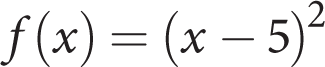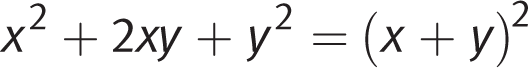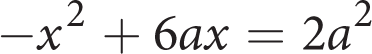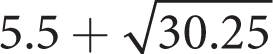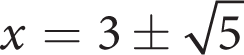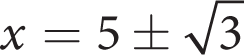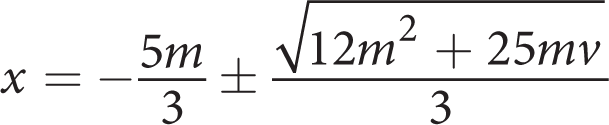Chapter 12
Quadratics
Page 320
How Much Do You Know?
Directions: Try the questions that follow. Show your work so that you can compare your solutions to the ones found in the Check Your Work section immediately after this question set. The “Category” heading in the explanation for each question gives the title of the lesson that covers how to solve it. If you answered the question(s) for a given lesson correctly, and if your scratchwork looks like ours, you may be able to move quickly through that lesson. If you answered incorrectly or used a different approach, you may want to take your time on that lesson.
- Which of the following linear expressions divides evenly into 6x 2 + 7x − 20 ?
- 3x − 10
- 3x − 5
- 3x − 4
- 3x − 2
-
x2 − 10x − 7
-
Which of the following expressions is equivalent to the expression above?
- (x − 5)2 − 32
- (x − 5)2 + 32
- (x + 5)2 − 32
- (x + 5)2 + 32
-
3x2 − 5x = −k
-
In the equation above, k is a constant. For which of the following values of k does the equation have at least one real solution?
- 2
- 3
- 4
- 5
-
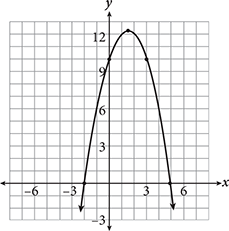
Which of the following could be the equation of the graph shown?
-
The x-coordinates of the solutions to a system of equations are 3.5 and 6. Which of the following could be the system?
Page 322
Check Your Work
-
C
Difficulty: Medium
Category: Solving Quadratics by Factoring
Getting to the Answer: Understanding that in algebra “divides evenly” means “is a factor” is the key to answering the question. You could use polynomial long division, but in most cases, factoring is quicker. The leading coefficient of the equation is not 1, so you’ll need to use grouping to factor the equation. The general form of a quadratic is ax2 + bx + c. To find the factors, multiply a by c, 6 × −20 = −120, and then look for two factors of that product whose sum is equal to b, the coefficient of the middle term. The two factors of −120 that add up to 7 are 15 and −8:

Therefore, 3x − 4 divides evenly into the expression, so (C) correct.
-
A
Difficulty: Medium
Category: Completing the Square
Getting to the Answer: There are no integer factors of x2 − 10x − 7, since no two integers whose product is −7 add up to −10. Note that the answer choices are stated in vertex format, the same as you would obtain by completing the square of the given expression. Half of the x-coefficient, −10, is −5, so the constant term needed to complete the square is (−5)2 = 25. Thus, you can rewrite and group the given expression as (x2 − 10x + 25) − 25 − 7. This simplifies to (x − 5)2 − 32, which is (A). Noticing that x2 − 10x + 25 is a classic quadratic makes the process of factoring very quick.
-
A
Difficulty: Medium
Category: The Quadratic Formula
Getting to the Answer: Restate the equation in “standard” quadratic form, 3x2 − 5x + k = 0. Recall that a quadratic equation has two real solutions if the discriminant, b2 − 4ac, is positive. The equation has one real solution if the discriminant is 0. For the given equation, a = 3, b = −5, and c = k, so you can set up the inequality (−5)2 − 4(3)k ≥ 0 . This simplifies to 25 ≥ 12k. The only choice for which this is true is (A).
If you didn’t recall the shortcut about the discriminant, consider the quadratic formula,
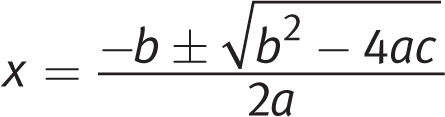 . If the term inside the radical, b2 − 4ac, is negative, then there are no real solutions.
. If the term inside the radical, b2 − 4ac, is negative, then there are no real solutions. -
D
Difficulty: Easy
Category: Graphs of Quadratics
Getting to the Answer: The graph is a parabola, so you can eliminate (A) because its equation is linear. The x‑intercepts of the graph are −2 and 5, so the factors of the quadratic are (x + 2) and (x − 5). These factors make y = 0 when x = −2 and x = 5. Eliminate (B) and (C). Only (D) is left, so it must be correct. On test day, you would move on. For the record, the parabola opens downward, so there should be a negative sign in front of the factors. (D) is correct.Page 323
-
C
Difficulty: Hard
Category: Systems of Quadratic and Linear Equations
Getting to the Answer: You don’t actually need to solve each system. Instead, plug 3.5 or 6 into each answer choice and eliminate each one whose y-values don’t come out the same. (If the same x-value produces different y-values in two equations, then it is not the x-coordinate of the solution to the system.) Because 3.5 is a decimal, doing arithmetic with it is likely to be messy. So start with 6:
(A): y = 6 + 3.5 = 9.5
y = 6² + 6 = 36 + 6 = 42
Different y-values; eliminate.(B): y = 2(6) − 7 = 12 − 7 = 5
y = −(6 − 6)² = −(0)² = 0 Different y-values; eliminate.(C):

y = −(6 − 5)² + 7 = −(1)² + 7 = −1 + 7 = 6Keep for now. You need to test (D) because it’s possible that (D) is the right answer and (C) just happens to work for x = 6 (but not for x = 3.5).
(D):

y = −(6 − 6)² + 3.5 = −(0)² + 3.5 = 3.5 Different y-values; eliminate.(C) is correct.
Page 324
Solving Quadratics by Factoring
To answer a question like this:
-
If x 2 − 7x = 30 and x > 0, what is the value of x − 5 ?
- 5
- 6
- 10
- 25
You need to know this:
A quadratic expression is a second-degree polynomial—that is, a polynomial containing a squared variable. You can write a quadratic expression as  .
.
The FOIL acronym (which stands for First, Outer, Inner, Last) will help you remember how to multiply two binomials: multiply the first terms together (ac), then the outer terms (ad), then the inner terms (bc), and finally the last terms (bd):
(a + b)(c + d) = ac + ad + bc + bd
FOIL can also be done in reverse if you need to go from a quadratic to its factors.
To solve a quadratic equation by factoring, the quadratic must be set equal to 0. For example:

From the binomial factors, you can find the solutions, also called roots or zeros, of the equation. For two factors to be multiplied together and produce zero as the result, one or both those factors must be zero. In the example above, either x + 8 = 0 or x − 7 = 0, which means that x = −8 or x = 7.
You need to do this:
Here are the steps for solving a quadratic equation by factoring:
- Set the quadratic equal to zero.
- Factor the squared term. (For factoring, it’s easiest when a, the coefficient in front of x 2, is equal to 1.)
- Make a list of the factors of c. Remember to include negatives.
- Find the factor pair that, when added, equals b, the coefficient in front of x.
- Write the quadratic as the product of two binomials.
- Set each binomial equal to zero and solve.
Page 325
Explanation:
Set the equation equal to zero and factor the first term:
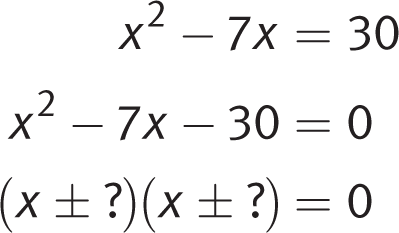
Next, consider factors of −30, keeping in mind that they must sum to −7, so the factor with the greater absolute value must be negative. The possibilities are: −30 × 1, −15 × 2, −10 × 3, and −6 × 5. The factor pair that sums to −7 is −10 × 3. Write that factor pair into your binomials:

Set each factor equal to zero and solve:

The question says that x > 0, so x = 10. Now that you solved for x, you can answer the question, which asks for x − 5: 10 − 5 = 5. (A) is correct.
If factoring quadratics gives you trouble, study the steps in the table above and try these Drill questions before completing the following Try on Your Own questions. Factor each quadratic expression (without using a calculator). Turn the page to see the answers.
Drill
Solving Quadratics By Factoring Drill Answers
Page 326
Try on Your Own
Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.
-
Which of the following is an equivalent form of the expression (6 − 5x)(15x − 11) ?
- −75x 2 + 35x − 66
- −75x 2 + 145x − 66
- 90x 2 − 141x + 55
- 90x 2 + 9x + 55
-
Which of the following is equivalent to
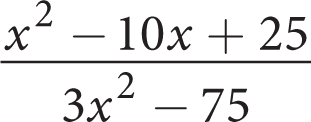 ?
? -
For what positive value of x is the equation
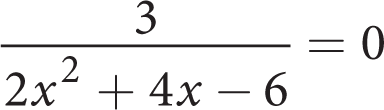 undefined?
undefined?
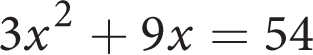
-
What is the sum of the roots of the equation above?
- −6
- −3
- 3
- 6

-
Which of the following functions is equivalent to the function above?
Classic Quadratics
To answer a question like this:
-
Which of the following expressions is equivalent to 25x 2y 4 − 1 ?
- 5(x 2y 4 − 1)
- −5(xy 2 + 1)
- (5xy −1)(5xy + 1)
- (5xy 2 − 1)(5xy 2 + 1)
You need to know this:
Memorizing the following classic quadratics will save you time on test day:
You need to do this:
When you see a pattern that matches either the left or the right side of one of the above equations, simplify by substituting its equivalent form. For example, say you need to simplify the following:

You would substitute (a − b)(a − b) for the numerator and cancel to find that the expression simplifies to a − b:

Explanation:
The expression  is a difference of perfect squares. It corresponds to the first of the three classic quadratic patterns above. The square root of
is a difference of perfect squares. It corresponds to the first of the three classic quadratic patterns above. The square root of  is
is  and the square root of 1 is 1, so the correct factors are
and the square root of 1 is 1, so the correct factors are  . Choice (D) is correct.Page 329
. Choice (D) is correct.Page 329
Try on Your Own
Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.
-
For all a and b, what is the sum of (a − b)2 and (a + b)2 ?
- 2a2
- 2a2 − 2b2
- 2a2 + 2b2
- 2a2 + 4ab + 2b2
-
What is the positive difference between the roots of the equation
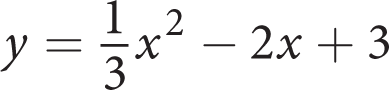 ?
?
-

-
For which value of x is the function f(x) undefined?

-
Suppose
 and
and  . Assuming c > 0, what is the value of a ?
. Assuming c > 0, what is the value of a ?

-
In the expression above, a > 1 and both a and b are constants. Which of the following could be the value of b ?
- −7
- 7
- 14
- 49
Page 330
Completing the Square
To answer a question like this:
-
Which of the following equations has the same solutions as the equation 40 − 6x = x2 − y ?
- y = (x − 6)2 − 40
- y = (x − 6)2 + 40
- y = (x + 3)2 − 49
- y = (x + 3)2 + 49
You need to know this:
For quadratics that do not factor easily, you’ll need one of two strategies: completing the square or the quadratic formula (taught in the next lesson). To complete the square, you’ll create an equation in the form (x + h)2 = k, where h and k are constants.
As with factoring, completing the square is most convenient when the coefficient in front of the x2 term is 1.
You need to do this:
Here are the steps for completing the square, demonstrated with a simple example.
| Step | Scratchwork |
|---|---|
| Starting point: | x 2 + 8x − 8 = 0 |
| 1. Move the constant to the opposite side. | x 2 + 8x = 8 |
| 2. Divide b, the x-coefficient, by 2 and square the quotient. |

|
| 3. Add the number from the previous step to both sides of the equation and factor. |
x 2 + 8x + 16 = 8 + 16
(x + 4)(x + 4) = 24 (x + 4)2 = 24 |
| 4. Take the square root of both sides. |

|
| 5. Split the result into two equations and solve each one. | 
|
Page 331
Explanation:
First, write the equation in standard form: y = x 2 + 6x − 40. Add 40 to both sides and complete the square on the right-hand side. Find  , and add the result to both sides of the equation:
, and add the result to both sides of the equation:
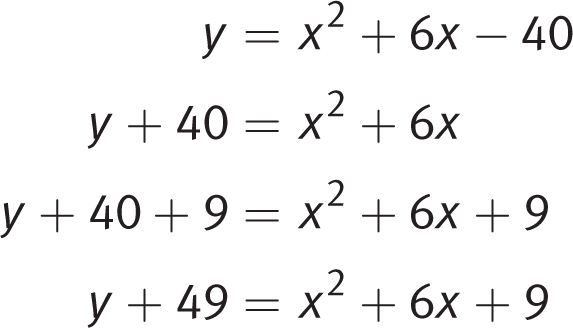
Note that all of the answer choices are in factored form. The right side of the equation is a classic quadratic that factors as follows:
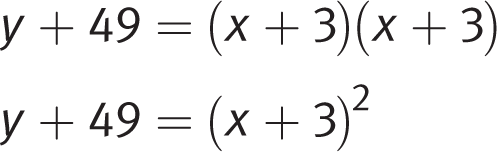
Finally, solve for y to get y = (x + 3)2 − 49, which means (C) is correct.
If you find completing the square to be challenging, study the steps in the table above and try these Drill questions before completing the following Try on Your Own questions. Turn the page to see the answers.
Drill
Completing The Square Drill Answers
Page 332
Try on Your Own
Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.
-
Which of the following is a value of x that satisfies the equation x 2 + 2x − 5 = 0 ?
- −1



-

-
Which of the following is the greatest possible value of a ?


- 12

-
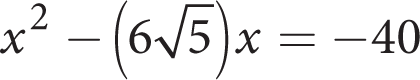
-
What is the sum of the possible values of x given the above equation?
- 15
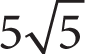

- 60

-
Which of the following is a value of x that is valid in the above equation?
Page 333
The Quadratic Formula
To answer a question like this:
-
Which of the following are the real values of x that satisfy the equation 2x 2 − 5x − 2 = 0 ?
- 1 and 4
 and
and 
 and
and 
- No real solutions
You need to know this:
The quadratic formula can be used to solve any quadratic equation. It yields solutions to a quadratic equation that is written in standard form, ax 2 + bx + c = 0:
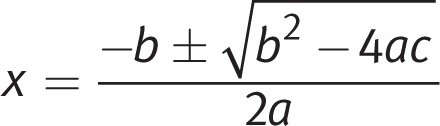
The ± sign that follows −b indicates that you will have two solutions, so remember to find both.
The expression under the radical (b2 − 4ac) is called the discriminant, and its value determines the number of real solutions. If the discriminant is positive, the equation has two distinct real solutions. If the discriminant is equal to 0, there is only one distinct real solution. If the discriminant is negative, there are no real solutions because you cannot take the square root of a negative number.
The arithmetic can get complicated, so reserve the quadratic formula for equations that cannot be solved by factoring and those in which completing the square is difficult because  .
.
You need to do this:
Get the quadratic equation into the form ax 2 + bx + c = 0. Then substitute a, b, and c into the quadratic formula and simplify.Page 334
Explanation:
In the given equation, a = 2, b = −5, and c = −2. Plug these values into the quadratic formula and simplify:

The correct answer is (C).
If you find the quadratic formula to be challenging, study the formula and try these Drill questions before completing the following Try on Your Own questions. Turn the page to see the answers.
Drill
The Quadratic Formula Drill Answers
Page 335
Try on Your Own
Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.
-
Given the equation 2x2 + 8x + 4 + 2z = 0, for what value of z is there exactly one solution for x ?

-
The product of all the solutions to the equation 3v2 + 4v – 2 = 0 is M. What is the value of M ?
- –3



-
What are the solutions to the equation 4x2 – 24x + 16 = 0 ?
-
3x2 = m(5x + v)
-
What are the values of x that satisfy the equation above, where m and v are constants?
-
-
x(dx + 10) = −3
-
-
The equation above, where d is a constant, has no real solutions. The value of d could be which of the following?
- –12
- 4
- 8
- 10
-
Which of the following equations does NOT have any solutions that are real numbers?
- x2 + 8x − 12 = 0
- x2 − 8x + 12 = 0
- x2 − 9x + 21 = 0
- x2 + 100x − 1 = 0
Page 336
Graphs of Quadratics
To answer a question like this:
-
Given the equation y = −(2x − 4)2 + 7, which of the following statements is NOT true?
- The vertex is (4, 7).
- The y-intercept is (0, −9).
- The parabola opens downward.
- The graph crosses the x-axis at least one time.
You need to know this:
A quadratic function is a quadratic equation set equal to y or f (x) instead of 0. Remember that the solutions (also called “roots” or “zeros”) of any polynomial function are the same as the x-intercepts. To solve a quadratic function, substitute 0 for y, or f (x), then solve algebraically. Alternatively, you can plug the equation into your graphing calculator and read the x-intercepts from the graph.
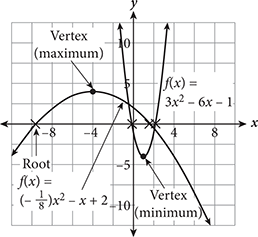
The graph of every quadratic equation (or function) is a parabola, which is a symmetric U-shaped graph that opens either upward or downward. To determine which way a parabola will open, examine the value of a in the equation. If a is positive, the parabola will open upward. If a is negative, it will open downward. Take a look at the examples above to see this graphically.Page 337
Like quadratic equations, quadratic functions will have zero, one, or two distinct real solutions, corresponding to the number of times the parabola touches or crosses the x-axis. Graphing is a powerful way to determine the number of solutions a quadratic function has.
| Two Real Solutions | One Real Solution | No Real Solutions |
|---|---|---|
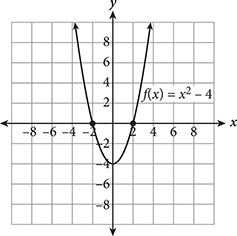
|

|
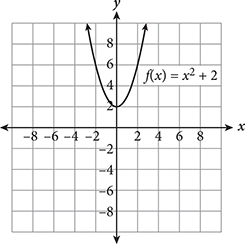
|
There are three algebraic forms that a quadratic equation can take: standard, factored, and vertex. Each is provided in the following table along with the graphical features that are revealed by writing the equation in that particular form.
| Standard | Factored | Vertex |
|---|---|---|
| y = ax2 + bx + c | y = a(x − m)(x − n) | y = a(x − h)2 + k |
| y-intercept is c | Solutions are m and n | Vertex is (h, k) |
| In real-world contexts, starting quantity is c | x-intercepts are m and n | Minimum/maximum of function is k |
| Format used to solve via quadratic formula | Vertex is halfway between m and n | Axis of symmetry is given by x = h |
You’ve already seen standard and factored forms earlier in this chapter, but vertex form might be new to you. In vertex form, a is the same as the a in standard form, and h and k are the coordinates of the vertex(h, k). If a quadratic function is not in vertex form, you can still find the x-coordinate of the vertex by plugging the appropriate values into the equation  , which is also the equation for the axis of symmetry (see graph that follows). Once you determine h, plug this value into the quadratic function and solve for y to determine k, the y-coordinate of the vertex.Page 338
, which is also the equation for the axis of symmetry (see graph that follows). Once you determine h, plug this value into the quadratic function and solve for y to determine k, the y-coordinate of the vertex.Page 338
The equation of the axis of symmetry of a parabola is x = h, where h is the x-coordinate of the vertex.
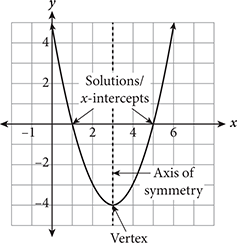
You need to do this:
- To find the vertex of a parabola, get the function into vertex form: y = a(x − h)2 + k or use the formula
 .
. - To find the y-intercept of a quadratic function, plug in 0 for x.
- To determine whether a parabola opens upward or downward, look at the coefficient of a. If a is positive, the parabola opens upward. If negative, it opens downward.
- To determine the number of x-intercepts, set the quadratic function equal to 0 and solve or examine its graph. (Quadratic function questions show up on both the no-calculator and calculator sections of the SAT.)
Explanation
Be careful—the equation looks like vertex form, y = a(x − h)2 + k, but it’s not quite there because of the 2 inside the parentheses. You could rewrite the equation in vertex form, but this would involve squaring the quantity in parentheses and then completing the square, which would take quite a bit of time. Alternatively, you could notice that the greatest possible value for y in this function is 7, which happens when the squared term, −(2x − 4)2, equals zero. To check (A), find the x-value when y = 7:

For the record:
Choice (B): Substitute 0 for x and simplify to find that the y-intercept is indeed (0, −9).
Choice (C): There is a negative in front of the squared term, so the parabola does open downward.
Choice (D): Because the parabola opens downward and the vertex is at y = 7, above the x-axis, the parabola must cross the x-axis twice. This statement is true as well, which confirms that (A) is correct.Page 339
Try on Your Own
Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.
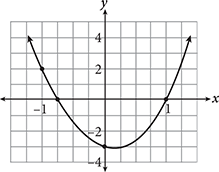
-
The following quadratic equations are all representations of the graph above. Which equation clearly represents the exact values of the x-intercepts of the graph?
- y = 4x 2 − x − 3
- y = (4x + 3)(x − 1)
- y = 4(x − 0.125)2 − 3.0625
- y + 3.0625 = 4(x − 0.125)2
-
Which equation represents the axis of symmetry for the graph of the quadratic function
 ?
? -
How many times do the parabolas given by the equations f(x) = 3x2 − 24x + 52 and g(x) = x2 + 12x − 110 intersect?
- Never
- Once
- Twice
- More than twice
-
What is the positive difference between the x-intercepts of the parabola given by the equation g(x) = −2.5x 2 + 10x − 7.5 ?

-
A toy rocket is fired from ground level. The height of the rocket with respect to time can be represented by a quadratic function. If the toy rocket reaches a maximum height of 34 feet 3 seconds after it was fired, which of the following functions could represent the height, h, of the rocket t seconds after it was fired?
- h(t) = −16(t − 3)2 + 34
- h(t) = −16(t + 3)2 + 34
- h(t) = 16(t − 3)2 + 34
- h(t) = 16(t + 3)2 + 34
Page 340
Systems of Quadratic and Linear Equations
To answer a question like this:
-
In the xy-plane, the graph of
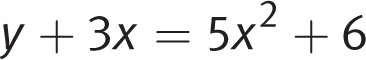 and
and  intersect at points (0, 6) and (a, b). What is the value of b ?
intersect at points (0, 6) and (a, b). What is the value of b ?
You need to know this:
You can solve a system of one quadratic and one linear equation by substitution, exactly as you would for a system of two linear equations. Alternatively, if the question appears on the calculator section, you can plug the system into your graphing calculator.
You need to do this:
- Isolate y in both equations
- Set the equations equal to each other
- Put the resulting equation into the form

- Solve this quadratic by factoring, completing the square, or using the quadratic formula. (You are solving for the x-values at the points of intersection of the original two equations.)
- Plug the x-values you get as solutions into one of the original equations to generate the y-values at the points of intersection. (Usually, the linear equation is easier to work with than the quadratic.)
Page 341
Explanation:
Start by isolating y in both equations to get  and
and  . Next, set the right sides of the equations equal and solve for x:
. Next, set the right sides of the equations equal and solve for x:

The question says that (0, 6) is one point of intersection for the two equations and asks for the y-value at the other point of intersection, so plug x = 1 into either of the original equations and solve for y. Using the linear equation will be faster:

Therefore, the point (a, b) is (1, 8). Grid in 8.Page 342
Try on Your Own
Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be an opportunity for timed practice at the end of the chapter.

-
The ordered pair (a, b) satisfies the system of equations above. What is one possible value of b ?
- –6
- –3
- 2
- 3
-
In the xy-coordinate plane, the graph of
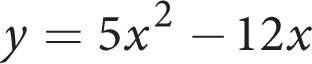 intersects the graph of y = –2x at points (0, 0) and (a, b). What is the value of a ?
intersects the graph of y = –2x at points (0, 0) and (a, b). What is the value of a ?
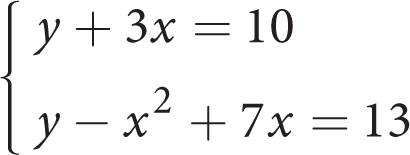
-
How many real solutions are there to the system of equations above?
- Exactly 4 real solutions
- Exactly 2 real solutions
- Exactly 1 real solution
- No real solutions

-
The graph of the function f, defined by f(x) = –2(x – 3)2 – 4, is shown in the xy-plane above. The function g (not shown) is defined by g(x) = 2x – 10. If f(c) = g(c), what is one possible value of c ?
- –6
- –4
- 2
- 4
Page 343
-
On the xy-plane, points P and Q are the two points where the parabola with the equation
 and the line with the equation
and the line with the equation  meet. What is the distance between point P and point Q ?
meet. What is the distance between point P and point Q ?- 5
- 8
- 10
- 12
Page 344
How Much Have You Learned?
Directions: For testlike practice, give yourself 18 minutes to complete this question set. Be sure to study the explanations, even for questions you got right. They can be found at the end of this chapter.
-
The equation
 has two solutions: x = −5 and x = 7. What is the value of 2k ?
has two solutions: x = −5 and x = 7. What is the value of 2k ?
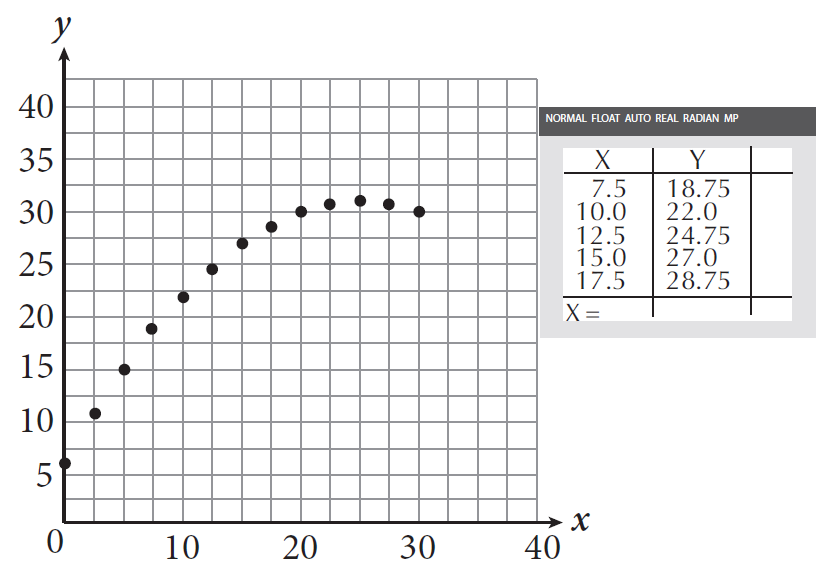
-
The maximum value of the data shown in the scatterplot above occurs at x = 25. If the data is modeled using a quadratic regression and the correlation coefficient is 1.0 (the fit is exact), then what is the y-value when x = 35 ?
- 10
- 15
- 22
- 27
-
-
Questions 34 and 35 refer to the following information.
-
The height of a boulder launched from a Roman catapult can be described as a function of time according to the following quadratic equation: h(t) = −16t 2 + 224t + 240.
-
What is the maximum height that the boulder attains?
- 240
- 784
- 1,024
- 16,96
-
How much time elapses between the moment the boulder is launched and the moment it hits the ground, assuming that the ground is at a height of 0 ?
- 7
- 12
- 14
- 15
- Page 346
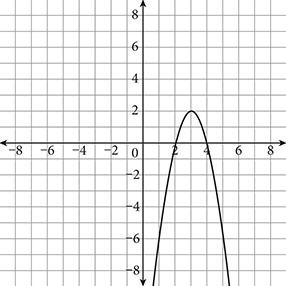
-
-
If the function shown in the graph is represented by f(x) = a(x − h)2 + k, which of the following statements is NOT true?
- The value of a is negative.
- f (x) is symmetrical across the line y = 3.
- The function
 intersects f (x) at its vertex.
intersects f (x) at its vertex. - The value of h is positive.
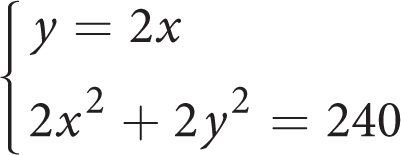
-
If (x, y) is a solution to the system of equations above, what is the value of x 2 ?

-
What are the x-intercepts of the parabolic function
 ?
? and
and 
- 1 and

 and
and 
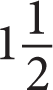 and
and 
-
If g(x) = (x − 2)2 − 5, which of the following statements is true?
- The function g(x) is increasing over the entire domain.
- The function g(x) is decreasing over the entire domain.
- The function g(x) is increasing for x < 2 and decreasing for x > 2.
- The function g(x) is decreasing for x < 2 and increasing for x > 2.
-
What is the sum of the solutions of (6x + 5)2 − (3x − 2)2 = 0 ?



- 3

-
If the equation above is true, then what is the positive value of the expression
 ?
?- 20
- 25
- 30
- 35
Page 347
-
In the equation
 , which of the following is a possible value of x − 2 ?
, which of the following is a possible value of x − 2 ?
- 2

- 3
-
If
 , x and y are positive integers, and x > y, what is the value of x − y ?
, x and y are positive integers, and x > y, what is the value of x − y ?- 1
- 2
- 3
- 8
Page 348
Reflect
Directions: Take a few minutes to recall what you’ve learned and what you’ve been practicing in this chapter. Consider the following questions, jot down your best answer for each one, and then compare your reflections to the expert responses on the following page. Use your level of confidence to determine what to do next.Page 349
What features in a quadratic equation should you look for to decide whether to factor, complete the square, or apply the quadratic formula?
Which constant in the vertex form of a quadratic function gives its maximum or minimum?
Which form of a quadratic equation gives its y-intercept?
Which form of a quadratic equation gives its x-intercepts, assuming the equation has two real roots?
How do you solve a system of one linear and one quadratic equation?
Expert Responses
What features in a quadratic equation should you look for to decide whether to factor, complete the square, or apply the quadratic formula?
Get the equation into standard form. If the coefficient in front of the squared term is 1, try factoring, but don’t spend longer than about 15 seconds on the attempt. If you can’t get the quadratic factored quickly, look at the coefficient on the middle term: if it is even, completing the square will be an efficient approach. Finally, the quadratic formula will work for any quadratic, no matter what the coefficients are.
Which constant in the vertex form of a quadratic function gives its maximum or minimum?
The vertex form is
 . The constant k is the y‑value at the vertex, which occurs at the maximum or minimum.
. The constant k is the y‑value at the vertex, which occurs at the maximum or minimum.
Which form of a quadratic equation gives its y-intercept?
The standard form,  . The y-intercept is given by c.
. The y-intercept is given by c.
Which form of a quadratic equation gives its x-intercepts, assuming the equation has two real roots?
The factored form,  . The x-intercepts are at x = m and x = n.
. The x-intercepts are at x = m and x = n.
How do you solve a system of one linear and one quadratic equation?
Put the linear equation in the form  and the quadratic in the form
and the quadratic in the form  . Set the right sides of the equations equal to each other and solve.
. Set the right sides of the equations equal to each other and solve.
Next Steps
If you answered most questions correctly in the “How Much Have You Learned?” section, and if your responses to the Reflect questions were similar to those of the SAT expert, then consider quadratics an area of strength and move on to the next chapter. Come back to this topic periodically to prevent yourself from getting rusty.
If you don’t yet feel confident, review those parts of this chapter that you have not yet mastered. In particular, study the table describing the different forms of quadratics in the Graphs of Quadratics lesson. Then try the questions you missed again. As always, be sure to review the explanations closely.Page 350
Answers and Explanations
Try on Your Own
-
B
Difficulty: Easy
Getting to the Answer: FOIL the binomials (6 − 5x)(15x − 11): First, Outer, Inner, Last. First: (6)(15x) = 90x. Outer: (6)(−11) = −66. Inner: (−5x)(15x) = −75x 2. Last: (−5x)(−11) = 55x. Add all the terms together and combine like terms: 90x − 66 − 75x 2 + 55x = −75x 2 + 145x − 66. The correct answer is (B).
-
C
Difficulty: Easy
Getting to the Answer: First, factor out a 3 in the denominator to make that quadratic a bit simpler. Then factor the numerator and denominator using reverse-FOIL to reveal an x − 5 term that will cancel out:

The correct answer is (C).
-
1
Difficulty: Medium
Getting to the Answer: An expression is undefined when it involves division by 0, so the key to the problem is to recognize that the denominator will be 0 if either of the factors of the quadratic are zero. Factoring 2 out of the denominator leaves a relatively easy-to-factor quadratic:

The denominator will be zero if the value of x is either 1 or −3. Because the question asks for a positive value of x, grid in 1.
-
B
Difficulty: Medium
Getting to the Answer: Set the equation equal to zero, then divide through by 3 on both sides to remove the
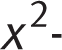 coefficient:
coefficient:
The question asks for the sum of the roots, which is 3 + (−6) = −3. The correct answer is (B).
-
A
Difficulty: Hard
Strategic Advice: The question asks for an equivalent expression, so ignore the function notation and focus on manipulating the polynomial into standard form so it matches most of the answer choices.
Getting to the Answer: Expand the polynomial and distribute as necessary so that all of the parentheses are eliminated:

Decimals are harder to work with than integers, so multiply by 100. Then combine like terms. Factor 100 back out and check to see if the result matches any of the answer choices:

Factor the polynomial:
 . (A) is correct.Page 351
. (A) is correct.Page 351
-
C
Difficulty: Easy
Getting to the Answer: Expand both classic quadratics and combine like terms to find the sum:

This matches (C).
-
0
Difficulty: Medium
Getting to the Answer: To find the roots, set the equation equal to 0, factor it, and then solve. Clear the fraction the same way you do when solving equations and multiply both sides of the equation by the denominator of the fraction:

The equation only has one unique solution (x = 3), so the positive difference between the roots is 3 − 3 = 0.
-
4
Difficulty: Hard
Getting to the Answer: A fraction is undefined when the denominator equals 0. To find the value of x where f(x) is undefined, set the denominator to 0 and solve for x.
The equation
 is the expansion of the classic quadratic
is the expansion of the classic quadratic  , where a = (x − 7) and b = 3, so the denominator will factor as
, where a = (x − 7) and b = 3, so the denominator will factor as  . That’s equivalent to
. That’s equivalent to  . Set this expression equal to zero to find that the function is undefined when x − 4 = 0, or x = 4.
. Set this expression equal to zero to find that the function is undefined when x − 4 = 0, or x = 4. -
4
Difficulty: Hard
Strategic Advice: Look for classic quadratics so you can avoid reverse-FOIL and save time:

Getting to the Answer: Recognize that a2 + 2ab + b2 is a classic quadratic that simplifies to (a + b)2. Factor the polynomial and take the square root of both sides to simplify the result:

The question says that c is positive. Subtracting b from both sides gives a = c − b. Plugging in 4 for c − b gives a = 4.
-
B
Difficulty: Medium
Strategic Advice: Recognizing the classic quadratic
 will save you time in factoring.
will save you time in factoring. Getting to the Answer: In this question, the goal is to manipulate the polynomial so that it matches the factored form given. First, recognize that 2, the coefficient of
 , can be factored out. The resulting expression is then
, can be factored out. The resulting expression is then  . Notice that
. Notice that  and factor the quadratic to get
and factor the quadratic to get  . Now the expression is in the same form as
. Now the expression is in the same form as 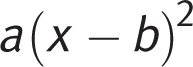 . Therefore, b = 7, so (B) is correct.Page 352
. Therefore, b = 7, so (B) is correct.Page 352
-
D
Difficulty: Medium
Getting to the Answer: Factoring won’t work here because no two factors of −5 sum to 2. However, the coefficient of x 2 is 1, so try completing the square:

(D) matches one of the two possible values of x, so it’s correct.
-
B
Difficulty: Hard
Getting to the Answer: Even though the given equation contains the value a4, this is a quadratic-style question. You can say that x = a2, so
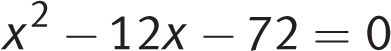 . To complete the square, restate this as
. To complete the square, restate this as  . One-half of the x-coefficient is 6, which, when squared, becomes 36. So,
. One-half of the x-coefficient is 6, which, when squared, becomes 36. So,  . Factor to find that (x − 6)2 = 108 and then take the square root of both sides to get
. Factor to find that (x − 6)2 = 108 and then take the square root of both sides to get  . Since 108 = 36 × 3, the radical simplifies to
. Since 108 = 36 × 3, the radical simplifies to  .
.Now substitute a2 back in for x:
 and
and  . Since the question asks for the root with the greatest value, you can ignore the root with the minus sign, so
. Since the question asks for the root with the greatest value, you can ignore the root with the minus sign, so  . Take the square root of both sides, and ignore the root with the negative sign to get
. Take the square root of both sides, and ignore the root with the negative sign to get  . (B) is correct.
. (B) is correct. -
C
Difficulty: Hard
Getting to the Answer: The radical looks as if it will make the calculation difficult, but it will drop out when you complete the square. The coefficient, b, is
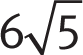 , so
, so 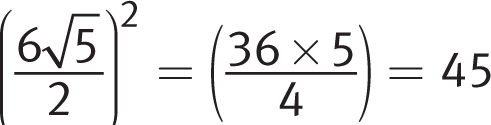 . Adding 45 to both sides of the equation gives you
. Adding 45 to both sides of the equation gives you  , so the factored form is
, so the factored form is  . Take the square root of both sides to get
. Take the square root of both sides to get  . The two possible values of x are
. The two possible values of x are  and
and  . The question asks for the sum of these values, which is
. The question asks for the sum of these values, which is  . (C) is correct.
. (C) is correct. -
A
Difficulty: Hard
Getting to the Answer: Subtract the left side of the equation from the right side: 0 = 2x2 − x2 − 4x − 7x + 3 − 1 = x2 − 11x + 2. Combine like-terms to get x2 − 11x = −2. So, b = −11, and
 . Thus, completing the square gives you x2 − 11x + 30.25 = 28.25. (This is a calculator-allowed question, so feel free to use the calculator if you need to do so. You could also have used the calculator to backsolve to find the correct choice.) Factor the left side to get (x − 5.5)2 = 28.25 and
. Thus, completing the square gives you x2 − 11x + 30.25 = 28.25. (This is a calculator-allowed question, so feel free to use the calculator if you need to do so. You could also have used the calculator to backsolve to find the correct choice.) Factor the left side to get (x − 5.5)2 = 28.25 and 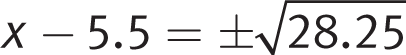 . Therefore, x can be either
. Therefore, x can be either 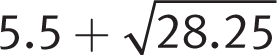 or
or 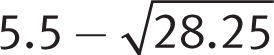 . The latter solution matches (A).
. The latter solution matches (A).
-
2
Difficulty: Hard
Strategic Advice: Recall that when the value of the discriminant, b2 − 4ac, is 0, there is exactly one solution to the quadratic equation.
Getting to the Answer: The given equation is 2x2 + 8x + 4 + 2z = 0, but there is a common factor of 2 in all the terms, so this becomes x2 + 4x + 2 + z = 0. So a = 1, b = 4, and c = 2 + z . Set the discriminant 42 − 4(1)(2 + z) equal to 0 so that there is only one solution. Expand the equation to 16 − 8 − 4z = 0. Thus, 8 = 4z, and z = 2. Grid in 2.
Page 353 -
B
Difficulty: Hard
Getting to the Answer: The question presents a quadratic equation that cannot be easily factored. Therefore, use the quadratic formula to solve. The quadratic formula states that
 .
. In this case, a = 3, b = 4, and c = −2. Plug in these values to get:
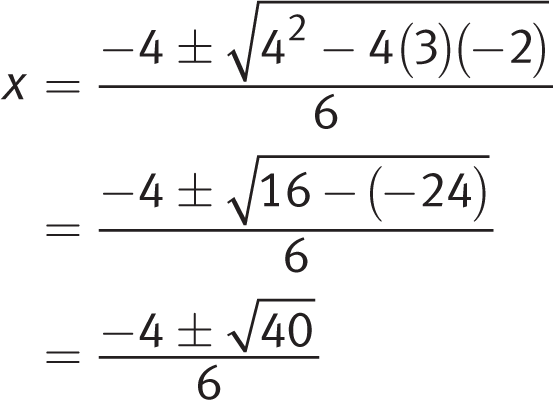
Thus, the solutions to the equation are
 and
and  . The question asks for their product:
. The question asks for their product: 
(B) is correct.
-
A
Difficulty: Medium
Strategic Advice: When all of the coefficients in a quadratic equation are divisible by a common factor, simplify the equation by dividing all terms by that factor before solving.
Getting to the Answer: The given equation is 4x2 – 24x + 16 = 0, but there is a common factor of 4 in all the terms, so this becomes x2 – 6x + 4 = 0. Therefore, a = 1, b = –6, and c = 4.
The radicals in the answer choices are a strong clue that the quadratic formula is the way to solve this equation. The quadratic formula is
 , and after you plug in the coefficients, you get:
, and after you plug in the coefficients, you get: 
This doesn’t resemble any of the answer choices, so continue simplifying:

Hence, (A) is correct.
-
B
Difficulty: Hard
Getting to the Answer: The question presents a variation of a quadratic equation. A glance at the radicals in the answer choices suggests that using the quadratic formula to solve is appropriate. Because there are so many variables, it might help to write down the quadratic formula in your notes as a guide
 .
. Begin by reorganizing the quadratic into the standard form ax2 + bx + c = 0:

In this case, a = 3, b = −5m, and c = −mv. Now solve:

Therefore, (B) is correct.
Page 354 -
D
Difficulty: Medium
Getting to the Answer: Get the equation x(dx + 10) = −3 into the form ax2 + bx + c = 0. Multiply out the left side of the equation x(dx + 10) = −3 to get dx2 + 10x = −3. Add 3 to both sides to yield dx2 + 10x + 3 = 0.
When a, b, and c are all real, the equation ax2 +bx + c = 0 (when a ≠ 0) does not have real solutions only if the discriminant, which is b2 − 4ac, is negative. In the equation dx2 + 10x + 3 = 0, a = d, b = 10, and c = 3. The discriminant in this question is 102 − 4(d)(3) = 100 − 12d.
Since you’re looking for a negative discriminant, that is, b2 – 4ac < 0, you need 100 – 12d < 0. Solve the inequality 100 – 12d < 0 for d:

Among the answer choices, only 10 is greater than
 , so (D) is correct.
, so (D) is correct. -
C
Difficulty: Medium
Getting to the Answer: Recall that when a quadratic equation has no real solutions, its discriminant, which is b² − 4ac, will be less than 0. Calculate the discriminant of each answer choice and pick the one that’s negative. You don’t need to actually solve for x:
(A) 8² − 4(1)(−12) = 64 + 48 > 0. Eliminate.
(B) (−8)² − 4(1)(12) = 64 − 48 > 0. Eliminate.
(C) (−9)² − 4(1)(21) = 81 − 84 = −3 < 0. Pick (C) and move on. For the record:
(D) (100)² − 4(1)(−1) = 10,000 + 4 > 0. Eliminate.
-
B
Difficulty: Easy
Getting to the Answer: Quadratic equations can be written in several different forms that tell various pieces of important information about the equation. For example, the constant k in the vertex form of a quadratic equation, y = a(x − h)2 + k, gives the minimum or maximum value of the function. The standard form, y = ax2 + bx + c, gives the y-intercept as c. The factored form of a quadratic equation makes it easy to find the solutions to the equation, which graphically represent the x-intercepts. Choice (B) is the only equation written in factored form and therefore is correct. You can set each factor equal to 0 and quickly solve to find that the x-intercepts of the graph are
 and x = 1, which agree with the graph.
and x = 1, which agree with the graph. -
C
Difficulty: Medium
Getting to the Answer: An axis of symmetry splits a parabola in half and travels through the vertex. Use the formula to find h, plug in the correct values from the equation, and simplify:
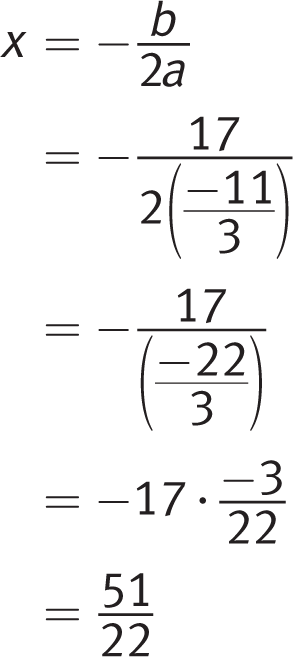
The correct answer is (C).
Page 355 -
B
Difficulty: Hard
Getting to the Answer: To find where the two functions intersect, set them equal to each other and solve for x:

Notice that this is a classic quadratic:

Since there is only one solution for x, there must be only one point of intersection. (B) is correct.
-
2
Difficulty: Medium
Getting to the Answer: An x-intercept of a function is a point at which the y-coordinate equals 0. Set the equation equal to zero, simplify, and factor:

The question asks for the difference between the x-intercepts, not for the x-intercepts themselves. Thus, 3 − 1 = 2.
-
A
Difficulty: Hard
Getting to the Answer: The answer choices are all similar, so pay special attention to their differences and see if you can eliminate any choices logically. A rocket goes up and then comes down, which means that the graph will be a parabola opening downward. The equation, therefore, should have a negative sign in front. Eliminate (C) and (D).
To evaluate the two remaining choices, recall the vertex form of a quadratic, y = a(x − h)2 + k, and what it tells you: the vertex of the graph is (h, k). The h is the x-coordinate of the maximum (or minimum) and k is the y-coordinate of the maximum (or minimum). In this situation, x has been replaced by t, or time, and y is now h(t), or height. The question says that the maximum height occurs at 3 seconds and is 34 feet, so h is 3 and k is 34. Substitute these values into vertex form to find that the correct equation is y = −16(x − 3)2 + 34. The function that matches is (A).
-
B
Difficulty: Medium
Strategic Advice: Because each of the two expressions containing b is equal to a, the two expressions must be equal to each other.
Getting to the Answer: Set the two expressions equal to each other, and then solve for b:
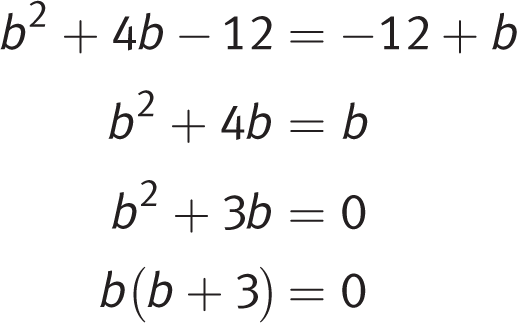
If
 , then b = 0 or b = −3. Of these two values, only −3 is among the answer choices, so (B) is correct.
, then b = 0 or b = −3. Of these two values, only −3 is among the answer choices, so (B) is correct. -
2
Difficulty: Medium
Getting to the Answer: The points of intersection of the graphs are the points at which the equations are equal. Since (a, b) is the label for an (x, y) point, set the two equations equal to each other and solve for the value of x to find the value of a:

Thus, x = 0 or x = 2. The question states that the intersection points are (0, 0) and (a, b), so a must equal 2. Grid in 2.Page 356
-
B
Difficulty: Medium
Getting to the Answer: The solutions to a system of equations are the points at which the equations intersect, which occurs when they are equal. Begin by setting both equations equal to y:
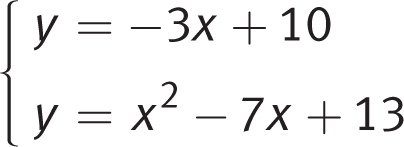
Because both equations are equal to y, they are also equal to each other. Set them equal and solve for x:

Thus, there are 2 solutions, x = 1 and x = 3. (B) is correct.
Note that you could also use the discriminant,
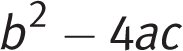 , to determine how many solutions there are. If the discriminant is greater than 0, there are two real solutions; if it’s equal to 0, there is one real solution; and if it’s less than 0, there are no real solutions. In this case,
, to determine how many solutions there are. If the discriminant is greater than 0, there are two real solutions; if it’s equal to 0, there is one real solution; and if it’s less than 0, there are no real solutions. In this case,  . Because 4 > 0, there are 2 real solutions. (B) is correct.
. Because 4 > 0, there are 2 real solutions. (B) is correct. -
C
Difficulty: Hard
Getting to the Answer: Because the question states that f(c) = g(c), set the two functions equal to each other and solve for x. To make calculations easier, begin by converting f(x) into standard form:

Now set the two functions equal:

Simplify by dividing all terms by −2:

Next, combine like terms and solve for x:

Therefore, x = 2 or x = 3, which means that c could also be either 2 or 3. Because 3 is not an answer choice, the answer must be 2. (C) is correct.
-
C
Difficulty: Hard
Strategic Advice: When you need to find the points of intersection of two equations, set the equations equal to each other.
Getting to the Answer: The question indicates that points P and Q are the points of intersection of the two equations, so set the two equations equal to each other, consolidate terms to get a single quadratic equation equal to 0, and simplify:

Factor the equation to find the values of x:

You can plug each value of x into either of the original equations to find the corresponding values of y. (The linear equation appears easier to work with.) For x = −4:

Page 357Therefore, one of the points of intersection is (−4, 5). Find the other point of intersection by plugging in 2 for x into the linear equation:

Thus, the other point of intersection is (2, −3).
The question asks for the distance between these two points. The formula for the distance, d, between the points (x1, y1) and (x2, y2) is
 . Thus, find the distance between points P and Q:
. Thus, find the distance between points P and Q: 
Therefore, the distance between points P and Q is 10. (C) is correct.
-
C
Difficulty: Medium
Getting to the Answer: The first approach is to set f(x) equal to g(x): 4x2 − 25 = −4x2 + 25. Isolate the x2 terms on one side to get 8x2 = 50, so 4x2 = 25. Take the square root of both sides to see that 2x = ±5, which means that the two intersections of the functions occur where x = −2.5 and x = 2.5. From the graph, you can see that these are the values of ±z, so z = 2.5. (C) is correct. (Note that even if you had not been given the y-coordinates of the points of intersection, you could have calculated them from knowing their corresponding x-coordinates.)
The second approach is to plug in the coordinates of one of the intersections into either function. Using f(x), the y-coordinate is 0 and the x-coordinate is z. So, 0 = 4z2 − 25. The math works out exactly the same as the first method: 4z2 = 25, so z = ±2.5, and, from the graph, you can determine that z = 2.5.
-
40
Difficulty: Medium
Category: Graphs of Quadratics
Getting to the Answer: Since the given equation is valid for both x = −5 or x = 7, you can plug in either of those values and solve for k. Using 7 as the value of x gives you
 . Multiply both sides by 4 to get 4(49) − 56 − k = 120. Thus, −k = 120 − 196 + 56 = −20, so k = 20 and 2k = 40. Grid in 40.
. Multiply both sides by 4 to get 4(49) − 56 − k = 120. Thus, −k = 120 − 196 + 56 = −20, so k = 20 and 2k = 40. Grid in 40. -
D
Difficulty: Hard
Category: Graphs of Quadratics
Getting to the Answer: Because the quadratic regression is an exact fit of the data, you can treat the data points as a quadratic function.
The graph of a quadratic function is symmetric with respect to its axis of symmetry, which passes through the x-value of the vertex, or the maximum (or minimum) of the function. The question tells you the maximum occurs at x = 25, which makes it the line of symmetry. Because 35 is 35 − 25 = 10 units to the right of the axis of symmetry, you know that the y-value will be the same as the point that is 10 units to the left of the axis of symmetry, which is x = 25 − 10 = 15. Find the corresponding y-value in the table: 27. Therefore, (D) is correct.
-
C
Difficulty: Hard
Category: Graphs of Quadratics
Getting to the Answer: Because the height of the boulder is expressed as a quadratic equation with a negative t2 coefficient, the path of the boulder is a downward-facing parabola. Therefore, the maximum height occurs at the vertex of the parabola. The t‑coordinate (generally called the x-coordinate) of the vertex of a parabola is given by
 . Plug the result into the function to get the h‑coordinate: h (7) = −16(7)2 + 224(7) + 240 = 1,024. (C) is correct.Page 358
. Plug the result into the function to get the h‑coordinate: h (7) = −16(7)2 + 224(7) + 240 = 1,024. (C) is correct.Page 358 -
D
Difficulty: Medium
Category: Graphs of Quadratics
Getting to the Answer: Set the quadratic expression for the height of the boulder equal to 0 and solve for t:

Because time can’t be negative, t = 15. (D) is correct.
-
B
Difficulty: Medium
Category: Graphs of Quadratics
Getting to the Answer: Keep in mind that the question asks for the statement that’s false, so eliminate the true choices as you go. The parabola opens downward, so the a term should be negative. Eliminate (A). The parabola’s vertex is in quadrant I, so h and k are both positive. That makes choice (D) true as well; eliminate it. The axis of symmetry is x = h, so x = 3. According to the graph, the vertex is (3, 2). Choice (B), however, claims that the axis of symmetry is y = 3. Choice (B) is false and is therefore the correct answer.
For the record, (C) is a true statement because the line
 passes through the point (3, 2), which is indeed the vertex of f(x).
passes through the point (3, 2), which is indeed the vertex of f(x). -
24
Difficulty: Medium
Category: Systems of Quadratic and Linear Equations
Getting to the Answer: The question tells you that y = 2x, so solving the system using substitution is a good option. Divide the second equation by 2 and plug in 2x for y:
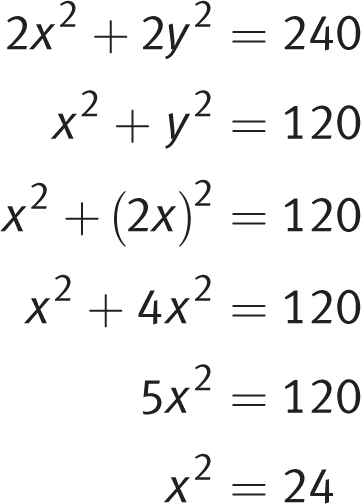
The question asks for the value of x 2, not x, so stop here. Grid in 24.
-
D
Difficulty: Medium
Category: Completing the Square
Getting to the Answer: The x-intercepts of a function are the values of x that make the function equal to 0. Factoring this function would be cumbersome because you would need to determine two numbers whose product is
 and whose sum is −7. This is a good candidate for completing the square.
and whose sum is −7. This is a good candidate for completing the square.Start with
Page 359 , then subtract
, then subtract  from each side to get
from each side to get  . Half of the b coefficient, −7, is
. Half of the b coefficient, −7, is  , which, when squared, is
, which, when squared, is  . Add that to both sides to get
. Add that to both sides to get  . So
. So  . Take the square root of both sides to get
. Take the square root of both sides to get  . Therefore, the x-intercepts are
. Therefore, the x-intercepts are  , or
, or  and
and  . (D) is correct.
. (D) is correct. -
D
Difficulty: Medium
Category: Graphs of Quadratics
Getting to the Answer: Draw a quick sketch of the equation (or graph it in your graphing calculator):
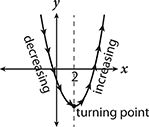
Based on the equation, the graph is a parabola that opens upward with a vertex of (2, −5). A parabola changes direction at the x-coordinate of its vertex. You can immediately eliminate (A) and (B). To the left of 2 on the x-axis (or x < 2), the parabola is decreasing, and to the right of 2 on the x-axis (or x > 2), it is increasing. (D) is correct.
-
A
Difficulty: Medium
Category: Solving Quadratics by Factoring
Getting to the Answer: Rearrange the given equation to read (6x + 5)2 = (3x − 2)2 . Given that the square of a number is the same value as the square of its negative counterpart, you can write that ±(6x + 5) = ±(3x − 2). Therefore, either 6x + 5 = 3x − 2 or 6x + 5 = (−1)(3x − 2) = −3x + 2.
Solve the first case by subtracting 3x and 5 from both sides of the equation: 6x + 5 − 3x − 5 = 3x − 2 − 3x − 5. Thus, 3x = −7 and
 . For the alternative equation, add 3x to and subtract 5 from both sides: 6x + 5 + 3x − 5 = −3x + 2 + 3x − 5. Thus, 9x = −3, so
. For the alternative equation, add 3x to and subtract 5 from both sides: 6x + 5 + 3x − 5 = −3x + 2 + 3x − 5. Thus, 9x = −3, so  .
.The question asks for the sum of the two solutions which is
 . (A) is correct.
. (A) is correct. -
A
Difficulty: Hard
Category: Classic Quadratics
Strategic Advice: Technically, this isn’t a quadratic equation because the highest power on the variable isn’t 2. However, it is a “quadratic-type” equation because the square of the variable part of the middle term is equal to the variable in the leading term. In other words, squaring
 gives you x. You can use factoring techniques you learned for quadratics to answer the question.
gives you x. You can use factoring techniques you learned for quadratics to answer the question.Getting to the Answer: The presence of 4, 9, and 16—all perfect squares—is a big clue. Note that
 is an instance of the classic quadratic (a − b)2 = a2 − 2ab + b2. Use this shortcut to factor the equation and see where that leads you:
is an instance of the classic quadratic (a − b)2 = a2 − 2ab + b2. Use this shortcut to factor the equation and see where that leads you:
The question asks for
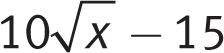 , which happens to be 5 times the quantity on the left side of the last equation above, so multiply the positive result, 4, by 5 to get 20. The correct answer is (A).
, which happens to be 5 times the quantity on the left side of the last equation above, so multiply the positive result, 4, by 5 to get 20. The correct answer is (A). -
A
Difficulty: Medium
Category: Solving Quadratics by Factoring
Strategic Advice: When a question asks for a value of an expression, isolate that expression on one side of the equation, if possible, rather than solving for the variable.
Getting to the Answer: Notice that the question asks for a possible value of x − 2, not x. Isolate x − 2 on one side of the equation by multiplying both sides by x − 2 and taking the square root of both sides:

Thus, (A) is correct.
An alternative strategy is to backsolve, plugging each choice in for x − 2 to see which results in a true statement. Page 360
-
A
Difficulty: Hard
Category: Classic Quadratics
Getting to the Answer: Use exponent rules to simplify the fraction. Since the terms in the numerator and denominator have the same base, z, subtract the exponent of the denominator from that of the numerator:
 . When a value with an exponent is raised to another exponent, multiply the exponents. So, for the term on the right side,
. When a value with an exponent is raised to another exponent, multiply the exponents. So, for the term on the right side,  . Now the equation is
. Now the equation is  . Since both sides have the common base, z, their exponents must be equal and you can write
. Since both sides have the common base, z, their exponents must be equal and you can write  .
.Factor
 , a classic quadratic, to get
, a classic quadratic, to get  . Thus, x + y must be either 3 or −3. However, the question limits x and y to positive integers, so they must be 1 and 2. Furthermore, since x > y, x must be 2 and y must be 1. Consequently, x − y = 2 − 1 = 1. (A) is correct.
. Thus, x + y must be either 3 or −3. However, the question limits x and y to positive integers, so they must be 1 and 2. Furthermore, since x > y, x must be 2 and y must be 1. Consequently, x − y = 2 − 1 = 1. (A) is correct.