In this chapter we examine the notion of “active learning” through Wilber’s Integral AQAL Model and through two learning models based on AQAL. Our examination of Edwards’ integral learning and Renert and Davis’ five stages of mathematics, results in a multi-perspective, multi-level notion of “active learning”. We demonstrate, through the development of a rubric to gauge students’ “activeness”, the complexity of what is involved in the teaching and learning process when one becomes mindful of the perspectives and levels (AQAL) that are present for every student. Several episodes of learning are used to show how each theoretical model applies, and an extended episode, which illustrates a student’s repair strategy on a mathematically erroneous concept, is used to illustrate the analysis of the extent of active learning. The chapter concludes with a discussion of how the rubric of active learning, along with the four continua, can help teachers be mindful of the multiple perspectives that influence learning.
In Sir Francis Bacon’s (1597) Meditationes Sacrae, “ipsa scientia potestas est” translates to “knowledge itself is power.” Sir Bacon had the insight that the quest for knowledge give learners power throughout the learning process to take control and make use of their ideas. Sadly, such instances of taking control are few and far between for modern day school mathematics learners, who are bogged down by state standards and arguably excessive standardized testing. This book chapter argues and advocates a respectful space in the learning environment so that active pursuit in mathematics learning can indeed empower the learner to sustain future active learning. Based on the mindful experience of one of the authors, we will examine the meaning of active learning through a fourfold learning dynamic, corresponding to the four quadrants in the Wilber’s Integral Model, which will be elaborated on in Figure 1.
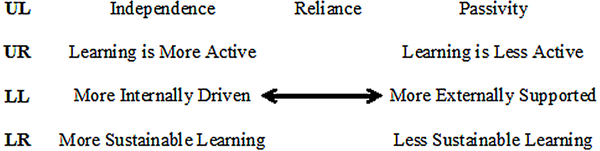
| Figure 1. A rubric of four continua in the UL, UR, LL, and LR quadrants describing active learning within the framework of Wilber’s Integral Model |
|---|
 |
To examine these notions we will use three established models: Renert and Davis (2010) five stages of mathematics, Edwards’ (2005) integral learning, and Wilber’s All Quadrant All Level (AQAL) Integral Model. The three models are used to explain: “What constitutes mathematics?”, “How can mathematics be learned?”, and “How can learning dynamics be thoroughly and integrally examined?” The examples and illustration of mathematics learning are all drawn from the experience of one college level developmental mathematics and calculus teacher. The students described in this chapter include both the traditional college learners who attended college immediately after high school graduation, as well as the non-traditional college learners who returned to college after a hiatus from formal education since their high school graduation. The results of the examination will have both empirical and theoretical implications. The research account of the author Yuen, a college math instructor, who attempted to engage his students in a genuine learning process, is based on his mindful observations and reflections of what was happening in his classroom. We describe Yuen’s observations first in the context of his individual classroom, and subsequently we discuss how to be mindful of a student’s learning space as well as the social learning environment, in order to foster active learning in a mathematics classroom.
PROBLEM AND CONTEXT: LEARNING SCHOOL MATHEMATICS
In the context of classroom mathematics instruction, a sociologist might ask why the subject of mathematics seems to have an overall reputation of being stubborn to learn. A psychologist might ask why individual learners suffer from mathematics anxiety. An educator might ask how to best facilitate mathematics instruction. And for individual learners, what should they ask about their mathematics learning? Most ask, “Is that the right answer?” The author Yuen has been teaching mathematics professionally for 15 years, during which time not one single student has ever posed the questions: “What does it mean to do math?” or, “What is math?” Suppose a learner does know what it means to do mathematics, then this knowledge could serve as a prerequisite for active learning. In other words, there is a possibility for active learning to take place when the learner knows what he/she is doing. However, it is unclear whether many mathematics learners do have a clear idea what mathematics means. Does using a formula mean doing mathematics? Does solving an equation mean doing mathematics? How does an educator constructively instill in learners and empower them with the prerequisite of what mathematics could mean to them and to the academic community as a whole?
An Episode of an Adult Learning the Notion of “Perimeter”
As an illustration, we will describe an episode of learning that happened recently in a developmental math classroom. The lesson was showing how to find perimeters of polygons--perimeter being the length of the path that completely wraps around a two-dimensional polygon. For many adult learners, this topic was mostly a review, but perhaps it was worthwhile to spark meaningful discussion and reasoning among them. Indeed, some learners pointed out that in a rectangle with two lengths and two widths, one could add the lengths of all four sides, but may be more efficient. Another student chimed in with her thought that
might work also because if one knows the sum of the length and width, then one could double the sum to find the perimeter. All in all, reflecting on teaching, the classroom discussion was productive, and so the teacher began to assign a group classwork. To the teacher’s surprise, when one student attempted the perimeter of a triangle in the worksheet, she argued with her fellow group mates to add the measurements of each of the three sides, and insisted that they then must multiply that sum by two because the teacher said so. While the student was quickly corrected by her group mates, it was, nevertheless, an interesting encounter because her ill-formed reasoning made the instructor reflect on the teaching. Was she doing (or developing) math? Did she believe that she was doing math? Was she actively learning? Many might argue that she was actively learning because she was en route to developing geometric reasoning. After all, she was engaged in the concept of perimeter, and she was developing argumentation skills as well as geometric reasoning skills. Most math teachers would consider this vignette a productive and satisfying experience. However, what this student left the instructor pondering about was where she had acquired the skills to so passively follow the same reasoning for calculating the perimeter of a rectangle. We would argue that there is room yet for further active learning.
In a recent study, Givvin, Stigler, and Thompson (2011) developed a hypothetical account of how the school environment plays a role in the behaviors of adult learners of college mathematics. Coupled with past research from Wieschenberg (1994) and De Corte, Verschaffel, and Depaepe (2008), which claims that learners often do not make sense of content materials (a.k.a. sense abandonment), this makes the subject of math particularly challenging to actively engage learners in a meaningful way. As a matter of fact, one could argue in the above vignette that the learner did abandon sense-making by doubling the sum of the three sides of a triangle. In this context, how should a classroom instructor effectively engage learners in the math discourse in an active manner? While active learning has been defined as “any instructional method that engages students in the learning process” (Bonwell & Eison, 1991; Prince, 2004), the definition provides a broad space for interpretation: What constitutes engagement? Who conducts active engagement? The instructor, the learner, or both? Who maintains control of the learning activities? How is control sustained? And at what level of development should active learning take place? In fact, through the above vignette, one could argue that active learning took place, but perhaps one should advocate for a larger extent of active learning.
A Mindful Mathematics Teacher
Careful observations of learning, in all its modes, as it happens minute by minute in the classroom, require a degree of mindfulness on the part of the teacher. In popular culture and media, “mindfulness” is often referred to as “paying attention”, “being present in each moment”, and “the opposite of multitasking.” A more accurate description of mindfulness would involve the component of ‘non-attachment’ to one’s observations, which is an activity closely related to phenomenological “bracketing”. In the introduction to The View from Within, Francisco Varela (1999) described this process of careful observation, without the observer becoming personally and emotionally involved with the observations and ideas themselves, in his comparison of Husserl’s phenomenology and the mindfulness meditation process.
Most people who have grown up in the western culture experience considerable difficulty in their initial attempts at mindfulness training. The idea of sitting quietly and placing one’s full attention on one thing – for example one’s breath – seems simple enough, for about 5 seconds, at which point the novice meditator generally becomes distracted by mental chatter. The untrained mind tends to be constantly multitasking, unconsciously jumping from thought to thought. Given this perpetually distracted state, it is not difficult to imagine how much valuable information and insights could be missed by a teacher during the course of a lesson. For a teacher who intends to engage students in authentic, active learning, mindfulness is an essential skill.
Deep Learning and Surface Learning
To clarify the discussion to follow, we will make the distinction between deep learning, which associates with conceptual knowledge, as opposed to surface learning, which associates with procedural knowledge. Willingham, Nissen, and Bullemer (1989) described procedural knowledge as “the acquisition and retention of skilled performance … indexed by tasks in which memory is expressed implicitly by changes in performance as a result of prior experience” (p. 1047). Note that the description explicitly appeals to tasks, memory, and prior experience. In traditional math learning, learners are often subjected to practices and drills where one practices a procedure over and over again. This kind of exercise falls within the acquisition of procedural knowledge. For example, Schoenfeld (1989) reported that “[s]tudents were expected to master the subject matter, by memorization, in bite-size bits and pieces” (p. 344), and his observation clearly suggests that a great deal of math learning involves the acquisition of procedural knowledge. Contrary to procedural knowledge that relies on tasks, memory, and prior experience, conceptual knowledge appeals to reasoning and generalization. Star (2005) asserts that “conceptual knowledge has come to encompass not only what is known (knowledge of concepts) but also one way that concepts can be known (e.g. deeply and with rich connections)” (p. 408). Furthermore, he concluded that “[conceptual knowledge] is defined in terms of the quality of one's knowledge of concepts—particularly the richness of the connections inherent in such knowledge” (p. 407). For a learner to develop the connections inherent in knowledge, he/she must be given due learning and cognitive space for one to allow attempts at such connections. While Star argued that there is an emphasis of conceptual knowledge over procedure knowledge, the two are indeed richly interconnected, and Edwards’ (2005) idea of integral learning, adapted from Wilber’s Integral Model, as a theoretical framework may be able to link the two in a balanced manner.
CONSIDERING THREE THEORETICAL MODELS
According to Denscombe (2010), action research as a method aims to solve a practical problem and to produce guidelines for best practice. (Table 0.1 on p. 6). In the previous section, the problem was outlined, and it was unclear whether a learner genuinely does mathematics or merely follows procedures. To this end, one could argue that merely following procedures is a form of learning with a certain degree of passivity. A worthwhile goal for mathematics teachers is to facilitate the students away from this passive way of learning. In essence, mathematics instruction should ideally aim learners toward engaging in creative problem solving activities, thus fostering an environment for the learners to solidify their notion of what doing mathematics means to them. When a learner is able to independently undertake solving a mathematical problem using his/her repertoire of skills and logical reasoning, then it can be argued that there is a degree of active involvement between the learner and the posed problem. In other words, active learning is achieved. In this sense, action research as a method, coupled with reflecting on observations from this instructor’s teaching experience, is appropriate for the inquiry of this particular problem. The theoretical framework for this article involves three models:
Model 1: Five Stages of Mathematics
To better understand the problem, one ought to ponder what mathematics entails. The first model addresses the notion of what mathematics is. Davis (1996) and subsequently Renert and Davis (2010) have proposed math as five stages or mentalities: oral, pre-formalist, formalist, hyper-formalist, and post-formalist (Renert & Davis, 2010, pp. 180–183). A brief description of each stage follows:
While the five mentalities of mathematics provide a wide spectrum of what entails math, the math education practice generally sees subject content as an inert, unchanging body of knowledge, mainly as pre-formalist and formalist mathematics. This is possibly because U.S. school mathematics curricula has been highly standardized, mainly by the National Council of Teachers of Mathematics’ (NCTM) Principles and Standards, as it has been regulated, such as with the 2001 U.S. Act of Congress on No Child Left Behind Act (NCLB). Ernest (1985) has made a similar observation that: “[i]n educational terms this corresponds with the view of mathematics as an inert body of knowledge which instruction transmits to the student” (p. 607). Evidence of this view is abundant. Many parents experience their children’s mathematics materials as “new math,” as opposed to the “old math” of their own early education. They find it challenging to support their children’s education because they are unable to comprehend that “old math” and “new math” are different only in presentation and/or argumentation (Remillard & Jackson, 2006; Ginsburg, Rashid, & English-Clarke, 2008). Such ethnographic observations are examples of seeing math knowledge as an inert, unchanging body.
The claim of mathematical knowledge as an inert body is an important one, because many learners rely on an inert body to play a passive role in developing math knowledge, both inside and outside of classroom. A possible argument for this behavior is that the math education practitioners often play a passive role as recipients of mandated curriculum and standards, with a relatively small space in the educational discourse for them to actively engage themselves in co-creating curriculum for the general population. In turn, this relatively small space funnels to learners to engage themselves in experimentation or “play”. Such a lack of space has been reported; in fact, D’Amour (2013) wrote about the space intended for sense-making in the learning environment. The social dynamic, while well intended for learning to take place, may covertly discourage many learners to sustain “serious play” (p. 444) in learning. Instead, some learners may very well opt for “pretending” to play (p. 442) in the learning environment. In other words, D’Amour argued that the learner’s internal process at play has not sufficiently been respected, and mathematics teachers do not recognize this internal process because they generally are unaware of its existence or importance. Such a failure of recognition leads to a social dynamic that is not conducive to the intended authentic learning, but rather perhaps is conducive to raising anxiety among mathematics learners.
Model 2: Edwards’ Integral Learning
Now that we have set a basis for what it means to do mathematics, we could turn the focus to what it means to learn mathematics. For the simplicity of discussion, we will table Wilber’s Integral Model until after the discussion of integral idea. Edwards (2005) adapted from Wilber’s model and proposed Edwards’ integral learning, outlined as below:
After the strand (4), an active learner would begin observing and collecting data again, bringing the illuminative strand into full circle. This also makes (1) to (2) to (3) to (4), and then back to (1) a cyclic learning process.
One can illustrate the four strands in an example of learning differentiation in calculus. In the first calculus meeting, an instructor shows a position function and a velocity function of an object, and students are asked to determine the connectedness between the two curves1. What the students would find out in an activity like this is “what is happening?” through observations of the two functions. This would be the illuminative strand. Traditionally, the instructor would introduce differentiation through its definition:
The definition involves abstraction of the visual function curves and the symbolism to capture the connectedness of the functions. This is the interpretative strand of learning where cultural meaning of the definition of differentiation would be co-created. Once this strand completes, learners may be moving on practicing differentiation using the developed definition. The interaction between the instructor, where the instructor serves as an outsider (in Wilber’s terminology, “exterior”) and learner who provide formative feedback on learners’ work would be learning in the validative strand in which the learners continue to refine the concept of differentiation. Finally, when a learner departs from the calculus class, and goes to a different class, say physics, when he/she may be working on a physics concept involving differentiation, such as velocity and acceleration of objects, then the learner can readily apply what has been developed in calculus to physics as a separate field. This would describe the learning in the injunctive strand. After experiencing learning and applications outside of the mathematics course, the learner may reflect, compare the ideas and concepts in different context, and doing so would likely create newfound meanings that the original learning of differentiation did not uncover. Then, the learner is engaging in the illuminative strand of learning. This completes the four strands in a cycle. Ideally, the cycle can repeat itself to develop deeper knowledge and probe further into conceptual nature.
Edwards’ integral learning has multiple relations with the Renert and Davis’ five stages of mathematics. The oral and pre-formal stages often relate to the illuminative strand of experiential learning. The development of “What is happening?” is often conducted through some mental pondering, and through informal writing/diagraming. An active learner would strive to make sense through organizing thoughts and reorganizing ideas, in multiple trials if needed, in order to make initial sense of the mathematical concept that is of interest. This kind of active learner could be nurtured through a past history of respected learning space, in which they are allowed to freely “play” (See D’Amour, 2013) with mathematical concepts. In the second, interpretative strand that Edwards proposed, the natural question becomes “What does it mean?” The learning in this strand brings concrete ideas into something abstract and conceptual. This strand relates to the pre-formal and formal stages where instructors often play a role in facilitating learners to develop pre-formal math ideas into formal language, notation, and proofs. Often, an active learner develops meaningful interplay between his/her ideas and thoughts and connects them to their corresponding formalism, while a relatively passive learner may cease to construct meaning, and see his/her own math ideas and their corresponding formalism as two unrelated objects. Some passive learners may even abandon making sense of formalism as the abstraction is seemingly too challenging to comprehend. A skilled instructor generally finds ways to encourage passive learners to become more active in this strand. A further discussion of this strand will be discussed in the section of Wilber’s Integral Model.
The validative strand in Edwards’ model begs the question of “What have we learned?” where a learner has to summarize and communicate what mathematical concepts have been developed. This is also the strand where the learning would be assessed in a sense that learning is judged as a 3rd party object. Has the social learning environment been effective in reaching the learning objectives initially set forth? Can other people outside of the classroom comprehend and make sense of the math discourse developed in the learning environment? If so, to what extent? This strand corresponds to the pre-formal and formal stages of mathematics, as those are the tools to engage in math discourse. Characteristics of an active learner in this strand would show competence is using formalism engaging mathematics discourse, contrasting with a passive learner who may be indecisive toward the use of mathematical symbolism in decisions made based on mathematical properties and/or logic, or both of the above. The fourth, injunctive strand of learning correlates to outside application after a learner has developed a mathematical concept to its maturity. Some active learners may use the developed concepts in science, technology, and engineering, and a few others may choose to pursue higher mathematics. For those who choose to pursue higher mathematics, those active learners are more likely to engage in the hyper-formal stage of mathematics, developing mathematical ideas for mathematics sakes. Some may even engage in learning by developing ideas in the post-formalist stage, most likely through graduate training.
The notion of “active learning” through Edwards’ integral learning can be seen as microscopic in each strand of learning, as well as in the cyclic nature of the four strands:
Model 3: Wilber’s AQAL Integral Model
The third model for discussion addresses how one observes learning as a phenomenon. The basic five recurring elements of Wilber’s Integral Model, often known as AQAL, are: quadrants, levels, lines, states, and types. Sean Esbjorn-Hargens (2006b, 2009, 2011) has devoted many years to making Wilber’s Integral Model accessible to researchers and practitioners. The model itself has been continually elaborated upon and refined by Wilber from its initial form in Spectrum of Consciousness (1993) to the present form, with Integral Spirituality (2006) being particularly helpful in outlining the nuances of the model clearly.
All Quadrants
Esbjörn-Hargens (2006a) described the quadrants as the “basic perspectives an individual can take on reality” (p. 5). This includes the interiors and exteriors of the individuals and the collectives, and each permutation, called a “quadrant,” is irreducible, with its own valid claim and its own mode of investigation. The following figure illustrates the characteristics of the four quadrants as a fourfold, co-arising lens (see Table 1).
Table 1. An illustration of the characteristics of the quadrants in AQAL
| Interior | Exterior | |
|---|---|---|
| Individual | Upper Left (UL) Interior-Individual, subjective: • The “I”: 1st person perspective on experience, introspection (e.g., phenomenology) • Emotions, beliefs, feelings • Self-reflection on the “I” consciousness |
Upper Right (UR) Exterior-Individual, objective: • The “It” 3rd person perspective • How it – individual organism -functions (e.g., cognitive science) • How it behaves, how it learns • Empirical observations |
| Collective | Lower Left (LL) Interior-Collective, intersubjective: • 1st and 2nd person perspectives – how do you and I understand each other (e.g., hermeneutics) • 1st person plural – we- Cultural • How do we function as a collective |
Lower Right (LR) Exterior-Collective, interobjective: • The “They” 3rd person perspectives – how do groups organize and interact within systems - Social • The “Its” 3rd person perspectives – patterns of interactions of systems |
The All Quadrants approach examines a psychosocial phenomenon through four different perspectives:
The inquiry into MALP could reveal its nature in great detail through the four perspectives (A.K.A. the quadrivium) because “[t]he quadrants provide a particularly helpful lens for researchers in that the left-hand and right-hand quadrants are associated with qualitative and quantitative methods respectively” (Esbjörn-Hargens, 2006b, p. 84). Essentially, this means that the All Quadrants approach is a mixed-method approach. As a means to pursue the meaning of active learning, recall the previous Figure 1.
The UL quadrant corresponds to the individual learner’s learning mode from the first-person perspective. As such, one might describe whether one is an independent learner on one end of the continuum. On the other end, one might characterize oneself as passive. While learning may not be completely independent within the current learner population in discussion, it is important to point out that the balance of the two ends, where a learner characterizes oneself as reliant, would be a position poised for becoming independent.
The UR quadrant corresponds to third person observations, usually from the teacher, formatively describing the quality of learning of an individual learner, whether the learning is considered relatively active or relatively inactive. In an ideal situation, the learner’s UL perspective and the teacher’s UR perspective should reach congruence in order to foster a healthy learning environment. A disagreement of between the two perspectives can often happen quite frequently in a mathematics classroom where what an individual believes he/she is learning may not be what a teacher attempts to develop. For a hypothetical example, a student might assert, “I don’t understand why the professor has to do all these proofs in class, I just need to learn to integrate so that I can do well on the next midterm.” Here, the student may believe he/she is actively pursuing a realistic goal in learning the procedure of integrating functions in a calculus course, but the professor might attempt to instill literacy and fluency the underlying numerical, graphical, and algebraic connections that could be united by some form of calculus. Under Renert and Davis’ five stages, it seems that this story exemplifies the professor targeting at the formalist stage, but the learner might not agree to the importance and its deliberation of the stage.
The LL quadrant corresponds to the culture of the learning environment (first person plural – we) and the intersubjective aspect of learning (first and second person singular). A group of learners who are actively engaged can be construed as internally driven to reach learning goals, either overtly set as a group or tacitly agreed upon. A mindful teacher, as described in the previous section, could facilitate a group learning session by actively listening to the group’s discussion and occasionally offering constructive ideas, and the group would then be able to “run” with these ideas. This compares the group dynamic characterized as “more externally supported,” in which a group of students may not realize what learning goals are to be reached, wandering without a clear direction in their discussion. Facilitation from the teacher could often become a disconnected question and answer session where multiple questions sporadically reach different stages of mathematics, but they do not lead to an overall particular result to deepen learning in each individual. For example, once in a calculus course, a group of students were working on approximating the tangential slopes of various points of the curve . The goal of this exercise was to allow learners to visualize that differentiating
would yield the same function
. The group work divided the investigation among members. One learner did the calculation of the approximated tangential slopes of various chosen points; another learner tallied up the results in a table; and a third learner graphed the results for a visual representation. The investigation activity spanned across the numerical, tabular, and graphical aspects of the property of
, and this activity was used to develop conceptual understanding in the informal stage before a more formal algebraic proof of
developed. The group was basically was internally driven to run itself, and the instructor was merely the observer, allowing them to discover the results by themselves. This contrasts with another group in the same class, who could not manage the division of labor, arguing how many of the “various points” on the graph one must have, and which x values were to be used. In fact, that particular group disconnected the table and the graph, and the instructor had to intervene to redirect them until they could uncover the connectedness among the three aspects of the investigation. In sum, this group required tremendous external support, and the end result of the investigation may have had qualitative differences in reaching the end goal compared to the more internally driven counterpart.
The LR quadrant is a third person perspective of how active learning takes place for a collective of learners within a system (classroom –“they” and the college – “its”). They may be described as “sustainable” as they internally motivated each other during the learning process. On the other hand, a group that requires external support could be described as “less sustainable” because the group may require resources to clarify their ideas and discussion before the learning discourse can become coherent in reaching deep learning. In the above LL quadrant example of investigating , one observes the stark contrast between internally driven versus an externally supported group dynamics. Observations of the two dynamics from a third-person’s perspective can describe whether the dynamic is sustainable or not. Sustainability can be taken in all forms of interpretation, but one way to interpret it as a litmus test is whether or not the learning environment and the abilities possessed in the group of learners are sufficient to be transferable and generalizable to other learning goals and/or problem solving situations. In other words, in a different conceptual exploration, would either one of the above groups be successful in executing their investigation for developing new knowledge among them? The group that is observed with qualities to transfer their skills into developing new knowledge would be the one to be considered to have the capacity for sustainable learning.
Levels, Lines, States, and Types
Levels refer to the complexity of the psychosocial phenomenon in each of the basic quadrants. Esbjörn-Hargens (2009) made a distinction of the levels in different quadrants, referring them to as levels of depth and levels of complexity, and therefore, “[e]ach quadrant serves as a map of different terrains of reality” (p. 7). Renert (2011) described the notion as the “development through which phenomena in each quadrant have evolved and complexified …” (p. 17). Furthermore, he elaborated on “development” that it is “complex and nonlinear, with moments of progress and regress, stagnation and transcendence” (p. 17). Wilber has mapped out levels of human development, which increase in complexity as each includes and transcends the level from which it arises. These levels have been mapped out within each of the four quadrants. Initially, Wilber used terms primarily derived from psychology to describe each level (e.g., Wilber, 2000a), but subsequently has added colors and labels for greater accessibility in everyday use (e.g., Wilber, 2006). The colors progress from infrared to ultraviolet. Thus, the most frequently encountered levels in the classroom would be from Level 3 to Level 5:
Level 6 is the outer boundary of what Wilber refers to as First Tier development, where each level only affirms its own values. At present, Wilber estimates, using the many developmental theories and associated research which he integrated to define each level, (Wilber, 2000a) that the percentage of the general population operating at the Green level is small. Finally, Esbjörn-Hargens (2009) advocated the importance of levels because they represent many potential layers of development in each quadrant, and “practitioners [could] gain valuable traction by aiming their efforts at the appropriate scale [levels] and thereby finding the key leverage point” (p. 9).
Meanwhile, lines refer to the different paths of development within each quadrant. Esbjörn-Hargens (2006b; subsequently 2009) described the lines of development as the various distinct capacities that develop through levels in each aspect of reality as presented by the quadrants. In other words, the lines, which represent a person’s capacities or talents, also develop with increasing complexity and have their own developmental altitudes. As for states and types, his description was that states are “temporary occurrences of aspects of reality,” while types refer to the “variety of styles that aspects of reality assume in various domains” (p. 84). Further asserted, Esbjörn-Hargens (2006b) explained that integral theory “assigns no ontological and epistemological priority to any of these [five] elements” (p. 84) as they co-arise simultaneously, and “each of the five elements is understood to be part of each and every moment” (p.84).
AQAL and Mathematical Knowledge
The four quadrants are designed to disclose the reality of mathematical learning in a fourfold manner. Levels in the quadrants are important because they represent many potential layers of development in each quadrant, and “practitioners [could] gain valuable traction by aiming their efforts at the appropriate scale [levels] and thereby finding the key leverage point” (Esbjörn-Hargens, 2009, p. 9). In this case, Renert and Davis’ five stages of mathematical knowledge: oral, pre-formalist, formalist, hyper-formalist, and post-formalist, are encompassed in the levels:
USING INTEGRAL THEORY TO RE-ANALYZE THE LEARNING OF A STUDENT
Now that the models are presented in detail, we can re-analyze the previous example of the learner who erroneously applied the geometric argument of x2 to the triangle’s perimeter. Under the five stages of mathematics in Model 1, it seems that the learner attempted the use the step x2 holistically to the compute perimeters for all kinds of geometric figures. This indicates that the learner may not realize the effect of multiplying a value by 2, or the meaning of the formal notation x2. In other words, there seems to be a disconnect between pre-formalist and formalist stages of mathematics. Through informal discussion among group members, she quickly realized that x2 has an effect on the calculation that she did not intend, resulting in her learning of the oral and pre-formalist stages to bootstrapping her developed ideas and deepening mathematical concepts in a “how-to” manner. In terms of Wilber’s levels, her individual learning has transcended from Level 3 as pre-operational by treating x2 as a mysterious, nebulous step in the procedure to Level 4 as a concrete operation. This gives new (or rediscovered) meanings to multiplying a valued by 2 as an operation, and to applying this particular operation to create a certain effect. For example, one could potentially link x3 for the perimeter of an equilateral triangle, x4 for a square, and x5 for a regular pentagon, and so on. To reach Level 5 (and hyper-formalist), one could further the idea to a regular polygon of n sides, resulting xn as the operation to compute its perimeter.
As far as an analysis in Edwards’ model, this episode of learning encompasses three of the four strands, beginning with the illuminative strand, where the learner observed how perimeter was calculated and subjectively developed meaning in the details of the overall procedure. The learner also began to develop meaning to the concept of “perimeter” simultaneously in the illuminative strand. The disconnect that led to the error in applying x2 takes place in the interpretive strand where the subjective meanings from the illuminative strand did not successfully develop through the interpretative strand via an initial learning. However, through the social environment of group discussion, the learner re-interpreted x2 and deepened her mathematical knowledge to the formalist stage. The observation of the instructor, in this case, as to the effectiveness of the group discussion as well as individual learning was where the validative strand would take place. Presumably, the above example of hyperformalist stage of finding the perimeter of an n-side regular polygon by using xn could be used in this strand. This could validate how the procedure could be interpreted, verify the meaning of perimeter as well as deepen this particular mathematical knowledge among the learners, and formalize the reasoning and thinking process through more abstract mathematical objects. All of the work in the validative strand could lead to the injunctive strand as the learner may eventually apply the notion of perimeter and all the mathematics involved to her daily life and/or to a different field. Since the instructor could not observe this in the classroom, an account of this strand is not included in the analysis.
How Active Is Active Learning?
As far as active learning is concerned, this above detailed analysis illustrated how a mathematics teacher can develop mindfulness by examining active learning in a fourfold manner. We will use the rubric set forth for this chapter in Figure 1 to assess activeness in learning. In the UL quadrant, how reliant is a learner during the illuminative strand of learning? For the purpose of illustration, the measurement in each continuum is not exact, but is intended to give the reader an idea how a mindful teacher would be able to assess activeness during a student’s learning (Figure 2).
| Figure 2. |
|---|
 |
Continuing in the above analysis, the learner was independent enough to perceive the multiple steps in calculating perimeter, but she was relying the procedure to be stable (as opposed to flexible) so that ceasing to interpret the meaning of x2 would not affect the overall calculation and her mathematical performance. In other words, the learner’s level of development remained pre-operational. Because of reliance, the learner required external support among her group mates (Figure 3).
| Figure 3. |
|---|
 |
If she had been doing the classwork by herself, she would have practiced the erroneous procedure multiple times, while believing that she did well, and later find out how indeed what she did was incorrect, leading to frustration. However, being externally supported by her peers, she managed to deepen her understanding and mathematical reasoning. As far as the learning in the validative strand, one classifies that the group learning environment compensated for the individual learner’s reliance, so the group discussion indeed served the intended purpose (Figure 4).
| Figure 4. |
|---|
 |
In other words, instructors likely consider the group learning successful, and the group perhaps can sustain further independent learning to deepen mathematical knowledge. Finally, when evaluating the learning in the injunctive strand, then one could classify whether learning is indeed active or not (Figure 5).
| Figure 5. |
|---|
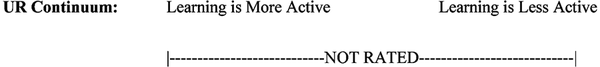 |
This episode does not show whether the individual learner applied the knowledge of perimeter into her personal life, in a different field, nor in a standardized test. Therefore, we do not evaluate the extent of activeness in the UR quadrant’s injunctive strand. Taken together, the four continua each represents a strand of learning, each exemplifies a perspective in a quadrant, and each resembles a parallelism to the various levels of development, revealing a nuanced and layered details in how active learning manifests in a complex manner in a mathematics classroom.
The above analysis provides some insight into the complexity of the phenomenon of teaching college mathematics, from one instructor’s perspective. We have included only a cursory reference to the instructor’s own world view at this point. From the current western conception of college mathematics teaching, which operates at Level 4 – Amber, conventional (Rule-Role-Mind) and Level 5 – Orange, postconventional (Systemic Mind) according to the general rhetoric of its policies and curricula, this is a fulsome analysis which provides the data that are relevant for the assessment of how mathematics is taught. The unit of analysis is the classroom, where an instructor employs a variety of teaching strategies and the students demonstrate their learning through their performance on the examinations. Student achievement then validates the teaching strategies. In this type of assessment, the context of the learning ends at the classroom door. The Integral Model suggests that a broader analysis should be subsequently employed, using Integral Methodological Pluralism (Wilber 2006, p. 35-39) along with Integral Epistemological Pluralism and Integral Ontological Pluralism, in order to more accurately locate the classroom in the many nested contexts with different and sometimes conflicting ontologies and goals. Every quadrant represents perspectives that can be investigated through corresponding methodologies (or methodological families), which in turn stem from epistemologies that are specific to each quadrant. Similarly, these epistemologies are related to quadrant specific ontologies. Thus, from a LR education system perspective, “math” is a proxy for a set of specifically defined skills, the attainment of which is determined by the student’s performance on the examination. The important required skill from this perspective is the skill of writing math exams. From the perspective of another system – the employment sector, math may be a required component of a skills package, the attainment of which is certified by the educational institution. In both cases, the only important indicator of math knowledge is the final grade for the required course. The ontology of math as a skill set and the epistemology of attainment through course completion, makes the question of “active learning” completely irrelevant from this quadrant’s perspective. On a transcript, a grade of “A” achieved solely through memorization and “exam prepping” is completely equivalent to an “A” achieved through active learning. A mindful teacher needs to be keenly aware of the perspectives from which the students view math, and how these perspectives affect the students’ goals. A student may come to the classroom with the LR view of “I need to get a passing grade in math, so I can get my certificate so I can get that job”. This student may not appreciate the teacher’s efforts at transformative learning. In order to arrive at a point of mutual understanding and mutual goals, the student as well as the teacher must lay their perspectives on the table – and the question “What is math?” could provide an excellent point of departure.
In this chapter, we used multiple theoretical models as lenses to conceptualize the notion of active learning in mathematics. Active learning can take place in different forms, and thus a mindful mathematics teacher must recognize what is the appropriate space for such activeness in every strand of learning and in every quadrant of the model.
This research was previously published in the Handbook of Research on Active Learning and the Flipped Classroom Model in the Digital Age edited by Jared Keengwe and Grace Onchwari, pages 177-194, copyright year 2016 by Information Science Reference (an imprint of IGI Global).
Bonwell, C., & Eison, J. (1991). Active learning: Creating excitement in the classroom (ASHE–ERIC Higher Education Rep. No. 1) . Washington, DC: The George Washington University, School of Education and Human Development.
Davis, B. (1996). An ear to the ground—The subject matter. Teaching mathematics: Toward a sound alternative (pp. 55–127). New York, New York: Garland Publishing, Inc.
De Corte, E., Verschaffel, L., & Depaepe, F. (2008). Unraveling the relationship between students’ mathematics-related beliefs and the classroom culture. European Psychologist , 13(1), 24–36. doi:10.1027/1016-9040.13.1.24
Denscombe, M. (2010). The good research guide for small-scale social research projects (4th ed.). Berkshire, England: Open University Press.
Edwards, M. (2005). The integral holon: A holonomic approach to organizational change and transformation. Journal of Organizational Change Management , 18(3), 269–288. doi:10.1108/09534810510599425
Esbjörn-Hargens, S. (2006a). Integral education by design: How integral theory informs teaching, learning, and curriculum in a graduate program. ReVision , 28(3), 21–29. doi:10.3200/REVN.28.3.21-29
Esbjörn-Hargens, S. (2006b). Integral research: A multi-method approach to investigating phenomena. Constructivism in the Human Sciences , 11(1), 79–107.
Esbjörn-Hargens, S. (2009). An overview of integral theory: An all-inclusive framework for the 21st century. Integral Institute Resource Paper , 1, 1–24.
Esbjörn-Hargens, S. (2011). Ontology of Climate Change: Integral pluralism and the enactment of multiple objects. Journal of Integral Theory and Practice , 5(1), 143–174.
Givvin, K., Stigler, J., & Thompson, B. (2011). What community college developmental mathematics students understand about mathematics, part 2: The interviews. MathAMTYC Educator , 2(3), 4–18.
Prince, M. (2004). Does active learning work? A review of the research. The Journal of Engineering Education , 93(3), 223–231. doi:10.1002/j.2168-9830.2004.tb00809.x
Renert, M., & Davis, B. (2010). Life in mathematics . In Walshaw, M. (Ed.), Unpacking pedagogy: New perspectives for mathematics classrooms (pp. 177–199). Charlotte, North Carolina: Information Age Publishing Inc.
Schoenfeld, A. (1989). Explorations of students’ mathematical beliefs and behavior. Journal for Research in Mathematics Education , 20(4), 338–355. doi:10.2307/749440
Star, J. (2005). Reconceptualizing procedural knowledge. Journal for Research in Mathematics Education , 36, 404–411.
Varela, F., & Shear, J. (Eds.). (1999). The View from Within. First person approaches to the study of consciousness . Exeter, UK: Imprint Academic.
Wieschenberg, A. (1994). Overcoming conditioned helplessness in mathematics. College Teaching , 42(2), 51–54. doi:10.1080/87567555.1994.9926820
Wilber, K. (1993). Spectrum of Consciousness . Wheaton, IL: Quest.
Wilber, K. (2000a). A theory of everything: An integral vision for business, politics, science, and spirituality . Boston, Massachusetts: Shambhala Publications, Inc.
Wilber, K. (2000b). Integral psychology: Consciousness, spirit, psychology, therapy . Boston, Massachusetts: Shambhala Publications, Inc.
Wilber, K. (2006). Integral spirituality . Boston, Massachusetts: Shambbala Publications, Inc.
Willingham, D., Nissen, M., & Bullemer, P. (1989). On the development of procedural knowledge. Journal of Experimental Psychology. Learning, Memory, and Cognition , 15(6), 1047–1060. doi:10.1037/0278-7393.15.6.1047
Yuen, C. (2013). Mathematics Anxiety Learning Phenomenon: Adult Learner’s Lived Experience and its Implications for Developmental Mathematics Instruction [Doctoral Dissertation]. University of Calgary, Calgary, Alberta, Canada.
AQAL: Stands for “All Quadrants All Levels,” but it also extends to the idea of “all quadrants, all levels, all lines, all states, and all types” and it refers to the comprehensiveness and integrity of approaching to a phenomenon.
Integral Learning (Edwards): A model describing learning as a cyclical process in which conceptual and behavioral knowledge is acquired through a number of iterative phases. The model consists of four learning strands, each corresponds to the four quadrants in the Integral Model.
Levels (in Integral Model): The complexity of the psychosocial phenomenon in each of the basic quadrants, generally referred to as the levels of developments in the left-hand quadrants and the levels of complexities in the right-hand quadrants.
Mathematical Concept: Focuses on the concept and the inner workings of a mathematical idea, essentially the prototypical response to “Why does a mathematical idea work in this fashion?”
Mathematical Procedure: Focuses on step-wise nuances of solving mathematical problems and the presentation of solutions, essentially the prototypical response to “how to solve a mathematical problem?”
Mindful Mathematics Teacher: The careful observations of the learning, in all its modes, as it happens minute by minute in the classroom, requires a degree of mindfulness on the part of the teacher.
Quadrants: UR, UL, LR, LL (in Integral Theory): The four co-arising perspectives (individual-interior, individual-exterior, collective-interior, and collective-exterior), each irreducible, with its own valid claim, and with its mode of investigation.
Stages or Mentalities of Mathematics: Developed by Renert and Davis, referring to the different types of mathematics taxonomized based on the extent of formality, style, and abstraction of mathematical ideas, objects, conjectures, and theorems.
1 For readers who are not too familiar with calculus, the position and velocity functions of an object are connected through differentiation, where the position function can be viewed as and the velocity function can be viewed as
or
.
2 There are further levels beyond level 6. For further details, please refer to Wilber (2000b).