The process of providing effective ongoing professional development to teachers is an arduous task for educational leaders. In areas, such as mathematics, professional learning opportunities must deepen teachers’ knowledge of content, pedagogy, and other skills connected to teaching. This chapter provides an examination of what teachers learned during a professional development project that was designed based off of principles for Learner-Centered Professional Development and addressed components of the Mathematical Knowledge for Teaching framework. The project included 3 half-day meetings with classroom-embedded activities completed between workshops. An inductive, thematic analysis of workshop evaluations indicated that teachers’ learning related to: a) a deeper understanding of the Common Core Mathematics Standards, b) exploring mathematical tasks, and c) planning lessons that start with mathematical tasks instead of direct teaching.
Professional development has the potential to substantially impact the quality of teaching and learning in schools (Loucks-Horsley, Stiles, Mundry, Love, & Hewson, 2010). Yet, the literature base on teacher learning is full of a myriad of research studies that cite the importance and effectiveness of ongoing, intensive learning opportunities that last at least a year and require an investment of time and financial resources to develop teachers’ knowledge and skills (Heck et al., 2008). In large-scale analyses of national professional development project grants, the duration and length that teachers are in professional development had a positive influence on teachers’ enactment of new knowledge and skills (Banilower, Boyd, Pasley, & Weiss, 2006; Garet, Porter, Desimone, Briman, & Yoon, 2001; Heck, Banilower, Weiss, & Rosenberg, 2008). Yet, school districts do not always have the resources or opportunity to provide lengthy professional development to their teachers. To this end, what is the benefit, if any, of less intensive professional development experiences for teachers that do not include as many hours of professional learning opportunities?
Learner-Centered Professional Development (LCPD)
In the past two decades much has been published about professional development for teachers (Loucks-Horsley et al., 2007; Wei, Darling-Hammond, Andree, Richardson, & Orphanos, 2009). Still, there has not been a complete unanimous consensus about the specific components that are essential to provide the optimal learning experiences for teachers (Polly & Hannafin, 2010; Wei, et al., 2009). In 2000, educational leaders adopted the American Psychological Associations’ research-based learner-centered principles (Alexander & Murphy, 1998; APA Work Group, 1997) and coined the term learner-centered professional development (LCPD; Hawley & Valli, 2000; National Partnership for Educational Accountability in Teaching, 2000a, 2000b). LCPD programs are designed around the teachers’ individual and collective needs who are participating in the professional development.
In a synthesis of the LCPD Principles and research on teacher learning, Polly and Hannafin (2010) found that LCPD programs include the following components: a) emphasis on topics related to student learning or areas that students have difficulty learning (Hawley & Valli, 2000), b) teacher choice or selection of some of their learning activities (Loucks-Horsley et al., 2010), c) hands-on and active opportunities to develop knowledge of pedagogy and content (Garet et al., 2001; Loucks-Horsley et al., 2010), d) collaborative activities with others (Glazer, Hannafin, Polly, & Rich, 2009; Hawley & Valli, 2000), e) ongoing activities that occur multiple times (Heck et al., 2008), and f) experiences to reflect on their teaching and their students’ learning after trying out pedagogies in their classroom (Borko, 2004).
Prior professional development projects that align with the components of LCPD have been empirically linked to teachers’ enactment of pedagogies emphasized during the professional development (McGee, Wang, & Polly, 2013; Polly, 2011a; Polly & Hannafin, 2011; Polly, McGee, Wang, Lambert, Pugalee, & Johnson, 2013; Fennema, Carpenter, Franke, Levi, Jacobs, & Empson, et al., 1996; Garet et al., 2001; Heck et al., 2008), gains in teachers’ content knowledge (Polly, Neale, & Pugalee, 2014; Wang, Polly, Lehew, Pugalee, Lambert, & Martin, 2013), and a positive impact on their students’ learning (Polly et al., 2013; Wang et al., 2013; Carpenter, Fennema, & Franke, 1996; Fishman, Marx, Best, & Tal, 2003; Heck et al., 2008).
While LCPD programs can improve teaching and learning, each of the projects that aligns with LCPD have included ongoing professional development projects that have included at least 60 hours of workshops or learning experiences in teachers’ classrooms. This chapter examines a professional development project aligned with LCPD, but with only 12 hours of professional learning experiences.
LCPD in Elementary School Mathematics
Professional development programs focused on elementary school mathematics must address the broad aspects of knowledge that teachers draw on when they teach mathematics (NCTM, 2014; Loucks-Horsley et al., 2010). Knowledge frameworks that have influenced the design of professional development include the construct of Pedagogical Content Knowledge (PCK; Shulman, 1987) and the Mathematical Knowledge for Teaching (MKT) framework (MKT; Ball, Thames, & Phelps, 2008).
Pedagogical Content Knowledge
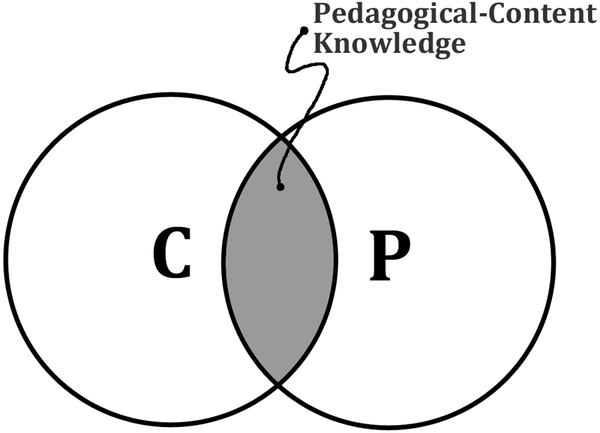
Schulman’s seminal work posited that effective teachers draw on knowledge of general pedagogy, content, and a knowledge construct that reflects the intersection of pedagogy and content. The double venn diagram (Figure 1) reflects the construct. PCK was developed to be independent of subject areas, meaning that elementary school teachers may have PCK for literacy, mathematics, science, and social studies.
| Figure 1. Pedagogical content knowledge framework |
|---|
 |
| (Mishra & Koehler, 2006) |
In mathematics, PCK in the classroom is content specific compared to general pedagogical knowledge (PK). For example, consider two teachers working on subtraction with their second grade students. The first teacher facilitated a class discussion of students’ strategies by asking students to share how they solved the problem. This would be an illustration of general pedagogical knowledge (PK), since in all subjects it is reasonable to have students share their answers and how they found the answer. However, another teacher had students share how they solved the problem, and then followed the conversation by leading a discussion about the question, “Which of these strategies relates to what we know about place value with tens and ones?” This question and the teachers’ facilitation of a discussion reflects pedagogical content knowledge (PCK), since the conversation is now focused on a specific aspect of mathematics.
Studies related to PCK have indicated a gray area between research-based pedagogies and what some may consider ineffective pedagogies (Polly, 2011b). Specifically, if a teacher repetitively gives students a plethora of low-level questions on worksheets and facilitates the conversation about mathematics, these pedagogies are not ideal, nor are they research-based, but still relate to the intersection of mathematics content and pedagogies. When designing LCPD programs in mathematics, PCK can help frame the design of learning activities if professional development facilitators acknowledge the need for activities to focus in the center of the double venn diagram, and align to both content and pedagogy as much as possible.
Mathematical Knowledge for Teaching
Seeking a mathematics-specific framework for teaching, the Learning Mathematics for Teaching group at the University of Michigan developed a research-based framework on the knowledge that teachers draw on when they teach mathematics (Ball, Thames, & Phelps, 2008). The diagram in Figure 2 reflects the framework.
| Figure 2. Mathematical knowledge for teaching framework |
|---|
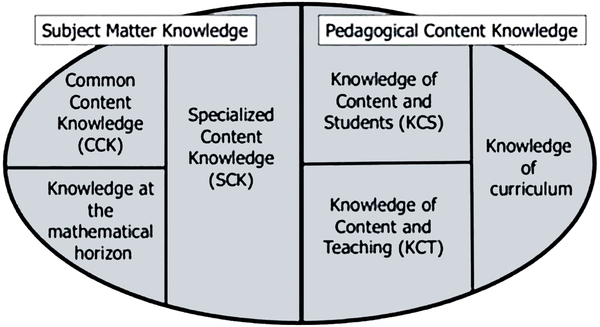 |
| (Thames & Ball, 2010) |
The left side of Figure 2 reflects content knowledge which has been split into three areas, common content knowledge which are general definitions, a strategy to solve a problem, or mathematical knowledge that is not specifically connected to teaching. Knowledge at the mathematical horizon encompasses content knowledge that is related to other concepts, such as repeated addition and multiplication. Multiplication is on the mathematical horizon of addition for teachers in Grades 1 and 2. Lastly on the left side, the specialized content knowledge refers to knowledge of various mathematical representations and strategies to solve problems that are less common, including using tools such as hundreds boards, number lines, or alternative algorithms based on place value concepts.
The right side of the diagram reflects what Schulman would have referred to as pedagogical content knowledge (Thames & Ball, 2010). In terms of pedagogies, there is a need for teachers to know the curriculum, which includes grade-level specific standards and curricular resources that are available. The knowledge of content and teaching refers to how to teach specific content in various ways, including knowledge of tools, strategies and resources to draw on. The knowledge of students refers to how students typically come to understand or where they struggle as it relates to specific mathematics concepts.
Researchers working on the MKT framework based this framework off of extensive video analyses of mathematics teaching, interviews, and surveys with teachers. Further, they developed and validated an instrument to assess teachers’ MKT and found that teachers’ scores were positively associated with gains in student learning (Hill & Ball, 2004).
MKT provides a framework for professional development facilitators as it provides a more specific set of components than the PCK framework, which is more general. While there are more components of MKT than PCK to address during the design and implementation of professional development, it is reasonable to expect that all aspects of the MKT can be addressed to some extent during a professional development program.
Description of the Professional Development Program
Each teacher participated in a 12-hour professional development experience that included 3 face-to-face workshops that were 3 hours each and 3 hours of classroom-embedded professional learning activities. The content of these workshops and classroom-embedded activities were decided by district leaders and the author, and aligned to the MKT framework (Table 1) and the LCPD Principles (Table 2).
Table 1. Description of Professional Development Content
| Professional Development Activity | Focus | Focus from the MKT Framework |
|---|---|---|
| Workshop 1 | Focus: Solving cognitively-demanding mathematical tasks, unpacking grade-level Standards, strategies to teach specific concepts. | Specialized content Knowledge, Knowledge of Curriculum, Knowledge of Content and Teaching, Knowledge of Students |
| Classroom-embedded activity after Workshop 1 | Select or design then pose a cognitively-demanding mathematical task to your class. Examine students’ mathematical thinking during the lesson and their work after the lesson. Bring the task to Workshop 2. | Knowledge of Content and Teaching, Knowledge of Students |
| Workshop 2 | Focus: Unpacking grade-level standards, Examining curricular resources, Designing a lesson using the Thinking Through a Lesson Protocol (TTLP) Other: Solving mathematical tasks, strategies to teach specific concepts. |
Specialized Content Knowledge, Mathematics at the Horizon, Knowledge of Curriculum, Knowledge of Content and Teaching, Knowledge of Students |
| Classroom-embedded activity after Workshop 2 | Design a full mathematics lesson that follows the TTLP. Examine students’ mathematical thinking during the lesson. Bring back student work to Workshop 3. | Knowledge of Content and Teaching, Knowledge of Students |
| Workshop 3 | Focus: Examine student work, consider students’ mathematical thinking related to their lesson, develop a rubric for the lesson they taught. Other: Solving mathematical tasks, unpacking grade-level Common Core Standards, strategies to teach specific concepts |
Specialized Content Knowledge, Mathematics at the Horizon, Knowledge of Curriculum, Knowledge of Content and Teaching, Knowledge of Students |
| Classroom-embedded activity after Workshop 3 | Modify the lesson for future use and upload to Google Drive to share with district leaders. | Knowledge of Content and Teaching, Knowledge of Students |
Table 2. Alignment of the Project to LCPD
| LCPD Principle | Description of Alignment |
|---|---|
| Focused on student learning | All activities focused on the critical areas of the Common Core Mathematics Standards. |
| Teacher ownership | Teachers chose what Standards or concepts that they wanted to work with for the classroom-embedded activities. |
| Active learning of knowledge of content and pedagogy | Teachers solved mathematical tasks, examined their grade-level Standards, and analyzed various strategies to solve math problems. |
| Collaboration | Teachers collaborated in every aspect of the workshop. |
| Ongoing | Teachers met for 3 3-hour workshops across a 7 month period. |
| Reflective | Teachers spent time in Workshop One reflecting on how their students were doing generally in mathematics. In Workshops Two and Three they reflected on their experiences posing cognitively-demanding mathematical tasks and teaching lessons that started with a task. |
Below are descriptions of the professional development experiences that were included in the project.
Solving Cognitively-Demanding Mathematical Tasks
Teacher-participants solved cognitively-demanding mathematical tasks (NCTM, 2014; Stein & Smith, 1998) that were multi-step and often open-ended with multiple correct answers during each workshop. The topics embedded in each of the tasks were related to the grade level’s Common Core Mathematics Standards and included both specialized mathematical knowledge as well as mathematical knowledge on the horizon for teachers. All of the tasks posed would be categorized as cognitively-demanding based on the mathematical task framework (NCTM, 2014; Stein & Silver, 1988).
During workshops, the process of task exploration included allowing teachers to collaboratively explore tasks, discuss with others strategies that their group used to solve tasks, analyzing strategies as a whole group, and then brainstorming modifications to the task to better align the task to their grade-level standards, support task exploration for struggling students, and provide extensions to the task for high performing students. Throughout the exploration of mathematical tasks, the author posed tasks and supported task exploration, as teachers might, by posing clarifying questions such as, “What is the problem asking you?” and “How can the information that you have help you solve this task?”
For example, in a Grade 1 workshop teachers explored the following task, which was adapted from the YouCubed website (http:///www.youcubed.org; Stanford University, 2015). A bunny rabbit can hop either 1 foot or 2 feet at a time. How can the bunny travel a total of 6 feet? Find as many possible answers using either manipulatives or pictures to prove your work. While exploring this task, teachers used snap cubes, graph paper, or unlined printer paper to represent the problem. In some cases, teachers also provided an equation. For instance, 6 jumps of 1 foot would be represented by 1+1+1+1+1+1=6, while 3 jumps of 2 feet each would be represented by 2+2+2=6.
After strategies were shared and analyzed, teachers worked together to modify the task to create ideas for struggling and high performing students. Students talked about the importance of representations and tools, such as number lines, the cubes that they used, or other strategies, as well as how they may make the total distance traveled larger for some students. Teachers also worked with math on the horizon as some teachers tried to figure out algebraically how many actual solutions there were to make sure that they found them all.
An outcome of the first workshop for each grade level was for teachers to select or design and then implement a cognitively-demanding mathematical task to their students. They discussed this experience during the second workshop and this idea of cognitively-demanding tasks was discussed in depth during both the second and third workshops.
Unpacking Grade-Level Standards
During each of the workshops teachers spent time analyzing their grade level Unpacking the Common Core Mathematics Standards document that had been written by the <state blinded> Department of Education’s Mathematics Department. The Unpacking document provides a description and examples for each Standard, and is the state’s starting point for creating assessments. In the workshops, the author would often pose a task or provide an activity for teachers and then have teachers determine which Standard(s) it aligned to. These activities, many teachers reported, were the first times that they looked at the Unpacking document or spent time focused on which Standards specific activities align to.
As teachers were discussing the Standards, the author posed questions about the connections or relationships between Standards in earlier and later grades in order to provide a vertical focus of the mathematics concepts. For example, in the first Grade 2 workshop teachers were looking at the expectations for subtraction fluency. The author asked the questions, “What experience have students had in previous grades?” and “What are the expectations in Grade 3 related to these concepts?” These questions and the process of examining and discussing prior and future grades’ Standards help teachers to better understand how the Standard in their grade level aligned and fit into students’ development of those mathematics concepts.
Strategies to Teach Specific Concepts
As part of every workshop teachers solved tasks using multiple strategies with a focus on concrete/hands-on, pictorial, and symbolic/equation focused strategies. Teachers had concrete manipulatives and paper readily available in every workshop and were encouraged to solve tasks using all concrete, pictorial, and symbolic strategies. After solving tasks in these different ways, there were discussions about the mathematical knowledge that students would need in order to use each strategy successfully.
Further, many teachers brought up the question about what they should do if students struggled using a specific strategy. For example, in the second Grade 5 workshop teachers were working on multiplying fractions using graph paper to draw pictures of the situation. One teacher asked, “If my students can’t draw pictures but can just use an algorithm why do they need the picture?” The author asked the room of teachers for responses, which led to a 20-minute conversation about the benefit of having students to use pictures to support their understanding of the algorithm.
Thinking Thru a Lesson Protocol
The Thinking Thru a Lesson Protocol (TTLP; Stein, Bill, & Hughes, 2008) is a research-based process of developing a mathematics lesson plan. The protocol starts by unpacking Standards and identifying mathematical goals for the lesson. Next, the teacher selects a cognitively-demanding mathematical task to pose to start the lesson, and considers the strategies that students may use as well as their potential struggles and how to support students through questioning. The TTLP also includes aspects of brainstorming questions to ask to lead a discussion of the task as well as follow-up tasks and activities to provide further experiences with the mathematical concepts.
During the second workshop for each grade level, the author used an abbreviated form of the TTLP and focused on the idea of starting the lesson with a cognitively-demanding mathematical task prior to any modeling or direct teaching. This was a concept that was different from teachers’ typical way of planning a lesson, which led to a lot of discussion about the rationale behind this approach and the potential benefit to students of doing mathematics at the beginning of a lesson instead of watching the teacher instruct and model strategies. The outcome of the second workshop was for teachers to return to their classroom to teach a lesson that they had collaboratively planned using the abbreviated TTLP format. They were charged with bringing back student work and their lesson to the third workshop to debrief and reflect.
Analyzing Student Work
Based on the lesson that teachers taught after Workshop 2 they returned to Workshop 3 with student work from the lesson that they taught. Teachers spent time in Workshop 3 trading student work with their colleagues that they collaboratively planned with, and spent time examining students’ varying strategies. The discussion led teachers to discuss where students struggled, succeeded, and what teachers did in that lesson and subsequent lessons to support students’ learning.
In the workshop, the author then facilitated the process of creating a rubric with teachers. First, teachers sorted their student work into three piles, student work that teachers felt met the benchmark or expectations for the lesson, student work that partially met the benchmark, and student work that did not meet the benchmark. Based on these sorts, teachers then came up with descriptive statements for work that met, partially met, and did not meet the benchmark. Due to time constraints, the rubrics were not fully developed, but the activity closed with teachers discussing with one another about how they might grade or score the work samples that they collected using the descriptive statements.
Research Questions
This chapter examines what teachers took back to their classroom from a Learner-Centered Professional Development (LCPD) program that was framed around the Mathematical Knowledge for Teaching (MKT) framework. The design of the study used an iterative process influenced by design-based research. Feedback was collected after each of the 3 half-day meetings and the professional development design was influenced by the feedback. Based on the designs, this study covers the following research questions:
This study includes an iterative design, in which teacher feedback was collected after each of the three half-day professional development workshops that was held. This section describes the professional development, data sources, and the process of data analysis.
Context
The professional development project was implemented in a large suburban school district just outside of a major city in the southeastern United States. The district had not had any district-wide mathematics professional development in the past 5 years, and their scores on the state End-of-Grade tests had either plateaued or dropped after the adoption of the Common Core State Standards during the 2012-2013 school year. The district includes 30 elementary schools who educate students in Grades Kindergarten through Grade 6. Student performance on mathematics and reading tests is above the state average, but there is a history of low performance on state end-of-grade tests for students who are African-American and Hispanic. Further, while many schools have a high percentage of students who pass the state test annually in Grades 3-5, the amount of student growth has not been high in recent years.
In the fall of 2014, district leaders contacted the author about ways to support teachers’ mathematics instruction. Based on limited resources and the interest in designing and implementing professional development during the 2014-15 school year, district leaders and the authors agreed to hold a series of professional development workshops with follow-up activities during the year. Workshops were grade-level specific, and one teacher per grade level per school attended. Some schools also sent building-level instructional facilitators as well.
Data Sources and Analysis
Written feedback from teacher-participants was the primary data source for this study. Written feedback was collected after each workshop in response to the questions, “What did you learn from this workshop?” Further, notes from the author following the workshops and conversations between the author and district leaders were treated as secondary data analyses.
All data was analyzed using an inductive, thematic process (Coffey & Atkinson, 1996). For question one, data was entered into a spreadsheet with column headers as a) the workshop number, b) grade level, c) the written teacher feedback. The teacher feedback was then analyzed using an open-coding process. Following the first round of coding the data, codes were consolidated if they were similar. For example, teaching diverse learners and differentiating instruction were combined into the code differentiation for diverse learners. Once codes were consolidated, the author reviewed the data within each code to identify frequently occurring ideas which became themes. The themes were then verified by revisiting the original data source.
For question two, data analysis included summarizing the findings for question one as well as notes recorded by the author after workshops, and notes from conversations between district leaders and the author. These findings are summarized in the findings section in order to provide perspective about the decisions on what would be emphasized and included in future workshops.
Data analysis indicated several findings. In the following section, I summarize and include data excerpts that were the most prominent.
Question One: What Teachers Learned
As shown in Table 1, Workshop One for all grade levels focused on teachers’ solving cognitively-demanding mathematical tasks, analyzing the Unpacking the Common Core Standards document, and considering various strategies for teaching mathematics. Data analysis indicated themes related to solving mathematical tasks, strategies to teach concepts, and understanding the standards.
Solving Mathematical Tasks
A theme found in the feedback from all grade levels was the level of rigor in the mathematical tasks that they explored during workshops. Teachers included comments, some positive and some negative, about the amount of mathematical thinking that they were forced to engage in, as well as the level of rigor expected in the Common Core Mathematics Standards.
A Grade Five teacher wrote,
I did not expect to come to a half-day workshop and do so much math. The tasks were hard, multiple step, and well beyond what I feel that my students can do. Yet I see the point about how the expectations for my students need to be high.
A Kindergarten teacher wrote, “When we solved the tasks on place value and the number system I saw where I had some misconceptions about how our number system works. It helped me to feel like my students do when they do hard math.”
Both of the teachers’ comments above focus on the mathematical content knowledge aspects of the Mathematical Knowledge for Teaching (MKT) framework. Teachers on the whole felt that the mathematics that they had to do in the workshop deepened their own understanding of mathematics related to what they taught. As seen above in the fifth grade teacher’s comment, though, some teachers did not report seeing a clear connection between the mathematical tasks in the workshop and their grade level standards and curriculum.
To that end, a Grade One teacher wrote, “I get the idea of working on multi-step subtraction with larger numbers. However, I did not see how it connects to the work that we do since we work primarily with smaller numbers.”
Comments coded in the rigor category echoed these statements, where teachers did not report positive feedback about working with mathematics concepts on the horizon.
Strategies to Teach Concepts
Workshop One also included opportunities for teachers to use, discuss, and analyze strategies to teach concepts, which focuses on the Knowledge of Teaching and Content aspect of the MKT framework. The data in this code varied; some teachers reported learning brand new strategies to teach the concepts that were included in the workshop, while some teachers reported having had experiences prior to the workshop and that the strategies were simply a repeat.
A Kindergarten teacher said, “The idea of solving word problems using counters on number lines and ten frames was a new idea to me. I had used counters by themselves, but not with other tools.”
A Grade Four teacher said, “The strategies that we used to work on multi-digit multiplication will help me as I go back and review this work with my students. It would have been nicer to have this at the start of the school year.”
Other teachers felt that they did not gain any new strategies. A Grade Five teacher commented, “I had already seen these strategies from my instructional facilitator. It was obvious others in the room needed them, but I didn’t get anything new from this.”
Further, a Grade Two teacher said, “The Unpacking document has all of these strategies. While it was nice to discuss these as a group today, I could have gotten the same ideas by reading from it.”
The data coded as strategies included a mix of comments such as the ones above. Based on the fact that administrators had nominated various ranges of teachers, some expert and some novice to attend, the teachers in the room had varying backgrounds which influenced their experience.
Understanding the Standards
All of the data coded related to standards was positive as all of the data sources reported gaining a better understanding of their grade level expectations. Teachers reported getting a better sense about the goals and rationales of the Standards as well as what students should be able to do in order to demonstrate that they have met the Standards.
A fifth grade teacher wrote,
The benefit of today was a better understanding of the expectations for decimal work and exponents. I had taught these standards at a more basic level than what we discussed today so I can go back and now increase the rigor of what we are doing.
Further, a Kindergarten teacher noted, “I have been teaching a lot of first grade content. My students are very good at math, but today gave me ideas on how I can be sure that my students have mastered the Kindergarten concepts.
Both of the teachers above shared that they learned more about the grade-level specific expectations. Teachers reacted in the workshops as if they had not seen the state Unpacking documents before, and this was their first experience looking at descriptions and examples of the Standards.
Summary of Workshop One
Workshop One focused heavily on exploring cognitively-demanding mathematical tasks, analyzing the state Unpacking the Common Core Standards documents, and exploring strategies to teach the mathematics concepts. Teachers’ feedback varied, as some teachers reported that they learned more about their grade-level standards, and the level of rigor expected in their classrooms. However, some teachers reported negative comments about doing mathematics that was on the horizon and not closely connected to concepts in their grade-level as well as comments about seeing strategies that they have already seen and use in their classroom.
Question Two: Plans for Workshop Two
When the author and district leaders reviewed feedback and made plans for Workshop Two, the group agreed to focus more on the design and planning of mathematics lessons. District leaders reported the district-wide need for teachers to experience and work on planning lessons that were focused more on cognitively-demanding mathematical tasks and less on teachers modeling and demonstrating to students how to solve problems.
Further, district leaders reported that there should be a continued emphasis on mathematical strategies that include concrete and pictorial ways to solve problems. District leaders pointed out that while teacher feedback indicated that some teachers already knew some strategies, these approaches to solving problems were not being consistently observed in classrooms. For workshop two, there was an intentional decision to have teachers solve problems with an algorithm as well as other strategies and better understand why the algorithm works as it relates to other strategies and approaches. Further, district leaders gave the author the standards and concepts that teachers would be teaching so that the mathematical tasks better aligned to what teachers were currently or what they would be teaching.
Another decision that was made for Workshop Two was to allow teachers to have adequate time to collaboratively plan a lesson that they would then go back and teach, and hold them accountable for collecting student work for Workshop Three. While this was part of the original plan, the use of the abbreviated TTLP framework and what teachers would do in their classroom was not decided until after Workshop One.
Question One: What Teachers Learned
Workshop Two focused on the planning and design of a mathematics lesson that was built around starting with a cognitively-demanding mathematical task. Further, activities that were focused on during Workshop One, including mathematical tasks, unpacking the standards, and analyzing strategies, were still included in the workshop. Data analysis indicated themes about planning a lesson, solving mathematical tasks, and understanding the standards.
Planning a Lesson
All of the data associated with the code planning included comments from teachers in which they learned more about planning a math lesson focused on mathematical tasks. These comments aligned to the Knowledge of Teaching and Content and Knowledge of Students of the MKT framework. All comments in this code included teachers reporting that this approach to teaching mathematics was different from how they teach.
A Kindergarten teacher wrote, “I am used to modeling a lot up front. By giving them a problem to solve to start math is going to come across as unusual. I hope they are o.k. with it.”
A Grade Two teacher commented, “There seems like a lot of benefit in getting students doing math problems at the start of a lesson. I am excited about trying this and seeing how they do with it.”
Some teachers reported more skepticism about this approach to teaching mathematics. Most of the skeptical comments were in Grades 3 through 5, where there is a high-stakes state test at the end of the year.
A Grade Four teacher wrote,
This idea of starting a lesson with a math task, discussing it and then posing more math tasks is so different than what I do know. My students may struggle a lot with the problem solving process and want me to help them a lot.
A Grade Five teacher wrote, “I learned about this starting with a task approach. My students need a lot of modeling and up front teaching so I don’t think they will do well. I will try it once but they will struggle.”
As part of the professional development program requirement teachers collaboratively planned a lesson using the abbreviated TTLP and started the lesson with a cognitively-demanding mathematical task. As seen above in the quotes teachers reported a range of feelings about this idea of starting with a task instead of direct teaching.
Solving Mathematical Tasks
Similar to the feedback from Workshop One there were multiple comments about teachers’ experiences solving mathematical tasks, which aligned with the Knowledge of Specialized Mathematics and Knowledge of Mathematics on the Horizon from the MKT framework. Teachers’ comments were more positive than the Workshop One comments about mathematical tasks.
Grade Five teachers, which were especially negative about solving so many tasks during Workshop One, reported more positive comments about solving tasks in Workshop Two focused on multiplying fractions.
One Grade Five teacher wrote,
I am about ready to start teaching this concept so it was helpful to solve some very hard problems in a few different ways to help me grasp the content. I have a sense now on what I need to do during my unit.
Another Grade Five teacher commented, “Solving these hard tasks is more beneficial to us when we are in the midst of or about to teach this in our classroom. The tasks were a better fit today than the first workshop.”
Teachers in all grade levels reported benefit in solving tasks prior to looking at the Standards. One Kindergarten teacher wrote, “I learned more about the relationship of addition and subtraction by doing the opening task. From there when we got into Kindergarten standards it made more sense on how I can use addition to help students better understand subtraction.”
Some teachers reported learning about the rigor involved with mathematical tasks and shared connections to their classroom-embedded assignment of posing a cognitively-demanding task to their students. A Grade Three teacher wrote,
Having posed harder problems to my students since the first meeting I now have a better appreciation for how my students feel. I am learning myself how to approach these problems and the value that I and my students get by struggling through some tasks and figuring out how to solve them. [The author] doesn’t give us strategies and it makes it harder, but when I am able to solve the task I feel like I have learned more compared to if he had just said, ‘here is how you do it.
Understanding the Standards
Data from Workshop Two related to Understanding the Standards focused on teachers learning more clarification of Standards from the state Unpacking the Common Core Standards document that was confusing to teachers. This aligned to the Knowledge of Curriculum and Knowledge of Students aspects of the MKT framework. One Kindergarten teacher stated, “The various types of subtraction situations is hard to determine. It helped to spend time looking at the Unpacking and determine what my students need to learn this year and what can wait until next year.”
A Grade Three teacher noted, “The work that we did today on division problem types was helpful. I had no idea that some of those situations were things that I should cover with my students.”
In some cases teachers reported learning about the Standards in light of using resources that were not aligned to the Standards.
A Grade five teacher noted,
A lot of the resources that we use in our school do not focus as much on the ideas in the Unpacking document. I now know that we need to be more careful about choosing lessons and activities to make sure that they align to the Standards.
A Kindergarten teacher noted, “The tasks that my grade level gives are way above Kindergarten standards. It will be good to go back and talk to them about making sure that our activities align to what our students should be doing.”
Teachers’ comments that aligned to this code focused on better understanding grade level expectations and the alignment of resources. As teachers studied the standards more they reported developing a deeper understanding of the grade-level expectations for their students and a stronger sense on what good activities look like to address those standards.
Summary of Workshop Two
Teachers’ feedback from Workshop Two focused on planning a mathematics lesson, which was a new theme, and two old themes, solving mathematical tasks and understanding the standards. Teachers reported that the planning process in the workshop was new to them, and some expressed skepticism and comments that could be viewed as negative. Teachers’ wrote positive comments about mathematical tasks and the standards. Some teachers commented that they saw a stronger connection to solving mathematical tasks and their teaching since the tasks in the workshop aligned to the content that teachers were working on.
Teachers also reported that they learned more about the specifics of the Common Core Mathematics Standards. Some teachers referenced that they had their understanding of types of problems clarified, while some teachers made the connection that some curricular resources that they were using did not align well to the actual Standards.
Question Two: Plans for Workshop Three
The feedback from Workshop Two was more positive than the feedback from Workshop One. The author and district leaders felt that focusing on concepts that they were in the midst of or preparing to teach was one of the key factors to the positive feedback. The group, however, did acknowledge the skepticism and slight negativity about teaching mathematics through a task-based approach using the abbreviated TTLP framework. As a result, they made an intentional decision to revisit the TTLP framework and process of planning a lesson during Workshop Three. They also made the decision to provide teachers with opportunities to examine lessons and resources and be evaluative about their alignment to both the Common Core Standards as well as the idea of teaching more with mathematical tasks and less with direct instruction.
The group also decided that the focus on assessment should still be central to the activities, and that teachers should have some experiences looking at student work, analyzing students’ strategies, and collaboratively reflecting on how their lesson went, especially this approach to teaching a lesson by starting with a mathematical task. The plans for Workshop Three also included a great deal of conversation about whether or not teachers should write another lesson plan just to gain practice. While the group felt that that would be beneficial, a full plan was not written in order to keep the focus on assessment.
Question One: What Teachers Learned
Workshop Three focused on examining student work from teachers’ classrooms as well as looking at what it means to assess students’ mathematical thinking. Teachers spent a good bit of time examining students’ strategies, talking about what examples met their benchmark, and then discussing what assessment could look like in their grade level. Teachers’ feedback about what they learned after workshop three focused on four themes. Two themes were new: students’ strategies and assessing during teaching, while two themes were old, planning a lesson and solving mathematical tasks.
Students’ Strategies
Teachers’ feedback in this code focused on what teachers learned about the various ways to solve mathematical tasks. These comments align to the Knowledge of Students aspects of the MKT framework. As teachers spent time looking at each other’s students’ work there were many comments during the workshop that teachers were seeing strategies that their students had not used.
These were also reflected in the written feedback. For example, a Grade Two teacher wrote, “By looking at students’ work from other schools I noticed that their kids were using strategies to solving problems that I had not thought of before.”
Some of these comments focused on general problem solving processes, while some focused on specific strategies that were concept focused. A Grade Four teacher noted,
I learned from another teacher about the SOLVE strategy for solving word problems. One teacher in my group has all of her students use this process to identify what is in the problem, solve the problem, and then explain what their answer means.
A Grade One teacher also wrote, “I learned from another teacher today about how to use a part-part-whole mat to solve problems. It is a creative idea that I am going to try tomorrow.”
Some comments, however, focused on concept specific strategies. For example, a Grade Four teacher wrote, “A teacher in our group had her students use rectangles and number lines to solve their addition of fractions problems. By doing both, her students were able to check their work and make sure they got the right answer.”
A Grade Two teacher wrote, “I saw a lot of student work today with the open number line on it. I knew the strategy but thought it was too hard for my students. I want to try it now, though.”
Teachers’ comments about strategies included aspects of learning from their peers through the process of looking at student work. The collaborative process allowed teachers to discuss students’ strategies and how their lessons went. As a result, teachers realized that the collaborative lesson was taught in slightly different ways, which led to rich conversation about how students solved the tasks, and how teachers supported students’ thinking.
Assessing During Teaching
Another new theme that emerged during the feedback from Workshop Three was assessing during teaching, which sometimes is referred to as formative assessment. This aligns to the Knowledge of Students and Specialized Content Knowledge aspects of the MKT framework. Teachers reported that they had learned about ways to assess students while teaching a mathematics lesson.
While formative assessment is thought to be a more common practice in the younger grades, some primary grades teachers reported learning new processes. A Kindergarten teacher wrote, “I learned about ways to manage and structure my classroom to make it easier to assess my students while they are doing activities.”
A Grade One teacher wrote, “I typically assess all of my students at the end of the week or a unit, but I want to try these ideas of observing and filling out checklists on a more frequent basis.”
Teachers in the upper grades also reported learning about formative assessment, but the comments included more skepticism. A Grade Five teacher commented, “Ideally the idea of assessing students during work is nice, but with 28 students that range in ability, I don’t see how that will work. I learned some things that maybe I can try next year.”
A Grade Four teacher wrote, “Once I figured out how to make it work with my students I like the idea of assessing my students as they work. I have to think about how to actually make it happen in my classroom, though.”
Teachers’ conversations with each other and their process of considering how to assess students both after and during work on mathematical tasks led to teacher-reported learning about the ideas. However, teachers, especially those in upper grades, reported a need to consider and more thoughtfully think about how it would actually work in their classroom with their students.
Planning a Lesson
Planning a lesson was a theme after Workshop Two and also after Workshop Three. This theme aligned to the Knowledge of Teaching and Content and Knowledge of Students of the MKT framework. Here after Workshop Three, teachers reported more positive comments about planning a lesson by starting with a mathematical task than they had immediately after Workshop Two. Since teachers taught a lesson in this new manner between Workshop Two and Three, that experience could have led to their more positive comments.
A Grade One teacher wrote,
Having talked to others who were new to this format and thinking about my own time I learned more about how to support my students while they solve a task at the start of the lesson. I still feel the need to jump in and teach, but I want to try and stick to just asking questions to let students explore and solve the task.
A Grade Four teacher wrote,
Since I taught this way for the first time two months ago I have tried this approach at least a few times a week. I am getting more comfortable with it, and my students enjoy this much more than if I begin by teaching examples.
While a majority of the teachers were positive, some teachers still reported skepticism about the approach. A Grade Five teacher commented, “I feel that this approach works for some students, but not all. Some of my students depend on me to give them an example that they can follow before getting to work.”
Solving Mathematical Tasks
During Workshop Three teachers solved at least one cognitively-demanding mathematical task, even though the task exploration was not as much of a focus as in the two previous workshops. Still, comments from teachers reported learning that aligned to this code. This theme aligns to the Specialized Content Knowledge, Mathematical Knowledge on the Horizon, and Knowledge of Students aspects of the MKT framework. The data that aligned to this theme focused on learning multiple ways to solve mathematical tasks.
A Grade Four teacher wrote about a task about multiplying a fraction by a whole number.
I solved this task like I teach my students to by drawing multiple pictures of the same fraction and then counting pieces. When we talked about this at my table, though, a few teachers had drawn only one picture and used colors to indicate the multiplication. As we kept discussing this, I realized that their approach matches the problem better, and some of my students may see the concept better that way.
While feedback aligned to this theme in previous workshops focused more on the rigor and the experiences of solving tasks as learners, nearly every comment in this theme focused on teachers’ acknowledging either multiple approaches to solving the task or potential struggles that their students may have on a related task based on the concepts embedded in the task they were solving. A Grade Two teacher wrote about their experience exploring three-digit subtraction using various strategies.
The task that we did reinforced the idea that three-digit subtraction is much more complex than two-digits if we have to regroup in the hundreds, tens, and one’s places. The strategies that we talked about as a whole group helped me to see the potential struggles that my students will have if I only focus on the traditional algorithm.
Summary of Workshop Three
Workshop Three focused on looking at student work and considering assessment. Data analysis indicated that teachers reported learning new themes related to students’ strategies and assessing during teaching, as well as previous themes of planning a lesson and solving mathematical tasks. Teachers reported learning about the idea and processes of assessing during teaching, but some teachers were skeptical of how it would work in their own classroom.
Teachers’ feedback included connections between themes related to solving mathematical tasks and multiple strategies to solving tasks. Their comments about solving tasks during workshops acknowledged the benefit of solving a task in multiple ways as well as potential issues that their students may face.
Question Two: Plans for Future Professional Development
Since only three workshops were scheduled comments after Workshop Three focused on the next steps and directions for professional development as a whole. The group of the author and district leaders felt that while the 30 teachers per grade level, 180 in all, and the handful of instructional facilitators may have benefitted from the experience, this was just the beginning of ongoing mathematics professional development for teachers. There were, and still are, ongoing discussions about whether to repeat the experience with another 180 teachers, or to focus on a different set of professional learning experiences that could include these teachers and others who were interested as well.
Further, since district leaders had participated in the workshops and also attended other professional development on mathematics instruction, they felt that their capacity had been built to start facilitating summer workshops as well as professional development in the following year. While some had facilitated past workshops, most had not, so their feeling of being capable enough to design and lead professional development that was similar to what they had experienced was a positive outcome.
Based on the findings shared above in light of the LCPD Principles and the MKT framework there are some themes that warrant further discussion and have implications for future work. They include: a) the design of mathematics LCPD programs, b) classroom-embedded professional development activities, and c) addressing aspects of the MKT framework.
Design of Mathematics LCPD Programs
The LCPD Principles provide a research-based framework that informs the design of professional learning activities for teachers (Polly & Hannafin, 2010). The framework provides designers of professional development with components to include in programs (Polly & Hannafin, 2010, 2011). Table 2 provided an alignment between the project in this study and the LCPD framework. In the LCPD framework the only Principles mentioned refer to areas of student learning or where students tend to struggle and knowledge of pedagogy and content. Based on the themes in this study described earlier, teachers reported learning about areas related to student learning as well as knowledge of both pedagogy and content.
The only aspect of duration that did not completely align to LCPD Principles was the duration and number of hours in the professional development program. Past research indicates that LCPD programs with duration and an ongoing format lead to greater implementation of teachers’ practices and also student learning outcomes (Banilower et al., 2008; Garet et al., 2001). Banilower et al. (2008) found that generally 30 hours of professional learning are needed to influence teachers’ practices and 80 hours are needed to influence students’ learning. Based on the limitations of time and resources, this project only included a 12-hour professional development experience, which falls considerably short of both of those recommendations. Still, teachers reported learning a great deal about mathematics teaching and learning from their experience.
This study was limited in that it only looked at teachers’ reported learning. Based on teachers’ feedback, the LCPD program in this study shows potential in its impact on teachers. However, a more in depth study is needed. Subsequent research would be advantageous, specifically to examine teachers’ instruction through observations and other artifacts of practice as well as student learning through a common assessment.
Classroom-Embedded Professional Development Activities
While the past two decades have called for classroom-embedded professional development activities there has been little research that has specifically focused on the influence of professional learning that is embedded in teachers’ classrooms. This project included 3 one-hour experiences focused on classroom-embedded professional development, which included posing cognitively-demanding mathematical tasks, teaching a lesson that was focused on opening with a mathematical task and collecting student work, and refining the lesson for future use. These experiences aligned with the focus of the whole program and provided teachers with an opportunity to put into practice what they were learning.
At the end of Workshop Three teachers’ comments related to planning lessons were more positive than after Workshop Two. While some teachers still shared some skepticism, most teachers favorably reported about learning to plan lessons focused on starting with a cognitively-demanding mathematical task. This finding supports the results of the seminal Cognitively Guided Instruction project which found that some teachers’ beliefs about adopting new instructional practices did not change until teachers tried and used the practices with their own students in between workshops (Carpenter et al., 1996). More recent studies have also found that teachers need multiple times planning and teaching mathematics lessons in new ways, as well as support from a professional developer, before they can successfully teach lessons in ways that align with the goals of the professional development (Polly & Hannafin, 2011; Polly, 2011b).
Future LCPD mathematics programs should continue to include classroom-embedded professional development activities that have been carefully thought out and align well to the goals of the project and the workshop activities. Research on the impact of these activities could be examined using iterations of the same professional development project with some teachers working on classroom-embedded activities and workshops, while others only participate in workshops. Preliminary findings from a study focused on mathematics formative assessment indicates that the presence of classroom-embedded activities was associated with a higher fidelity of implementation of the emphasized pedagogies (Author, in press).
Addressing Aspects of the MKT Framework
The MKT framework provides a more specific description of the knowledge that teachers draw on when teaching mathematics. The present study was designed based on LCPD Principles to address all of the aspects of the MKT framework, with a focus on the aspects related to Pedagogical Content Knowledge, specifically Knowledge of Teaching and Content, Knowledge of Students, and Knowledge of Curriculum. The project also addressed teachers’ knowledge of content.
Based on the workshop feedback, teachers reported learning a great deal about the aspects of MKT on the right side of the diagram (Figure 2). Teachers reported deepening their understanding of the Common Core Mathematics Standards (Knowledge of Curriculum), planning mathematics lessons (Knowledge of Teaching and Content) and strategies to teach content (Knowledge of Teaching and Content and Knowledge of Students). The LCPD approach in this project actively put teachers in situations to deepen their knowledge of content and pedagogy. Teachers spent the workshops busily solving tasks, analyzing strategies, and examining their grade-level standards. The most negative pushback from teachers was after Workshop One when some reported not seeing a clear connection to solving mathematical tasks that were not related to content that they were currently teaching or directly aligned to their grade level (Mathematics on the Horizon). Teachers also reported some skepticism, but not overtly negative comments about teaching mathematics in the new format of starting with a cognitively-demanding mathematical task (Knowledge of Teaching and Content) and assessing students during teaching (Knowledge of Students).
Teachers’ feedback related to exploring mathematical tasks improved during Workshop Two and Workshop Three. With the group of teacher-participants it is unknown if a longer duration of professional development or more experiences planning lessons in this new format or working on formative assessment would lead to more positive, less skeptical reports about planning and assessing. Prior studies have cited that more ongoing, comprehensive learning experiences with opportunities to reflect on their own practice lead to higher enactment of pedagogies (Author, 2011, 2013; Fishman, et al., 2003; Wei, et al., 2009).
Future studies should further explicate the influence of specific aspects of the MKT framework during professional development on teachers’ reactions, their instruction, and their students’ learning. For example, if professional development programs focused only on the right side of the diagram, the side related to Pedagogical Content Knowledge and intentionally did not address mathematics on the horizon or specialized content knowledge what would the impact be?
Professional development continues to be heralded as a vehicle to greatly improve teachers’ instruction and their students’ learning. In this current age of high-stakes assessment and accountability there is a need to examine what components of professional development are likely to lead to higher enactments of research-based pedagogies and gains in student learning. This present study examined the influence of a learner-centered professional development (LCPD) program that was designed to address aspects of the Mathematical Knowledge for Teaching (MKT) framework.
While the study was limited to teachers’ report of what they learned as well as notes from conversations between the professional developer (author) and district leaders, the findings provide valuable information about what teachers focused their learning on- the exploration of mathematical tasks, the planning of mathematics lessons using a new format, and strategies to teach specific mathematics concepts. Teachers also reported gaining knowledge related to assessment, but many did not report knowing enough to actually enact those pedagogies in their classroom.
This research was previously published in the Handbook of Research on Professional Development for Quality Teaching and Learning edited by Teresa Petty, Amy Good, and S. Michael Putman, pages 62-84, copyright year 2016 by Information Science Reference (an imprint of IGI Global).
Alexander, P. A., & Murphy, P. K. (1998). The research base for APA's learner-centered psychological principles . In Lambert, N. M., & McCombs, B. L. (Eds.), Issues in school reform: A sampler of psychological perspectives on learner-centered schools (pp. 33–60). Washington, DC: American Psychological Association. doi:10.1037/10258-001
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special. Journal of Teacher Education , 59(5), 389–407. doi:10.1177/0022487108324554
Banilower, E. R., Boyd, S. E., Pasley, J. D., & Weiss, I. R. (2006). Lessons from a decade of mathematics and science reform: Capstone report for the local systemic change through teacher enhancement initiative . Chapel Hill, NC: Horizon Research, Inc.
Borko, H. (2004). Professional development and teacher learning: Mapping the terrain. Educational Researcher , 33(8), 3–15. doi:10.3102/0013189X033008003
Carpenter, T., Fennema, E., & Franke, M. L. (1996). Cognitively guided instruction: A knowledge base for reform in primary mathematics instruction. The Elementary School Journal , 97(1), 3–20. doi:10.1086/461846
Coffey, A. J., & Atkinson, P. A. (1996). Making Sense of Qualitative Data: Complimentary Research Strategies . Thousand Oaks, CA: Sage.
Common Core State Schools Initiative. (2011). Common Core State Standards- Mathematics. Retrieved from http://www.corestandards.org/
Fennema, L., Carpenter, T., Franke, M., Levi, M., Jacobs, V., & Empson, S. (1996). A longitudinal study of learning to use children's thinking in mathematics instruction. Journal for Research in Mathematics Education , 27(4), 403–434. doi:10.2307/749875
Fishman, B. J., Marx, R. W., Best, S., & Tal, R. T. (2003). Linking teachers and student learning to improve professional development in systemic reform. Teaching and Teacher Education , 19(6), 643–658. doi:10.1016/S0742-051X(03)00059-3
Garet, M., Porter, A., Desimone, L., Briman, B., & Yoon, K. (2001). What makes professional development effective? Analysis of a national sample of teachers. American Educational Research Journal , 38(4), 915–945. doi:10.3102/00028312038004915
Glazer, E. M., Hannafin, M. J., Polly, D., & Rich, P. (2009). Factors and interactions influencing technology integration during situated professional development in an elementary school. Computers in the Schools , 26(1), 21–39. doi:10.1080/07380560802688257
Hawley, W. D., & Valli, L. (2000). Learner-centered professional development. Research Bulletin, No. 27 . Phi Delta Kappa Center for Evaluation, Development, and Research.
Heck, D. J., Banilower, E. R., Weiss, I. R., & Rosenberg, S. L. (2008). Studying the effects of professional development: The case of the NSF's local systemic change through teacher enhancement initiative. Journal for Research in Mathematics Education , 39(2), 113–152.
Hill, H. C., & Ball, D. L. (2004). Learning mathematics for teaching: Results from California’s mathematics professional development institutes. Journal for Research in Mathematics Education , 35(5), 330–351. doi:10.2307/30034819
Loucks-Horsley, S., Stiles, K. E., Mundry, S., Love, N., & Hewson, P. W. (2010). Designing professional development for teachers of science and mathematics (3rd ed.). Thousand Oaks, CA: Corwin Press.
McGee, J. R., Wang, C., & Polly, D. (2013). Guiding teachers in the use of a standards-based mathematics curriculum: Perceptions and subsequent instructional practices after an intensive professional development program. School Science and Mathematics , 113(1), 16–28. doi:10.1111/j.1949-8594.2012.00172.x
National Council for Teachers of Mathematics. (2014). Principles to Action: Ensuring Mathematical Success for All . Reston, VA: Author.
National Partnership for Excellence and Accountability in Teaching (NPEAT). (2000a). Improving professional development: Research based standards . Washington, DC: Author.
National Partnership for Excellence and Accountability in Teaching (NPEAT). (2000b). Revisioning professional development: What learner-centered professional development looks like . Oxford, OH: Author.
Polly, D. (2011a). Examining teachers’ enactment of TPACK in their mathematics teaching. The International Journal for Technology in Mathematics Education , 18(2), 83–96.
Polly, D. (2011b). Examining teachers’ enactment of technological pedagogical and content knowledge (TPACK) in their mathematics teaching after technology integration professional development. Journal of Computers in Mathematics and Science Teaching , 30(1), 37–59.
Polly, D., & Hannafin, M. J. (2010). Reexamining technology’s role in learner-centered professional development. Educational Technology Research and Development , 58(5), 557–571. doi:10.1007/s11423-009-9146-5
Polly, D., & Hannafin, M. J. (2011). Examining how learner-centered professional development influences teachers’ espoused and enacted practices. The Journal of Educational Research , 104(2), 120–130. doi:10.1080/00220671003636737
Polly, D., McGee, J. R., Wang, C., Lambert, R. G., Pugalee, D. K., & Johnson, S. (2013). The association between teachers' beliefs, enacted practices, and student learning in mathematics. The Mathematics Educator , 22(2), 11–30.
Polly, D., Neale, H., & Pugalee, D. K. (2014). How does ongoing task-focused mathematics professional development influence elementary school teacher's knowledge, beliefs and enacted pedagogies? Early Childhood Education Journal , 42(1), 1–10. doi:10.1007/s10643-013-0585-6
Shulman, L. S. (1987). Knowledge and teaching: Foundation of the new reform. Harvard Educational Review , 57(1), 1–23. doi:10.17763/haer.57.1.j463w79r56455411
Smith, M. S., Bill, V., & Hughes, E. K. (2008). Thinking through a lessons: Successfully implementing high-level tasks . Mathematics Teaching in the Middle School , 14(3), 132–138.
Smith, M. S., & Stein, M. K. (1998). Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School , 3(7), 344–350.
Stanford University. (2015). You Cubed. Retrieved from: http://www.youcubed.org
Thames, M. H., & Ball, D. L. (2010). What math knowledge does teaching require? Teaching Children Mathematics , 17(4), 220–225.
Wang, C., Polly, D., Lehew, A., Pugalee, D., Lambert, R., & Martin, C. S. (2013). Supporting teachers' enactment of elementary school student-centered mathematics pedagogies: The evaluation of a curriculum-focused professional development program. New Waves - Educational . Research for Development , 16(1), 76–91.
Wei, R. C., Darling-Hammond, L., Andree, A., Richardson, N., & Orphanos, S. (2009). Professional learning in the learning profession: A status report on teacher development in the United States and abroad . Dallas, TX: National Staff Development Council.
Work, A. P. A. Group of the Board of Educational Affairs (1997). Learner-centered psychological principles: A framework for school reform and redesign. Washington, DC: Author.
Classroom: Based Professional Development: Professional learning opportunities for teachers that are based on activities that they complete in their classroom with students.
Common Core State Standards for Mathematics: A set of standards sponsored by the National Governor’s Association and Chief Council of State School Officers, initially adopted by 46 states in the United States.
Learner-Centered Professional Development: Professional learning opportunities for teachers based on the APA learner-centered principles.
Mathematical Knowledge for Teaching: A construct denoting the various aspects of knowledge associated with teaching mathematics.
Mathematical Tasks: The problems or activities that learners engage with.