
The results shown in the following chapter come from a research that shows some of the transformations of the concept of linear function observed from its definition in mathematics when facing the written, intended and enacted curriculum. This study was developed in technological high school level, with the participation of three teachers of mathematics, who were teaching the course called Functions and Algebraic Thinking. A case study was considered as a practical research method to carry out the investigation, adopting various processes to gather evidence to describe, verify or create theory. Different sources of evidence were used to gather and analyze information, such as: the official program of the course, three textbooks, class recordings and the application of a questionnaire. The results show transformations in both, the concept of function and the concept of linear function, pointing out, in this way, an educational problem that should be solved by modifying not only the concept, but also the teaching and learning of it.
Within the mathematical community, the function is acknowledged as the most important concept and it is also accepted as a strand that goes through the curriculum from the basic levels to university level. The studies related to the curriculum take into account the following elements: the official, intended, implemented and achieved curriculum (Díaz, 2008).
Researches about the notion of function show its evolution from an intuitive emergence to a formal approach of the object. It might seem that as there is a progress in the accuracy of the mathematical concepts, as well as an encouragement to understand them. However, this has not been possible, since such formalization and use of efficient notation lacking the intuitive basis that give rise to the mathematical concepts results in difficulties to learn them. Such is the case of the concept of function.
In the literature the four definitions that appear more frequently in textbooks of mathematics of the 20th century are: function in terms of the variable, function in terms of set of ordered pairs, function in terms of rule of correspondence, and function in Logo environment (Hitt, 2002).
Research shows the existence of difficulties and wrong conceptions from the students when learning the concepts of function and linear function related to: what is and is not a function, linearity and non-linearity, correspondence, continuous vs. discrete graphs, representations of a function graph, reading and interpreting graphs, concept of variable, and notation.
However, if the concept of linear function has been widely studied from a cognitive perspective, it is also true that there are areas from which it has not been studied enough yet, for instance, the corresponding area to strengthen the studies that come from the curriculum and focus on the teaching practice placed in a specific mathematical object.
Due to the opportunity mentioned above, throughout this chapter the following question arises: Which are the transformations of the concept of linear function noticed from its mathematical definition when facing the written, intended and enacted curriculum, in Mexican technological high schools during the second semester of the course called Functions and Algebraic Thinking?
This report includes the problem, literature review, theoretical framework, methodology, results, discussion, recommendations, future research directions, conclusion, and references that support this research. Regarding the results, it was found that there is an educational problem about the concepts of function and linear function and that due to its importance, it is necessary to take up the challenge of changing the vision and action about its concept, teaching and learning.
The study of the concept of function in the teaching of mathematics in high schools plays an important role in students’ learning, not only for the fact of being related to topics of different subjects, but also for the fact that it allows to represent real situations (Hitt, 2002). The different difficulties that arise when there are new studies related to the concept of function or to a type of function must also be emphasized.
Diaz (2008) notes that the curricular aspect of the concept of function is a kind of strand that goes from the basic education to university. He also warns about the difficulties the students face to understand this concept, as well as how this concept has generated a growing body of researches, like the ones that study the problem of teaching, the difficulties of learning, those that propose theoretical frameworks or even those that are focused on the diversity of interpretations of the concept of function.
There are several authors that have been devoted to work on the concept of function. During the 1980s, Leinhardt, Zaslavsky and Stein (1990) made a bibliographic revision, in which they showed the difficulties that students face when they try to conceptualize the idea of function, emphasizing issues related to the function such as rule of correspondence as well as its different representations, its reading and interpretation. On the other side, in the research done by Birgin (2012), linear functions are seen as a complex idea of multiple faces whose power and richness cover almost all of the mathematical areas. It is important to add that due to its several applications in the real world some topics of more advanced level, like those that come from calculus, can be reinforced.
It is true that the concept of linear function has been deeply studied from a cognitive approach, as evidenced by Díaz (2008), and it is also true that there are areas from which this concept has not been explored, for instance, the one corresponding to strengthen the studies coming from the curriculum and focused on a specific mathematical object. Such is the case of this research, interested in showing the transformations of the linear function observed in the written, intended and enacted curriculum, which will be analyzed through the performance of three teachers of mathematics of Mexican technological high schools in the course called Functions and Algebraic Thinking.
Thus, the following issue arises: What are the transformations of the concept of linear function observed from its mathematical definition when facing the written, intended and enacted curriculum?
All this involves the ability to identify transformations and/or modifications, first of people who plan the official school program and then, teachers who use and understand the information of the school program to design the activities that will be planned and done in the classroom.
The study is set within the technological high school level, because this level of education gathers the knowledge coming from the basic levels with the knowledge in the university, and the course that was taken into account was Functions and Algebraic Thinking, taught in the second semester of the corresponding school programs.
In this section some studies that have arisen in relation to the linear function will be described.
Historical Studies
Among the historical studies, the one raised by Acosta (2011) stands out, where he indicates that linearity through its meanings, as well as its predecessor, proportionality, are concepts that have evolved over history and arise from everyday needs of the time and culture, from the 19th century, to form a body of structured knowledge into formal theories. He specifies that the evolution of these ideas can provide elements resulting in the didactic installation of the concept of linearity in which students study them at different moments of their school career. He also affirms that didactics of mathematics has not included the elements that connect the concepts of linearity found in mathematics topic and, much less, found in courses. He adds that it is not unusual that within teaching aids, linearity is connected to everyday experiences, to any continuous phenomenon, whose behavior is represented in a graphic as a straight line. In this way, the school discourse found in textbooks supporting teaching as well as in explanations given by a teacher in class usually comes from common experiences to explain a linear phenomenon.
Cognitive Studies
As pointed out before, Leinhardt, et al. (1990) did an extensive research during the 1980s and identified that students face serious problems regarding several aspects, such as correspondence and linearity. Two types of difficulties were reported regarding the learners’ understanding about the permissible types of correspondence that are part of the functions. The first one is related to the belief that functions should personify a one-to-one correspondence, and the second is related to the confusion between the many-to-one and one-to-many correspondences. It is acknowledged that several studies have emphasized the learners’ tendency to gravitate towards linearity in a variety of situations, for instance, Lovell (1971, as cited in Leinhardt, et al., 1990) found that students had a strong tendency to define a function as a relation that produced a straight line pattern in a graph.
On the other hand, Chiu, Kessel, Moschkovich and Muñoz-Núñez (2001) carried out a case study in which they showed the way associated concepts and strategies of two different students arose and changed during a course of six tutoring sessions, especially designed to develop the concept of linear function. Posada and Villa-Ochoa (2006) developed a proposal to introduce the concept of linear function from a variational approach, where they reviewed the concept of significant unit introduced by Duval (1999) to determine some characteristics of the linear function. Regarding the concept of linear function, they determined the significant units from the variation and rate of change, since it is the constant rate of change the one that allows to determine the concept of linear function from a variational point of view. Meanwhile, Birgin (2012) showed in his study that students face difficulties to understand linear function, as well as to develop its concept, to move between its representations, and especially, that they do not identify the whole structure of the concept.
Regarding proportionality, it is important to review the work of Fandiño (2005), as well as of Brousseau, Brousseau and Warfield (2004, 2008 and 2009).
Curriculum Studies
In the research developed by Lloyd and Wilson (1998), they present the ideas linked to the impact of the teachers’ concepts regarding functions and their implementation in a curricular reform. In his study, Gilbert (2003) presents an experience of professional development related to an analysis of case studies based on a video made for mathematics teachers of middle school about linear functions. Chávez, Grouws, Tarr, Ross and McNaught (2009) show some findings related to the mathematics teachers of middle school regarding the use of teaching materials, making specific reference to the content of linear function.
The presence of a professional area devoted to the study of didactic phenomena related to the teaching and learning of mathematics at schools such as the educational mathematics has allowed researchers and teachers to focus on the curriculum (Rico, 1998).
It is also known that since the 1960s there is a special interest in the concept of curriculum, especially in the educational mathematics as stated by Rico (1998). In the same way, as Kilpatrick (1992) mentions, comparative and large scale studies stand out in relation to longitudinal studies. Moreover, in the Symposium held in Osnabrück in 1980, it was well known that during the 1970s, the professionals on educational mathematics had learned to revise the concepts about the meaning of curriculum by accepting the difference between intended, implemented and attained curriculum.
Burkhardt (2014) recognizes that the term curriculum is used with different meanings with the potential to widen such idea to any part of the world. Thus, while for some people the concept of curriculum refers to textbooks, for others is related to a set of experiences acquired by children in the classroom.
The model proposed by Stein, Remillard and Smith (2007) considers four elements of the curriculum, presented below:
The review of other proposed models for the study of curriculum, such as Flanders (1994), Schmidt et al. (1997), Stein, et al. (2007), Hirsch and Reys (2009), Mesa, Gomez and Cheach (2013) and Remillard and Heck (2014) allowed to consider a model that considers four components and one of them is the textbook, which is indicated in Figure 1.
| Figure 1. Elements considered in each component of the proposed model of curriculum |
|---|
 |
It is also important to pay special attention to external elements that arise when comparing the components, such as the teacher’s beliefs and knowledge as well as their professional identity, among others as noted by Stein, et al. (2007).
This research is intended to identify, describe and analyze the transformations of the linear function noticed from its mathematical definition to confront the written, intended and enacted curriculum by considering three mathematics teachers of a Mexican technological high school trough the course called Functions and Algebraic Thinking.
To develop this work of investigation, the research method called case study was used, which according to Eisenhart (1989) is a strategy of investigation to understand the dynamics found in very specific contexts, adopting several methods to gather evidence in order to describe, verify or create a theory. Moreover, Yin (1989) states that the case study consists of a detailed description and analysis of social units or educational institutions. For this reason, the case study is understood as a strategy that allows getting deeper into the social unit in order to emphasize and understand some specifications. This social unit can be made by one or more individuals or even by institutions such as a school.
Taking into account what Yin (2009 as cited in Cohen, Manion & Morrison, 2011) explains that there are various resources that allow gathering information for the study, including documents, interviews, files, physical objects like photos, direct and participant observation, which allows getting deeper in the development of the research without focusing only on one resource of evidence.
This study was developed in five stages according to the model proposed in Figure 2.
| Figure 2. Elements considered in each component of the proposed model of curriculum |
|---|
 |
The research included the following stages:
Participants
There were three teachers involved in this research: Lulu, Iris and Israel, with 12, 18 and 14 years of teaching experience, respectively. It is important to clarify that the names of the involved teachers of this study are not real; they have been changed to protect their identities and assure their confidentiality. The academic education of each teacher is the following one: teacher Lulu graduated from a Normal School where she was trained as a mathematics teacher; teacher Iris studied architecture and graduated from the Autonomous University of the State of Mexico, and teacher Israel has a degree from a Center for Updating Teachers.
Instruments
A questionnaire was used to gather specific information about the three teachers; it includes their place of work, the subjects they teach, years of service, the number of groups they teach and information about their professional training (see Appendix). Two tables were used to analyze the transcriptions of the teachers’ classes that were observed, one table related to the different representations of the concept of function and another one related to the components of the linear function.
To develop the data analysis, Table 1 and Table 2 summarize the ideas proposed by Cantoral (n.d), Hitt (2002) and Larson and Hostetler (2001).
Table 1. Different ways to represent a function
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Representations of a linear function | Black box: an input/output model | Special case of relation | Correspondence between sets | Table of values | Ordered pairs | Graph | Relation between variables | Formula | Model | Construction of a functional equation |
Table 2. Main components of a linear function
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Elements of a linear function | Domain | Codomain or target set | Image or range | Rule of correspondence | Cartesian Plane | Slope |
Value of the origin ordinate |
Monotony (increasing or decreasing) | Concept of linear function | Concept of constant function |
This section describes the results obtained about the transformations of the concept of linear function in the classes given by the three high school teachers. These transformations are explored through a comparison between what the school program anticipated, what the teachers planned and what happened in the classroom, as well as what mathematics states as concept of linear function.
In relation to the written curriculum, the official program proposes implicitly the use of the representations that the teacher could use when working with the concepts of function and linear function. These representations could be verbal, algebraic, equation, graph and table representations. Education authorities do not offer official textbooks.
In relation to the intended curriculum and textbooks, Table 3 presents the elements considered when studying the notions of function and linear function in textbooks.
Table 3. Concepts of function and linear function proposed in the textbooks
| Concept of Function | Concept of Linear Function |
|---|---|
| Eslava (2012) | |
| A function is a relation in which each element of the domain has one and only element of the codomain, thus, every function is a relation, but some relations are not functions. (Eslava, 2012, p. 48) | The canonical or usual form of a linear function or first-degree polynomial function is Its domain and range are real numbers. The graphic of If If If The independent concept |
| Orozco (2013) | |
| A function is a relation in which each element from the first set |
Its correspondence rule is a polynomial of degree one or zero; its graphic is always a vertical line, as follows: Analysis of the linear function Case 1: Case 2: Case 3: Case 4: (Orozco, 2013, p.p. 128-131) |
| Mendoza (2014) | |
| “A function relation or function is a relation between two set, in such a way that it associates each element of the domain to only one value of the codomain, so it is also a rule of correspondence. It is important to mention and understand that every function is a relation, but not all relations are functions.” (Mendoza, 2014, p. 41) |
One of the main applications of the linear functions is in direct variation problems A linear function is when its image is a vertical line and its general form is: Where: (Mendoza, 2014, p. 58) |
It should be noted that in three reviewed textbooks, teachers were provided with a limited view of the formal definition of the concept of function. It is expected to give a set-theoretic and static definition of the concept of function. Regarding the concept of linear function, the texts of Eslava (2012) and Orozco (2013) show a set-theoretic definition of the concept, while the textbook of Mendoza shows a variational approach.
In the texts of Eslava (2012) and Orozco (2013) the function is considered as a polynomial, in the first case a first degree polynomial and in the second case a first or zero degree polynomial. Regarding Eslava’s (2012) text, there is an internal contradiction in relation to considering a constant function as a linear one.
Due to these types of presentations of the concept of linear function from Eslava (2012) and Orozco (2013), a trend towards the concept of family functions is noticed, while in Mendoza’s text (2014), the concept of linear function, applied in direct variation problems, as well as the concept of rate of change, leads to confusions regarding considering a coordinate, “the ordinate to the origin” as a point of the plane; “
is the intersection between the slope and the ordinates”.
Now as far as the transcriptions of the classes observed, the following issues were found. In the introduction of the concept of linear function, the teachers used notions about the concept of function, as shown in Table 1, and characterized as: special case of relation, correspondence between sets, table of values, ordered pairs, relation between variables, formula, model and functional equations. In other words, two approaches about their teaching methods coexisted: the dynamic and the static one, with greater emphasis on the first mentioned. Despite the above mentioned, the teachers only exposed conceptual images of the concept of function and linear function, understanding a conceptual image to be what helps describe a total cognitive structure associated with the concept, which includes all the mental images, as well as the processes and the associated properties, as it is determined by Tall and Vinner (1981). A conceptual image is built over the years by means of all kind of experiences and it changes as individuals face new stimuli.
As an example, it is suggested to see the following partial transcription of session 1 of one of the teacher’s talking about the notion of function, as shown in Table 4.
Note: In the following Transcription 1 of the class these codes were used:
Table 4. Partial transcription of session 1of one of the teachers observed when introducing the concept of linear function
| …. Fs: It is said, in mathematics, that a quantity is function of another one if the value of the first one depends only on the value of the second one. T: Ok, someone else? Fs: A function or […] refers to a rule given to each element of a first set, a unique element of a first set, and a unique element of the second set. O: The definition proposed by the student sounds weird and the teacher seems to realize this. T: Mmm… T: Could you read the last three lines again? T: Loudly. Fs: It refers to a rule given to each element of a first set, a unique element of a first set, and a unique element of the second set. T: Thank you. Over there (pointing to the students next to the door). Fs: But this one is quite similar. T: Someone with something different. Ms: It says: Algebraic functions. Ms: In the algebraic functions the operations to be solved with the independent variable are: addition, subtraction, multiplication, division, potentiation and radication. T: Let us see, this one (…) the one your classmate read is an algebraic function, but it is part of the concept of functions, and I want only the concept of a function. T: Let us see. You, tell me. O: She addresses to one of the students on the other side of the classroom, in the line in front of the desk. O: The student remains silent. Ms: She is asking you to tell her the concept of function! T: What is a function? Taking into account what your classmates just read. T: The teacher crosses her arms waiting for an answer. O: All his classmates turn around to see him. Ms: Function is (…) a quantity that depends (…) T: Here we have an example of a function, if you paid attention to what your classmates read, it says that there are two sets, a first set that we will call trades and professions, and a second set that we will called work items, then we associate one to one, which means that it is a function. ... |
Regarding the way of dealing with linear function, the teachers taught it in a “sequential” way, by following a scheme of algebraic representation to a tabular representation, and then a graphic representation, with little presence of the reverse process. In other words, to find the algebraic representation for a given graphic of a linear function as shown in Table 5. Note the following Transcription 2 related to the above mentioned.
Table 5. Partial transcription of session 2 of one of the teachers talking about the concept of linear function
| … T: Among all these functions, this one belongs to a linear function [pointing to the following: T: It has the form of T: I have realized that when I give you a function and tell you that is a linear one, some of you say: “It is going to be a straight line”. I hope you always identify it, ok? Since it is usually one of the questions in the “Enlace” exam, “PISA” exam, entrance exams or knowledge tests to be hired in a company. T: How am I going to graph it if I am only given the function? T: I am going to assign value for T: That is right, and I am going to make a substitution where I have the value and then I am going to the get the value of P: I will get an ordered pair O: Figure 3 shows what has been done by the teacher. T: There are two types of variables: dependent and independent variable. T: T: Why is it called independent variable? Because I can assign it any value I want. I can consider a wide range of values. T: Since I locate my coordinate plane, although I may also locate only some of them. T: What characteristics should I consider? [She asks the students]. T: The fact of having the same space between each division, ok? And the fact of having the same scales T: Here, I can use 1,2,3,4,5,6,7,8,9 and [referring to the T: Yes? What is not correct, would be if I put 1, and then 20, and then 100, not in this way. I have to use the same scale. T: In this case, I am going to consider the following values [from -3 to 3]. T: Now, what I am going to do is to substitute this independent variable in this function. O: Figure 4 shows what has been done by the teacher. O: A student noticed that the teacher had not located the negative numbers within the domain, which is why the positive numbers appear first in the domain, and then the negative ones. T: Then, my ordered pair will be O: A student raises his hand to ask a question. Ms: Are we going to have in all the values of T: Yes, I did, just to follow the conventional roles. You can use the same ones, or you can use any other values. |
| Figure 3. A table made by the teacher to start tabulating the linear function |
|---|
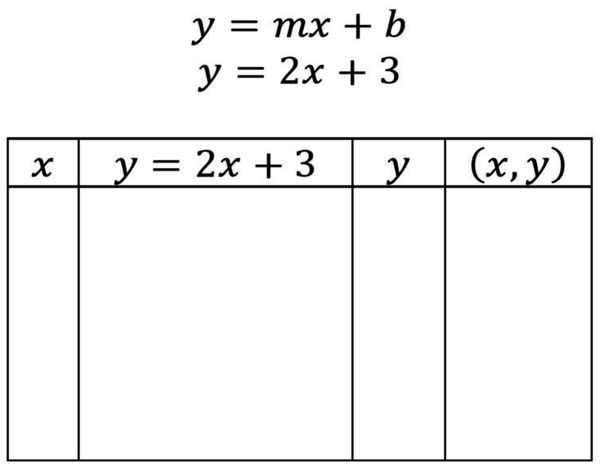 |
| Figure 4. The table shows the first coordinate obtained by the teacher |
|---|
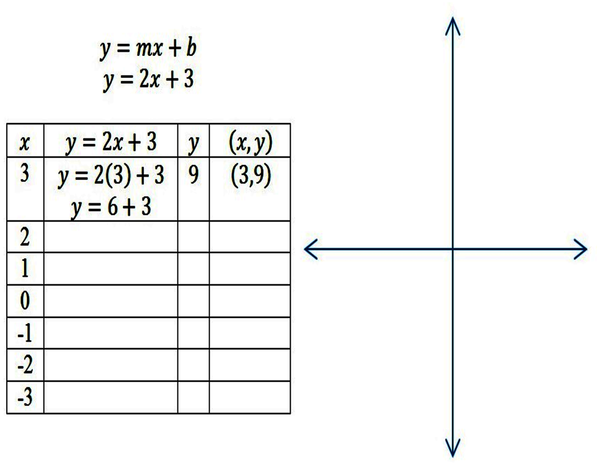 |
Some difficulties faced by the teachers when they move in between representations are noticed. Through the development of the tables and the language used by the corresponding teacher, the understanding of the domain of the linear function as rational numbers instead of real numbers is evident. The following Transcription 3 shows in Table 6 what one of the teacher’s presented to the students.
Table 6. Partial transcription of session 2 of one of the teachers talking about the domain and codomain of a function
| … T: No? Let us see, guys, then, is the domain of this function only this set? O: The teacher points to the initial domain used in the tabulation. Ss: No. P: No, right? Which would be the domain of this function? Ms It would be infinite. T: Mm! Your classmate says it would be from infinite to minus infinite and, which is this set? Which set of numbers? Ms: Natural numbers. T: The natural ones? Fs: No! T: Which set of numbers? O: Students remain silent. T: Remember that we learned that natural numbers are from zero to infinity, then, you are just mentioning the ones here.[while she points to the positive side of the T: Then, which is the set of the domain? Ms: Wholes. T: Wholes? T: Wholes are another set of numbers that go from minus infinity to plus infinity, right? O: While she asks the questions, she marks on the whiteboard each set and the way each one includes another one. T: But, let us see [she goes back to the table of values]. T: Can I assign the value here of Ms: Yes. T: Yes? Which set does it belong to? Fs: To the rational ones. T: To the rational ones. Then, I included another one, the rational ones, which are those that are giving a ratio, of T: But all these belong to another one, which ones? Ms: Eh, mmm. T: What is the set that includes all of them and mentions them? Which one? Ms: The irrational ones. O: The teacher shakes her head to indicate a negative answer. T: The real ones. Real numbers are those that include the natural, whole and rational numbers. T: Then, which is its domain? T: The real ones, all the real numbers. Good. … |
By observing the algebraic processing of the linear function, it is evident that there is a parametric approach, by assigning values to (slope) and to
(intercept) in the expression
, and getting families of straight lines. This fact was intended to be spread through the use of a chart builder called “Graphmatica”. In spite of the above, the assigned values to
(the slope), are only positive values, excluding negative slope lines or zero. Table 7 illustrates the process developed by one of the teachers.
Table 7. Partial transcription of session 6 of one of the teacher exploring the slope
| … T: A quarter. Look, because remember that it is only a few seconds and it appears immediately. T: Ready? Look. T: Which one is it going to appear? T: The one of T: Did you see it? Ss: No. T: It is not possible to see it. T: So, I will change the color. Ms: Where is it? T: It is the blue one… O: As it is not possible to see the blue color, then the teacher changes the color of the graphic. T: Under the red one, there is a lilac or purple one. Ok? O: A student immediately points so as the rest of his classmates could see it, as it is shown in the Figure 5. T: Now, what can you tell me about these graphs? T: What is your conclusion? O: A student mentions something about a coordinate (it is not possible to listen to her, because all the students talk at the same time) T: Which coordinate? How is it called? Help her. Ms: Coordinates? Fs: It is the slope, is it not? T: The lower the slope… Fs: The greater will be… T: It is steeper, right? T: It is close to… how many degrees if the slope is greater? … It is close to… Ms: 90? P: 90, and how do I know it? Ms: Yes, because ninety degrees… O: The student represents how a 90 degrees line looks like. T: Yes, yes, that is right. Your classmate says: ninety degrees. |
| Figure 5. A student pointing to the graphic representation of |
|---|
 |
There is also evidence of the representation of the linear function as a model, through different approaches or the use of real life phenomena: problem of speed in uniform rectilinear motion, and some others; however, it is also evident that there are serious difficulties in teaching it. Regarding the above mentioned, the selected excerpt in the following Transcription 5, that is shown in Table 8 illustrates the part of the situation that has emerged and the problems that were found.
Table 8. Partial transcription of session 4 of one of the teachers talking about linear function as a model
| … T: What is the velocity function? O: Another team shows the teacher their answer to question one. T: Very close, very close… but this is not the formula. T: You got it, but here it is indicating you that it is about velocity. O: What students do not remember is how to calculate velocity, so the teacher makes an effort to help them remember, so they can get the function with the information they already have. She ends up by telling them that velocity equals distance divided by time. O: The teacher moves over to another team. … T: Is it ready, guys? T: Let us see. Let us check it, ok? O: The teacher starts erasing the information on the whiteboard, draws a Table 9 of values as shown below: |
Table 9. This table was done by the teacher on the whiteboard
T: Ready? T: Let us see. T: What difficulties do we find? Let us see, tell me. T: Let us see. How is it related to another area of knowledge? T: Which area is it related? Ms: With… uhm…physics…it could be. T: With the subject of physics. T: Is this a real problem? Ss: Yes. [Only some of them answer. The rest keeps working on the answers] T: Yes, it is. It is a real problem. T: Like when we are in training, like the kind of training Ana Guevara used to have. She had to beat her own time through the meters she used to run. T: Good. …. |
There are several definitions for the concept of function, as a result of the evolution of the concept; some of them are dynamic and others static. Furthermore, there are four of the most common and well-known definitions that have been part of the textbooks during the 20th century.
To this respect, Hitt (2002, p.74) mentions that “the concept of set-theoretic notation, not only gave greater formality to the definition of function, but also favored a static approach about an intuitive idea of variation”.
However, as it was observed in the results, the concepts of function and linear function, despite being suggested as part of the official program of the technological high schools, are not explained, resulting in a great variety of possibilities to deal with them.
Regarding the revised texts used by the teachers during the observed and discussed sessions, only outlines of the formal definition are shown, for instance, for the concept of function, see the one exposed in Cárdenas, Lluis, Raggi and Tomás (2004, p.21) and in relation to function exposed in Spivak (1999, p.73).
Let and
be sets. A function
is a relation
in
that satisfies.
in other words, for each
there is a set
Each element is associated to only one of
or,
y
involves
An alternative notation for a function is is
Set is called domain of the function, set
is called the co-domain of the function, and for every
,
indicates the element of
corresponding to it, in other words,
. The
is the image of the element
.
Regarding the notion of linear function exposed by Spivak (1999, p.76) […] the graphic of the function is a straight line slope
that crosses the point
. For this reason, functions are called linear functions, which is illustrated in Figure 6.
| Figure 6. Graphic representation of linear function taken from Spivak (1999, p. 76) |
|---|
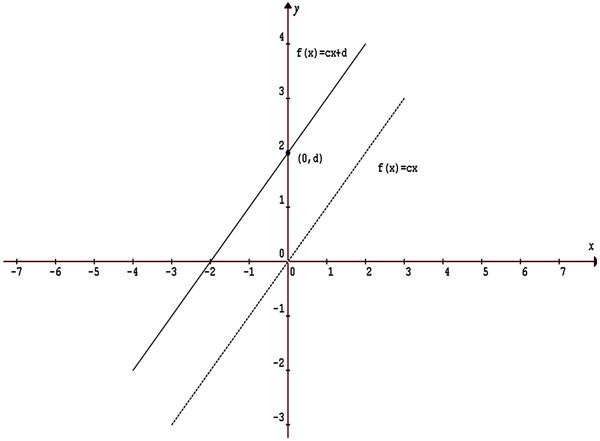 |
However, with regard to the evidence about the way teachers deal with the concepts of function and linear function, the procedures followed by them have a dual nature. In other words, these procedures are both intuitive and formal, with more emphasis on written practice or exercises using pencil and paper (such as numerical calculations, substitutions, tables, location of points in a coordinate system and graphs), with tendency to the induction of families of linear functions (parallel lines, converging lines in the origin). All these are considered as an early development of what is known as graphic language in the educational mathematics community. Procedures not in accordance with the stated by Leinhardt, et al. (1990, p.49): “In general terms, there is significant agreement on the fact that instruction should move from less formal, less abstract, more global and intuitive to the strict formal system”, are an accepted fact in the new curriculum proposal for the compulsory education in 2016 in technological high schools proposed in Mexico by the Secretariat of Public Education (SEP- according to its acronym in Spanish).
There are two types of transformations observed regarding the concept of function:
There are three types of transformations observed regarding the concept of linear function:
To determine and explain, for the technological high school level, the most appropriate way to develop the concept of function, that according to theorists in mathematics education could be the following one: the one related to the variable proposed by Hitt (2002), that considers the most appropriate one for this level the development of an intuitive idea of variation, and provides the following definition: A function associates an independent variable with a dependent one, so each value of the first one has one and only one value of the second one (p.76).
The study made it clear that it is possible continue the development of research including curriculum studies: Specifically, to carry out systematic support of teachers’ activities, under the premise of reflexive thoughts about their own teaching practice, as well as designing and building activities that involve different ways of presenting and approaching linear function. Similar studies can be developed to expand the material presented in this chapter.
Some of the findings from the research were that the official school program of the subject “Functions and Algebraic Thinking” suggests implicitly the use of only five representations to work the concept of function in their activities, which are: verbal, table, algebraic, graphical and equation, which correspond to the dynamic approach proposed by Hitt (2002). Meanwhile, the theoretical review found at least ten different representations to present the general concept of function. On the other hand, regarding the elements that teachers have to approach when developing contents, the properties or characteristics that they need to highlight are not clear as you can see in the official school program of the course.
The representations suggested by Larson and Hostetler (2001), as well as the ones suggested in Cantoral (n.d.) and Hitt (2002) appear in the recordings of the teachers’ lessons. One of the representations they do not use is the one of the function as a black box: the input/output model mostly used by teachers in basic teaching levels. Another representation used by professors Lulu and Israel was the correspondence rule, which is not included in the official program of the course, they added it.
The support materials used by teachers during their classes are textbooks, which have no official status. Teachers choose them freely, according to their expectations.
Fragments of the classes’ recordings demonstrated the following: Teachers tend to a stationary management of the linear function. They present difficulties in the conceptual construction of the real, when approaching the domain and codomain of functions. That is the case of teacher Lulu: in the recording of her lesson, she gives cause to state that the notion of ℜ for her is the set of rational numbers.
In summary:
This research was previously published in the Handbook of Research on Driving STEM Learning With Educational Technologies edited by María-Soledad Ramírez-Montoya, pages 238-259, copyright year 2017 by Information Science Reference (an imprint of IGI Global).
Acosta, J. (2011). La noción de linealidad. Una aproximación epistemológica, didáctica, cognitiva y sociocultural [The notion of linearity. Epistemological, didactic, cognitive and socio-cultural approach] (Unpublished doctoral dissertation). Research Center for Applied Science and Advanced Technology of the National Polytechnic Institute, México.
Birgin, O. (2012). Investigation of Eighth-Grade Students’Understanding of the Slope of the Linear Function. Boletim de EducaçãoMatemática, 26(42), 139-162. Retrieved from: http://www.redalyc.org/pdf/2912/291223573008.pdf
Brousseau, G., Brousseau, N., & Warfield, V. (2004). Rationals and decimals as required in the school curriculum. Part 1: Rational as measurement. The Journal of Mathematical Behavior , 23, 1–20. doi:doi:10.1016/j.jmathb.2003.12.001
Brousseau, G., Brousseau, N., & Warfield, V. (2008). Rationals and decimals as required in the school curriculum. Part 3. Rationals and decimals as linear functions. The Journal of Mathematical Behavior , 27(3), 153–176. doi:10.1016/j.jmathb.2008.07.006
Brousseau, G., Brousseau, N., & Warfield, V. (2009). Rationals and decimals as required in the school curriculum. Part 4. Problem solving, composed mappings and division. The Journal of Mathematical Behavior , 28(2-3), 79–118. doi:10.1016/j.jmathb.2009.08.002
Burkhardt, H. (2014). Curriculum design and systemic change . In Li, Y., & Lappan, G. (Eds.), Mathematics curriculum in school education (pp. 13–34). Dordrecht: Springer; doi:10.1007/978-94-007-7560-2_2
Cantoral, R. (n.d.). Cálculo. Un acercamiento didáctico y epistemológico. Ejemplar de presentación [Calculus. A Didactic and Epistemological Approach. Presentation Copy]. Iberoamérica.
Cárdenas, H., Lluis, E., Raggi, F., & Tomás, F. (1990). Álgebra superior [Advanced Algebra] (2ª ed.). Trillas.
Chávez, Ó., Grouws, D. A., Tarr, J. E., Ross, D. J., & McNaught, M. D. (2009). Mathematics Curriculum Implementation and Linear Functions in Secondary Mathematics: Results from the Comparing Options in Secondary Mathematics Project. San Diego, CA: American Education Research Association. Retrieved from http://cosmic.missouri.edu/aera09/ChavezGrouwsTarrRossMcNaught2009.pdf
Chiu, M. M., Kessel, C., Moschkovich, J., & Muñoz-Nuñez, A. (2001). Learning to graph linear functions: A case study of conceptual change. Cognition and Instruction , 19(2), 215–252. doi:10.1207/S1532690XCI1902_03
Cohen, L., Manion, L., & Morrison, K. (2011). Research methods in education . New York, NY: Routledge.
Diaz, J. L. (2008). El concepto de función. Investigaciones y enseñanza [The concept of function: Researches and Teaching]. In Rodríguez, E., Sosa, S., Luque, F., Robles, C., & Urrea, M. (Eds.), Memorias de la XVIII Semana Regional de Investigación y Docencia en Matemáticas 27 (pp. 35–40). Sonora: Mosaicos Matemáticos.
Duval, R. (1999). Semiosis y pensamiento humano. Registros semióticos y aprendizajes intelectuales [Semiosis and human thinking. Semiotic records and intellectual learnings]. Santiago de Cali: Universidad del Valle.
Eisenhardt, K. M. (1989). Building theories from case study research. Academy of Management Review , 14(4), 532–550.
Eslava, M. (2012). Pensamiento algebraico [Algebraic thinking]. Patria.
Fandiño Pinilla, M. I. (2005). Le frazioni, aspetti concettuali e didattici . Bologna, Italy: Pitagora.
Flanders, J. R. (1994). Textbooks, teachers, and the SIMS test. Journal for Research in Mathematics Education , 25(3), 260–278. doi:10.2307/749338
Flores, R. (2010). Significados asociados a la noción de fracción en la escuela secundaria [Meanings associated to the notion of fraction in secondary schools] (Unpublished Master's Thesis). Research Center for Applied Science and Advanced Technology of the National Polytechnic Institute, México.
Gilbert, M. (2003). A professional development experience: An analysis of video case-based studies for secondary math teachers in linear functions (Unpublished PhD Dissertation). University of Washington.
Hirsch, C., & Reys, B. (2009). Mathematics curriculum: A vehicle for school improvement. ZDM , 41(6), 749–761. doi:10.1007/s11858-009-0218-0
Hitt, F. (2002). Funciones en contexto [Functions in context]. Pearson Educación.
Kilpatrick, J. (1992). The history of research on mathematics education . In Grouws, D. (Ed.), Handbook of Research on MathematicsTeaching and Learning (pp. 3–38). New York: Macmillan.
Larson, R., & Hostetler, R. (2001). Precalculus . Houghton Miflin.
Leinhardt, G., Zaslavsky, O., & Stein, M. M. (1990). Functions, graphs, and graphing: Tasks, learning and teaching. Review of Educational Research , 60(1), 1–64. doi:10.3102/00346543060001001
Lloyd, G. W., & Wilson, M. (1998). Supporting innovation: The impact of a teachers conceptions of functions on his implementation of a reform curriculum. Journal for Research in Mathematics Education , 29(3), 248–274. doi:10.2307/749790
Lovell, K. (1971). Some aspects of growth of the concept of function . In Rosskopf, M. F., Steffe, L. P., & Taback, S. (Eds.), Piagetian Cognitive-Development Research and Mathematical Education (pp. 12–33). Reston, VA: NCTM.
Mendoza, J. (2014). Pensamiento algebraico [Algebraic thinking]. Grandes Ideas.
Mesa, V. M., Gómez, P., & Cheah, U. H. (2013). Influence of international studies of student achievement on mathematics teaching and learning. In K. C., C. Keitel, A. Bishop, F. Leung, & J. Kilpatrick (Eds.), Third International Handbook of Mathematics Education (pp. 861-900). Dordrecht: Kluwer. doi: doi:10.1007/978-1-4614-4684-2_27
Orozco, E. A. (2013). Pensamiento algebraico [Algebraic thinking]. Desde el Aula.
Posada, J., & Villa-Ochoa, J. A. (2006). Propuesta didáctica de aproximación al concepto de función lineal desde una perpectiva variacional [Didactic proposal of an approach to the concept of linear function from a variational perspective] (Unpublished Master's Thesis). Universidad de Antioquia, Medellín, Colombia.
Remillard, J.T., & Heck, D. J. (2014). Conceptualizing the curriculum enactment process in mathematics education. ZDM – The International Journal on Mathematics Education, 46(4), 705 – 718. doi: 10.1007/s11858-014-0600-4
Rico, L. (1998). Concepto de currículum desde la educación matemática [Concept of curriculum since mathematics education]. Revista de Estudios Curriculares, 1(4), 7-42. Retrieved from: http://funes.uniandes.edu.co/524/1/RicoL98-2713.PDF
Schmidt, W. H., McKnight, C. C., Valverde, G. A., Houang, R. T., & Wiley, D. E. (1997). Many visions, many aims: Vol. 1. Across-National Investigation of Curricular Intentions in School Mathematics . Kluwer Academic Publishers.
Spivak, M. (1999). Calculus (2nd ed.). Editorial Reverté.
Stein, M. K., Remillard, J. T., & Smith, M. S. (2007). How curriculum influences student learning . In Lester, F. K. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 319–369). Charlotte, NC: Information Age.
Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics , 12(2), 151–169. doi:10.1007/BF00305619
Yin, R. K. (1989). Case Study Research: Design and Methods . Newbury Park, CA: Sage.
Curriculum: The group of organized elements, with teaching purposes, that systematize the academic career of students.
Function: It is a rule that assigns each element of a first group a unique element of a second group. A function relates an independent variable to a dependent variable, so that to each value of the first, corresponds one single value of the second.
Lesson Recording: A tool used in research and the observation of facts, phenomena, processes and individuals, so as to demonstrate what was observed within a specific time and space.
Linear Function: Linear functions have the following form: , where
is the slope of the line and
is the length of the intersection with the y axis to the origin.
Mathematics Teacher: A professional that must have a thoughtful attitude regarding his own performance as a teacher.
Representation:: Any way or form in which an object, an idea or a concept is shown.
Teaching: It involves the interaction of three elements: the teacher, student and the object of knowledge.
Technological High School: An educational subsystem that corresponds to high school and offers a bivalent academic training.
Transformations: These refer to a change or modification of an idea, concept, figure or image.
Collection of the Teacher’s General Information