3
NATURE,
NURTURE, OR BOTH?

Can Heritability
Cut Psychology’s Gordian Knot?

What do baseball stars Barry Bonds (who set a new major-league record by hitting 73 home runs in one season), Cal Ripken, Jr. (who surpassed Lou Gehrig’s record of consecutive games played), Roberto Alomar, Sandy Alomar, Jr., and Ken Griffey, Jr., have in common? Each is the son of a former major league player or manager. Johann Sebastian Bach, one of the greatest composers in the history of Western music, was the father of Carl Philipp Emanuel, Johann Christian, Johann Christoph Friedrich, and Wilhelm Friedmann Bach, who also were composers, though none as illustrious as their father. Wolfgang Amadeus Mozart was the son of Leopold Mozart, also a composer, but not of his son’s caliber. And there are the Bernoullis in science and the Bolyais in mathematics, and the novelists Alexandre Dumas père et fils. Actress Drew Barrymore comes from a theatrical family that includes her grandfather John Barrymore and his sister Ethel, brother Lionel, and son John Drew Barrymore. And then there are the Fondas: Henry, Jane, Peter, and most recently, Bridget.

We all know there are “dynasties” in sports, music, science, and mathematics. The question is, why? Are genes for athletic, musical, or intellectual ability passed from parents to children, like those for hair color or blood type? Or are these abilities acquired, the way a child learns his or her parents’ language or religion? Or perhaps the genetically gifted children of genetically gifted parents are doubly endowed by being reared in home environments that foster their inborn talents?

Is it nature, or nurture, or both? That is psychology’s Gordian knot. Heritability is the sword that Jensen believes has cut the knot.

In this chapter we discuss the second of the three pillars of Jensenism—individual differences in IQ are more the result of the fact that we inherit different genes than of the fact that we grow up in different environments—and the political and scientific controversies that have swirled around it. In Jensen’s definition, “environment” encompasses every cause of individual or group differences that is not genetic. It includes biological factors (such as exposure to toxic chemicals, mother’s age and health, problems during childbirth, and even incompatibility in blood type between the mother and fetus) and quantifiable factors linked with socioeconomic status, or SES (such as family income, number of books in the home, and time spent by parents with their children) as well as qualitative cultural factors (such as growing up in a poor, Black, inner-city neighborhood versus an affluent, mostly White suburb).

Jensen does not deny that environment affects IQ. But, he says, not only are genes more important than environment, but the biological environmental factors are more powerful than cultural and socioeconomic factors. The average difference in IQ between siblings reared in the same household (where family SES and culture are pretty much the same) is greater than the average difference in IQ between families from different SES and cultural groups.

Contrary to the hopes and expectations that have shaped social policy since the days of the Great Society, genes play by far the biggest role in producing differences in IQ , followed by environmental differences (especially biological ones) between siblings who grow up in the same family. Differences in SES between families finish dead last. Therefore, even the most extreme government policy that made all families exactly equal in income, number of books in the home, quality of schools, time spent with parents—even providing professionals to assist disadvantaged parents in child rearing—could not eliminate or even substantially reduce IQ differences. Or so Jensen says.

Jensen supports his conclusions by citing studies of IQ that use the methods of quantitative genetics, especially a statistic called heritability.

Placing the case of Nature v. Nurture before the Court of Quantitative Genetics means that we must treat it like a civil suit, rather than a criminal case. For a specific criminal charge, say vehicular homicide, the defendant is found either 100 percent not guilty (and walks free) or 100 percent guilty. In civil suits such as auto accidents due to faulty original equipment or subsequent repair work, negligence can be apportioned. The judge can find each of the defendants 100 percent liable, 0 percent liable, or anywhere in between. For example, the judge may decide that the auto manufacturer is 60 percent liable and the repair shop 40 percent liable for the faulty brakes that caused the plaintiff ’s accident. Likewise, quantitative genetics renders its decision by apportioning the relative roles of genes and environment in producing individuals’ differences through a statistic called heritability.

For any measurable trait—height, the age at which teeth erupt, intelligence, or blood pressure—heritability is defined as the proportion of the total variance in the trait that is due to genes, and not to the environment (including the biological environment described earlier). We can even determine the heritability of traits like charisma or sex appeal, provided we can reliably and accurately rate individuals on those traits.

To understand heritability and the controversies that have swirled around it, it is necessary to understand just what that term does and does not mean. When Jensen states that the heritability of IQ in a particular group of people is 0.75, he is not saying that someone with an IQ of 100 got 75 IQ points from his genes and the remaining 25 from his environment. What he is saying is that 75 percent of the individual differences—the variation or the total variance in IQ—in that group is because of differences in their genes, and the remaining 25 percent of the total variance is due to differences in their environment (including the biological environment).

Quantitative genetics grew largely out of the work of Sir Ronald A. Fisher in which varieties of plants were grown in different types of soil and given different amounts of fertilizers or nutrients. Suppose that we are measuring differences in oil yield of genetically different corn seeds grown in the same soil and given the same amount of nutrients. Any significant differences that we find must be the result of genetic differences between the seeds. Conversely, differences between genetically identical seeds of corn grown in different soils or given different amounts of fertilizer must be the result of environmental differences. In the case of genetically diverse seeds grown in different soils and given different amounts of fertilizer, a heritability of 0.60 would mean that 60 percent of the measured differences in oil yield were the result of genetic differences between the seeds, and 40 percent of the differences were due to the different environments (soil and fertilizer) in which they were grown.

Jensen and other hereditarians applied this same reasoning to the study of differences in IQ and other human behaviors. Ethically, our society does not allow behavioral scientists to place children in different homes, give them different nourishment, or manipulate any other factor simply for research purposes. Nor would behavioral geneticists want to do so. Instead, they rely on “natural experiments” in which the resemblance in any trait between different degrees of kinship (that is, twins, siblings, unrelated children reared together) is compared with the degree of similarity predicted by genetic theory. By definition, however, these natural experiments lack the control of laboratory plant or animal studies.

One of the most informative natural experiments compared identical twins reared apart. Identical (also called monozygotic, or MZ) twins develop from a single egg fertilized by a single sperm that divides and then develops as two embryos. Sometimes the division is not complete and we get conjoined twins (commonly called “Siamese twins”). But in most cases, MZ twins are two (or more) genetically identical individuals—in effect, natural human clones. Just about everyone has known at least one pair of twins who look—and even act—alike. But again the question is why? Identical twins are often dressed alike by their parents and treated alike by others. To unravel the Gordian knot of nature versus nurture, we need to look at the rare cases of identical twins separated early in life (the earlier the better) and reared in different homes (the more different the better). These are often termed MZA (monozygotic twins reared apart) in human behavior genetic studies.

The correlation between the IQs of MZA twins (who inherited the same genes but were then reared in different environments) provides the best single estimate of the heritability of intelligence. The average correlation in IQ from the various studies of MZA twins is about 0.78. Working from the opposite direction, the fact that the correlations in IQ between parents and their adopted children (about 0.19) and between adopted children and the natural children of the adopting parents (about 0.32) are low also argues for a high heritability of IQ. At least for the White population of the United States and Europe, heritability studies of various degrees of kinship consistently show that different genes are responsible for about 75 percent of the total differences in IQ. This is true even for brothers and sisters in the same home (remember, they share only about 50 percent of their genes—to be technically precise, 50 percent of their genetic variance— on average). (See Table 3.1 on page 94.)

Another result from these studies that is predicted by Jensen and those who attribute a major role to genes but that poses a problem to anti-Jensenists is that the heritability of IQ increases with age, while the correlation between adopted children and their adoptive parents and also the correlation between adopted children and the natural children of their adoptive parents both decrease with age. In this respect, IQ acts like height, obesity, tooth size, or any number of physical traits for which environment plays a major role early in development but for which genes—and usually several genes acting together—increasingly steer the course of development. Consider how the environmental factor of severe malnutrition or illness in infancy can permanently impair a person’s general health for the rest of his or her life, but may cause less devastating though still adverse effects if experienced later, when the body is more fully developed. And those of us who reach middle age become painfully aware of how much our family’s medical history becomes increasingly pertinent to our own probability of encountering such diseases and conditions as high blood pressure, cataracts, diabetes, stroke, cancer, or heart disease.

But the devil—and to many anti-Jensenists, a quite literal and evil one—is in the details. They argue that when identical twins are separated and placed in different homes, their environments are really not that different in terms of the critical factors. Rarely, they argue, is one identical twin placed with poverty-stricken parents on Skid Row while the other grows up in the lap of luxury on Park Avenue. They also question whether twins are even representative of the population as a whole. As an environmental factor tending to make twins more alike, anti-Jensenists point to the fact that twins share the same womb. In the case of adoption, they question whether adoptive parents really treat their adopted children exactly as they do their biological offspring. And they point out that in many cases the fact that these children are being placed for adoption may be evidence of early environmental problems, such as the use of drugs or alcohol by the mother (Jensen concedes that such biological problems are important).

The most powerful attempt to topple the second pillar of Jensenism was the notorious Burt Affair. The late Sir Cyril Burt, a founder of the hereditarian London School of psychology, had published a number of studies showing that the correlation in IQ for identical twins reared apart was 0.77. Jensen, in his 1969 Harvard Educational Review article, cited this figure and other similar findings by Burt on the inheritance of mental ability. After Burt’s death, a number of anti-Jensenists carefully scrutinized Burt’s published research. They noted that the correlations between twins hardly changed even after Burt claimed he had added new sets of twins to his database. Then similar discrepancies were uncovered in Burt’s other publications. Not only the anti-hereditarians but Burt’s biographer as well concluded that the aging scholar had begun to lose touch with reality and not only had cooked up the correlations but even invented nonexistent coauthors to support his claim of having conducted new research. Jensen counters that the work of two subsequent authors seems to have vindicated Burt, and more importantly, that even disregarding Burt’s results the preponderance of evidence supports the conclusion that about 75 percent of the variation in IQ is because of genes, not environment—a figure very close to Burt’s 0.77. Jensen then describes the state-of-the-art research that recently has identified some of the specific genes for IQ.

A Primer on Variance and Heritability

The methods of quantitative genetics allow us to determine the proportion of the variation in any measurable trait that is due to heredity and the proportion that is due to environment.

The easiest way to get some idea of the variation within any group of people and in any measurable trait—whether IQ , blood pressure, height, or weight—is to subtract the lowest figure from the highest. Statisticians refer to the difference between these two figures as the “range.” But even if there are many people in the group, as there are in most social science experiments, a single extreme case can distort this value. For example, if we were measuring variations in income, home runs hit in a season, or books sold, the inclusion of just one person at the top of the scale (e.g., Bill Gates, Barry Bonds, or Danielle Steele) would really inflate the range.

The next thing we might try would be to calculate an average (termed the mean) for the group and then to subtract the mean from each person’s score. The result would be a series of values that statisticians call “deviations from the mean.” For a score above the mean, the deviation would be a positive number; for a score below the mean, a negative number. To get some idea of the average deviation from the mean, we might just add all these deviations and then divide by the number of people we measured. But the sum of all the positive and negative deviations has to equal zero, and so the result would not tell us anything at all.

Since we’re interested in how much variation there is in the group, we’re really not concerned with whether the deviations from the group mean are positive numbers or negative numbers. Either way, they represent variation. The simplest and most direct approach in this case would be to ignore the signs (whether positive or negative), add up all the deviations from the mean, and then divide by the number of people in the group to get a value that represents the average deviation from the mean.

Statisticians have done essentially this, first squaring each deviation from the mean (that is, multiplying the number by itself), which makes all the values positive numbers. The squared deviations from the mean then are added together, and the sum is divided by the number of people in the group under study. The result is called the variance. (The widely used statistic known as the standard deviation is the square root of the variance.) Variance has a very important characteristic statisticians call “additivity,” which means that the total variance is always equal to the sum of its components.

There are complex mathematical reasons for using the squared deviations from the mean rather than simply ignoring the plus and minus signs. For the purposes of the present discussion, it’s enough to note that using the squared deviations allows us to compute the variance, which we can then break down into the percentage of the total variance due to genes and the percentage due to environment; and that these two percentages must add up to 100 percent (the total variance). As a very rough analogy, think of asking a financial advisor to go over your family budget. He breaks down your total monthly income into the percentage you must spend on necessities such as taxes, rent or mortgage, utilities, and car payments versus the percentage that you can either save or spend as you wish.

Analysis of variance is central to the way quantitative genetics estimates the relative roles of heredity and environment. The total variance in any trait is broken down into the proportion due to genes—called “heritability,” and represented by the symbol h2—and the proportion due to the environment, termed “environmentality,” and represented by the symbol e2. Both h2 and e2 can be further broken down into their components (just as the percentage of spending on necessities and on niceties could be broken down further in the family budget analogy). The sum of these components must always equal the total variance.

An Example

Suppose we were testing a group with only four subjects. (Real studies use many more.) Let’s call them A, B, C, and D.

Their systolic blood pressure readings (or their tested IQs) are:

A = 100; B = 120; C = 90; and D = 90.

The mean is:

(100 + 120 + 90 + 90 = 400)/4 = 100

The deviations from the mean are:

A = 100 – 100 = 0
B = 120 – 100 = 20
C = 90 – 100 = –10
D = 90 – 100 = –10

Note that the sum of these deviations equals zero:

0 + 20 + (–10) + (–10) = 0

The squared deviations from the mean are:

A = 0² = 0
B = 20² = 400
C = –10² = 100
D = –10² = 100

The variance in our group, then, is:

(0 + 400 + 100 + 100)/4 = 600/4 = 150

So the standard deviation in our example is equal to the square root of 150, which is approximately 12.25.

The Important Things to Remember
About Variance and Heritability

The proportion of the total variance in any trait that is due to genes is termed the heritability of the trait and is represent by the symbol h².
For example, if we find that differences in genes explain 80 percent of the variation in blood pressure in a group of people, the heritability of blood pressure in that group is 0.80 (h² = 0.80).
The heritability of 0.80 refers to the variation in blood pressure in that group—not the percentage of the blood pressure reading for any individual in the group—that is due to genes rather than environment.
Further, h2 = 0.80 is the heritability in that group. Blood pressure (or IQ or any trait) could have a different value if we tested a different group.
However, heritability studies of IQ have been largely consistent in reporting values of h2 from 0.50 to 0.80, even for different countries or different races or ethnic groups.
Whatever proportion of the variance is not due to genes (1.00 – h²) is due to the environment.
The proportion of the total variance in any trait that is not due to genes is termed the environmentality of the trait and is represented by the symbol e². In our example, 20 percent (that is, 100 percent – 80 percent) of the variation in blood pressure would be due to the environment. (To be technically precise, 1.00 - h²= e²+ measurement error. For IQ and other psychological tests, the error is usually between 5 and 10 percent. Medical measures such as cholesterol level, blood pressure, and X-ray interpretation often have higher measurement errors. Even reading length from a ruler involves some measurement error.)
In human research, the environment includes not only socioeconomic factors such as income, quality of schools, and years of education, but also biological factors such as exposure to toxic chemicals, and injuries during pregnancy.
Both heritability and environmentality can be broken down further into components. But no matter how detailed the breakdown, the components must add up to the total variance (that is, the total variance must equal the sum of its parts).

Miele: Well, if the first tenet of Jensenism—the g factor, which we talked about in Chapter 1—isn’t controversial, I hope you’re not going to tell me that the second tenet—that the differences in g are more the result of heredity rather than environment—isn’t controversial either.

Jensen: The fact that g is more strongly genetic than most other psychological variables is not really controversial among empirical researchers in this field. It is highly controversial only in the popular media. Just try to find any real controversy among the experts who know the research on this issue. There’s always a handful of dissenters regarding any body of empirical knowledge, of course, even in the scientific community. Unfortunately, the mass media have presented the views of this small number of highly vocal dissenters as the prevailing position.

Miele: No matter which side I talk to on issues like this I find there’s only one thing the two sides agree on—blaming the media that their side isn’t accepted and the other side is given any voice at all. Can you provide any solid evidence to support your claim of media bias?

Jensen: Anyone who wants a thorough presentation of expert opinion among behavior geneticists and psychometricians on the subject and a scholarly analysis of the popular media’s distortion of it should read The IQ Controversy: The Media and Public Policy by Mark Snyderman and Stanley Rothman.

Miele: Again, I’ve found that both sides in any controversy point to books that they claim set the record straight. What makes Snyderman and Rothman’s book the definitive statement? It wasn’t published by the American Psychological Association (APA) or the Behavior Genetics Association (BGA), was it?

Jensen: No, but they came to their conclusions after surveying those best qualified to judge, the members of the Behavior Genetics Association and the Tests and Measurements Division of the American Psychological Association. And an article summarizing their findings and conclusions was published in American Psychologist, the APA’s house journal.

Miele: Are you telling me that if I did a content analysis on the most popularly used Psych 101 textbooks or polled the members of the APA, I’d get a paraphrase of what you just told me?

Jensen: I’m not sure what you’d get from a random poll of the APA membership. But if you polled experts in biological psychology, comparative psychology, behavioral genetics, and psychometrics, you would find a solid consensus that individual differences in IQ and the g factor have a large genetic component. The APA itself has published an introduction to the genetics of individual differences, Nature, Nurture, and Psychology, edited by Robert Plomin and Gerald McClearn, which also agrees with that consensus.

Miele: And is that consensus reflected in psychology textbooks?

Jensen: I’m afraid it is not. I recently examined the chapters on intelligence and individual differences in a sample of introductory psychology textbooks. The conceptual errors and misinformation in their discussions of the heritability of IQ are appalling, even in some of the most widely used textbooks. There are a few exceptions, but on the whole, undergraduate psychology textbooks are misinforming hundreds of thousands of college students on this subject every year. This has gone on for at least 30 years. The disparity between specialist books in this field and the treatment of the subject in most undergraduate texts is scandalous. Students might as well read pop psychology articles in the Sunday newspaper supplements.

Miele: You seem to have little but contempt for introductory psychology texts and to get awfully worked up about them. Why?

Jensen: I’d rather have students read William James’s Principles of Psychology, originally published in 1890, than to read the pabulum now passed off on undergraduates as “Introductory Psychology.” And the introductory course has a considerable influence on who will and who won’t major in psychology. I still read James for pleasure now and then, but it almost sickens me even to thumb through most of the introductory psychology books published in recent years. They represent a dumbing-down of the whole field! I doubt that textbooks of this ilk exist in the biological or physical sciences, because they wouldn’t be tolerated by either the students or the faculty. Of course there are a few perfectly respectable introductory texts in psychology. It is up to instructors to be discriminating and search for them.

Miele: Perhaps part of the problem comes from the origins and associations of the words. Before the scientific term “heredity,” we had the word “hereditary.” “Hereditary” can mean “genetic, not environmental”; but it can also mean “by right of birth,” as in “the hereditary Duke of Northumberland.” The term “genetic” is easily confused with “eugenics.” Do you think the origins and associations of the words “heredity” and “hereditary” with aristocracy, and later, of “eugenics” with Nazism, have cast a dark cloud over the scientific study of mental ability?

Jensen: They shouldn’t, but I’m sure they have cast a shadow, if not your dark cloud. And hopefully our increase in scientific knowledge is clearing the skies. “Heredity” simply refers to the transmission of genes from parents to their offspring; genes are the physical units of heredity. “Hereditary” means about the same thing, but often implies the passing on of parental genes that affect some observable characteristic of one or both parents to one or more of their offspring. A “hereditarian” is someone who holds that some part of the variation in mental and behavioral as well as physical traits is attributable to genetic variation within the species. The word “genetic” pertains to genes, or to characteristics known to be influenced by genes.

Miele: And “eugenics”?

Jensen: When Sir Francis Galton coined the word “eugenic,” which literally means “good beginning” or “good genes,” he meant the hereditary basis of characteristics such as good health, longevity, the absence of birth defects or physical or mental handicaps, personally and socially advantageous mental abilities, and favorable personality traits.

To dispel any Third Reich or Holocaust guilt by association implied in your question, let me quote exactly what Galton said about eugenics in his autobiography, Memories of My Life:

Man is gifted with pity and other kindly feelings; he has also the power of preventing many kinds of suffering. I conceive it to fall within his province to replace Natural Selection by other processes that are more merciful and not less effective. This is precisely the aim of Eugenics.

Even if we don’t use the term, eugenics is practiced throughout the civilized world today through genetic counseling, amniocentesis, and DNA testing for various genetic diseases such as Tay-Sachs, Huntington’s chorea, and many other genetic anomalies. And it is the prospective parents who are requesting these family planning procedures. Government is not ordering them. What opposition there is these days comes from a few on the political left and many more on the religious right.

Miele: You still haven’t answered the second part of my question— Do you think all this talk of genes and heredity, and its association with aristocracy, eugenics, and even Nazism, have forever bedeviled the scientific study of the nature of mental ability?

Jensen: No, I don’t believe that the scientific study of the inheritance of mental ability is really bedeviled by these wrong or evil things from past history. I don’t put the Galtonian conception of eugenics, as stated in the quote I gave you, in that category. Nor do I see any intrinsic relationship between aristocracy or Nazism and the scientific study of the g factor, behavior genetics, and individual or group differences.

There are those, however, who for whatever reason deny the reality of individual differences or the evidence that individual differences have genetic as well as environmental causes. Some have tried to link psychometrics and behavioral genetics with Fascism, Nazism, Hitler, or whatever and hereditarian psychologists have been subjected to such defamatory propaganda. The New York Review of Books review of my 1980 book Bias in Mental Testing (whose findings were subsequently confirmed by a special committee of the National Academy of Sciences) ran with a cartoon of me in what looks like a Nazi storm trooper uniform! And a Canadian psychologist who studies the evolutionary basis of racial differences in mental ability was caricatured in a newspaper cartoon as shaking hands with Hitler. That abysmally low level of criticism merely shows their desperation. They aren’t worth recognizing.

Miele: Okay. Then let’s get back to the technical term used in behavior genetics, “heritability.”

Jensen: Here we have to shift gears drastically, because “heritability” means something very different from the terms “heredity,” “hereditary,” and “inherited.” I’m willing to bet that only a minority of Ph.D.’s in psychology know the definition of “heritability.” So let’s get its meaning straight right now.

Technically, “heritability” is defined as the statistically estimated proportion of the population variance in a given trait that is attributable to genetic factors. Variance (Var.) is calculated as the arithmetic average (or mean) of all the squared deviations of each individual measurement from the overall mean of all the measurements. [See the Primer on Variance and Heritability that begins on page 74, after the introduction to this chapter.]

Here’s the key point: The heritability of any trait is the proportion of the total trait variance due to genetic variance. As a very rough analogy, think of the pie charts showing federal revenue you see in the newspaper that show, say, 25 percent comes from corporate income tax, 70 percent from individual income tax, and the remaining 5 percent from excise taxes, tariffs, and inheritance tax.

Geneticists make a further distinction between narrow heritability and broad heritability. Technically, narrow heritability is the proportion of total variance due to the additive effects of genes only. Broad heritability consists of the narrow heritability plus the variance resulting from genetic interactions whose effects are not simply additive (that is, not 2 + 3 = 5, but 2 × 3 = 6); from assortative mating (the tendency of like to marry like, which increases total variation); and from a very special component called genotype-by-environment (G × E) covariation. G × E covariation refers to cases in which genes and the environment are both favorable (or unfavorable) for the development of a particular trait, as in the case of a child who is genetically gifted musically and also grows up in a highly musical environment, like Mozart.

Miele: So are you saying that heritability can cut the nature-nurture Gordian knot? What about the classic example of the same seeds sown in different soils that goes back to Charles Cooley, the founder of the American Sociological Association? Or maybe back even further, to Jesus in the Parable of the Sower and the Seeds:

Behold the sower went out to sow. And as he sowed, it happened one indeed fell by the roadside; and the birds of heaven ate it. And another fell on the rocky place where it did not have much earth. And it sprang up at once, due to not having deepness of earth. And the sun rising it was scorched. And through not having root, it was dried out.

And another fell among the thorns, and the thorns grew up and choked it, and it did not yield fruit. And another fell into the good ground and yielded fruit, going-up and increasing; and one bore thirty, and one sixty, and one a hundred-fold. (Mark 4:3–8)

Jensen: I love your apt quotation from the New Testament. Its poetic language offers a welcome relief from all my technical terminology. And today’s behavior genetic research pretty much tells us the same thing.

Essentially, heritability estimates do cut the nature-nurture Gordian knot for any measurable traits by separating the total variation into the part due to variation in genes and the part due to variation in environment. I prefer the terms “genetic influences” and “nongenetic influences” because so many people think environment means just the psychological, social, and cultural milieu in which a person grows up. These nongenetic influences begin virtually at the moment of conception. They have direct effects on the brain’s development and are probably the most important of all environmental effects on g. They include intrauterine conditions related to the mother’s age, health, and blood type; incompatibility between mother and fetus; nutrition; certain medications; and substance abuse. Then there are perinatal conditions such as anoxia, birth trauma, and extreme prematurity. And also postnatal conditions—mainly early nutrition and the various childhood diseases. My analysis of IQ differences in MZ (monozygotic, or identical) twins, who have the same genes, suggests that nearly all these effects are disadvantageous.

Miele: But does that mean that factors like home environment, parent-child interaction, schooling, and family income have no effect on a person’s g?

Jensen: No, later environmental influences have their effects largely on what a person does with his or her level of g rather than on the level of g itself. These effects are fully recognized by geneticists—the sources of environmental variance are every bit as interesting to them as the genetic variance. The important point is that by means of quantitative genetic analysis, such as the calculation of heritability, we are able to get good estimates of the relative strengths of the environmental and the genetic influences on a given characteristic in a given population at a given time. And by the same means we can look at the relative effects of genes and environment on a particular trait over the course of development, from infancy to later maturity.

Miele:That all seems so contrary to everything we’ve come to believe about the importance of education. Do you have any evidence to support those statements?

Jensen: Consider the heritability of height. In our population, height has a heritability of about 0.30 in infancy, which gradually increases, up to about 0.95 in early adulthood. IQ shows a similar developmental increase in heritability, going from about 0.40 in early childhood to about 0.70 in adulthood, then up to about 0.80 in older adults. If environment and experience were the chief determinants of mental growth throughout our life span, you would predict that the longer we have lived, the lower the heritability of IQ, because the difference between our life experience and those of our kin should accumulate. But just the opposite is found to be true. IQ behaves like height and other physical traits in that the resemblance between genetic relatives increases with age, despite their differences in cumulative life experience.

Miele: But critics point out that heritability estimates are dependent on the population studied and the conditions under which that population developed. Don’t those qualifications dull the edge of the behavior genetic knife? Rather than cleanly cutting the nature-nurture Gordian knot, what we see is a fuzzy and frayed tangle.

Jensen: Those critics write as if behavioral geneticists weren’t aware of these points. The basic genetic model is that the total variance we see in any trait, termed the phenotypic variance (var.P), is composed of the genetic variance (var.G) plus the nongenetic variance (var.E), also called the environmental variance, or

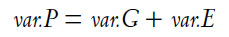
Heritability (h²) is simply the ratio of the genetic variance to the total variance:

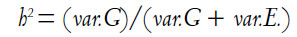
So by definition, heritability can vary over some range of values depending on the degree of genetic variation in the population (var.G) and the amount of environmental variation (var.E). If you look at the second equation, you can see that the smaller var.E becomes, the higher h2, until you reach the point at which there is no environmental variation at all (that is, var.E. = 0.00), at which point h2 = 1.00. As var.G gets smaller, h2 also decreases, until h2 = 0.00 and e2 = 1.00 – h2 = 1.00 – 0.00 = 1.00. If everyone’s environment is pretty much the same, heritability will be very high because the only thing that really varies is the genes. Likewise, if there is very little genetic variation, as for example in highly inbred strains of corn or laboratory mice, heritability will be very low. In a country where part of the population suffers from malnutrition while others are well fed, the heritability of height is lower (because of greater environmental variation) than in a country where everyone is reasonably well nourished.

The other point about heritability follows as a corollary—a heritability estimate is not a constant like the speed of light, nor is it meant to yield some single, constant value. Rather, heritability is an inherently inconstant population statistic, like the average birthrate, the average mortality, or the average height of adult men or women. The heritability of IQ estimated in different studies varies as a function of the test used, the age of the subjects, and the degree to which the subjects vary in socioeconomic status and educational level. The heritability of IQ fluctuates somewhat from sample to sample and study to study from about 0.40 to 0.80, with the average for all studies falling somewhere between 0.60 and 0.70. But such an overall average isn’t really as informative as knowing the heritability in a particular population under specified conditions.

Miele: But I’ve heard Jerry Hirsch, a distinguished psychologist who’s done some pioneering work in behavior genetics, say that heredity is a fact but heritability estimates are just hand waving that implies greater certainty than really exists. And he quotes no less an authority than Sir Ronald A. Fisher, who developed many of the methods of quantitative genetics, to support his criticism.

Jensen: I just explained why uncertainty is inherent in any heritabil-ity estimate. No one who knows anything about Fisher’s views could imagine that he would disagree with anything I’ve said on this subject. Fisher merely pointed out that a properly estimated heritability coefficient is a population statistic, and, like any population statistic, it has a clearly definable probable error—that is, its likelihood of being off the mark by a given amount. The same thing is true for just about every scientific measurement, say a statistical determination of the birthrate in the U.S. population in the year 2002. Would you then echo Jerry Hirsch and say that a newborn child really exists, but the birthrate is just hand-waving?

Miel: Since we can’t and wouldn’t want to perform controlled breeding experiments with humans, our knowledge about the roles of Miele: heredity and environment and the heritability of mental ability comes from comparing identical twins, nonidentical twins, other relatives, and adopted children.

Before summarizing the results of those studies, could you sketch the logic behind those studies?

Jensen: I covered this material in depth in the courses on behavior genetics and on theories of intelligence that I taught at the University of California at Berkeley. It says something about the social sciences in contemporary America that after my retirement no one was hired to teach these courses in either the psychology or the education departments.

Most of the statistical methodology was originally developed to solve problems in genetics, especially as applied to agriculture. But it’s just as applicable to the field of behavior genetics, which came into its own in the 1970s with the formation of the Behavior Genetics Association (of which I was a charter member) and their journal Behavior Genetics, in which I have published a number of articles.

Miele: Okay. Let’s try a really short course, for now.

Jensen: Well, the essential ideas did indeed come from Sir Ronald A. Fisher’s elaboration of the basic principles of heredity discovered by Gregor Mendel, which we call Mendelian genetics. Mendel dealt entirely with traits in which variation is due to a single gene locus that can take two distinct forms—like his wrinkled peas or smooth peas, or red flowers or white flowers. If you grow these flowers in a uniform environment (which Mendel did) you get either two or three distinct variants, depending on whether the trait manifests either genetic dominance (where the offspring appear just like the dominant parent but show no trace of the recessive parent) or genetic additivity (where the offspring display a blending of the two parental forms).

Jensen’s favorite photo of himself because "it shows me in my most typical setting and activity" — in his study at home, working on another article or book. (Taken but never used by Life magazine)

Let’s say we have a gene with two possible forms (termed “al-leles”)— and let’s call one R (for Red) and the other w (for White)— that determine the color of the flowers. Each flower has two alleles for color (R and w), with one allele coming from each of its two parents. Then each flower must have one of the following four possible allele combinations (technically termed “genotypes”): RR (Red-Red), ww (White-White), Rw (Red-White), or wR (White-Red). The RR genotype is pure red (technically termed “homozygous”), and its phenotype (that is, what we observe) is a red flower. The ww genotype is pure white (again homozygous), and its phenotype is a white flower. The wR and Rw genotypes (technically termed “heterozygous”) are the same; their different designations simply indicate that a different parent provided the allele to the offspring (which for our present purposes doesn’t matter).

Now, the genotypes of the offspring of one of our pure red RR flowers and a pure white ww flower can be either RR, Rw, wR, or ww. Let’s suppose flower color has genetic dominance and red is dominant over white. Then the RR, Rw, and wR genotypes all result in the Red phenotype (that is, a red flower). Only the pure white ww genotype produces the phenotype for a white flower. Given sufficient numbers, about three fourths of the offspring of pure red flowers and pure white flowers will be red flowers and the remaining one fourth or so will be white flowers—the 3:1 ratio Mendel described. Many blood types in humans also show genetic dominance.

But now suppose we’re dealing with a different trait, say, stem height at maturity. We again have two homozygous, or pure, strains. Let’s call them TT (homozygous tall) and tt (homozygous short). Now, the genotypes of the offspring of one of our homozygous tall TT flowers and a homozygous short tt flower can be either: TT, Tt, tT, or tt. Unlike color, stem height has additive inheritance—that is, neither T nor t is dominant or recessive, but instead they blend. The homozygous tall TT genotype produces the tall phenotype. The homozygous short tt genotype produces the short phenotype. The heterozygous Tt and tT genotypes, however, produce plants that are intermediate in height between the two parental strains. So for stem height, the offspring would display three phenotypes, not two as was the case for color. About one fourth would be tall, one-half would be intermediate, and one fourth would be short. Important human traits such as height and IQ show polygenic, rather than simple Mendelian, inheritance.

Miele: The ratios you’ve given are statistical. They’re what you see with sufficiently large numbers. If I start breeding a couple of pea plants out on my balcony I’m not going to see these exact ratios in each and every generation. Right?

Jensen: Of course. That’s one of the defining properties of quantitative genetics—its predictions are probabilistic. That means that our experiments in human behavior genetics require statistical inference. And this often makes the results harder to explain and harder for nonspecialists to understand. But it also means—and this is important in relation to a lot of your earlier questions about the historical and political associations of the nature-nurture problem—that the antiquated ideas about trying to breed a master race and so on just don’t make any scientific sense in terms of modern genetics. What we can do genetically, even when and if we would want to, is really rather modest.

And there are always trade-offs, even when we do apply selective breeding. Consider the “green revolution” that developed grains with higher yields. They’ve been achieved by selecting for only one or two genetic characteristics, such as kernel size or oil content, in very standardized environments. But human behavior is the result of thousands of genes and develops in all sorts of environments, including environments our individual genetic tendencies lead us to select or create for ourselves. The human genome has about at least 30,000 and perhaps twice that many genes. The central mechanism of behavior is the brain, and at least half of all the genes in the human genome are involved with the brain, and the effects of about one third of all the genes are entirely unique to the brain.

Miele: Anything more in your short course in genetics?

Jensen: Yes, one more thing, about genetic dominance. The genes for the characteristics that prove to be advantageous to survival over the course of natural selection are usually dominant genes, while the characteristics that prove disadvantageous are usually recessive. The two mechanisms that cause this are spontaneous mutation and natural selection. Most mutated genes confer undesirable characteristics (that is, phenotypes) in their homozygous (that is, “pure”) combination. They remain recessive, and selection very gradually reduces their frequency until it is nearly at the rate of spontaneous mutations for that gene. Mutations that confer some selective advantage, or Darwinian fitness, increase in frequency over successive generations and are dominant over the less advantageous alleles at the same locus, which are therefore said to be recessive.

For some traits, however, it is most advantageous to maintain intermediate values. So selection favors the preservation of alleles with additive effects, producing more intermediate phenotypes (like the peas of intermediate height in the previous example). Physical size, or stature, is an example of this; the average for a given species generally has a biological advantage over either extreme. Another example is the heterozygous condition for sickle-cell anemia. The homozygous condition produces a genetic disease, but the heterozygous condition confers a relative immunity to malaria. That isn’t important in modern technological society, but when slash-and-burn agriculture was spreading through Africa there was probably selection favoring the heterozygous condition. This example also points out how complex the interplay between heredity and environment can be.

Miele: Let’s get back to intelligence and mental ability. As you said, it’s obvious that a simple inheritance model based upon two alleles— smart and dull—just doesn’t fit.

Jensen: Right. Most of the human traits of greatest interest to psychologists are not Mendelian. Individual differences and group differences in these traits are not attributable to a single gene with two alleles. The variation in these traits does not consist of only two or three discrete types, as in Mendelian characters (like blood type), but of continuous, quantitative gradation throughout the whole range of variation, from the lowest to the highest. The genetic underpinning of continuous or quantitative traits is polygenic, which only means that more than one gene is involved in the trait variation. The number of genes for a polygenic trait may range anywhere from two genes on up into the hundreds. For most polygenic traits, the number of genes is not known, but there are ways theoretically to make a rough estimate of this number for a given trait.

Miele: So how can genetic models deal with the human behavioral traits you’ve just said were so complex?

Jensen: This problem was also solved by the British geneticist and statistician Sir Ronald Fisher in one of the landmark papers in the history of genetics. “The Correlation Between Relatives on the Supposition of Mendelian Inheritance,” published in 1918, laid the foundation for quantitative genetics (the genetics of continuous, polygenic traits as contrasted with single-gene or Mendelian traits).

Fisher proposed that quantitative traits are determined by a whole set of genes (that is, they exhibit polygenic variation) and that the alternate alleles for each gene in the set slightly increase or slightly decrease the observed phenotype from the population mean of that trait, but the simple Mendelian laws hold for each of these genes. For example, suppose that stem height was not the result of just the two alleles for one gene (T and t, as in the model above), but three genes with two alleles each: (S and s), (T and t), and (U and u). The alleles S, T, and U each slightly increase stem height from the population mean, while the alleles s, t, and u each slightly decrease it.

Given these explicit conditions and a set of mathematical formulas (known as “Mendelian algebra”), Fisher calculated the theoretical genetic correlation between any degree of kinship (for example, parent-child, identical twins, fraternal twins, siblings, first cousins, and so on) for any polygenic trait in any species of humans, or any sexually reproducing plants or animals. To take the simplest case, MZ (that is, monozygotic or identical) twins share the exact same set of genes because they both develop from the division of a single fertilized egg. So according to Fisher’s formulas, their theoretical correlation on any heritable, quantitative trait (such as height or IQ) is +1.00, as it would be for any individual with themselves or with their clone. The theoretical correlations for DZ (that is, dizygotic or fraternal twins, whether of the same sex or opposite sexes), parent-child, and full siblings are all +0.50 because these kinships all share, on average, half of their genes. The correlations predicted by Fisher’s formulas continue to decrease as the degree of kinship decreases. For unrelated individuals, the predicted correlation is 0.00, though this would not hold for remote, small villages whose members are all related or in pure breeds of dogs, thoroughbred horses (who all derived from a handful of ancestors), laboratory mice, or inbred strains of corn, rice, or other plants.

Those are the theoretically predicted correlations based on genetic similarity. The actual correlations we find when we test pairs of MZ twins or DZ twins, or groups of siblings, cousins, or unrelated individuals, can vary continuously from –1.00 (that is, exact opposites— the higher one member of the pair scores or measures, the lower the other does) to 0.00 (no greater resemblance in their scores than between pairs of random numbers) to +1.00 (perfect parallel— the higher one member of the pair scores or measures, the higher the other does, as well).

Table 3.1 compares the predicted correlations for the various degrees of genetic similarity against the actual correlations found by behavioral genetic research.

Male: And how do these figures help us to resolve the nature-nurture uncertainty?

Jensen: By comparing them against the correlations we actually find in behavior genetic studies of mental ability and other psychological traits to see how well they fit. It turns out that they closely fit the genetic predictions and do not fit predictions we would make from a purely environmental theory. There is no valid environmental explanation, for example, for why identical twins reared apart should be almost as alike as identical twins reared together and much more alike than fraternal twins or ordinary siblings reared together; or, on the other hand, why unrelated adopted children reared together should be so unlike. There are all sorts of statistical tests you can use to validate the genetic model, but I’ve given you the big picture. The genetic model, which also takes account of environmental factors, fits the observed facts, while a purely environmental model fails.

TABLE 3.1 Predicted and Actual Correlations in IQ for Various Degrees of Kinship

Degree of Kinship	Predicted:	Actual:
Identical (MZ) twins reared together (Same genes in same home environment)	1.00	0.86*
Identical (MZ) twins reared apart (Same genes in different home environments)	1.00	0.78*
Fraternal (DZ) twins reared together (50% same genes in same home environment)	0.50	0.60*
Full siblings reared together (50% same genes in same home environment)	0.50	0.47*
Full siblings reared apart (50% same genes in different home environments)	0.50	0.24*
Natural parent-child in same home (50% same genes in same home environment)	0.50	0.42*
Natural parent-child adopted by other home (50% same genes in different home environments)	0.50	0.24*
Adopted siblings reared together (Different genes in same home environment)	0.00	0.32†
Parent-adopted child (Different genes in same home environment)	0.00	0.19†

* These correlations, which contain a genetic factor, increase with age.

These correlations, which contain only an environmental factor, decrease with age. †

SOURCES: The predicted correlations are those derived from the simplest genetic model and taken from: "How Much Can We Boost IQ and Scholastic Achievement?" Harvard educational review 39, Winter 1969, p. 49. The actual correlations are those summarized from various sources and reported in Robert Plomin, et al., Behavioral genetics (4th edition), (New York: Worth Publishers, 2000).

Miele: So then is the best estimate of the heritability of intelligence the average of all these studies, about 0.60?

Jensen: No, not really, because the average estimate of heritability is based on the combined heritability estimates of IQ for every age group, and it is now known that the heritability of IQ increases with age, going from about 0.30 in very early childhood to about 0.70 in early maturity and up to about 0.80 in later maturity. The older we become, the more the phenotype reflects the genotype. A strictly environmental theory would predict just the opposite, so the increase in the heritability of IQ with age is another case where the genetic model fits the facts and the purely environmental model fails.

When we talk about a best estimate of heritability, we have to specify an age group. Various mental tests do not yield equivalent heritability estimates, either. Virtually all IQ tests are highly g loaded, but some are purer measures of g than others. Generally, the more a mental test measures the g factor, the higher is its heritability. This fact also provides evidence for the biological, rather than merely statistical, reality of g.

Miele: So how do we best estimate the heritability of IQ, and what is its value?

From studies of identical twins reared apart. In all the published studies of pairs of MZ twins separated in infancy, put out for Jensen: adoption, and reared entirely apart, the average correlation between the IQs of the twins in adulthood is 0.75. Since the twins did not share a common environment but do have identical genes, this correlation provides a fair estimate of the heritability of IQ for people in the normal range of environments for our population. At the other extreme from MZ twins reared apart are unrelated adopted children who are reared together like full siblings. In early childhood their IQs correlate about 0.25, but by late adolescence the correlation drops to nearly zero. This shows that the shared environment in which they both were reared has virtually no lasting effect on their IQs. The IQs of full siblings reared together, however, correlate about 0.47, which is close to their theoretically expected genetic correlation of +0.50.

Miele: Don’t these figures show that environmental factors are also important?

Jensen: Yes, but the most powerful environmental effects are not part of the shared family environment. These effects occur within families, not between families, and make up what is often referred to as the “nonshared environment.” I prefer to call it “nongenetic,” because I believe it has much less to do with the psychological or social environment than with what I call the “biological microenvironment.” It consists of all environmental effects that have biological consequences, particularly on the neural basis of mental development, beginning at conception. They are largely accidental or random. Each single effect is usually too small to be detected, but if they accumulate over the course of development from conception to maturity they can become evident.

These microenvironmental effects may contribute as much as 20 or 25 percent of the total variance in IQ in the population. Because they are more or less random, they are difficult to remedy or control. Their occurrence has probably been reduced in recent decades by improved nutrition of mothers and children, advances in obstetrical techniques, inoculation against the common childhood diseases, and improved health care in general. Most of the population in Third-World countries and in some small subpopulations in the United States and other industrialized countries have not had the benefits of these nutritional and health-care measures, and this probably affects their mean IQ. The reduced occurrence of these unfavorable microenvironmental elements in the industrialized countries is probably one of the causes of the gradual rise in mental test scores in these countries during the last 60 or 70 years.

Miele: In theory, identical twins share 100 percent of their genes. We can usually tell they’re identical just by looking at them. So the physical traits are largely genetic. But doesn’t the fact that they look so much alike also mean that they’re treated more alike by their parents, by schoolteachers, by society at large? Doesn’t the self-fulfilling prophecy factor confuse the effects of heredity with those of environment?

Jensen: There is no evidence at all that people looking alike makes their IQs more alike. Dizygotic (DZ) or fraternal twins are genetically no more alike than ordinary siblings; their genetic correlation is 0.50. However, like other siblings, some same-sex DZ twins look much more alike than others. In some cases their parents even wrongly believe that their DZ twins are identical twins, and they treat them as such by dressing them alike and giving them the same hairstyles, and so on. But DZ twins whose parents and others had mistaken them for MZ twins are no more alike in IQ than other DZ twins or ordinary siblings who don’t look much alike.

If those who really believe that the IQ correlation between MZ twins is better explained in terms of their physical similarity than in terms of their genetic correlation, they should go out and find unrelated people who look alike, such as movie stars and their doubles, and determine the correlation between their IQs. That would put this theory to the acid test. The safest bet imaginable would be that the correlation comes much closer to the correlation between pairs of people picked at random (that is, about 0) from the general population than the correlation between MZ twins reared apart (that is, about 0.75). Of all the failed attempts I’ve ever heard to explain away the importance of genetics in individual differences in intelligence, the look-alike theory is the most absurd.

Miele: Some of the studies of identical twins reared apart that you and other hereditarians use to estimate the heritability of IQ were conducted by the famous British psychologist Sir Cyril Burt. A number of scholars carefully scrutinized Burt’s published research. They questioned how the correlations between twins changed so little even though Burt claimed that he had added new sets of twins to his database and concluded that Burt just “made up” the correlations. Did you ever question Burt’s twin studies? Do you think he “faked” his twin data? Hasn’t the Burt Affair cast a shadow over twin studies?

Jensen: Because of these suspicions, Burt’s twin correlations are no longer cited in any summaries or discussions of the heritability of IQ. Two extremely thorough independent investigations of the accusations against Burt, however, have found these claims of faked or fraudulent data to be wholly unsubstantiated. To the best of our knowledge, the charges against Burt are false. For a time they seemed plausible because there are a considerable number of numerical errors in Burt’s later published reports. Virtually all of Burt’s errors are in articles he published when he was in his late 70s and 80s (he died at age 88) and are probably inadvertent, careless errors because about the same rate of numerical errors, things like transposed page numbers and the like, occur in the reference citations in his articles.

Miele: So that lets Burt off the hook? How about the way the correlations remain so constant, even though the articles show different numbers of twins were examined?

Jensen: The fact that the MZ twin correlation was 0.77 in three different reports is not too surprising for cumulated, overlapping data Jensen: sets. Burt’s value of 0.77 is very close to our best estimate for this correlation. A number of other studies of MZ twins reared apart have reported correlations of 0.76 and 0.78, and no one claims those studies were “faked” or the numbers were “cooked.”

No one with any statistical sophistication, and Burt had plenty, would report exactly the same correlation, 0.77, three times in succession if he were trying to fake the data. One noted scientist laughingly told me that when he and his colleagues found a correlation of 0.78 for the IQs of MZ twins reared apart, they were grateful as hell that the correlation didn’t turn out to be 0.77! In view of these recent findings, if Burt did fake his data, we’d have to credit him with clairvoyance.

During Burt’s long and influential but controversial career, he seemed to have made more enemies than friends, and I believe that was probably part of his problem. His autocratic and egocentric personality hardly endeared him to people. His most vociferous detractors included both those who disliked him personally and those who disliked the idea that human mental ability is so highly heritable as Burt had claimed. However comforting it seemed for Burt’s opponents to suggest, and perhaps even believe, that Burt “cooked” his data, more recent research has proved Burt to be correct and his detractors flatly wrong. One commentator likened the latest phase of the nature-nurture IQ debate to “a stomping match between Godzilla [that is, genes] and Bambi [that is, environment].” Much has been written about the Burt scandal for those who may be interested in the details.

Miele: Leon Kamin, one of the principal critics of Burt’s work, yours, and hereditarian research in general, once claimed that you only admitted that Burt’s twin correlations were faked—an admission you’ve now told us you’ve taken back—and took credit for finding the fraud, after he [Kamin] called you on it in a debate. That’s a pretty serious challenge to your scientific integrity and competence! Any comment?

Jensen: Here are the details. You decide.

After Burt died, I went to London and obtained from Burt’s secretary reprints of all of the papers Burt ever wrote on twins and other kinships in his studies of the heritability of IQ. As these were scattered in many different journals, I thought it would be of value to behavioral geneticists to have all of Burt’s data summarized in a single article. In preparing this article, which consisted of listing Burt’s correlation data for each type of kinship in separate tables, the numerical errors in his reports became clearly apparent; I found some 20 such errors, including the three correlations of 0.77 or 0.771 that Kamin suspected were fraudulent because they all had the same value. I wrote a detailed article on Burt’s errors and submitted it to the British Journal of Psychology. After a long delay, they rejected it and I submitted it to Behavior Genetics, which published it the same year that Kamin’s book came out. When I learned that Kamin, in an address given I believe at a meeting of the Eastern Psychological Association, had mentioned three of Burt’s errors as the basis of his claim of fraud, I credited Kamin for this observation in a footnote in my paper in Behavior Genetics.

If I have behaved in any way dishonorably with respect to the Burt affair, I’d like to know just how. If anything, I was too quick to come to accept that Burt’s data were “cooked” based on the information given in Hearnshaw’s biography. When further, more careful investigations revealed the lack of any solid evidence of fraud, I, of course, reversed my opinion.

Miele: Returning to the science involved, why doesn’t your estimate of the heritability of intelligence of about 0.76 agree with the estimate of about 0.50 that appeared in the prestigious British journal Nature? Surely that isn’t a case of media bias. It still indicates a significant genetic factor, but it’s substantially lower than the figure of 0.75 to 0.76 that you and other hereditarians keep repeating. And there are also arguments that the only really conclusive estimate of the heritability of intelligence comes not from Thomas Bouchard’s Minnesota Twin Project or the other similar studies but from the work of geneticists C. R. Rao and Newton Morton. It used a method known as path analysis, which the authors say is the only way to take cultural factors properly into account. So who’s right?

Jensen: Setting up a genetic model that encompasses all of the various degrees of kinships on which there exists suitable IQ data always involves certain assumptions. Different models that use different assumptions result in somewhat different estimates. The more detailed and fine grained the model, the more equations and assumptions it requires. The technical disagreements largely concern these assumptions, rather than the actual data per se.

The analysis in Nature that you mentioned hypothesizes a maternal effect that would make MZ twins more alike because they share the mother’s womb during the nine months of pregnancy. Since it is an environmental, not genetic, effect, it reduces the estimate of heritability. But other behavior geneticists argue that most of what happens during pregnancy makes twins more different, rather than more alike, and thus causes us to underestimate the true heritability.

But even if the heritability of IQ is 0.50 rather than 0.78 (or 0.70, 0.75, or 0.77), it still shows that there is a significant genetic component to individual differences in mental ability. That is a far cry from saying that IQ differences are largely the result of social, economic, and cultural factors.

Miele: But some critics question whether twins provide a fair representation of the entire population. Don’t you need other evidence?

Jensen: Yes, and further incontrovertible evidence comes from looking at the other side of the coin. Adoption studies allow us to compare genetically unrelated children who have been reared together from infancy against full siblings reared together. And adoption studies require fewer assumptions than any other method of estimating the effects of genetic factors and shared family environment on IQ. The IQ correlation between unrelated children reared together decreases with age, going from about 0.30 in early childhood to almost zero in late adolescence, showing that the effect on IQ of being reared together in the same family is virtually washed out by the time people reach maturity.

The Texas Adoption Project with 300 adoptees, conducted by a team of behavioral geneticists at the University of Texas, is the largest data bank of this kind and has the highest quality of data, with IQs of all family members. A path model analysis of these data, consisting of IQs for the mother, father, their biological offspring, and the adoptees, was recently performed by the Texas team when the adopted children had an average age of 17 years. The population value of the heritability derived from these data is 0.78, which is not significantly different from the heritability of 0.75 estimated from the correlation between MZ twins reared apart or even Sir Cyril Burt’s allegedly “cooked” heritability of 0.77! The strong agreement between the two most direct lines of evidence—identical twins reared apart and unrelated children reared together—provides the best estimate we now have of IQ heritability.

The most important and unarguable point in all of these studies is that no one has been able to explain the pattern of the various kinship correlations without recognizing the substantial effect of genetic factors. If it could have been done, it certainly would have been done by now, because many technically competent scientists have tried. Even if heredity turns out to be King Kong and not Godzilla, would that make you switch your bet to Bambi in the hypothetical stomping match?

Miele: Well, the Human Genome Project is in the process of trying to map every human gene. That should provide the most direct evidence imaginable. So far, the Project has identified the specific genes for various diseases, including mental and behavioral ones like Alzheimer’s. But no one has found a gene for intelligence. If the heritability estimates are accurate as you claim they are, shouldn’t finding the IQ genes be relatively easy? After all, your theory says that there are many genes that contribute to IQ. Why hasn’t anyone stumbled onto at least one of them?

Jensen: One doesn’t merely stumble onto these things. One has to search for them. But you’re wrong. At least four genes or DNA segments that affect IQ have been identified by behavior geneticist Robert Plomin of the Institute of Psychiatry of the University of London. And his investigation continues. These experiments have to be replicated at least two or three times to rule out chance findings, and the genes identified have held up in repeated studies.

The method Plomin uses is known as quantitative trait loci, or QTL. What he and his research team do is to get two groups of subjects, one group with average IQs and another group with very high IQs. Using blood samples from these two groups, they extract DNA and examine a strand of DNA from a particular chromosome (in this case, chromosome number 6) and search for a significant difference in the DNA between the average and high IQ groups. A significant difference in the DNA could be a marker of one of the genes that influence IQ. The research team then has to look at the same DNA in a new set of average and high IQ groups to see if the same significant difference in DNA shows up. To rule out any “chance” effect, you have to repeat the study with new groups. It is certainly not easy to do this research, as you seem to believe it should be. It is extremely laborious and painstaking, but is getting somewhat easier as the technology of molecular genetics develops more efficient methods of DNA analysis.

And because intelligence is polygenic, each gene contributes only a small part of the total variation in IQ. The first few genes discovered, for example, account for only about 3 or 4 percent of the total IQ variance. The genes with the largest effects will most likely be found first. The task of finding the next ones will probably become more difficult, because each one’s effect will likely be smaller than that of those found earlier in the search. From all the evidence of the high heritability of IQ, however, we know that genes are involved. But finding the specific genes is much like looking for needles in a haystack, even when you know for sure that there actually are needles in the haystack.

Miele: Then if it’s so difficult to look for the specific genes, why bother if we already know from heritability studies that IQ is partly genetic?

Jensen: For the same reason that geneticists look for the specific genes for, say, a particular form of cancer, or for a type of Alzheimer’s disease, or Huntington’s chorea, or Tay-Sachs disease, cystic fibrosis, muscular dystrophy, and many other genetic conditions. Identifying the gene or genes is the first step in uncovering the processes by which some individuals develop lower or higher IQs than others. Merely knowing that something is genetic doesn’t explain much of anything; it only tells us where to look for the explanation, or at least some part of it. A good example is a type of mental retardation known as phenylketonuria, or PKU, which we now know is caused by a double recessive gene. Possession of this particular gene was found to result in a failure to metabolize properly a certain protein. This faulty metabolism yields biochemical products that damage the growing brain, thereby retarding mental development. Eliminating this protein (phenylalanine) from the diet, in fact, usually allows mental growth to proceed fairly normally. We want to discover the chemical modus operandi for the most influential genes that are involved in human intelligence.

At the same time, neuroscientists are directly studying the brain structures and the neural and metabolic processes that underlie intelligence. For a complete understanding, we have to explore in both directions, from the genes and from the brain. Like digging a tunnel, you excavate from both ends. That’s how I see the advancement of our knowledge of the physical basis of intelligence as taking place.

Miele: Is there anything to be gained by more heritability studies of the Whites in North America and Europe? What about other groups, especially Blacks? Can heritability studies ever tell us anything about the cause of the Black-White difference in average IQ?

Jensen: By now, heritability studies of g in White populations have probably reached the point of diminishing returns. There have been a few studies of IQ heritability in the Black population and there seems to be no statistically significant difference from the White heritability of IQ. But the heritability within each group alone tells us virtually nothing about whether the average difference between the groups is heritable. If the group means differ markedly, and if the heritability of IQ within each group is very high, and if the environmental factors known to affect IQ do not differ very much between the groups, it would be surprising if the groups did not actually differ genetically to some extent. But such evidence by itself is insufficient to support any serious argument on this point. Other lines of evidence are needed for studying the causes of the observed average IQ difference between different racial populations. I have discussed this whole issue in considerable detail in my book The g Factor.

Miele: Then let’s take it up in the next chapter.

3NATURE, NURTURE, OR BOTH?

Can Heritability Cut Psychology’s Gordian Knot?

A Primer on Variance and Heritability

An Example

The Important Things to Remember About Variance and Heritability

Further Reading

3
NATURE,
NURTURE, OR BOTH?

Can Heritability
Cut Psychology’s Gordian Knot?

The Important Things to Remember
About Variance and Heritability