© Springer International Publishing AG, part of Springer Nature 2019
Natalia Kryvinska and Michal Greguš (eds.)Data-Centric Business and ApplicationsLecture Notes on Data Engineering and Communications Technologies20https://doi.org/10.1007/978-3-319-94117-2_4

Traffic Fluctuations Optimization for Telecommunication SDP Segment Based on Forecasting Using Ateb-Functions

Ivan Demydov1  , Ivanna Dronyuk1  , Olga Fedevych1   and Vasyl Romanchuk1  
(1)
Lviv Polytechnic National University, S. Bandera Street, 12, Lviv, Ukraine
 
 
Ivan Demydov (Corresponding author)
Email: ivan.demydov@gmail.com
 
Ivanna Dronyuk
Email: ivanna.m.droniuk@lpnu.ua
 
Olga Fedevych
Email: olha.fedevych@gmail.com
 
Vasyl Romanchuk
Email: romanchuk@lp.edu.ua

Abstract

This work proposes a network traffic prediction method based on a theory of differential equations with them solutions can be written as Ateb-functions. The proposed method first uses the hypothesis about cyclic nature of network traffic pulsations. Then, description of the traffic intensity fluctuations into the computer network builds a prediction model, as nonlinear oscillating system with single degree-of-freedom under the conditions of small-scale disturbances. From the simulation, the proposed prediction method in distinction from existing methods gives more qualitative solution. Thereafter, the obtained values of the predicted traffic intensity are used as one of the key indicators in solving the problem of optimal resource allocation in heterogeneous network platforms by correcting the metrics or priorities of traffic flows routing. Decisions taking on a basis the procedures for evaluating alternatives by mutually related and mutually controversial criteria using fuzzy logic approach with triangular fuzzy numbers aggregation.

Keywords

Traffic fluctuationsForecastingAteb-functionOptimization

1 Introduction

This research work contributes to the methods of forecasting and modeling of traffic flows in computer networks, which are widely used and developed to date, being in a state of constant elaboration, and are continuously implemented in the latest concepts such as IoE, XaaS cloud solutions for effective processing significant volumes of custom content and associated metadata, BigData, and more. The purpose of the study is to create information technology for monitoring and adaptive control of pulsating (non-stationary) traffic flows in computer networks by predicting load intensity and redistribution of node capacity in a given segment of a network service delivery platform.

In our understanding, which coincides with the classical definitions for packet switching technologies, the term “traffic” denotes the network load or amount of information, in other words, the number of packets transmitted over a specified time unit [1]. In turn, bandwidth is the limitation of traffic volumes, which exists depending on the software and hardware on a specific area of the telecommunication network [2].

Scientific research of heterogeneous network traffic shows that it’s nature is self-similar or fractal in fact [3]. We can postulate, that the methods used previously for the calculation and modeling of network systems and based on the use of Poisson arrivals theory do not provide a complete and accurate picture of what processes occur in the computer network of service delivery platform [4].

In addition, self-similar traffic has a special structure that is persisted when using multiple scaling. In implementing this approach, as a rule, there is a certain amount of intensity surges even at relatively low amounts of traffic. This phenomenon worsens the characteristics (increases latency, packets’ jitter) when passing such traffic through the nodes of computer network equipment. In practice, this is manifested in the fact that packets in the conditions of high speed of their transmission through a computer network, arrive at the node not separately, but rather large in volume groups, which can lead to their losses due to the limited volume of buffer memory of commutation equipment that was pre-calculated using classical techniques.

The described features of network traffic caused a large increase in the number of publications and scientific research on the methods of analysis, modeling, and prediction of self-similar traffic [1–4].

Traffic of a Gigabit Ethernet channel exhibits self-similar properties with a likely high value of the Hurst index, as shown in the research in [5]. Attention deserves time intervals during which the network is impacted by anthropogenic nature, because at that time there is a high probability of buffers overflow in the network nodes, which can lead to queues in the system and, consequently, a sharp deterioration in the quality of service for the whole range of existing services provided by the communication provider. It is also shown that the self-similar properties of traffic allow with a sufficient degree of credibility to predict the appearance of time intervals in the segment of the network platform where there is an overload due to the productivity of equipment and communication lines, which in turn makes it possible to construct a system with dynamic control of bandwidth reserves for specified traffic types [6]. So, work [5] confirms our view that traffic forecasting plays a significant role in the development of traffic management algorithms aimed at improving the quality of service. It should be noted that with the growth of volumes of info communication services, there is a shortage of network resources, throughput capacity of data transmission channels, which, as already mentioned above, affects the quality of services provided to users.

In the works [5, 7], the authors developed the computational schemes for forecasting traffic using three methods: the Boxes-Jenkins method, the derivative method and the modified Boxes-Jenkins method using splines. In [8], based on this approach, a method for forecasting self-similar traffic, which can be used for modeling data flows in packet networks, is proposed. The developed algorithm is based on the Boxes-Jenkins procedure. The results of the forecast obtained by this algorithm are based on a large number of data, the values of which more influence the result of the forecast, the closer this data in time to the moment of forecasting.

Based on the aggregated models using wavelet transformations [9], the forecasting of traffic has been realized considering statistical characteristics, as well as the properties of scaling invariance.

There is interesting and quite novel the method for traffic forecasting, presented in [10], based on a deep learning architecture and the Spatiotemporal Compressive Sensing method to extract the low-pass component of network traffic by adopted discrete wavelet transform, and then high-pass component, and obtain a predictor of network traffic.

Therefore, research on a certain topic has shown that in general methods for modeling and predicting the transmission of traffic in modern computer networks have not been sufficiently studied. This indicates the need to develop new models and methods for forecasting traffic to increase the efficiency of using computer network resources.

In addition, it is important that the task of controlling the workload of SDP is not only multicriteria, but often criteria that are chosen to solve its optimization component are mutually controversial, and the solutions themselves are subject to numerous limitations. Examples of such parameters are transmission delay, jitter, allocated bandwidth, current or predicted traffic intensity, economic performance, etc. Difficulty also occurs when an attempt is made to make an unambiguous decision in the context of additional technological constraints, for example when sensor networks with a limited energy budget are considered [11] or wireless networks with limited radio frequency and energy resources, ad hoc, etc. [12]. To effectively overcome such situations, several methods have been developed based on the use of the theory of fuzzy logic. In papers [13–17] aspects of load management in telecommunication networks are considered, in [18] the approach of fuzzy logic application in Random Early Detection is shown to equalize peak loads in systems of users’ load balancing and distribution. To a lesser extent, this direction also applies improvement of the technical efficiency indexes of sensor nets, that discussed in [11], and increasing the efficiency of routing in wireless network systems, delay tolerant nets [12, 19, 20, 21]. Despite this variety, all these works have not considering a simple and effective fuzzy-logic approach with TFN (Triangle Fuzzy Numbers) aggregation of parametric estimates based on a set of scales, which, for example, is used in [22, 23].

In the next subchapters of this work we discuss the principles of mathematical modeling to create a mechanism for predicting traffic fluctuations based on the theory of differential equations, whose solutions have the form of the Ateb-function. After that, the received values of the predicted intensity of traffic are used as one of the key indicators in solving the problem of optimal resource allocation in heterogeneous network platforms by correcting the metrics or priorities of traffic flows’ routing and making decisions based on the procedures for evaluating alternatives according to the given criteria using fuzzy logic on the basis of TFN.

2 Mathematical Model and Forecasting of Network Traffic Fluctuations

As a rule, the dynamics of changes in the network system’s workload is described, and, consequently, its forecasting is performed considering a certain volume of the known, or rather, fixed statistical information on the state of specific areas of the telecommunications platform. There are two structural approaches to predicting the traffic intensity. The first involves the distributed operation of some network data collection software, such as the Wireshark type. Second—centralized—involves the use of SDN-controller. Frequency of calculations of the traffic intensity is determined by the dynamics of load fluctuations since the nature of these fluctuations impacts on the accuracy of the forecasting. For public networks, these indicators are not very important, although they have a significant impact on service quality metrics. In networks with guaranteed quality of traffic flows servicing, load fluctuations have a detrimental effect on the stability of their operation (packet losses and delays). Centralized flow management allows us to control completely the load balancing process at the specified segment of the network platform, to form a complete matrix of predictive intensities of data channels utilization by their traffic-handling capacity.

Let us consider the fluctuations of traffic in a computer network as the function of time, as a nonlinear oscillating system with single degree-of-freedom in conditions of small disturbances. The simulation of the traffic intensity behaviour in the computer network represented by the function x(t) is performed by a simple differential equation with a small parameter ε in the form
$$\ddot{x} + a^{2} x^{n} = \varepsilon f\left( {x,\dot{x},t} \right),$$
(1)
where $$x\left( t \right)$$—is the number of packets in the network at time t; α—is the constant that determines the period of traffic fluctuation, $$f\left( {x,\dot{x},t} \right)$$—is an arbitrary analytic function used to simulate small deviations of traffic from the main component of oscillations, n—is the number that defines the degree of nonlinearity of the equation that affects the period of the main component of oscillations.
Under the following conditions on α and n $$\alpha \ne 0$$, $$n = \frac{{2k_{1} + 1}}{{2k_{2} + 1}},\,k_{1} ,k_{2} = 0,1,2 \ldots$$, is was proved [24], that the analytic solution of Eq. (1) is represented in the form of Ateb-functions. For tasks of traffic flows’ forecasting in the information network or telecommunication platform, it is important to choose the type of function f, in such a manner the peculiarities of the operation of given network system are taken into consideration. An approach that considers small disturbances in the form of periodic functions is appropriate for modeling a network with a smooth change in the intensity of traffic flow. However, the authors [25] decided to consider perturbation as a convolution of weighted delta functions. Such a description is more in line with the network, which has sharp changes in the intensity of traffic. Let’s consider the function f in the form
$$f\left( {x,\dot{x},t} \right) = \sum\limits_{i = 1}^{N} {a_{i} \delta \left( {t_{i} } \right)} ,$$
(2)
where N is the number of disturbances per time interval [0, T], $$a_{i}$$—disturbance range $$- A \le a_{i} \le A$$, A—the maximum disturbance range (is generated randomly), δ—Dirac delta function, $$t_{i}$$—the moment of time in which there is an i-th disturbance that is generated randomly.
To construct a solution, we first consider Eq. (1) without perturbation function
$$\ddot{x} + a^{2} x^{n} = 0.$$
(3)
If we write the differential equation of the second order (3) in the form of a system of differential equations of the first order, considering the replacement of the variables $$y = \dot{x}$$, then the differential equation of the second order (1) is transformed into the following system of differential equations of the first order:
$$\left\{ {\begin{array}{*{20}l} {\frac{dx}{dt} - y = 0} \hfill \\ {\frac{dy}{dt} + \alpha^{2} x^{n} = 0} \hfill \\ \end{array} } \right.,$$
(4)
and the solution (4) is represented by the periodic Ateb-functions in the following form
$$\left\{ {\begin{array}{*{20}l} {x = aCa\left( {n,1,\varphi } \right)} \hfill \\ {y = a^{{\frac{1 + n}{2}}} hSa\left( {1,n,\varphi } \right)} \hfill \\ \end{array} } \right.,$$
(5)
where a—an amplitude of intensity oscillations, $$Ca\left( {n,1,\varphi } \right),\;Sa\left( {n,1,\varphi } \right)$$—Ateb-cosine and Ateb-sine, respectively, $$h^{2} = \frac{{2a^{2} }}{1 + n}$$. The variable φ is corresponding to the time t by equation of the form
$$\varphi = \frac{{a^{{\frac{n - 1}{2}}} }}{L}t + \varphi_{0} ,$$
(6)
where L is some constant, $$\varphi_{0}$$—the initial phase of oscillations, which are determined from the initial conditions for the Eq. (3).
The following system of equations expresses periodic conditions:
$$\left\{ {\begin{array}{*{20}l} {Ca\left( {n,1,\varphi + 2\Pi } \right) = Ca\left( {n,1,\varphi } \right)} \hfill \\ {Sa\left( {1,n,\varphi + 2\Pi } \right) = Sa\left( {1,n,\varphi } \right)} \hfill \\ \end{array} } \right.,$$
(7)
where Π is half-period of Ateb-function. When we put the expressions (5) and (6) in Eq. (4) and consider condition (7), we obtain the following expression for calculating the constant L in formula (6):
$$L = \frac{{2B\left( {0.5,\frac{1}{1 + n}} \right)}}{{\Pi \left( {1 + n} \right)h}}.$$
(8)
In expression (8) B(x, y) defines the full Beta-function with arguments x = 0.5, y = 1/1 + n. Considering formula (6) and expression $$Ca\left( {n,1,\varphi } \right)^{m + 1} + Sa\left( {1,n,\varphi } \right)^{2} = 1$$, we receiving resulting formula to calculate the half-period of the Ateb-function
$$\Pi \left( {n,1} \right) = B\left( {0.5,\frac{1}{1 + n}} \right).$$
(9)
Let us consider the initial conditions for the system of differential Eqs. (4). In [26], these initial conditions for the differential Eq. (1) are considered as follows
$$x\left( 0 \right) = 0,\,\dot{x}\left( 0 \right) = const,$$
(10)
when $$n = \frac{1}{2k + 1}$$ and $$k \to \infty$$. Such initial conditions cannot be used to simulate the intensity of traffic flows. We assume that the values of traffic flows and changes in such traffic values are constantly determined at the time t  = 0. According to these assumptions, we determine the initial conditions as
$$x\left( 0 \right) = c_{1} ,\,\dot{x}\left( 0 \right) = c_{2} ,$$
(11)
where c1 determines the initial traffic and c1 ≠ 0, c2 determines the change of initial traffic and can be zero at the initial time moment t  = 0. Considering, that $$Ca\left( {n,1,0} \right) = 1$$ and $$Sa\left( {1,n,0} \right) = 0$$ and Eq. (5) we obtain from the initial conditions (11) that c1  =  a i c2  = 0.
We use the asymptotic method for constructing a solution of Eq. (1) based on (5). The asymptotic method builds a solution in the form of a numerical series with a small parameter ε
$$x\left( t \right) = \sum\limits_{i = 1}^{\infty } {\varepsilon^{i} x_{i} \left( t \right)} .$$
(12)
For numerical simulations, we must discard terms of series that contain ε by in order of magnitude more than M. Therefore, we obtain a solution with the accuracy of the order $$\varepsilon^{M + 1}$$. We will find solutions in the form of series for a small parameter ε, as follows
$$x\left( t \right) = \sum\limits_{i = 1}^{M} {\varepsilon^{i} x_{i} \left( t \right)} .$$
(13)
We substitute a numeric series (13) into the left part of (1), and after that expressions with the same order of small parameter ε were equated with each other. Now consider the Eq. (1), which is transformed into a system of differential equations with variables (just as done in (3) in (4)) of the form
$$\left\{ {\begin{array}{*{20}l} {\frac{dx}{dt} - y = 0} \hfill \\ {\frac{dy}{dt} + \alpha^{2} x^{n} = \varepsilon f\left( {t,x,y} \right)} \hfill \\ \end{array} } \right..$$
(14)
The degrees of a small parameter ε represent the asymptotic approximation. To create the first approximation in (13) according to the first order of ε (M  = 1 in the formula (13)), we make a replacement of the variables by type
$$x = \xi + \varepsilon f\left( {t,\xi ,\zeta } \right),\;y = \zeta = \dot{x}.$$
(15)
and equate the coefficients at the same degrees of ε, and, we discard the terms of the higher order relative to ε. As shown in [27], the variables ξ, ζ are calculated with respect to the solution without disturbance (5), can be taken as an improved first approximation of solutions (14) and (15).

On the basis of the developed mathematical model, a new method was proposed for simulating the intensity of traffic flows in info communication network systems. The basic hypothesis is that the nature of network traffic has a periodic nature. In this case, the simulation of the daily cycles of periodicity was carried out.

The first step was to simulate the main traffic trend. However, this approach does not consider the sharp fluctuations in traffic. Therefore, it was proposed to use the equation to simulate and predict the behavior of the intensity of traffic flows in a network platform, namely, use differential equations describing nonlinear oscillating systems with single degree-of-freedom and with small disturbances. It is assumed that the main periodic component simulates the daily volatility of traffic in the network, while the deviation of traffic from the main trend is modeled using a delta-function with a small parameter. For the solution of differential equations with small parameter, the asymptotic method of Bogolyubov-Mitropolskiy was used [28].

Figure 1 presents the results of application of the developed software complex, within the framework of the implemented new method of monitoring and forecasting the intensity of traffic flows. On their basis, it is suggested to carry out a redistribution of the load on a computer network segment, for example, using a modified Dijkstra algorithm applying heuristics or by estimating and prioritizing routes in the process of multi-path routing based on the theory of fuzzy logic.
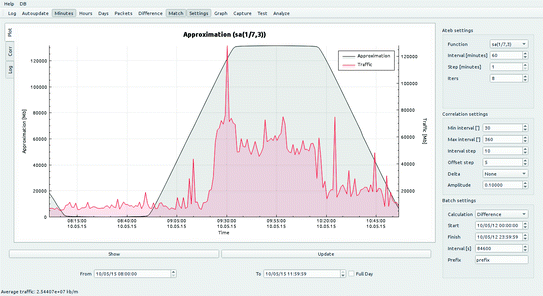
../images/462031_1_En_4_Chapter/462031_1_En_4_Fig1_HTML.gif
Fig. 1

The graphical comparison of traffic intensity and scalable predictive values based on the Ateb-function with parameters m = 1/7, n = 3

On Figs. 1 and 2 are shown samples of network traffic intensity profiles collected at the Department of Automated Control Systems of the Lviv Polytechnic National University, obtained from 20 working computers roughly enrolled to BigData processing in the local computing cluster from 8:30 to 17:30, as well as 4 computers loaded from 8:30 to 21:00 and 32 workstations enabled and working from 8:30 to 16:00.
../images/462031_1_En_4_Chapter/462031_1_En_4_Fig2_HTML.gif
Fig. 2

The graphical comparison of the traffic intensity in prediction after the application of the normal distribution of the delta function for the Ateb-function with parameters m = 1/5, n = 1

Figure 1 shows a sample of traffic profile (red line), and a predicted forecast (black). To calculate the predicted traffic values, the Ateb-function was selected with parameters m = 1/7, n = 3. Figure 2 shows the results of the normal distribution of the delta function application for the Ateb-function with the parameters m = 1/5, n = 1 to improve the process of traffic intensity values forecasting according to the developed method.

To improve the characteristics of the forecast, the mechanism of embedding of delta functions was additionally introduced. The graph is redrawn automatically. The results of the program operation in this case are presented on Fig. 2.

From Figs. 1 and 2 it should be concluded that it is possible to achieve a rather qualitative forecasting of the profile form of the traffic intensity, particularly the nature of emissions, even with small volumes of data on its previous values. The prediction accuracy, as well as the methods for raising it, are part of future authors’ research plans. At present, in [26] authors found that it is possible to achieve correlation between predicted and real (exemplary) traffic profiles at the level of 97–99% when performing short-term forecasting (for a period of 5–10 min), with medium-term forecasting—85 to 88% (per the term up to 1 day), with the worst recorded result not less than 75%. The results contributed show an improvement with respect to the derivative method up to 30% [7].

3 Approach to Correction of Routing Metric and Priorities Based on the Use of Fuzzy Logic Theory with Triangle Fuzzy Numbers

Optimization of the processes of redistribution (load balancing) between different routes in network platforms can be based on a certain set of criteria describing the quality of service (QoS): network latency, jitter, packet loss indexes (PER), network throughput (which is obtained on the basis of load intensity forecasting); QoE indicators; the priority of user servicing, the speed of their movement, the type of service, and for the case of mobile radio access systems—the signal level of the stations of each particular access network [29]. The combination of these criteria in the process of operation of the heterogeneous service delivery platform by some algorithms can significantly affect the quality of network services for end users and their level of satisfaction, and also the technical and economic efficiency of the distribution of network resources.

The theory of fuzzy sets is a means of solving tasks for the aggregation of ambiguous (ambivalent), subjective and fuzzy evaluation judgments about the state of some partial parameter or metric (metric), which directly affects the optimal choice or priority of the route, which is especially relevant for the case multi-path routing, that is, the existence of several alternative paths of data transmission.

Fuzzy sets, unlike the classical set theory, can divide the results on a scale corresponding to linguistic terms, and this can also be used for further decision-making by experts or an expert system. Using this approach to construct a mathematical model of the processes of assigning network resources, it (the approach) becomes quantitative, in contrast to existing subjective evaluation methods. At the same time, it can be relatively simple and algorithmically automated.

The scheme for calculating the criteria for the main types of network traffic of a heterogeneous telecommunications platform is presented on Fig. 3. Thus, it is proposed to divide all parametric criteria into two groups: QoS-dependent and those that depend directly on the properties of the radio interface (for the case of the wireless network access system analysis performing). The first group traditionally relates delay, jitter, packet loss ratio (PLR), network platform bandwidth, and, accordingly, to the second—predicted load intensity, relative cost of network resources usage, security level, for wireless telecommunications access platform—users’ mobility level [km/h] (velocity), signal strength (RSS, [dBm]) (see Fig. 3; Table 1).
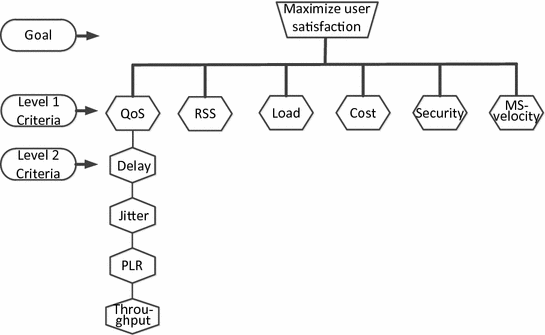
../images/462031_1_En_4_Chapter/462031_1_En_4_Fig3_HTML.gif
Fig. 3

A set of criteria for deciding on the initialization of the process of resource redistribution/prioritization of routes

Table 1

Estimates of criteria parameters of network systems for initiating the process of resource redistribution/giving priority to routes on the Likert scale

Scale

1

2

3

4

5

Min/max values

Predicted workload (%)

70–100

50–70

40–50

30–40

0–30

0–100

Cost

1–2

2–3

3–4

4–8

8–10

1–10

Security

1–2

2–4

4–6

6–8

8–10

1–10

Velocity (km/h)

<120

80–120

60–80

40–60

0–40

0–160

Delay (ms)

<300

200–300

100–200

50–100

10–50

10–500

Jitter (ms)

<30

20–30

10–20

5–10

1–5

10–30

Packet loss ratio (PLR) (%)

<8

6–8

4–6

3–4

1–3

1–8

Network platform band-width (Mbps)

<0/1

0.1–10

1–50

50–100

100–200

0/1–200

RSS (dBm)

<−110

−100 to −110

−90 to −100

−75 to −90

−55 to −75

−110 to −55

After preparing the parameters for computing to decide on the priorities for the routes (their areas selected on the basis of the next hop), we introduce the scale of the values of each criterion [for their presentation in the format of triangular fuzzy numbers (TFN)] regarding the initiation of such resource redistribution, and put it in line with the Likert scale [1—“cannot be applied” (0,0,0.25), 2—“can be used” (0.0.25.0.75), 3—“average”, (0.25, 0.5, 0.75), 4—“highly likely to be used” (0.5.0.75.1), 5—“to be applied” (0.75.0.75.1)], taking into account the estimates of Table 1.

Accordingly, in the process of fuzzification, the calculation of triangular fuzzy numbers (Triangle Fuzzy Number) $$\tilde{Q}_{mn}$$ for the aggregated estimation of selected sections (alternatives) of the route to some platform network node. The latter is performed in accordance with the values of the criteria of the service quality group from Table 1 which are additionally multiplied with normalized weighting factors, that is, according to the estimates of the values of the criteria parameters for making a decision on the redistribution of network resources on the scale given in Table 1. As a matter of fact, the re-routing procedure itself (or changing the priorities of alternative route paths) may indeed lead to changes in QoS indices for the served user.
$$\tilde{Q}_{mn} = \left( {q_{1} ,q_{2} ,q_{3} } \right)_{mn} = \sum\limits_{i = 1}^{4} {\left( {W_{imn} \times \tilde{L}_{imn} } \right)}$$
(16)
$$q_{{j_{mn} }} = \sum\limits_{i = 1}^{4} {\left( {W_{imn} \times l_{ijmn} } \right)} ,\quad \left( {j = 1,2,3;\,n = 1,2} \right),$$
(17)
where $$q_{1} ,q_{2} ,q_{3}$$ is the lower level of the generalized estimate $$\tilde{Q}$$, its main value and the upper level, respectively, $$\tilde{L}_{imn} = \left( {l_{i1} ,l_{i2} ,l_{i3} } \right)_{mn}$$ is a triangular fuzzy number that characterizes the parameter of the network node according to the i-th criterion, and the node itself belongs to a heterogeneous network platform with serial number m and uses n-th access technology [22]. Here $$l_{i1} ,l_{i2} ,l_{i3}$$ are the lower level of the linguistic variable, its main value, and the upper level, according to the format of triangular fuzzy numbers (Triangular Fuzzy Number) [23].

At the same time and in the same way (16–17), a generalized assessment of priority for a selected (alternative) route section to an access node of network platform is calculated $$\tilde{P}_{mn}$$, which is calculated in accordance with the technology which was applied in this section and partial estimates of the group of technical (technological group) parameters that based on the interpretation of input data (see Table 1), in particular the predicted load intensity for defined part of the network platform. This score, together with the value of expression (16), will qualitatively characterize a particular route or its sections, which for example, was laid down to a specific node of the network access platform.

The aggregated qualitative assessment of the priority of a route to a given network node can be defined as follows
$$\begin{aligned} \tilde{R}_{mn} &amp; = \left( {r_{1mn} ,r_{2mn} ,r_{3mn} } \right) = 1/2 \times \left( {\tilde{Q}_{mn} + \tilde{P}_{mn} } \right) \\ &amp; = 1/2 \times \left( {q_{1mn} + p_{1mn} ,q_{2mn} + p_{2mn} ,q_{3mn} + p_{2mn} } \right). \\ \end{aligned}$$
(18)
Finally, we will make a defuzzification of the received fuzzy (triangular) number (18) in accordance with the method proposed in [23] for obtaining an aggregated quantitative estimate:
$$R_{mn} = 1/3 \times \sum\limits_{t = 1}^{3} {r_{tmn} } .$$
(19)
In [22], an example of the implementation of fuzzification and defuzzification procedures into some network platform is presented to optimize the distribution of its resources and the execution of vertical handover through mathematical and probabilistic statistical simulation (see Fig. 4).
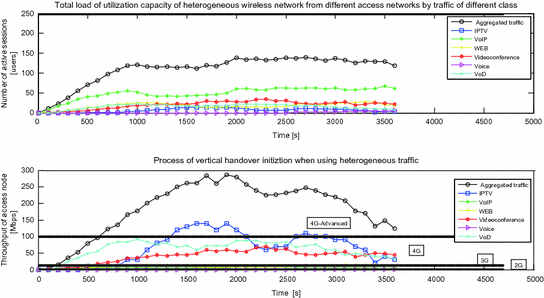
../images/462031_1_En_4_Chapter/462031_1_En_4_Fig4_HTML.gif
Fig. 4

The load intensities on a heterogeneous network platform from various network access systems and the threshold for initiating an intelligent vertical handover

For greater clarity, we assume that we have 6 alternative route sections (Section 1–Section 6) under conditions of the need to route a path from a user of a heterogeneous network access platform, when using GSM and LTE technologies to organize its radio interfaces. We need to choose a better alternative (in fact—to select the “last mile” route) under the current operating conditions, that is, when the system has some set of parameters, see Table 2. The choice will be made in accordance with Fig. 3 and scales of Table 1.
Table 2

Estimation results based on fuzzy sets (triangular fuzzy numbers) for network access nodes and their defuzzification (Rmn)

 

Section 1 BS1 (GSM)$$1/2 \times \left( {\tilde{Q}_{mn} + \tilde{P}_{mn} } \right)$$ $$\left( {\tilde{R}_{mn} } \right)$$

Section 2 BS2 (GSM) $$1/2 \times \left( {\tilde{Q}_{mn} + \tilde{P}_{mn} } \right)$$ $$\left( {\tilde{R}_{mn} } \right)$$

Section 3

Section 3 BS3 (GSM) $$1/2 \times \left( {\tilde{Q}_{mn} + \tilde{P}_{mn} } \right)$$$$\left( {\tilde{R}_{mn} } \right)$$

Jitter

(0,2; 0,005; 0,005)

(0,2; 0,005; 0,005)

(0,105; 0,005; 0,005)

PLR

(0,04; 0,053; 0,03)

(0,04; 0,053; 0,03)

(0,008; 0,053; 0,003)

Bandwidth

(0,15; 0,095; 0,075)

(0,1; 0,0095; 0,06)

(0,01075;0,0057; 0,1750)

Delay

(0,105; 0,04)

(0,05; 0,105; 0,04)

(0,1; 0,105; 0,0055)

Cost

(0,0025; 0,0125; 0,01)

(0,0025; 0,0125; 0,01)

(0,006; 0,011; 0,001)

Security level

(0,0225; 0,0525; 0,15)

(0,0225; 0,0525; 0,07)

(0,00375;0,05375; 0,15375)

User velocity

(0,032; 0,017; 0,12

(0,032; 0,017; 0,02)

(0,0052; 0,012; 0,12)

RSS

(0,0125; 0,0875; 0,125)

(0,0625; 0,0375; 0,052)

(0,125;0,00475; 0,0475)

Predicted intensity of workload

(0,00525; 0,00525; 0,00525)

(0,00525; 0,00525; 0,00525)

(0,00525; 0,00525;0,00525)

Fuzzified estimate $$\left( {\tilde{R}_{mn} } \right)$$

(0,51475; 0,43275; 0,56025)

(0,51475; 0,29725; 0,29275)

(0,36895; 0,2555; 0,516)

Result of de-fuzzification $$R_{mn}$$

0,502583333

0,36825

0,38015

 

Section 4 BS1 (LTE) $$1/2 \times \left( {\tilde{Q}_{mn} + \tilde{P}_{mn} } \right)$$ $$\left( {\tilde{R}_{mn} } \right)$$

Section 5 BS2 (LTE) (conditionally best alternative route) $$1/2 \times \left( {\tilde{Q}_{mn} + \tilde{P}_{mn} } \right)$$ $$\left( {\tilde{R}_{mn} } \right)$$

Section 6 BS3 (LTE) $$1/2 \times \left( {\tilde{Q}_{mn} + \tilde{P}_{mn} } \right)$$ $$\left( {\tilde{R}_{mn} } \right)$$

Jitter

(0,15; 0,005; 0,005)

(0,2; 0,005; 0,005

(0,105; 0,005; 0,005)

PLR

(0,04; 0,053; 0,023)

(0,04; 0,053; 0,03)

(0,04; 0,053; 0,008)

Bandwidth

(0,25; 0,0095; 0,175)

(0,25; 0,195; 0,175)

(0,01; 0,005; 0,175)

Delay

(0,1; 0,105; 0,0055)

(0,1; 0,105; 0,04

(0,1; 0,105; 0,0055)

Cost

(0,006; 0,0225; 0,001)

(0,0051; 0,0225; 0,01)

(0,006; 0,006; 0,001)

Security level

(0,0325; 0,075; 0,15)

(0,0325; 0,0525; 0,25)

(0,0375; 0,0525; 0,15)

User velocity

(0,032; 0,012; 0,12)

(0,032; 0,017; 0,12)

(0,032; 0,012; 0,12)

RSS

(0,1025; 0,2375; 0,225)

(0,125; 0,2375; 0,225)

(0,125; 0,2375; 0,225)

Predicted intensity of workload

(0,00525; 0,00525; 0,00525)

(0,00525; 0,00525; 0,00525)

(0,00525; 0,00525; 0,00525)

Fuzzified estimate $$\left( {\tilde{R}_{mn} } \right)$$

(0,71825; 0,52475; 0,70975)

(0,78985; 0,69275; 0,86025)

(0,46075; 0,48125; 0,69475)

Result of de-fuzzification $$R_{mn}$$

0,6509166

0,78095 (conditionally best alternative route)

0,545583333

The most optimal result for establishing the highest priority of the route segment for a particular user and, accordingly, implementing the redistribution of the network resources of the heterogeneous network platform was obtained for section 5 of the route, that is, the access node BS2 (network subsystem of LTE technology) (shown in Fig. 5, according to Table 2). The result for the route section 4, that is, the access node BS1 (also the network subsystem of the LTE technology), is lower, although, according to the membership function, belongs to the same linguistic term “High” (see Fig. 5). Thus, the theory of fuzzy sets demonstrates the quantitative difference between the qualitatively homogeneous solutions of the optimization problem of the converged resources distribution at network-dependent levels of heterogeneous distributed network platforms, which is useful, in particular, for solving the problems of multi-path routing.
../images/462031_1_En_4_Chapter/462031_1_En_4_Fig5_HTML.gif
Fig. 5

Determination of the optimal alternative when selecting the route section from the user of the heterogeneous network access system using the Likert scale for the set of criteria values (Table 1)

4 Conclusion

The work proposes a combination of several approaches to increase the effectiveness of traffic management and the adoption of optimal solutions. Namely, the introduction of the Ateb-prognostication method for constructing a traffic matrix in the segment of the network system and further aggregated estimation of the chosen sections (alternative variants) of the route to some network node of the platform based on the theory of fuzzy sets is proposed. The result is an improvement in the method of routing the traffic of data flows in the service delivery platform segment, which consists in predicting the intensity of the pulsations of this traffic on the set of existing routes, providing the correction of the data transmission route and possible reducing the load of the buffers of the network equipment. And, accordingly, the delays that occur when the traffic ripples. In this way, the quality of the computer network platform operation increases, in particular, when the user content is transmitted according to the criteria of the QoS group.

To solve the problem of accepting the optimal (according to the criteria of the QoS group and other technological criteria) solution to the routing procedure while servicing users of network service delivery platforms, a centralized method for managing the priority of routes or their sections was proposed (could also be applied for “next hop” routing type). The proposed approach avoids ambiguity in the interpretation of ambiguous, fuzzy-evaluated and subjective judgments in the process of multi-criteria optimization of the network resources utilization, especially in conditions of significant load intensity in the network platform using the SDN controller. To study the processes of real heterogeneous network systems operation in the conditions of users’ high velocity authors have been developed a software simulation model, which, in turn, implements the contributed mathematical model of the decision-making process for mentioned procedures based on the use of fuzzy logic methods. This allows us to configure a large number of simulation parameters using Ateb-prognostication, auxiliary mathematical models, for example—to describe and predict the movement (mobility) of users on heterogeneous network platforms. Obviously, the choice of the optimal route or its alternative sections at such platforms based on the solving of the multicriteria optimization task of making a decision on the redistribution of network resources is non-trivial, since it is affected by several dynamic and mutually interrelated (often contradictory) factors. Thus, their aggregation is effective in accordance with the approaches proposed in this work.

Acknowledgements

The authors acknowledge the support from the Ministry for Education and Science of Ukraine and from the joint Ukrainian-Austrian R&D project titled “Traffic and telecommunication networks modelling” (0117U001612).