

Several years ago I was on holiday with my family and a group of friends in France. We were staying in an idyllic country farmhouse in the Limousin region of the Massif Central, one of the most sparsely populated areas of the country. Late one evening, with the children asleep, we adults were sitting outside enjoying a last glass or three of the local red wine, looking up at the clear, sparkling night sky and commenting on how France is big enough for one still to find uninhabited swathes of countryside where the light pollution is low, and how unaccustomed we were, living in the densely populated southeast of England, to being able to see so many stars overhead. Most impressive of all was a large streak of faint, diffuse light smeared across the sky, looking like a wispy cloud.
But a cloud would have obscured the distant stars in our line of sight from view—and we could clearly see just as many stars overlaying this wispy streak as elsewhere in the sky. It seemed as though it had to be something behind the distant stars. Being the resident scientist in the group, I was eager to point out that what we were seeing was the central disk of our Milky Way galaxy edge on, and that this patch of light was vastly farther away than all the individual stars we could see. Several of my friends admitted, to my astonishment, that they had never seen it before, and were fascinated to hear me explain that it consisted of the billions of stars that make up the bulk of our galaxy and are too far away and too faint for us to see as individual pinpricks of light.
Of course, not every one of the pinpricks of light we do see in the night sky is a star. The brightest objects of all (discounting the Moon, of course) are our planetary neighbors Venus, Jupiter, and Mars. These glow because they reflect the light of the Sun, which is hidden from our view on the other side of the Earth during the night. The nearest stars to us beyond our solar system are several light-years away. Remember that, confusingly, a light-year is a unit of distance, not time. It is the distance light travels in one year, and comes in at a cool 10 trillion kilometers. To put this into a context that I hope is easier to grasp, the 150 million kilometers that separate us from the Sun amount to just 0.000016 of a light-year. In fact, it is more sensible to say that the distance between the Earth and the sun is 8.3 light-minutes, since that is how long (just over eight minutes) it takes light to cover the distance.
The next nearest star to us, after the Sun, is Proxima Centauri at just over four light-years away. But it is not the brightest star in the sky; that title goes to Sirius, which is twice as far away. Only the Moon, Jupiter, and Venus are constantly brighter than Sirius, which can be seen wherever you are on the planet, unless you live several hundred miles north of the Arctic Circle. It forms, along with Betelgeuse and Procyon, one of the three vertices of the Winter Triangle of stars as viewed from the Northern Hemisphere. To find it, locate the three stars that make up the belt of Orion and follow them downward. It’s hard to miss.
Other bright stars include the very distant but massive Rigel, a blue supergiant, seventy-eight times as big as the Sun and 85,000 times as bright, making it the most luminous star in our local region of the galaxy. We don’t see it shine as brightly as other stars in the sky, like Sirius, because it is so far away (between 700 and 900 light-years from the Earth). At about the same distance away, but even bigger than Rigel, is the slightly less luminous red supergiant, Betelgeuse. This great star is 13,000 times as bright as the Sun and a thousand times as big—so huge that, if it were to replace the Sun at the center of our solar system, it would engulf the orbits of Mercury, Venus, the Earth, Mars, and Jupiter!
Once astronomers began to use telescopes, enabling them to see farther out into the heavens than they ever could with the naked eye, they realized that stars are not distributed evenly throughout the Universe, but are instead clustered together in galaxies, each of which is like an immense star city; and that these galaxies are separated by unimaginably vast empty expanses of space. All the stars we can see in the sky (including Sirius, Rigel, and Betelgeuse) are part of our own galaxy, the Milky Way. Indeed, they are all in our local tiny neighborhood of the Milky Way.
Under perfect conditions (right part of the world, right time of year) we should be able to make out several thousand stars with the naked eye, and hundreds of thousands with a decent small telescope. Yet even this figure is a tiny fraction (less than 1 percent) of all the stars in the Milky Way, which contains between 200 and 400 billion stars—that’s around fifty stars for every human alive in the world today.
This is why the disk of the Milky Way appears as a continuous patch of faint light across the night sky. The galactic core is about 25,000 light-years from the Earth, while the galaxy as a whole has a diameter of 100,000 light-years. Such distances mean that individual stars are far too faint to resolve into clearly defined points of light, so that all we can see is the cumulative light from billions of them together.
The stars are not uniformly spread throughout the galaxy. Unlike our Sun, which sits alone, most stars come in pairs or groups orbiting each other. Some young stars hang together in their hundreds in loose open clumps, while larger groups, thousands strong, can be found in what are known as globular clusters.
We certainly cannot distinguish individual stars in other galaxies. In fact, it is almost impossible to see other galaxies at all without the help of powerful telescopes. Even our nearest neighbor galaxies, Andromeda and the Magellanic Clouds, are barely visible to the naked eye, appearing only as diffuse patches of very faint light.
The Andromeda galaxy, which is a little bigger than ours, is 2 million light-years away. If we were to shrink the Milky Way down to the size of the Earth, then Andromeda would be as far away as the Moon. Andromeda contains about 500 billion (or half a trillion) stars. I recall the thrill of first seeing it through a telescope, appearing as a faint fuzzy spiral. What hit me was the fact that I was seeing Andromeda not as it actually is now, but as it existed 2 million years ago. It was the light that had left it then, long before humans existed on Earth, that was only now entering my eye, thus completing its long journey. I felt weirdly privileged to have been there at that very moment to capture those photons of light as they made contact with my retina, triggering electrical signals that were sent to the neurons in my brain, making me conscious of what I was seeing.
Physicists often tend to think in this strange way.
Not only do stars form clusters within galaxies, galaxies themselves also group together in clusters. Our galaxy is one of about forty that together are known as the Local Group and also include the Large and Small Magellanic Clouds and Andromeda. Astronomical measurements have now reached such a degree of precision and sophistication, with ever-more powerful telescopes being built, allowing us to probe ever deeper into space, that we now know that galaxy clusters are themselves grouped together into what are known as superclusters. Our Local Group is in fact part of the Local Supercluster. How far out do the contents of our universe extend? Is it, in fact, infinite? We simply do not know. But the question has plagued astronomers for centuries and leads to our next paradox.
As we stare out into the night sky, we may ask a very profound question:
Why does it get dark at night?
You might think that this is a rather trivial question. After all, even a child knows that night falls when the Sun “sets” below the horizon, and that since there is nothing else in the night sky anywhere near as bright as the Sun we have to make do with the feeble reflected light from the Moon and the even more feeble light emanating from the distant planets and stars.
And yet it turns out this question is far more significant than it first appears. Indeed, astronomers puzzled over it for hundreds of years before they found the correct answer. It is known today as Olbers’ Paradox.
Here, then, is the problem. We have good reason to believe that even if the Universe is not infinite in size (and it may well be), it is so enormous that to all intents and purposes it goes on forever. Thus, in every direction we care to look out into space, we should see a star, and the sky should be even brighter than it normally becomes during the day; in fact, it should be so bright, all the time, that it should not even matter whether it is day or night according to our Sun.
Let’s look at it another way. Imagine that you are standing in the middle of a very large forest—so large, in fact, that you can assume it extends to infinity in all directions. Now try shooting an arrow horizontally in any direction. In this idealized situation the arrow must be allowed to keep on going in a straight line without ever dipping down to the ground until it hits a tree trunk. Even if it misses all the closer trees, the arrow must eventually hit one. Since the forest is infinite, there will always be a tree in the flight path of the arrow, however far away that tree may be.
Now imagine that our universe goes on forever with an infinity of stars evenly distributed throughout it. The light that reaches us from these stars is like the example of the arrow, but in reverse. For no matter where we look in the sky, we should always see a star in our line of sight. So there would not be any gaps where we do not see a star, and the whole sky should be as bright as the surface of the Sun, all the time.
When you first consider this dilemma, you might raise two points, both of which featured in my introduction to this paradox. First, you might ask: wouldn’t very distant stars simply be too faint for us to see? And second: stars are not evenly spread out in the sky, are they? Aren’t they bunched up in clusters, and those clusters grouped into galaxies? It turns out neither of these issues matters. In response to the first point, while it is true that more distant stars appear dimmer than closer ones, the corresponding patch of sky they are in would encompass a much larger volume since it is farther away, and so would contain more stars. A relatively simple bit of geometry that I shall discuss a little later on in this chapter shows that these two effects balance out exactly: for any given patch of sky, the fewer, nearer stars would have a total brightness equal to the more numerous, more distant stars. On the second point, it is indeed true that stars are not spread out evenly but are collected together in galaxies, like autumn leaves swept into neat piles. Beyond our own galaxy, the spots of light we see through telescopes are entire galaxies. So the argument is the same, only now we consider galaxies rather than individual stars: surely the night sky should be as bright as an average galaxy—not quite as bright as the surface of a star, but still blinding.
Well, no. And, as we will see, the reason why not turns out to be one of the most profound truths about our universe that we have ever discovered. But in order to resolve the paradox satisfactorily, we must first see how it evolved through history.
Given how long astronomers have been aware of this paradox, it is somewhat surprising that it was as recently as the 1950S that it was attributed to, and named after, Heinrich Wilhelm Olbers, a nineteenth-century physician and amateur astronomer from Bremen in Germany. In fact, few astronomers even seemed interested in it until then.
In 1952 the great Anglo-Austrian cosmologist Hermann Bondi published an influential textbook in which the term “Olbers’ Paradox” was coined for the first time. But as we shall see, the attribution was misplaced, for Olbers was not the first to pose the problem, nor was his contribution to its resolution particularly original or enlightening. A century before him Edmond Halley had already stated it, and a century before him Johannes Kepler had posed it in 1610. And even he wasn’t the first to record it: for that, we have to go back to 1576 and the very first English translation of De revolutionibus, the great work of Copernicus, written a few decades earlier.
Any account of the history of astronomy begins with the same few key individuals in the leading roles. First up is Ptolemy, the second-century Greek who, despite writing one of the most important scientific textbooks in history (known as the Almagest), believed erroneously that the Sun revolved around the Earth. He developed a model of the Universe with the Earth at its center that held sway among astronomers the world over for a thousand years and more. Then there was Copernicus, the Polish genius of the sixteenth century who, in overthrowing Ptolemy’s “geocentric” idea and switching the roles of Sun and Earth, is regarded as the father of modern astronomy. And we must not forget Galileo, the first astronomer to point a telescope at the sky, in 1609, and in doing so to prove that Copernicus’ “heliocentric” model was right: the Earth does indeed orbit the Sun, as do the other planets.
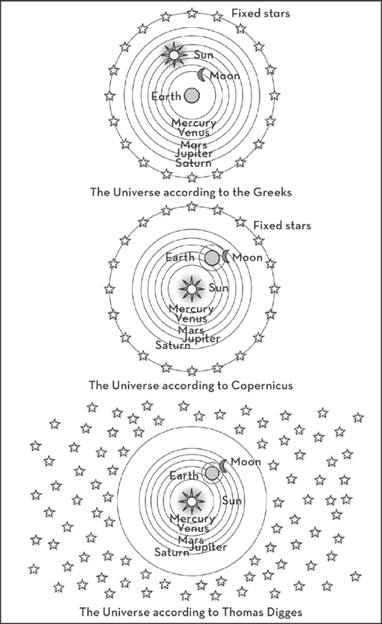
But Copernicus was not completely right. Though he was correct in removing the Earth from its privileged position at the very center of the Universe, he was wrong in simply replacing it with the Sun, believing that the solar system was the Universe. In De revolutionibus, regarded as one of the texts responsible for the scientific revolution in Europe, he shows an iconic diagram of the solar system. In it, the Earth is shown correctly to be the third planet out after Mercury and Venus, with the Moon the only object in the heavens to truly orbit it; then come Mars, Jupiter, and Saturn. All correct so far (the outer planets beyond Saturn were yet to be discovered)—but then, at this point, Copernicus did something very interesting. He placed all the stars in a fixed outer orbit around the Sun. So he has the Sun truly at the center of the whole universe, not just its system of planets.
We, of course, know now that our Sun does not have this special position. We know that in fact the Sun sits on an outer arm of an average spiral galaxy in a nondescript part of the Universe. We know, with the benefit of centuries of ever more comprehensive and accurate astronomical data, leading to our current understanding in modern cosmology, that the Universe has no center at all, and may indeed extend out in all directions forever. But of course poor Copernicus, working before the invention of the telescope, could not have known any of this.
It would take a relatively unknown astronomer in the sleepy English market town of Wallingford near Oxford to make the next big leap forward. His name was Thomas Digges and he was born in 1546, a few years after Copernicus died. His father, Leonard Digges, was also a scientist—credited with the invention of the theodolite, an instrument used (these days mainly by surveyors) to measure vertical and horizontal angles very precisely. In 1576 Thomas published a new edition of his father’s hugely popular almanac, A Prognostication Everlasting, adding new material to it in the form of several appendices. By far the most important of these was the very first English translation of Copernicus’ great work. It is fascinating to think that this was tacked on to a book on astronomy that had itself not yet taken the new Copernican theory into account. However, Thomas Digges did more than just promote and publicize this still controversial view of the Universe, important though that was. He took it further in a way that is, for me, just as important an advance in astronomy as that of Copernicus, but far less celebrated.
Digges modified Copernicus’ famous picture of the solar system, with its outer layer of stars fixed in their spherical shell around the central sun, and released those stars from their confining orbits, scattering them out into the unbounded and limitless void beyond. He was thus the first astronomer seriously to entertain the notion of an infinite universe containing an infinite number of stars (although the Greek philosopher Democritus had also hinted at such an idea).
This was no mere guess on Digges’ part. He had been persuaded of his new picture of the Universe by an event that took place in 1572. Like many astronomers around the world that year, he had been transfixed by a new bright star in the sky. Today we would identify this rare event as a supernova—an exploding star at the end of its life that, having used up all its nuclear fuel, dramatically collapses under its own weight. This process sends shock waves through the star, causing its outer layers to explode into space with one final cataclysmic release of energy. Indeed, so much energy is released in this final burst that it briefly outshines an entire galaxy. But in the sixteenth century, such astrophysical detail was not yet understood. Indeed, it was thought that as the structure of the Universe beyond the Moon was fixed and unchanging, for an object in the sky to shine brightly for a while before eventually dimming again it would have to be very close to the Earth, and certainly within the orbit of the Moon.
Digges was one of several astronomers (others included the great Tycho Brahe) who calculated that the 1572 supernova had to be very far away. Since no daily shift in its position relative to other stars, known as “parallax,” was seen, astronomers were forced to deduce that it was farther away than the Moon and planets. This was perplexing in the extreme, for it was believed at the time that beyond the Moon and planets the Universe was fixed and unchanging; and yet here was a heavenly body that had suddenly appeared from nowhere. It was referred to as a “new star,” and its appearance led Digges to conclude that the stars need not all be the same distance from us—maybe (as seems so obvious to us today) the brighter ones were nearer and the fainter ones much farther away. Such an idea was literally revolutionary at the time.
As he contemplated the idea of an infinite space with an infinite number of stars, Digges was inevitably led to ask the crucial question: why is the night sky dark? For Digges, however, there was no paradox. He just assumed that the distant stars were simply too faint to contribute any light.
What Digges was missing was a vital mathematical calculation that would have shown the error in his reasoning about the darkness of the night sky. But that was to come later. In 1610 Johannes Kepler revisited the problem, arguing the reason it was dark at night was simply because the Universe was finite in extent: the darkness between the stars was the dark outer wall enclosing the Universe. Over a century after Kepler, another astronomer, the Englishman Edmond Halley, looked at the problem again and came out in support of Digges’ original solution: that the Universe is infinite, but that the distant stars are too faint to be seen.
Figure 3.1 Three models of the Universe
It was a Swiss astronomer by the name of Jean-Philippe de Chéseaux who showed, a few years later, that this does not help resolve the problem. He proved, using some neat geometry, that if we imagine all the stars grouped into concentric shells around us, like the layers of an onion, extending out to infinity—and assuming that on average the stars are all of the same brightness2 and are distributed evenly throughout the Universe (which we know is not the case, but is nevertheless an acceptable assumption to make for the purposes of this proof)—then, while the stars in the innermost shells will shine most brightly, the shells farther out, which because they are larger in volume contain more stars, have an overall brightness that is exactly equal to any of the inner shells. In other words, lots of more distant and therefore fainter stars contribute as much light in total as fewer, nearer, and hence brighter ones. We seem to be back where we started, with Kepler’s argument that the Universe cannot be infinite or the night sky would not be dark.
Enter Heinrich Olbers, who again posed the problem of the darkness of the night sky in a paper he published in 1823. He offered a different solution. He knew, thanks to de Chéseaux, that the faintness of distant stars does not help resolve the puzzle. Instead, he argued that space is filled with interstellar dust and gas that would block the light from the more distant stars (or, as we now understand, the galaxies). What he failed to realize was that, given the length of time the Universe has been around, even this material would slowly heat up, owing to the light it absorbed, and would therefore eventually shine with the same brightness as the stars (or galaxies) it obscured.
In any case, Olbers’ posing of the problem and his proposed solution were pretty much completely ignored by other astronomers right up to the end of the nineteenth century. But perhaps Olbers can be forgiven his mistake. You see, until this point, not only did astronomers not know how far out the Universe extended, they didn’t even have good evidence that stars clustered in galaxies and that our Milky Way was just one of billions of galaxies scattered over vast distances. This would all change in the first decades of the twentieth century, when one man gave science a new view on the nature of space and time.
In 1915 Einstein published his greatest work. It wasn’t his famous equation, E = mc2; nor was it his work on light, which won him the Nobel Prize. It is called his General Theory of Relativity, and in it he describes how the force of gravity affects space and time. We learn at school a description of gravity that Isaac Newton gave us: that it is an invisible force acting to pull all objects together. Of course, this is quite right, and we live our lives under the influence of our planet’s gravity holding us to its surface. Newton’s law of gravity also explains how the Moon orbits the Earth and how its gravitational pull affects the ocean tides; and it explains how the Earth orbits the Sun, thus confirming Copernicus’ heliocentric model of the solar system. Indeed, it is the predictions of Newton’s law of gravity that were used by NASA scientists when they sent the Apollo missions to the Moon. We are in no doubt that this universal law works. But it is not completely precise.
Einstein’s General Theory of Relativity describes gravity in a radically different, and far more accurate, way. It says that gravity isn’t really a force as such—like an invisible rubber band that pulls all matter together—but rather a measure of the shape of space itself around all masses. Now, unless you have a background in physics, these words will no doubt mean little to you. Don’t worry; when Einstein first published his theory it was said that just two scientists in the world understood it. Today, it has been tested and prodded so rigorously that we are left in little doubt of its correctness.
Since our Universe is basically space with stuff in it, and all stuff is governed primarily by gravity, it quickly became clear to Einstein and others that it should be possible to use the General Theory of Relativity to describe the properties of the whole Universe. But Einstein soon encountered a serious problem. If, at a given time, all the galaxies in the Universe are stationary relative to each other, and assuming the Universe is finite in size, then their mutual gravitational attraction should cause them to begin to converge in on each other, setting in motion the eventual collapse of the Universe. The generally held view at the time was that the Universe, at the level of galaxies and larger, was static and unchanging—the idea of an evolving, dynamic, and changing universe on the very largest scales seemed to be both alien and unnecessary. So when Einstein’s General Relativity equations suggested that the Universe should be shrinking, he decided, rather than contemplating a radical rethink, to patch things up. He argued that in order to balance the inward pull of gravity there needed to be an opposing force of antigravity, known as the cosmic repulsion force, which would balance the gravitational attraction and keep all the galaxies apart and the Universe stable. What Einstein had suggested was a mathematical trick in order to reconcile his General Theory with the prevailing model of a static universe.
But then came something of a surprise. In 1922 a Russian cosmologist by the name of Aleksandr Friedmann came to a quite different conclusion. What if Einstein were wrong and there were no force of antigravity holding the Universe balanced and stable? He realized that this would not necessarily mean that it had to be collapsing in on itself under the pull of gravity. It might also mean that the Universe is doing the opposite and is expanding. How could this be? Surely, without a cosmological force of repulsion the Universe had to be shrinking, not growing. Well, here’s how.
Imagine that something had set the Universe expanding in the first place—some initial explosion. The gravitational pull of all the matter in the Universe would then be trying to slow the expansion down. So, if there were no cosmic force of repulsion to balance the attraction of gravity, and if the Universe had started off expanding (for some reason), then it would have to be either expanding or contracting at the present time. What it could not be was static: poised between expansion and collapse. That option is unstable.
Here is a simple example to demonstrate this. Consider what happens to a ball on a smooth slope: if placed halfway up the slope it will always roll down. But if we were watching a movie of the ball on a slope and paused the film with it frozen halfway up (or down) the slope and asked someone to predict what the ball would do next when we resumed play, then if they thought about it they should answer that it could be either rolling up the slope (which corresponds to an expanding universe) or rolling down the slope (a collapsing universe), but it could not be standing still. Of course, the only way it could be rolling up the slope would be if it had deliberately been given an initial kick. In that case, its motion up the slope would always be slowing, and it would eventually come to a stop and begin to roll down.
No one, not even Einstein, was prepared to believe Friedmann’s theory—not until experimental proof was found. This came just a few years later. The astronomer Edwin Hubble was the first to prove that other galaxies existed beyond the Milky Way. Until then, it was believed that the tiny smudges of light that could be seen through telescopes were clouds of dust, called nebulae, within our own galaxy. With his powerful telescope, Hubble found that these other galaxies were too far away to be part of the Milky Way and therefore had to be galaxies in their own right. Even more remarkable was his observation that the farthest away of these galaxies were flying away from us at a speed that depended on their distance from the Earth. This seemed to be happening in whichever direction he pointed his telescope. He had proved that Friedmann’s idea of an expanding Universe was correct.
Hubble argued, correctly, that since the Universe is now expanding, then in the past it must have been smaller. So if we went back far enough in time we would reach a point when all the galaxies overlapped each other and the Universe would have been pretty cramped. Go back even further in time and all the matter gets more and more squashed together until we reach the moment of the Universe’s birth, that great explosion which we now call the Big Bang (a term first coined by the astrophysicist Fred Hoyle in the 1950s).
It is worth stating here that a common misconception of the expansion of the Universe is that all the other galaxies are flying through space away from our own. This is wrong. In fact, it is the empty space in between the galaxies that is stretching. It’s also worth mentioning another interesting point—namely that our near-neighbor galaxy Andromeda is actually moving toward us! According to current estimates of the expansion rate of the Universe, it should be moving away from us at a speed of 50 kilometers per second. Instead it is moving toward us at 300 kilometers per second! The reason for this is that, just as stars are not evenly spread out through galaxies, so the galaxies themselves are not regularly distributed across the Universe. What Hubble had been observing was very distant galaxies moving away from us, rather than movement among those that make up our local cluster.
The speed at which our galaxy and Andromeda are moving together is equivalent to circumnavigating the globe in two minutes, or crossing the distance between the Earth and the Sun in under a week. In fact, Andromeda and the Milky Way are on a collision course, but at the current rate it will take several billion years for the two galaxies to merge.
One final point to make about the expansion of the Universe is that it appears that the rate at which it is expanding is increasing. It seems that, rather than gravity slowing down the expansion, something even stronger is pushing galaxies apart at an ever-increasing rate. It would appear that some mysterious force of antigravity, dubbed “dark energy” for want of a better name, is at work. And so Einstein’s idea of a force of cosmic repulsion was not so crazy after all—but now, instead of holding the Universe stable, it seems to be driving it apart.
Cosmologists now believe that while the Universe has indeed been expanding since its birth at the Big Bang almost 14 billion years ago, for the first 7 billion years the rate of expansion was slowing down, thanks to the gravitational pull of all the matter it contains—and then, during the second 7 billion years, that matter (the galaxies) became so spread out that gravity lost its grip. At this point dark energy started to take over, stretching space out faster and faster. What this means is that we now think that the Universe will never collapse back into itself again, in what is called the “Big Crunch” (as was thought possible all the way up until 1998, when the acceleration in expansion was discovered), but will instead die a “heat death” as everything moves away from everything else forever—a somewhat depressing thought, I suppose. Not that we’ll be around to worry about it, of course.
Understanding that the Universe is expanding is actually enough to enable us to solve Olbers’ Paradox—but let’s go one important step further and prove that it is expanding because there must have been a Big Bang. Apart from the irrefutable evidence coming from the expansion of space, the Big Bang theory is today also supported by two other crucial pieces of evidence. The first concerns the relative proportions of different chemical elements in the Universe—what is known as the “elemental abundances.” It is a fact that most of the atoms in existence are hydrogen and helium, the lightest two elements, with just a tiny amount of matter consisting of all the rest (oxygen, iron, nitrogen, carbon, and so on) put together. The only way to explain this satisfactorily involves a universe that was initially hot and dense, and then rapidly cooled as it expanded.
At the moment of the Big Bang, long before stars and galaxies had had a chance to form, all the matter in the Universe was squeezed together and there was no empty space. Immediately (much less than a second) after the Big Bang, subatomic particles began to form and, as the Universe expanded and cooled, these particles were able to stick together to make atoms. The conditions of temperature and pressure had to be just right for these atoms to form. If the temperature had been too high then the atoms would not have been able to remain intact and would have instead been smashed apart in the hectic maelstrom of high-speed particles and radiation. On the other hand, once the Universe had expanded a little more, the temperature and pressure had dropped too low to enable the atoms of hydrogen and helium to be squeezed together to form any other (heavier) elements. This is why mainly hydrogen and helium formed in the early Universe, a process that would have happened in the first few minutes after the Big Bang. Almost all the other elements had to wait until they could be cooked inside stars, where the conditions of ultra-high temperature and pressure were again available and where the process of thermonuclear fusion enables lighter atoms to be squeezed together to make heavier ones.
So the Big Bang theory is the only option for predicting the correct proportions of hydrogen and helium observed by astronomers today.
The other piece of evidence in support of the Big Bang was, just like the expansion of the Universe, predicted theoretically before it was confirmed experimentally. We know now that most of the light traveling around in space is not starlight at all, because the Universe is awash with ancient light that has been around since before any stars or galaxies had even formed. Less than a million years after the Big Bang took place, when the Universe was only about two-hundred-thousandths of its current age, the very first atoms began to form. At that moment space became transparent to light and radiation was free to travel vast distances. This light, the glow of that first universal dawn, has since then been stretched as the space it moves through has expanded. It was calculated that this light would have such a long wavelength by now that it would be beyond the visible spectrum. In fact, it would be in the microwave region. This is why it is called “cosmic microwave radiation.”
This radiation, permeating the whole universe, can be picked up by radio telescopes as a faint signal from deep space. This was done for the first time in the 1960S and has been repeated many times since with ever-increasing sensitivity. Incredible as it may seem, we are able to hear the hiss of these faint waves as they are picked up by our radios and television sets.
So, the fact that our Universe had a beginning is no longer in doubt. Our three pieces of evidence are: the background radiation (the afterglow of the Big Bang—at just the right wavelength); the relative proportions of different elements; and the expansion of space that we see so clearly through our telescopes. All three point to this moment of creation.
Now, at last, we can finally lay Olbers’ Paradox to rest.
Let us recap. The reason the night sky is dark is not that the Universe is finite in size; for all we know, it may go on for ever. It is not that the distant stars are too faint; the farther out we look, the more star-filled galaxies there should be, contributing their cumulative light to brightening up the gaps we can see between the stars of our own galaxy as we look out into space. Nor is it that the light from the farthest reaches of space is blocked from us by dust and gas that absorbs it; given enough time, this intervening matter will also glow as it gradually absorbs the light energy it is blocking. No, the real reason for the darkness of space is more simple and profound than any of these suggested explanations. The night sky is dark because the Universe had a beginning.
Light travels at the mind-boggling speed of over 1 billion kilometers per hour. That’s equivalent to traveling all the way around the Earth seven times in a single second. This speed is the cosmic limit for our universe. Nothing can go faster than light. It is not so much that light is special as that the speed itself is part of the fabric of our space and time. Light doesn’t weigh anything, and this is what enables it to travel at the cosmic speed limit. Einstein showed this beautifully in the first of his theories of relativity, known as Special Relativity (which we will meet again in future chapters), in 1905—and yes, if you must know, this is the theory that leads to the E=mc2 relation.
And yet, on the cosmic scale the speed of light is not so impressive. For the distances that separate us from the stars in our galaxy, never mind the distances between galaxies, are so vast that the light from even our closest neighbors takes years to reach us.
It is the very finiteness of the speed of light that helps us resolve Olbers’s Paradox. Since the Universe is nearly 14 billion years old, we can only ever see those galaxies that are close enough to us for their light to have had time to reach us. The expansion of space complicates matters, of course. A galaxy that we say is 10 billion light-years away from us is one whose light has been traveling toward us for 10 billion years. But during that time the space between us and that galaxy has been stretching, so the true current distance to that galaxy is in fact several times as great as that. However, a galaxy even twice as far away as this one is out of our range; its light is still in transit toward us and we cannot see it. So it cannot contribute any brightness to the night sky. We can see out into space only as far as the age of the Universe allows us to.
What we can see in the sky, therefore, is just a tiny fraction of the whole cosmos. We call this the “visible universe” and we cannot, even with the most powerful telescopes, see beyond this horizon in space. And this is because it is also a horizon in time. The farther out we look, the farther back in time we are looking, because what we are seeing is the light that left its origin billions of years ago; and so we see it for what it was, not what it is. The edge of the visible universe is to us therefore also the earliest moment in time. And here is that final subtlety regarding the expansion of space. Even if an infinite static (not expanding) universe had suddenly popped into existence 14 billion years ago, we still would not be able to see beyond 14 billion light-years. So it is not the expansion itself that stops us seeing to infinity. For if we could wait long enough in a static universe then the light from ever-farther galaxies would eventually reach us. It is just that beyond the edge of our visible universe the light will never outrun the expansion, like walking too slowly down an escalator that is going up.
In the previous chapter I made the point that in order to resolve Zeno’s paradoxes we needed to appeal to rigorous science rather than abstract logic alone. But when it comes to Olbers’s Paradox the first correct resolution was one based on intuitive logic rather than good science, and it came from the most unexpected of quarters: the nineteenth-century American author and poet Edgar Allan Poe.
The year before he died at the age of forty, Poe published what is widely regarded as his most important and influential work, an essay called Eureka: A Prose Poem (1848). Adapted from a lecture he gave and subtitled “An Essay on the Material and Spiritual Universe,” it is a remarkable piece of literature. It has no credibility as an actual work of science, being more to do with Poe’s intuition about the laws of nature. In a sense, it is a treatise on cosmology in which Poe speculates on the origin of the Universe, its evolution and its end—and in which he relies on a mixture of logic and wild speculation rather than on valid scientifically backed ideas. For instance, he develops his own notions about how Newton’s laws apply to the way planets are formed and how they spin, which are quite wrong. Nevertheless, buried in the essay is the following famous passage:
Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy—since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids, which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all.
So there you have it. Olbers’s Paradox was first resolved correctly not by a scientist but by a poet. Some historians argue that Poe’s description is just guesswork and that it wasn’t until a proper calculation was carried out by one of the nineteenth century’s greatest scientists, Lord Kelvin, and actually published in 1901, that we can truly say the paradox was resolved. But Kelvin essentially provides the mathematical proof of Poe’s idea. Whether we like it or not, Poe was right on the button.
So, the answer to our initial question Why does it get dark at night? is simply that the Universe started with a Big Bang.
Scientists are often asked what proof they have that the Big Bang actually happened. They usually quote the three standard pieces of evidence I discussed earlier. But isn’t it so much easier, and in my view more persuasive, to turn Olbers’ Paradox on its head? Rather than saying that the reason it gets dark at night is that the Universe must have had a beginning and that there has therefore not been enough time for light beyond a certain distance to reach us, why not try out the argument the other way around? For if anyone wants proof of the Big Bang they need only venture outside at night and ponder the darkness of space.
The real puzzle is that it took astronomers so long to figure this out.
2 Of course, at a certain distance we will have extended out beyond the Milky Way and, rather than talking about stars, we would have to think about galaxies.