Chapter 6
Beyond Democratic Capitalism
An Idealized Political Economy, with Distributive Justice
Throughout this book, I have been quite critical of Western political economies, the United States in particular. But in the latter case, I have tried to be constructively critical, proposing concrete solutions to practical problems. In this final chapter, I want to go deeper and address several philosophical questions that matter because our views on these issues impact how we think and thus how we act: What might an ideal political economy consist of? How does today’s form of democratic capitalism compare with such an ideal? Does it deserve its tarnished reputation? At a more fundamental level, what properties do people truly value and seek from their economic and political systems? Is the capitalist norm of economic “efficiency” enough, as an economics textbook might well suggest? Or are there other norms? In particular, is there room for justice and fair sharing of the pie along with economic efficiency? Finally, what about privacy and freedom? Can these be accommodated as well? As will be seen, the answer to this last question is yes. All these norms can be accommodated side by side. Thus, just as the five previous chapters do, this final chapter conveys a strong message of optimism.
While it is currently unfashionable to pose “big” questions such as the nature of an ideal social system, the need to do so has arguably never been greater. There is a sense that democratic capitalism is now failing to deliver the goods, at least in Europe and the United States. Living standards are falling for the middle and lower classes. Unemployment is high and failing to come down. Perceived maldistributions of wealth are causing protests and riots throughout the West, and this is just the beginning of what will happen as overstretched welfare-state governments start to renege on their promises to an aging population of unaffordable pension and medical benefits.
Do you know anyone who is not concerned about the future, regardless of his or her political leanings? There is widespread recognition that today’s elected politicians are unable to arrive at compromises that will solve our problems. Polls in many nations rate politicians at the bottom of popularity lists. Few people believe that Right-wing or Left-wing candidates have meaningful answers to today’s most important questions.
In the West, questions are beginning to be raised about the long-term viability of democracy itself. If today’s dysfunctional system leads to further financial crises, to soaring debt and credit downgrades, and to falling living standards, how long will it be before we elect that “strong man” who promises to make the trains run on time once again? And once he is in power, how long will it be before a one-party state emerges and civil liberties are curtailed? Such a question was unthinkable in the West during the decades since the defeat of fascism during World War II, and since the implosion of communism in 1989 that was celebrated by Francis Fukuyama’s book The End of History and the Last Man. After all, we liberal democratic capitalists were the victors, at least so we were told. But was ours a Pyrrhic victory?
I shall start off explaining why true capitalism properly understood represents one of the great institutional innovations and successes of history. As the eminent New York Times journalist David Leonhardt wrote in his economics column published on July 27, 2011:
Economic truths may not rise to the level of certainty of two plus two equals four, but they are not so different from the knowledge that the earth is round, or that smoking causes cancer. When it comes to economics, we know that a market economy with a significant government role is the only proven model of success. The United States has outgrown Europe because of our greater comfort with market forces. . . . On the other hand, unencumbered market forces often lead to disaster, as 1929 and 2008 made clear.
But what exactly is Leonhardt claiming here? What are the various economic, institutional and governmental preconditions for successful capitalism? What are the precise circumstances under which Adam Smith’s concept of the “invisible hand” really does work as advertised, and under which it fails? As we review these, we will see that true capitalism does not represent some libertarian alternative to a system with a strong government. For strong and good government has been presupposed by capitalist theory from the time of Adam Smith, a point many self-styled conservatives seem to have forgotten.
This section culminates with a definition of the public good as given in classical economics. This makes clear what the market and the government should each do to maximize the public good, or in economics jargon, to achieve an efficient allocation of private and public resources. This ideal provides a yardstick to demonstrate the extent to which real-world “bastardized capitalism” falls so short of the mark. In this regard, I introduce a unified explanation of why real-world capitalism often lets us down.
The second section of the chapter builds on the classical results of the first, but delves much deeper. It investigates the concept of idealized social systems. More specifically, we investigate those properties above and beyond economic efficiency that might characterize an ideal economic resource allocation system. For example, do not most of us value the properties of freedom, justice, and equality, informational efficiency, stability, and privacy, along with classical efficiency? Drawing upon the brilliant work of the late Nobel laureate Leonid Hurwicz, I explain how “snow-white capitalism” alone is consistent with all these norms. By this term, I mean the perfectly competitive free market backed up by the rule of law.
The chapter then shifts to the polarizing issue of justice, and in particular the subject of distributive justice, which concerns the optimal distribution of wealth and income. My principal goal is to show how issues of redistribution are not “outside” of free market economics, but in fact integral to it. In particular, I demonstrate how a belief in the principles of true capitalism logically requires a belief in redistribution. This is a theorem based on the role of luck in life, not a speculation, and it is one that will make many anti-redistributionists do a double-take!
Fortunately, great progress has been made in the past few decades in clarifying the topic of fair distribution, and it has been a focal point of my own research for several decades. I want to bring readers up to date and argue once again that the issues here are neither Left wing nor Right wing in nature, but much more fundamental. Anyone doubting the relevance of the topic of distributive justice should remember that Harvard’s Michael Sandel has become the rock star of international academics largely because of his focus on this issue.1
Students worldwide recognize justice to be the most fundamental of all topics. They like being made to think about it, and to argue about it. The rest of us largely sidestep the issue, Republicans and Democrats alike. Holding a belief about “repealing the Bush tax cuts” does not amount to possessing a theory of justice. For starters, no one has even tried to demonstrate that tax rates either before or after the Bush cuts were fair in any sense. Heaven help us if our stance on this issue is supposed to proxy our political philosophies!
The chapter concludes with a sketch of what an ideal political economy might resemble, one that far transcends classical concepts of the public good by explicitly integrating within it the two fundamental strands of distributive justice: to each according to relative need, and to each according to relative contribution.
True Textbook Capitalism, and the Correct Role of Government
When Bill Clinton went to Oxford as a Rhodes Scholar, he studied the traditional Moral Tripos known at Oxford as PPE (Philosophy, Politics, and Economics). There, he and his fellow Rhodes Scholars presumably learned that Adam Smith’s original analysis of market capitalism was in fact an investigation into moral theory in a broad sense. Indeed, the ideas underlying Smith’s Wealth of Nations of 1776 were rooted in his predecessor treatise A Theory of Moral Sentiments of 1759. Accordingly, as economic theory developed during the next two centuries, emphasis was often put upon such morally pregnant concepts as nonwastefulness (now known as “efficiency”), and distributional equity.
In short, the links between capitalist economics and moral philosophy were deep and abiding from the start. It is easy to overlook this tradition when, in today’s ideological environment, a belief in capitalism has degenerated into a belief that “markets know best,” that the principal virtue of free markets is that they result in maximal efficiency, and that the role of government should be as limited as possible. To be sure, many people who have studied and understood Econ 101 know that the government must redistribute income since it cannot avoid doing so—as when it raises revenues to fund public goods, just as it must intervene to remedy “market failures” such as pollution and the excess leverage we have discussed earlier.
Nonetheless, this is acknowledged in an increasingly grudging manner—as an agenda that can be ignored as we celebrate the role of decentralized free markets in generating an efficient allocation of resources. This bias distorts the truth about genuine capitalism, namely that it is a social system in which government and businesses and consumers work hand in hand to maximize the public good, always subject to such constraints on unfettered free enterprise as are required to reach this maximum.
What exactly are the prerequisites for a capitalist economic system that seeks to maximize the public good? There are three kinds:
1. The Rule of Law: For free markets to function correctly, the rule of law must prevail. Citizens must benefit from the sanctity of contracts, nonbribable judges, transparency in commercial relations, and the protection of intellectual property rights. Without such protections, capitalism morphs into crony capitalism in which deference to the concept of “free markets” is hot air at best.
2. The Economic Preconditions for Decentralized Free Market Transactions to Maximize the Public Good: As students learn in their textbooks, the following five requirements must be met for the full promise of the invisible hand to be fulfilled.
i. Perfect competition—in particular the absence of any bargaining power by any group whatsoever whether cartels, labor unions, or oligopolies. This first assumption requires that product and labor markets must be fully deregulated and highly competitive. Every individual producer and consumer takes prices as given by the invisible hand and has no ability to set prices, or otherwise rig markets.
ii. Diminishing marginal utility for all goods and services, the property whereby your fourth Coke during a hot afternoon satisfies you less than your third Coke, which satisfies less than your second Coke, and so on.
iii. The existence of complete markets for hedging, that is, insurance markets permitting all risk averse agents to hedge every and any risk by creating appropriate portfolios of derivative securities.
iv. The absence of nonmarket phenomena or “externalities” such as pollution, where the price system either fails to operate, or else misallocates resources.
v. Diminishing returns to scale on the part of most (but not all) industries.
If all of these conditions are met, then it can be proved that a decentralized free market system will generate the largest “pie” possible out of the resources available. That is, the outcome will be efficient and nonwasteful. This is the principal result of Microeconomics 101, first proven formally by Kenneth Arrow in his 1953 paper that extended invisible hand economics to include uncertainty about the future, and in doing so identified requirement number (iii) on hedging. Note that the role of government and “politics” is absent from this simple model, except for the presupposition that the rule of law is in place. I shall refer to such idealized microeconomies as snow-white economies.
Next we add the prerequisites required to provide public goods, and to deal with externalities and with the lack of perfect competition.
3. Governmental Preconditions to Cope with Externalities, Imperfect Competition, and the Provision of Public Goods
The following four requirements must be addressed:
i. Need to regulate business cycles and financial market crises via appropriate fiscal and monetary policies.
ii. Need to redress market failures or “externalities” (e.g., pollution) and to provide basic public goods (e.g., a legal system, a military system, etc.).
iii. Need to enforce perfect competition and to prevent the formation of cartels to the extent possible.
iv. Need to address any issues of distributive justice that arise within the economic system and cannot be wished away.
As for distributive justice, once the need for public goods arises (e.g., an army must exist, sewers must be built), a decision must be made by government as to who should be taxed how much to pay for it. This is a political decision made by a very “visible hand,” not a market decision made by an invisible hand. Thus issues of taxation that are fair inexorably arise within capitalist theory.
Classical Definition of the Public Good
To recap, a world of true capitalism is one in which all three of the previous sets of conditions are satisfied.2 The result will be an efficient allocation of resources, and one which is fair assuming that government explicitly addresses the issue of fair distribution. We shall define such an outcome as one that maximizes the public good in a classical sense.
This concept of the public good provides a yardstick against which any nation can ascertain how far it is from the ideal, and can determine how to improve upon the status quo given the political will to do so. Be sure to note how far this ideal lies from today’s presumption that capitalism is all about the unfettered play of free markets. It is not, and never was, even though the healthy functioning of markets is indeed central to its success.
The Bastardization of Capitalism
The arguments I have made earlier in this book should make it clear that today’s U.S. political economy lies far away from this ideal. This is evidenced by sluggish growth, an inequitable distribution of wealth and income, a preposterous system of health care, an over-leveraged financial system, an excess of consumption over investment—especially nonexistent public sector investment, unchecked cartels making a mockery of perfect competition, lobbyists buying access in Washington, and a system of entitlements skewed towards the interests of today’s elderly at the expense of future cohorts of the elderly.
At a much more abstract level, what goes wrong is the politicization of economics. As I discussed in Chapter 5, Robert Aumann’s 1977 theorem showed that, in a truly capitalistic world of perfect competition and the invisible hand, no agents possess any bargaining power at all. To restate his result, the allocation of goods and services resulting from free-market behavior is untainted by any form of bargaining power (i.e., of politics). In such a world, there will be no K Street lobbyists, no self-dealing, no cartels, no rock-bottom “carried interest” tax rates for millionaires and billionaires in finance, no regulatory decisions not in the public interest, and so forth.
Well, the real world is a far cry from Aumann’s idealized world of “strategically inert” market participants. It is one where lots of bargaining power exists so that the final allocation of resources is the result of multilateral bargaining behavior. Powerful interest groups attempting to achieve their goals utilize credible threat strategies. Their most common threat strategies are threats not to make campaign contributions unless regulatory decisions go their way. As a result, “might makes right” all too often. This is the genesis of the corruption and distortion in the resource allocation that is causing increased consternation by the public at large, and by the Occupiers of Wall Street most notably at this writing.
In some idealized fantasy world of snow-white politics, the machinations of all these interest groups would be replaced by the deliberations of some philosopher king who would arbitrate every regulatory decision on the basis of “maximizing the greatest good for the greatest number,” or some related politically neutral norm. What a far cry this would be from today’s world of K Street lobbyists!
How bad is today’s bastardized form of capitalism? Should we get discouraged and seek an alternative form of a resource allocation system? No, we should not, for as we are about to see, capitalism on balance works very well and is much too precious to throw out, warts and all. To understand this, it is necessary to understand the seminal work of Leonid Hurwicz.
Beyond Efficiency: The Eight Ideals of an Optimal Social System
One wintry morning in Cambridge, Massachusetts in the early 1970s, when I was an applied mathematics graduate student, I visited the economist Kenneth Arrow in his office at Harvard, seeking some advice from on high. He mentioned that I should not miss taking a course from an old friend of his who was visiting Harvard at that time and was known within the economic theory community as a brilliant original thinker, Professor Leonid Hurwicz. I knew little about Hurwicz, but took Arrow’s advice and took the course. It was the single best course I have ever had. To begin with, Hurwicz was a superb and patient teacher who explained very complex things very simply.
But most important, Hurwicz was a very big thinker. He generalized economic science in a breathtaking manner. Traditionally, most economists had simply investigated how to tweak an economy so that it could deliver an efficient allocation of resources, which was until then the Holy Grail of economics. Hurwicz, by contrast, focused not on a given economy, but rather on the set of all possible economies or resource allocation systems (e.g., capitalism, communism, socialism, whatever). And he asked not merely which system was most efficient, but how each system ranked according to numerous other norms that will be discussed shortly. His colleagues came to call his enterprise the theory of “mechanism design.” Hurwicz mathematized it, and thus transformed previous thinking about alternative social systems into a proper branch of science. For this contribution, he would earn the Nobel Memorial Prize in Economic Sciences in 2007.
I will start off by setting forth the norms an ideal political economy should satisfy, and then cite his main analytical result about the status of capitalism. Think of each of the following eight norms as a property that almost everyone would like to be satisfied by their social system.3
Eight Idealized Properties of an Optimal Political Economy
An initial caveat is in order. Hurwicz originally restricted himself to the case of what I have dubbed “snow-white” economies, that is, resource allocation systems satisfying the first two groups of prerequisites identified previously. Accordingly, while the rule of law is assumed, there are no issues of externalities or public goods to be arbitrated by government. While more recent work permits these to be included, the exposition will be clearer if we stick to his simplest and earliest results. Here are the properties we might all hope for in a resource allocation system:
1. Classical Efficiency: A resource allocation system is classically efficient if the outcome is the largest pie possible given the endowments (skills and wealth) of the citizens, and given the state of technology of the day. Another way of defining efficiency is to require that, if any one agent is to be made better off by virtue of some reallocation of goods and services that were produced, then at least one other person must be made worse off. There is no “waste” in this sense. There is no slack in the system. As a norm, efficiency is like apple pie or motherhood: Who could be opposed to it? Who wants waste?
2. Dynamic Stability: The stability of an allocation system refers to the degree to which the system is stable once it is subjected to shocks. The shock could be a market crash, a hurricane, or whatever. If the system is stable, then after a finite period of time, things will return to the way they were. Most people equate stability with a sense of security, and value this property.
3. Optimal Growth of Wealth and Income: Independent of Hurwicz’s work, research by T. Koopmans and E. Malinvaud in the 1950s permitted pure capitalist theory to be rendered dynamic rather than merely static. As a result, the concept of economic growth over time could be studied and, more important, the concept of optimal growth could be defined. Other things being equal, people prefer a system in which wealth and living standards rise rather than fall, and do so in an optimal manner. Who doesn’t want a better tomorrow? I am taking liberties in adding this norm to those Hurwicz himself proposed, because he easily could have added it, and because this norm matters to people.
4. Informational Efficiency: This particular norm emerged from a debate that raged during the mid-twentieth century between free-market theorists and central planners. As early as the 1920s, socialists and communists believed that an efficient allocation of resources could be achieved by central planning. Planners could, in principle, determine who should produce how much, and who should consume how much of every commodity produced. No invisible hand price system was required.4 What Hurwicz and others show is that decentralized invisible hand pricing without the bureaucracy of central planning is much more “informationally efficient” than central planning could ever be. That is, far fewer data about individual people’s endowments, preferences, and firms’ modes of production are needed in a market-based system than in a centralized system to arrive at an efficient outcome. Hurwicz deemed this kind of efficiency desirable, especially because of its close relationship to the next two norms.
5. Decisional Decentralization or Freedom: This norm represents the degree to which an agent can make decisions on his own in order for the system to function efficiently. Does someone else (e.g., the state) need to tell him what to do? Does he require permission slips from Big Brother before making a decision as to what to order for dinner? This is a very reasonable norm since most people prefer the freedom associated with decisional privacy to a lack of such freedom.
6. Informational Decentralization or Privacy: This norm refers to how much information different agents need to know about each other’s preferences or production processes in order for the resource allocation system to function. When I decide to manufacture my firm’s metal vessels using my own technology and resources, need I know how other manufacturers are making their vessels, and how many vessels each is making? It certainly facilitates my life if I have no need to obtain data about others. Analogously, when I decide what to serve my guests for dinner, need I know what all other hosts are serving their guests? Most people like privacy, and the less we need to know about other people’s business, the better.
7. Equity, Including Distributive Justice: Most people prefer systems and outcomes that are fair, or equitable. The reason they do is that each of us has experienced being treated unfairly, and we do not like it. The problem, of course, is to know what the term “fair” means. In some contexts, this is easy: We all want to be tried by a jury that is unprejudiced so that the deck cannot be stacked against us. The more difficult context is that of distributive justice: What distribution of the pie is fair? The seemingly zero-sum nature of this deepest of all questions makes the answer all the more difficult to arrive at. The final two sections of this chapter will focus on precisely this issue.
8. Incentive Structure Compatibility: This norm was the crown jewel of Hurwicz’s work. Now the concept of incentive compatibility is somewhat abstract and thus deserves an explanation of why it qualifies as a desirable norm. Briefly, let us identify alternative resource allocation systems (capitalism, communism) by the rules of the game that define each. These rules consist of all the penalties, rewards, and regulations that incentivize people to make the decisions they do. I use the term incentive “structure” in order to stress that, for any resource allocation system, the rules of the game consist of all incentives impacting the decisions of all agents.
For a long time, everyone has known what Steven D. Levitt and Stephen Dubner stressed in their delightful book Freakonomics, namely that incentives strongly impact individual behavior. Just think of the impact on smoking of cigarette taxes and other penalties. Or recall the old saying “Spare the rod, spoil the child.” What Hurwicz did is to investigate the impact of the incentive structure in its entirety on system-wide properties like efficiency, freedom, stability, fairness, and so forth. His work made it possible to “grade” alternative sets of rules of the game on the basis of how favorably they impacted the performance of the social system as a whole. To understand the power of this contribution, suppose we ask whether or not private property ownership is good for society. Hurwicz taught us to answer this question as follows. Consider the differing impact on system-wide efficiency of two different sets of rules of the game, one set permitting private property ownership, the other preventing it. All other rules are held constant so as to focus on the impact of property ownership alone. Now which of the two systems is more efficient as measured by the size of the pie that gets baked?
If the answer is that private property ownership incentivizes people in the society to act in ways that end up producing the biggest pie possible, we can then state the institution of private property ownership is incentive compatible with the goal of economic efficiency. And so forth for any or all of the six other norms we value above and beyond efficiency. The important point here is that there must be clearly specified goals (e.g., efficiency and stability) with respect to which a given social system is or is not incentive compatible in order for the term “incentive compatibility” to be well defined. This point is both subtle and brilliant!
The Principal Result
Hurwicz’s main result was to prove mathematically that the rules of the game in a snow-white market economy as defined earlier are incentive compatible with all of the norms we have identified, excluding norm 7 (equity), which requires a consensus as to what is fair, and government intervention to achieve it. In other words, individuals acting selfishly in a snow-white economy will unknowingly act in such a way as to fulfill all these ideals except for norm 7. The first intuition that this might be true (for the case of the efficiency norm) was Adam Smith’s conjecture that decentralized free-market behavior by selfish individuals would achieve the greatest possible efficiency when such behavior was coordinated by the invisible hand of the price system.
Kenneth Arrow, Gerard Debreu, and others would demonstrate the precise conditions under which Smith’s conjecture about efficiency would hold true. Hurwicz’s contribution was to extend these classical results to encompass all the above norms, not merely norm 1 (classical efficiency). Perhaps more important, he demonstrated mathematically why almost no conceivable resource allocation system other than free-market exchange will satisfy many of these norms. It is in this sense that we can now fully understand why free-market capitalism is far superior to any other system yet proposed. Moreover, Hurwicz demonstrated all this in a scientific manner devoid of ideological prejudice and thus defused what had previously been an extremely ideological debate between the Left and the Right.5
In concluding this review of Hurwicz’s contribution, I want to stress that the concept of incentive structure compatibility (norm 8) is one of the most powerful concepts ever introduced into social science. It provides the missing link between the motivations and actions of individuals on the one hand, and the performance of the entire society on the other. It made it possible to measure the true performance of alternative social systems and to do so merely by contrasting the rules of the game operative in each. An endnote explains this remarkable contribution in greater depth for the interested reader.6
Relevance of Snow White Capitalism to Bastardized Capitalism
Given that we live in a world of bastardized capitalism, as David Leonhardt of the New York Times suggested, why have I discussed Leonid Hurwicz’s results concerning an idealized world of snow-white economies? Of what possible relevance are these findings to the realities of our own flawed social system? The answer is that they could not be more relevant. The reason lies in the fact that, problematic as real-world capitalist economies might be, they contain within them subeconomies that very closely approximate the ideal described by Hurwicz. To understand how this is true, think of our economy as partitioned into two quite distinct sets of industries that coexist within one system: those riddled with cartelization and cronyism, and those that are very competitive.
Fortunately, the latter set is far larger than the former. Indeed, near-perfect competition and an absence of bargaining power typify most small businesses, most consumer electronics, agriculture, retailing, restaurants, hotels, the global auto industry, consumer products, and so forth. Competition is fierce—which is exactly why average risk-adjusted returns are modest, and why it is hard to get rich. A firm like Goldman Sachs is not representative of business at large. By far the majority of businesses do not have the bargaining power and cannot earn the returns that Goldman Sachs does. We the consumers end up the principal beneficiaries of high levels of competition.
Now ask yourself how well such highly competitive sectors perform. Each and every year, most of us enjoy better bedding, better and safer cars, a greater variety of foods, better consumer electronic products, a wider choice of restaurants, better hearing aids, better prosthetic limbs, better access to the movies and music of our choice, better cruise-ship destinations, and so on. The list is nearly endless. Even better, the after-inflation price of such goods tends to drop. The point is that a large part of the economy pretty well replicates the kind of snow-white competitive economy whose virtues Hurwicz captured so brilliantly.
Now contrast the performance of these competitive sectors with that of highly cartelized, noncompetitive sectors that deliver public education with negative productivity growth, decrepit mass transport systems, and “financial innovations” created by bulge bracket financial firms that have made bankers very rich while causing widespread distress on Main Street. In a different direction, note how impressively the rate of innovation in the telephone sector accelerated once the AT&T monopoly was broken up. The result was much better service for a fraction of the cost per calling minute.
The Moral of All This
So remarkable are the fruits of snow-white capitalism, or the real-world approximation to it we enjoy in many economic sectors, that we should do our best to preserve it and to build upon it. Government should strive to render uncompetitive sectors competitive, and should prevent competitive sectors from becoming uncompetitive. More generally, we must never throw capitalism out with the bathwater just because of our distress over malfeasance on Wall Street. It is tempting to do so, and people have every reason to be outraged about today’s crony capitalism that violates the predicates of true capitalism. But we must not strike back in the wrong manner lest we end up hurting ourselves.
The conviction of the have-nots that they are unfairly taken advantage of by the haves has often been cited as a primary determinant of social and political upheavals throughout the ages. The names of Spartacus, Robespierre, Marx, and Mao come to mind when we recall cries for redistribution across history. This redistributive impulse is far from dead. The outcome of the next U.S. presidential election will surely reflect widespread outrage over today’s inequalities in wealth and income.
The purpose of this section is to demonstrate how various forms of distributional equity are part and parcel of economic theory, and of capitalist theory in particular. This claim will surprise many people who have always believed that free-market economics focuses solely on matters of efficiency, not equitable distribution. But this is not true. I now show that there are five ways in which issues of distributive justice are lodged within free-market theory. I do not address the problem of what the correct distribution of wealth and income is, and how this might be determined. This larger issue is addressed via a comprehensive theory of justice sketched in the concluding section.
In reviewing how the issue of fair distribution arises within free-market economic theory, it is important to separate at the outset the two different and competing ethical norms that arise in discussions of distributive justice. On the one hand there is the contribution principle according to which each agent should receive a wage that is equal to his relative contribution to the organization paying him or her. On the other hand, there is the needs principle, according to which resources should be allocated to people in proportion to their relative needs. Further on in this chapter, I will discuss the thorny relation between these two concepts, and the question of whether both can be satisfied at once within an idealized polity.
Interestingly, both principles of distributive justice arise within classical market theory, as we will now see.
The Contribution Principle
In an idealized competitive economy, each worker will be paid a wage equal to what he contributed to the enterprise he works for. His wage will equal his “marginal product,” or contribution to his firm, as has been known for many decades. The proof of this is simple: A company that pays its workers a wage exceeding their contribution will be driven out of business because it will make losses, under perfect competition. A firm that pays workers less than their contribution will be unable to retain employees. Every manager of a business knows that importance of respecting the contribution principle. If an employee is underpaid relative to his contribution, say to corporate sales, he will know it all too well. If an employee is overpaid, everyone else will know it, and the issue of compensation will rankle and cause morale problems.
Suppose we are interested in the applicability of the contribution principle in a much broader class of environments than that of economic markets, for example, political or non-governmental organization (NGO) environments where “correct market wage rates” cannot be defined, so that the contribution principle applicable in a market context cannot be invoked. Is there a way in which contribution fairness can be respected? Remarkably, there is. Suppose that in these nonmarket environments, resources get allocated via multilateral bargaining of the kind described in the previous chapter, as they usually do. Then as John Harsanyi first demonstrated, the payoffs from multilateral bargaining satisfy a more powerful and abstract form of the Contribution Principle than the more familiar “wage = marginal product” version known from microeconomics.7
The Trade-Off Between Efficiency and Equity
Many people believe that the two norms of equity and efficiency are intrinsically at loggerheads because of “incentive effects.” If the tax code is too progressive, then the wealthy and productive will reduce their contribution of labor and capital such that the pie will grow less rapidly, or possibly shrink. While there is some evidence to support this view, it is highly controversial except in extreme cases where wealthy and productive people are excessively penalized. But for game theoretical reasons demonstrated in an important paper by Professors Robert Aumann and Mordecai Kurz, punitatively high tax rates rarely should be and rarely are imposed in the real world.8
But there is a different and much deeper way in which equity and efficiency concerns are commingled in capitalist economics. The dominant virtue of an invisible-hand economy is that, given the initial endowments (wealth and skills) of each agent, the outcome of market exchange will be an efficient allocation of goods and services. Now suppose government wishes to make the resulting distribution of income and wealth more equitable. For example, it could institute a lump-sum transfer from some agents to others. Can it do so without destroying the efficiency of the allocation that results? To state this differently, will there exist an efficient allocation regardless of any forced transfers made between agents?
The answer to both questions is yes, and this is known as the Second Fundamental Theorem of Welfare Economics, first proved by Kenneth Arrow and Gerard Debreu in the very early 1950s. What this established from first principles is that market-based capitalism with its virtue of efficiency is fully compatible with fairness-based redistribution. This was an extremely important result for the moral philosophical basis of capitalist theory, for we learned that equity and efficiency need not be at loggerheads at all.
Bad-Luck-Based Redistribution Due to Missing Markets
To me, by far the most important and indeed improbable link between equity and market capitalism was discovered in 1953. This was the year that Kenneth Arrow extended classical invisible hand economics to incorporate uncertainty about the future. Until then, no one had figured out how to make sense of concepts like supply, demand, price, equilibrium, and efficiency in a world where agents did not know the location of their future supply and demand curves, and thus could not forecast future prices.9
Remarkably, Arrow proved that all the main concepts and results of classical economics (e.g., market efficiency) still hold true when agents are uncertain about future supply, demand, and price variables provided one fundamental modification is made to the classical model. Once uncertainty enters the picture, an entirely new set of hedging markets would have to exist, “Arrow Securities” as they were originally known. These securities permit every agent to lay off every kind of risk about the future, and to do so in proportion to his or her risk aversion level. He could hedge against rain or shine at any future date, against war or peace, or against the success or failure of a new production process. Every unknown future “state of the world” could be hedged.
Given a complete set of such risk-spreading securities, risk-averse economic agents were not only permitted to spread their risks, but would wish to do so since it was in their self-interest. Assuming that these conditions were fulfilled, Arrow showed that—even with uncertainty present—the market will generate not only an efficient allocation of goods and services, but also an efficient reallocation of risk itself. Thus was born what many now refer to as the economics of uncertainty.
While Arrow did not comment on the revolutionary implications of his theorems for the seemingly unrelated issue of a fair distribution of wealth and income, others did. Here is the relevant logic. To begin with, the complete set of hedging or insurance markets required by Arrow’s result do not and probably never will exist. This is the “missing markets” problem investigated by Robert Shiller at Yale, and many others, and this is what matters for the distribution of wealth and income.10 This is because any insurance contract can be viewed as a redistribution of resources from someone lucky (his house did not burn down) to someone unlucky (your house did burn down). Therefore, as a result of the widespread lack of insurance transfers from the lucky to the unlucky due to missing markets, the ex post distribution of wealth and income in the real world ends up far more unequal and skewed towards the lucky (rich?) than it would be under a regime of true capitalism possessing complete markets.
One way of remedying this deficiency of missing markets would be to introduce a progressive tax code to approximate the net transfer payments that ideally would be made via complete insurance markets, but cannot be made in reality. Viewed in this manner, the progressive tax code would be not an ethical construct, but rather a remedy for a market failure, just as pollution taxes are, in a different vein. A progressive code would help restore the distribution of income and wealth to what it would have been in a world of complete markets.11
Of course there is a presumption here that wealthier people tend to have been luckier than others, and I believe this to be true to an order of approximation. Virtually any “successful” person I have known, or whose biography I have read, admits to having benefitted from lucky breaks on the road to success. As most of these breaks were events that could not be hedged, the outcome is a much greater degree of inequality than would have resulted with perfect self-interested hedging of all events. In the extreme, a winner-take-all-world emerges. The late Australian billionaire Kerry Packer put this to me better than any theorist ever has: “Woody, if you meet someone very successful who thinks he deserved his success, you know you have met a real jerk.”12 Bingo! Along the same lines, is hardly surprising how often we hear, “I would rather be lucky than smart.”
The Oprah Winfrey Book Club Lottery
The logic of luck-based redistribution is so compelling that I want to give a concrete example that really brings it home. Suppose you and I are both accomplished writers of exactly the same age and reputation. We have both sold about the same number of books, yet we both only make $75,000 per year because we write “serious” books. Now suppose a random event occurs: Oprah Winfrey opens up her book club. We both now face an equal chance that she might notice one of our next two books when they are published, read the book, and recommend it strongly to her audience. If I am the lucky one, then my income will soar from $75,000 to $5,000,000, and likewise for you if you are the lucky one.
What might we do to improve our welfare confronting this new possibility? Suppose that we are both risk averse, indeed equally risk averse. Then the Nash bargaining solution to the implied game between us will be to draw up an insurance contract whereby we split the extra $5,000,000 payoff equally should one of us luck out. Understand that this contract is motivated solely by our mutual self-interest, and not because of our beliefs about “fairness.”
Given such a contract, our two incomes will remain equal should either or both of our books get endorsed by Oprah. No “winner takes all” inequality arises. But if we do not contract away the risk involved because we cannot draw up this mutually advantageous contract, one of us will walk away with a bonanza leaving nothing for the other. In this context, a progressive income tax would then help rectify the lopsided distribution of winnings resulting from a lack of insurance—insurance required if economic efficiency is to result. The tax would have the effect of “restoring” the distribution of income that true capitalism would have generated.
The moral here will be highly disconcerting for many self-styled conservatives and other devotees of capitalism who are doubtless unaware of Arrow’s 1953 result. If you really believe in the free market, and worship at the high altar of market efficiency, then you had better rethink your position on distributive justice, and on the progressivity of the tax schedule in particular. What you have hopefully now learned is that capitalism not only implies an efficient allocation of goods and services, but also an efficient allocation of risk as well. I find it remarkable that this argument has never been exploited by self-styled liberals concerned about inequality.
One important point here is that there is nothing Left wing or Right wing about the logic I have set forth. Redistribution occurs because of acts between consenting adults wishing to pool and hedge their risks. As a result, today’s shouting match between those on both sides of the redistribution debate should be much less shrill than it is. I now turn to still other ways in which issues of redistribution are intertwined with the theory of democratic capitalism.
Fair Tax Rates for the Provision of Public Goods
The need for and provision of public goods (e.g., the army and the law courts) lies outside of the scope of the market and its invisible hand. Government must provide these, and as a result must tax people to pay for them. But at what rate should it do so? Who pays how much of the freight? This is a straightforward problem of distributive justice. There are two basic ways in which it can be and is resolved. First, the answer could be dictated by politics alone, devoid of any ethical considerations. We are back to the Nash-Harsanyi theory of bargaining of Chapter 5. Interest groups flex their muscles, utilize their relative threat power, form coalitions, and reach a compromise as to who pays how much in taxes.
The second way to allocate the tax burden is more ethical and less economic in nature, and takes into account the relative ability of agents of different types to pay for public goods. It has long been accepted, at least within modern democracies, that the poor have a much more difficult time than the rich in paying their taxes if the same tax rate on total income, say 25 percent, applies to both. Accordingly, it is fairer for the poor to be taxed at, say, 15 percent and the wealthy at 30 percent of their differing incomes in financing government spending. This is one reason why, in reality, almost every nation has a progressive tax code. British utilitarians such as Jeremy Bentham and John Stuart Mill were the first to provide a formal logic as to why the poor should pay proportionately less than the rich for government services. Why did they claim it was harder for the poor to pay the same percentage on total income as for the rich to do so? What was their logic that implied a progressive tax code?
Their explanation lay in the principle of “diminishing marginal utility.” This is the property whereby most people derive less utility (satisfaction) from the fourth ice cream cone they enjoy on a hot August afternoon than from the third cone, and less from the third than from the second, and so forth. Assuming that the government seeks to maximize the greatest good of the people when setting tax rates, the utilitarians proved that the principle of diminishing marginal utility implies a progressive tax code under which the poor pay a lower share. The philosophy that government should always select policies—including tax rates—that maximize the sum of the utility payoffs (happiness levels) of the people is now known as utilitarianism. What is important for our discussion about fairness is that the property of diminishing marginal utility is closely related to the ethically pregnant concept of relative neediness.
To see this, suppose that everyone derives more utility from their first $10,000 of income more than from their second $10,000 because the first $10,000 permits them to buy those staples their families need most, for example, basic food and rent. It is then an easy stretch to argue that a poor family with a total income of $30,000 “needs” its entire income to acquire the staples every family needs much more than a rich family with $300,000 of income does. If this is so, then a tax code that maximizes the public good will necessarily be progressive, and the rich will have a higher tax rate than the poor. This can be shown formally. In sum, a progressive tax code is much more consistent with the principle of to each according to his need than, say, a flat tax rate is.
Needs-Based Arguments for Redistribution
The four ways we have seen in which issues of fair distribution arise within economic theory bring us to the doorstep of the fifth way they arise outside of economic concerns. There is now an increasing demand for a no-holds-barred moral philosophical analysis of what distribution of wealth and income is fair, and why. In the debate over this issue, there has been a bias towards needs-based fairness as opposed to contribution-based fairness. More specifically, greater need on the part of the poor has been the touchstone for the theories of philosophers like the late John Rawls of Harvard. Rawls’ magisterial Theory of Justice created an explosion of interest in the topic of distributive justice when it was published in 1971.13
Following Rawls, and the utilitarian logic sketched previously, most philosophers have championed strongly redistributionist policies based upon the primacy of need by the poor. Furthermore, their attention has shifted from classical issues of how to fairly fund public goods to much deeper issues. For example, philosophers now question whether the highly unequal initial endowments of wealth and skills that people enjoy are “morally arbitrary” as Rawls called them, or not. If they are arbitrary and undeserved, then why not force wealth and income transfers to rectify the unfair starting point caused by unequal endowments? After all, the Second Fundamental Theorem of Welfare Economics sanctions doing so, with no loss of efficiency except for those incentive effects discussed earlier.
In another direction, the classical utilitarian criterion of selecting policies so as to maximize the sum total of human happiness has come under strong scrutiny because it is viewed as insufficiently redistributive. Indeed, Rawls’ entire theory was a rebuttal to utilitarianism on these grounds, and his conclusions about tax rates are more egalitarian. We now turn to this subject in the final section in the chapter.
In closing this discussion of economic fairness, it is worth remembering that Adam Smith himself viewed economics as part of moral theory, and more generally of the Science of Man as he and his great friend David Hume dubbed their mutual investigations. Moreover, he had strong personal views about distributive justice, as any civilized person does. For example, he did not believe in inherited wealth, and he had little use for highly unequal distributions of income. In today’s language, he thus believed in confiscatory inheritance taxes, and in highly progressive income tax rates. Imagine: Adam Smith of all people!
A Comprehensive Theory of Distributive Justice
For the 1992 Handbook of Game Theory, one of a number of volumes constituting the Handbook of Economics edited by Kenneth Arrow and Michael Intrilligator, John Harsanyi was asked to write the chapter on the subject of ethics, with a particular focus on distributive justice. His mission was to show how the advent of decision theory and game theory had impacted moral philosophy, and had made possible several overarching new theories of social justice.14 Harsanyi was chosen to write this essay because he was the only game theorist who was also a moral philosopher and had made fundamental contributions to the theory of utilitarianism.
In his Handbook essay, he reviewed and contrasted three quite different theories of justice: utilitarianism, Rawls’ theory, and a third quite formal theory that I developed in the late 1970s upon completing my PhD dissertation at Princeton.15 Since this third theory was developed after the first two theories, I attempted to clarify several of the earlier arguments, and to extend moral theory in a new direction. Let me use a diagram taken from my original 1978 paper to clarify some of the issues involved, and to permit a comparison of the three theories. The issues here are utterly fundamental, very relevant today, and intrinsically interesting. Also, as with the results in Chapters 2–5, the logic utilized is strictly deductive in nature.
A “supergame” in game theory is just a game consisting of other games known as subgames. In Figure 6.1, the topic of distributive justice is modeled as a two-stage supergame. In the stage 1 game, members of society adopt some constitution setting forth the basic laws under which they will live. This constitutional choice problem can be thought of as that of selecting a set of “basic institutions” or equivalently an “incentive structure” that will constrain behavior in the second stage game. Then in the stage 2 game, people get jobs, compete, and do what is best for themselves and their careers. But in doing so, they are subject to the laws of the constitution selected in the stage 1 game. The black rays within each regime box indicate the set of all real-world strategies from which members of society will choose their best strategies during the stage 2 problem.
Figure 6.1 Modeling the Constitutional Choice Problem
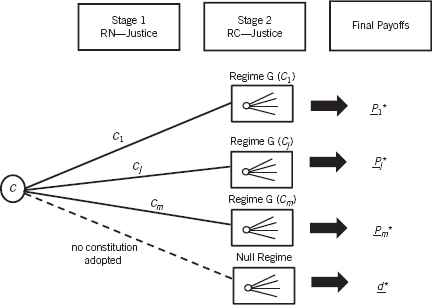
Appearing on the far right of the figure are the “payoffs” to everyone from doing what is best for himself or herself subject to the provisos of the constitution adopted. The capitalized letter P underlined is just shorthand for the fact that P consists of n different payoffs when there are n people involved, with one payoff specified for each person. Thus P = (P1, P2, P3, . . . Pn). There is one last detail. The dotted line at the bottom leading to a “null regime” with payoff d represents what happens if the citizens fail to agree on any constitution at all. This regime represents a noncooperative game in the sense of Chapter 5. Its payoff d can be thought of as the payoff from a Hobbesian world devoid of laws and basic institutions, in effect a free-for-all of the kind witnessed today in Somalia.16
One assumption common to all three theories is that the payoffs P from all regimes possessing constitutions are high enough to permit all players to end up better off than they would be with payoff d in the null regime. This is not a restrictive assumption since, in a cooperative game, side-payments can be made from winners to any losers in all the games with payoffs P. That is, the gains from cooperation of all those who benefit from the adoption of a constitution will far exceed any losses to losers, and the latter thus can be compensated via side payments.
Following in the footsteps of classical social contract theory, all three theories of justice that Harsanyi reviews adopt a two-stage structure like the one in our figure. For a real world example of this kind of social choice problem, consider the Constitutional Convention of 1787 when the U.S. constitution was hammered out in the summer heat of Philadelphia. Once adopted, its provisions would constrain behavior throughout society by setting out just what kinds of laws, tax rates, and penalties could be enacted.
The Two Fundamental Norms: Needs and Contribution
What moral norms should be respected in each of the two subgames pictured here? I took my cue from a paper sent to me by Professor Daniel Bell in 1976, a celebrated Harvard sociologist interested in issues of justice. The paper was by the Oxford philosopher Charles Taylor who stated something that neither Rawls nor the utilitarians had been explicit about: the requirement that any acceptable theory of justice must take account of both needs-based and contribution-based fairness. The importance of these two norms was stressed by Marx, and Rawls recognized the merits of both.17 But neither Marx, nor Rawls, nor the utilitarians paid more than lip service to “to each according to his contribution.” Needs-based justice always predominated, and everyone acknowledged that it was hard if not impossible to reconcile the two norms.
In this vein, recall Marx’s memorable imperative: “From each according to his ability (ability to contribute), to each according to his need.” The key phrase here is “. . . to each according to his need.” The fruits of those who contribute more are presumably to be seized for those of lesser abilities who are more needy. Of course, those who contribute more may not like being used as pack horses for others, and might just decide to withhold their capital and labor so that less is left over for the needy. Indeed, it would be rational for them to do so, as Aumann and Kurz proved in their “Power and Taxes” paper cited earlier.
Unification of the Two Norms within a Comprehensive Theory
I did not accept the view that the conflict between these two different principles of distributive justice was intractable, and agreed with Professor Taylor that a proper theory of justice must accommodate both norms within a unified theory. In my theory, I argued that needs-based justice is appropriate in the stage 1 problem of constitutional choice, whereas contribution-based justice is appropriate in the stage 2 game of real life. The labeling in Figure 6.1 should make this clear.
Why might this be true? First consider the nature of the stage 1 game. There is an opportunity for everyone to benefit by agreeing upon the basic institutions required for a political economy to function well. No one contributes more than anyone else in this game, a game in which no actions of any kind enter the picture. Rather, what is at stake are the mutual gains made possible by agreeing upon a set of basic institutions at a constitutional convention. These institutions in turn make possible in the real-world stage 2 game the existence of an impartial rather than a biased judiciary, a progressive rather than a regressive tax code reflecting the differing abilities of people to pay, and an overall sense of fairness required for social cohesion and peace.
Some philosophers have deemed the ability of all members of society to gain from agreement on such basic institutions to be “manna from heaven.” No claim based upon differential contribution can be made for this manna. Its existence is God given, just as is the possibility of enjoying a beautiful sunset, using waterfalls to generate power, or utilizing mass to create energy via Einstein’s celebrated equation E = mc2. The only way one member might contribute more than another in the stage 1 game lies in better conceiving and articulating the possibilities of constitutional choice than another does. But this particular talent seems irrelevant to the ultimate choice of a constitution. Overall, in manna contexts where no one contributes more or less than another, distribution according to relative neediness would seem to be the only morally acceptable criterion to invoke in arriving at the choice of a constitution. This conclusion is seen in the labeling of the two stages of the supergame in Figure 6.1.
Note that in speaking of a constitution, I refer to a set of “basic” institutions, not the set of all possible institutions. This is an important proviso. For the constitutions to be chosen from in stage 1 must be sufficiently minimalist in their constraints to permit sufficient freedom and flexibility required in the real-world stage 2 game. It would thus be counterproductive in stage 1 to determine who eats or wears what in the real-world setting of the stage 2 game. Agents in the stage 1 game know this, and know that they will value freedom in the real-world game. They thus settle upon a liberty-respecting constitution.18
Now consider the real-world stage 2 regime. The situation here is opposite to that in the stage 1 game. Here, individuals do contribute differentially to the creation of businesses, to writing books, to running restaurants, or other worldly activities. Here it is all about which team player is MVP, which firm had the highest return on the capital of savers/investors, which restaurants gained the highest recognition, and so on. In this real-world competitive context, distribution according to relative contribution is the appropriate moral criterion.
It is here in stage 2 that those virtues of the free-market system demonstrated by Hurwicz come into full bloom, virtues generated by the ability of agents to focus selfishly on maximizing their own risk-adjusted returns. And by extension, it is here that contribution-justice takes center stage (who is the MVP?), and that issues of needs-justice do not and indeed should not arise. Market behavior will not be efficient if agents are altruistic during their 8:00 a.m. to 5:00 p.m. jobs and focus on matters other than running their businesses to maximize returns. They can, of course, be altruistic after hours, as most of us are when we are with friends and family, or are assisting charitable activities.
Does this seem somewhat cold-hearted? In fact, it is not. This is because everyone knows during their 8:00 to 5:00 hours of self-interested behavior that issues pertinent to relative needs have already been addressed and dealt with by suitable provisos in the constitution chosen in the stage 1 game. These are the reasons why my theory requires that distributive justice in the stage 2 game respects relative contribution. In economic terms, the pretax remuneration to all agents should be in proportion to their marginal contributions.
What is remarkable in this regard is that the payoff from competitive market behavior under almost any constitution will automatically satisfy contribution-justice. Even more remarkably, in any non-market or political context where multilateral bargaining behavior is involved, the outcome will also respect the relative contribution principle. Both of these results follow from Robert Aumann’s remarkable 1977 theorem cited previously.19
Overall, what this theory does is to disentangle the two fundamental distributive norms cited by Professor Taylor and apply them in the two totally separate domains where each is relevant. Needs-justice governs the choice of basic institutions and tax rates in the stage 1 game, whereas contribution-justice operates within whatever stage 2 game results from the constitution chosen. There is thus a clear division of labor between these two dimensions of moral theory.
The Princeton Philosophy Department
I tested these basic ideas in a case study I developed when I was a graduate student at Princeton years ago. Suppose the university’s eminent Department of Philosophy must choose between two excellent professors in awarding tenure: Susan Stentley and Tom Smith. Both have done excellent work, but Susan is thought to have a very slight edge professionally. Yet there is a complication. Tom is the more affable and popular colleague, and has an expensive illness as a result of which he would benefit much more than Susan from the added income and job security the tenured position would make possible. Which candidate will Princeton choose? Which should it choose?
The answer I received from every professor I asked—and most had very liberal views—was that they would pick Susan. “Our primary responsibility is to hold this department to the very highest academic standards possible.” In my theory, this ostensibly heartless reply will be morally acceptable provided that the basic institutions of society chosen in stage 1 fund the cost of Tom’s illness. This is the division of labor I just spoke of. To sum up, during their stage 2 game, the Princeton philosophers focus on the quality of their department and its reputation, and contribution-justice prevails. But they do so knowing that the most basic needs of their colleague Tom have been dealt with “elsewhere,” via provisions of the constitution arrived at during the stage 1 game.
How to Measure Relative Needs
In both Rawls’ theory and in Harsanyi’s version of utilitarianism, the concepts of relative need and relative contribution remain somewhat murky. But why shouldn’t they? Knowing how to measure and quantify both concepts has been a notoriously difficult problem for centuries. Peyton Young only determined how to correctly measure relative contribution in 1988, as already noted. Assessing relative needs is arguably more difficult than relative contribution. The reason is that doing so seemingly requires us to make what are known as “interpersonal comparisons of utility,” or interpersonal comparisons of well-being to put it more colloquially. Let me further explain this difficulty.
Suppose Mother Teresa wishes to distribute $1 million between 20 supplicants of different needs, and suppose she wishes to do so in accord with the principle of relative need, as seems most reasonable.20 Now how can she do so without an absolute yardstick of well-being whereby she can compare how much absolute well-being each claimant receives from each marginal dollar awarded? Who benefits the most? The second most? The third most? Rawls’ theory requires a very basic comparison along these lines, and utilitarianism requires a much more demanding type of interpersonal comparison.21 Many philosophers and economists object strenuously to the need to make such interpersonal comparisons since no one knows how to make them. This has always been a fundamental problem in moral theory.
The good news is that progress has been made in resolving this difficulty. In the case of relative needs, after being challenged by this issue for over 20 years, I demonstrated in 2004 that there is a unique measure of relative neediness that satisfies seven axioms. Remarkably, no interpersonal comparisons of utility are needed to arrive at this measure.
The result followed from discovering and proving that “relative risk aversion” so crucial in bargaining theory is formally equivalent to “relative neediness” in moral theory. Since bargaining theory awards pieces of pie in inverse proportion to relative neediness (the more risk averse you are, the more you get bargained down), the result implies that the relatively more needy you are, the less you receive. It thus turns out that the inverse of the ratio of sizes of the two pieces of pie awarded by bargaining is the appropriate measure of relative need. Finally, since no interpersonal comparisons of utility are needed in the Nash-Harsanyi theory to determine the sizes of the slices of the pie awarded by bargaining, none are required to determine relative neediness measured in this way.
To see this more clearly, suppose you get two-thirds of the pie and I receive one-third from bargaining. Given the logic just reviewed, the only reason for the outcome awarding twice as much pie to you as to me is that I am twice as risk averse—and equivalently twice as needy—as you are. Thus from a needs-based ethical standpoint, I should get twice as much as you do. Accordingly, the ethical allocation “flips” the bargaining allocation and I receive two-thirds of the pie, and you only one-third.22
Full Distributive Justice and a Theory of the State
If the supergame introduced in Figure 6.1 is solved, the result is full distributive justice in my theory. The two fundamental distributive norms of contribution and need are satisfied in the right order, in the right place, and in a very precise manner. Each applies in the context where it should apply, and there is no incompatibility between them. As a bonus, no interpersonal comparisons of utility are called for.
There is one last detail. The stage 1 game as I have described it is not in fact a game proper, but rather an arbitration scheme whereby a group of “founding fathers” collaborate to arrive at the fairest possible constitution. The decision problem within stage 2 is of course a genuine game. Thus it might seem that the supergame in Figure 6.1 is not in fact a supergame proper, but a hybrid of sorts. This is not in fact the case. For in determining the relative needs respecting constitution sought in the stage 1 problem, a particular Nash-Harsanyi bargaining game must in fact be solved, for the reasons described in endnote 22. So my construct can be viewed either as an arbitration problem, with an embedded stage 2 game, or else as a proper supergame. There is one last surprise: the two formulas for determining allocations that satisfy “to each according to his relative need” and “to each according to his relative contribution” are themselves very closely related, the one being dual to the other.23
Comparison with Rawlsism and Utilitarianism
All three theories make use of an “original position” or “veil of Ignorance” or constitutional convention in which basic rules of the game are selected before we go out and play the game of life. So do most all historical theories of the social contract, for example, those of Rousseau and Locke. What the new theory offers is crystal clarity about previously murky concepts (“constitution,” “needs,” “contribution”). Additionally, ethics becomes free of the necessity of making interpersonal comparisons of utility. Finally, the theory does appropriate justice to both Relative Needs and to Relative Contribution.
Where these three theories differ significantly is in their treatment of the concept of relative needs. Rawls’ stage 1 game, or his “original position” as he calls it, is one where every agent is assumed to be completely risk averse in the following sense: In the original position, every agent focuses exclusively on obtaining sufficient “primary goods” that he and his family can survive. Getting the minimal standard of living these goods bestow is of such momentous importance that he places no value at all upon upside risk, that is, upon the chance of ending up with more than his bundle of primary goods. An equivalent way of stating this is that everyone in the original position is assumed to act as if he was certain that he will be poor, blind, and disadvantaged when he exits the original position. These strong assumptions lead people to select a constitution which is very egalitarian.
Harsanyi and many others viewed Rawls’ exclusion of consideration for everyone except the worst-off members of society as confused and invalid. In his resurrection of utilitarianism, Harsanyi introduced a different and far more compelling scheme. Everyone in his original position is under a veil of ignorance. Everyone is ignorant as to what his characteristics will be when the stage 2 problem gets played, for example, poor and blind versus rich and well-sighted. More specifically, everyone is assumed to have an equal chance of ending up in anyone else’s shoes. When a constitution is chosen under these assumptions, Harsanyi proves that it will be the one that maximizes the greatest good, or equivalently, it will be the utilitarian solution.
Harsanyi comes very close to arguing that the utilitarian outcome satisfies the norm of Relative Needs. And to an extent, it does. This is because of the role of diminishing marginal utility already discussed. We saw how utilitarianism logically implied a progressive tax code for this reason. Nonetheless, Harsanyi never clearly defined Relative Neediness, and did not show formally that the utilitarian decision rule does in fact allocate goods in proportion to relative neediness.
It has now been proven that the utilitarian allocation does not in fact satisfy the Relative Need norm, as my own theory does. Nevertheless, it can be shown that the prescriptions of the two theories will differ very little in many practical applications. Rawls’ theory for its part is not consistent at all with Relative Need. Rather, he focuses on the absolute needs of the worst off.24
In writing this highly ambitious chapter, I hope I have been able to convey a sense of marvel at the progress that has been made in recent decades in clarifying a number of age-old concepts such as the nature of an ideal society, the status of democratic capitalism, and the meaning of justice in distribution. On the economic front, the work of Leonid Hurwicz arguably represents the most important step forward, since he dramatically generalized both the context and the concepts of classical economic theory. Nonetheless, while Hurwicz understood the importance of distributive justice as an important norm in the design of a social system, he wrote little about the subject and did not provide a theory of justice of his own. Interestingly, no economist has done so in recent decades. To be sure, scholars such as Arrow, Bergson, Samuelson, and Scitovsky greatly refined the quasi-ethical concept of the social welfare function introduced a century earlier by the utilitarians. But none of these economists produced an actual theory of distributive justice.
Two people did: John Rawls and John Harsanyi. It is these two who deserve credit for revitalizing this topic by introducing decision-theoretic arguments permitting concrete results about the nature of a fair distribution of wealth and income. This represented a milestone in the development of moral philosophy. Other nondecision-theoretic approaches have been advanced to clarify issues of distributive justice, but I have not found these compelling. For example, Harvard philosopher Thomas Scanlon published an important book on justice entitled What We Owe to Each Other in 1998.25
In his theory, Scanlon eschews the use of the highly analytic approaches reviewed in Harsanyi’s Handbook of Game Theory article cited earlier. Rather, as is fashionable in current moral philosophy, Scanlon provides a very thoughtful if complex “account” of issues that arise in moral theory. What is odd is that, after reading his book, I had no idea how Scanlon would solve the simplest of all distributional problems, for example, how Mother Theresa should divide a pie “fairly” between people of different degrees of neediness. Indeed, Scanlon seems unaware that great progress has been made on this front
In the real world, decisions of just this kind must be made regarding what we really do owe to each other. In this regard, it is not surprising that the advent of decision theory and game theory has provided a tremendous assist to moral and political theory by permitting it to ascend from the murky level of philosophical “accounts” and word games about classical problems to the level of solutions applicable in the real world. This is the message I have tried to convey in the concluding part of this chapter.