The Mayan Factor

APPENDIX A. RADIAL AND DIRECTIONAL NUMBERS

The richness of the radially reciprocal understanding of the thirteen numbers is further amplified if the individual numbers in the series 1-13 (or 13-1) do not have simply a sequential but a directional relation to each other as well. In other words, let the first number 1 represent the East; the second number 2, the North; the third 3, the West, and the fourth 4, the South; and the fifth 5, the East again, and so forth. The series 1-13 with directional notations would now look like this:

1	-	2	-	3	-	4	-	5	-	6	-	7	-	8	-	9	-	10	-	11	-	12	-	13
E	-	N	-	W	-	S	-	E	-	N	-	W	-	S	-	E	-	N	-	W	-	S	-	E

Arriving at 13, the pulsation returns to 1, while the directional notations continue where they left off:

1	-	2	-	3	-	4	-	5	-	6	-	7	-	8	-	9	-	10	-	11	-	12	-	13
N	-	W	-	S	-	E	-	N	-	W	-	S	-	E	-	N	-	W	-	S	-	E	-	N	etc.

In order for 1 to be matched with Eagain, there will have to be 52 pennutations(13 numbersx4directional positions). Let us also say that the directional positions have their own cycle which consists of 5 rounds, in other words the E-N-W-S pattern must spin 5 times in sequence to complete a single cycle for a total of 20 positions—20 of course, being not only 4x5 but the sum of 7 and 13, the two key "mystic" numbers in the series 1-13.

This being the case, a radial matrix is created in which there are a total of 260 possible permuations—the Tzolkin—described by the spinning of the 13 numbers each one revolving through 20 possible directional positions. If the 13 numbers are each accorded a particular tonal quality given variation by the 20 positions, then through all the possible permutations a rich harmonic description becomes possible. The 260-unit matrix might begin to look like a multiphasic keyboard for the composition of the galactic symphony—which indeed it is!

APPENDIX B. MAYAN FACTORS & FRACTALS

To understand fractals, just remember: a fractal is a proportion that remains constant. For instance, a 36-degree segment of a circle will always be 36 degrees no matter how large or small the circle. Also, in this segment of a circle sufficient information is contained to allow one to construct the whole circle. The fractal principle underlies the holographic nature of things: from one fraction of a particular whole, the entire whole can be constructed.

The same principle applies to overtones. Just as atone in one octave may be reverberated or sounded at other octaves, though the different octave tones vibrate at different frequencies so a number or a fraction of a number set may be "sounded" at many different levels yielding similar proportional overtones. Incidentally, when a 16-tone scale is sounded, only one tone reverberates a rich matrix of overtones—the thirteenth.

For instance: 13 is a fractal of 130 (13 x 10), 144 is a fractal of 1,440 (144 x10); that is, from the 13 we may construct the 130, or vice versa, while from the 1,440, we may derive the 144. In this case, the fractals 13 or 144 represent proportions that remain constant through a potentially infinite series.

Thus, a fractal tonality can be set up with a whole range of numbers: 26, 260, 2,600, 26,000 etc. or 52, 520, 5,200, 52,000, etc. What is important and gives the tone to each of the numbers in a fractal series is not the quantity, which the number most certainly also denotes, but the key fractal number itself, i.e., 13,26,52, etc., which creates the proportional "tone" in the series. The zeros added to a fractal series may be taken as the equivalent of higher registrations of frequencies.

Related to fractals are factors—the numbers which provide the multiples of a given figure, i.e. 260 is the product of the factors 13 and 20. At the same time, 260 is a member of the fractal series based on 26. 26 itself is the product of 13 and 2. All fractals are factoral numbers which provide the basis for different series of proportional relations.

Patient reflection will show how the different numbers interpenetrate and pervade each other like different kinds of perfume. For instance, 144 would always be read as 12x12, 9x16, 18x8, 3x36, or 72x2; while 52 would be read as factors of 13x4 or 26x2. Incidentally, in the Mayan system virtually all of the key fractals are factors of either 13, 4, or 9. Thus 260 is a factor of 13x20; 64 is a factor of 4x16; and 144 is a factor of 9x16. In this way various larger whole numbers are considered more or less harmonic according to the diversity of the factoral and fractal possibilities which they represent.

APPENDIX C. CALENDAR HARMONICS

The 360-unit "calendar" called the tun represents the third positional rank of the Mayan number progression which utilizes the factor of 9. This progression, which otherwise proceeds by multiples of 20, could go on infinitely, but for practical purposes consists of nine orders. Read from bottom up, with the Mayan names for the respective positional places and time approximations, the nine orders are:

9. Alautun = 23,040,000,000 (or 20 kinchiltuns) 63,040,000 + years

8. Kinchiltun = 1,152,000,000 kin (or 20 calabtuns) 3,152,000 + years

7. Calabtun = 57,600,000 kin (or 20 pictuns) approx 157,600 + years

6. Pictun = 2,880,000 kin (or 20 baktuns) approx 7,900 + years

5. Baktun = 144,000 kin (or 20 katuns) approx 394 + solar years

4. Katun = 7,200 kin (or 20 tuns) approx 19 + solar years

3. Tun = 360 kin (or 18 (9 x 2) vinals) approx 1 solar year

2. Vinal = 20 kin (or 20 days)

1. Kin = 1kin(or1day)

Had this progression moved purely by 20s, a tun would be the equivalent of 400 kin. Instead, the factor of 9 is introduced in the order of vinal, the 20-day periods. Instead of 20 vinal there are only 18. Hence, 18x20-360 kin or one tun. The rest of the progression continues by moving in multiples of 20s, but stained, as it were, by the warp caused by the introduction of the factor of 9 in the second order.

The preceding progression of nine orders is the count the Maya adopted for purposes related to computations of time. Hence, 9 is the number most closely associated with the concept of time. In any case, this progression utilizing the warp of 9 is in contrast to the Mayan "pure" count. While our positional mathematics is decimal, that is, advancing by 10s, the Mayan "pure" count is vigesimal, advancing by 20s. While our system advances 1, 10, 100, 1,000, etc, the Mayan advances in the following manner:

9th Position: one unit equals 25,600,000 (20x1,280,000,000)

8th Position: one unit equals 1,280,000,000 (20x64,000,000)

7th Position: one unit equals 64,000,000 (20x3,200,000)

6th Position: one unit equals 3,200,000 (20x160,000)

5th Position: one unit equals 160,000 (20x8,000)

4th Position: one unit equals 8,000 (20x400)

3rd Position: one unit equals 400 (20x20)

2nd Position: one unit equals 20 (20x1)

1st Position: one unit equals 1 (1x1)

It should be noted that the fractal numbers of the Mayan pure progression—2, 4, 8, 16, 32, 64, etc.—represent the binary progression that proceeds by doubling the last sum, i.e, 2+2=4, 4+4=8, 8+8=16, etc. This progression underlies the permutational mathematics of both DNA and the I Ching.

But to return to the "calendar" and its numbers, as noted, in the 260-and the 360-unit "calendars" we see the key numbers: 4, 9, and 13.4 is the number signifying measure; 9 is the number signifying periodicity or completeness; 13 is the number signifying the movement immanent in all things. The difference between 9 and 13 is, of course, 4.

While 7, midway between 1 and 13 is the mystic open term that penetrates all things, 5, the difference between 4 and 9, is the number of the center understood as the point from which things can be measured, i.e., the four directions, the seasons etc. This is because 5 is 4, the number of measure, plus 1, the number of unity.

The meaning of any number depends partially on the factors of which it is the sum. 2 (1+1) is the number signifying polarity, while 3 (2+1) represents the principle of rhythm. 6 (3x2 or 3+3) is the number of rhythmic wholeness, while 8 (4+4), or "measure" doubled, is the number of the octave, the key resonant harmonic number itself. 10 (9+1) represents the principle of manifestation; 11, the principle of dissonance; and 12, the principle of dynamic stasis.

APPENDIX D. HARMONIC NUMBERS

The principle of the harmonic number, as stated in Appendix B, is that larger whole numbers are considered more or less harmonic according to the diversity of the factoral and fractal possibilities which they represent. 936,000, representing the midpoint of the Great Cycle, is an example. Marking as it does the passage of six-and-one-half cycles of 144,000 kin or days each, the number 6.10.0.0.0 denotes harmonic 936, the passing of 936,000 (6.5x144,000) days or kin from the initiation of the cycle in 3113 B.C. In addition, 936,000 accommodates the key fractal 26 in that 936,000 = 2,600 tun of 360 days each. Numerologically, the date 936,000 kin (9+3+6=18=1+8) equals 9, as do all factors of 9.

The greatest harmonic number, however, is 13 66 560:

13 66 560 divided by 360 = 3796 Tun (tun = 360 kin).

13 66 560 divided by 365 = 3744 Haab (365 kin = Haab, or solar year).

The difference between 3796 Tun and 3744 Haab = 52 (13x4). 52 = a "calendar round" of 52 solar years synchronized with 73 sacred calendar cycles of 260 days each.

13 66560 divided by 72 = 18980, the number of days in a 52-year "calendar round."

A 52-year calendar round = 52 x365 or 260x73.

13 66560 divided by 73 = 18720 = 52x360 or 260x72.

13 66 560 divided by 9, number of the Lords of Time = 15 1840.

151,840 kin divided by 365 = 416 vague solar years (Haab).

13 66 560 divided by 260 = 5256 Tzolkin or sacred calendar cycles.

13 66 560 divided by 584, apparent days in Venus cycle = 2340 Venus years.

13 66560 divided by 780 apparent days in a Martian cycle = 1752 Mars years.

13 66 560 divided by 2920 days = 468 Venus-solar cycles.

2920 divided by 365 = 8; divided by 584 = 5.

13 66 560 divided by 37960 = 36 cycles of 104 years; 104 years corresponds to one conjunction of the Venus, sacred calendar, arid solar cycles.

13 66 560 divided by 52 = 26 280 or 72 vague solar years.

13 66 560 divided by 12 = 1 13 880 or 312 vague solar years.

13 66 560 divided by 13 = 10 51 20 or 288 vague solar years.

13 66 560 divided by 8 = 17 08 20 or 468 vague solar years.

While we will go into detail later regarding the significance of some of these abovementioned cycles—the calendar round and the Venus cycles in particular—it is sufficient here to merely contemplate the amazing capacity of the harmonic 136656 to accommodate so many different factors and cyclic figures.

If we are to take the number 13 66 560 as the number of days from starting point 3113 B.C., we arrive at 9.9.16.0.0 or A.D. 631. This date is the equivalent of 3796-tun cycles of 360 days each or 3744-haab or solar cycles of 365 days each. The difference between the 3796-tun and 3744-solar cycles from the date 3113 B.C. is 52. If we add 52 years, the number of years in a "calendar round," to the date 9.9.16.0.0, A.D. 631, we arrive at the date 9.12.8.13.0, or A.D. 683. The number of days elapsed from 3113 B.C., the commencement of the Great Cycle, to A.D. 683, is 1385540, or the equivalent of 3796 vague solar years—vague because leap-year days are not included. The number 13 85 540 also corresponds to 73 52-year calendar round cycles. 73 is the number of 260-day Tzolkin cycles that synchronize with 52 solar years to comprise a calendar round (52x365=260x73). Thus the date A.D. 683 would correspond to a calendar round fractal overtone. On the other hand, 13 66 560 or A.D. 631 also corresponds to 73-tun cycles of 52x360 units. Small wonder that Pacal Votan would be associated with the magnificent number 13 66 560!

Finally, 13 66560 corresponds to the completion of the 36th solar-Venus cycle (each of 104 years—l04x36=3744 solar years) since the commencement of the Great Cycle, 3113 B.C. As both the morning and the evening star, Venus is the planet especially associated with Quetzalcoatl-Kukulkan. For Quetzalcoatl was both Lord of Dawn, bringer of light, the morning star, and Guide of the Dead, presider over the mysteries of the dead, the evening star.

APPENDIX E. THE 52-YEAR CYCLE & DAILY CALENDAR ROUND

The Tzolkin, understood as the 260-day Sacred Calendar, when combined with the 365-day vague solar calendaror Haab, creates a cycle of 52 years. That is, the coincidence of day one of the Sacred Calendar and day one of the solar calendar occurs only once every 18,980 days or approximately 52 years. While the 260 days repeat endlessly, the 365-day Haab is divided into 18 Vinal of 20 days each with as-day VAYEB or clean-out period preceding the beginning of another year. Thus, a traditional Mayan date always includes a date from the 260-day cycle as well as one from the Haab, for example: 2 IK 13 ZOTZ, 13 AHAU 1 POP, etc.

52 (13x4, 26x2), 1/5 of the 260-unit Harmonic Module is clearly a key Mayan number; it also appears in the Great Seal of the United States of America (13 arrows, 13 stars, 13 stripes, 13 olive branches). Obviously, the 52-year cycle is a fractal of the 5,200-tun Great Cycle, approximately 100 52-year cycles constituting a Great Cycle. Among the later Maya, and especially the Aztecs, the 52-year cycles assumed paramount importance. At the time of the Conquest, the 52-year cycles were counted from the day 1 Reed, the Year 1 Reed, which happened to be the date Cortes landed in Mexico. This date concluded thirteen 52-year heaven cycles and commenced nine 52-year hell cycles, which complete themselves August 16, 1987.

Part of the elegance of the 52-year cycles and the coordination of the 260-day Tzolkin with the365-day Haab is that the beginning point of each of the 52 vague solar years in this cycle can only fall on one of four Sacred Signs in a sequence that recapitulates the counter-clockwise directional rotation. These signs and their sequence are: MULUC (East); IX (North); CAUAC (West); and KAN (South). The Mayan year currently begins on the equivalent date, July 26. July 26, 1986, was the date 7 MULUC; July 26, 1987, is the date 81X; July 26, 1988 is 9 CAUAC, etc. On leap years, there are six instead of five Vayeb. The Vayeb always fall on the five (or six) days prior to a POP. The first day of the Haab is always OPOP; i.e. July 26 is always O POP. The first day of a Vinal is always O, the last day 19.

The 18 Vinal plus the Vayeb and their glyph signs are given below. From this information, along with the planet-day sign concordances given below, it is easy to construct a day-book or calendar; and, given the information in Chapter 4, to begin to work with practical, everyday Mayan "astrology."

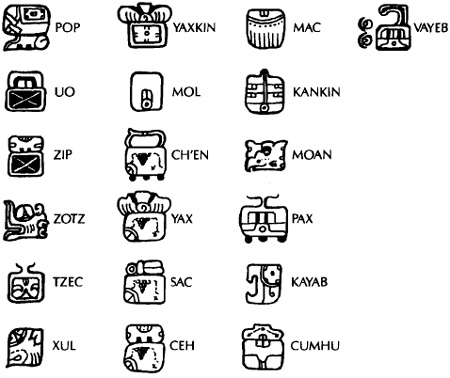
18 VINAL & VAYEB GLYPHS

CONCORDANCE OF 20-DAY SIGNS WITH PLANETS

IMIX—Solar Neptune

IK—Solar Uranus

AKBAL—Solar Saturn

KAN—Solar Jupiter

CHICCHAN—Solar A-Belt

CIMI—Solar Mars

MANIK—Solar Earth

LAMAT—Solar Venus

MULUC—Solar Mercury

OC—Galactic Mercury

CHUEN—Galactic Venus

EB—Galactic Earth

BEN—Galactic Mars

IX—Galactic A-Belt

MEN—Galactic Jupiter

CIB—Galactic Saturn

CABAN—Galactic Uranus

EDZNAB—Galactic Neptune

CAUAC—Galactic Pluto

AHAU—Solar Pluto

LIST OF YEARS, A.D. 1986-2012

GALACTIC SYNCHRONIZATION