“No” is only “yes” to a different question.
BOB PATTERSON
If every instinct you have is wrong,
then the opposite would have to be right.
JERRY SEINFELD
We encountered negations very early on while examining the law of the excluded middle and the law of noncontradiction. While Aristotle reminded us that it is impossible that the same thing both is and is not at the same time, he also recognized that we can construct both an affirmation and a negation that have identical meanings. Aristotle said that there are two types of propositions that are called simple—the affirmation, which is an assertion, and the negation, which is a negative assertion or a denial. All others are merely conjunctions of simple propositions.
“All humans are imperfect” is an affirmation, while “No human is perfect” is a denial with the same meaning. “Tuesday you were absent” is an affirmation, and “Tuesday you were not present” is a denial conveying the same information. “Four is not an odd number” is a true negation and “four is an even number” is a true affirmation expressing the same information from a different perspective. Inasmuch as it is possible to affirm the absence of something or to deny the presence of something, the same set of facts may be stated in either the affirmative or the negative.
So what does the negation of an “all” statement look like? Consider the negation of a simple sentence such as “All the children like ice cream.” Its negation might well read, “It is not the case that all the children like ice cream.” But even long ago Aristotle suggested that the negation be posed as the contradictory statement, such as “Not every child likes ice cream” or “Some children don’t like ice cream.” We could negate using the passive voice—“Ice cream isn’t liked by every child” or “Ice cream isn’t liked by some of the children.” The underlying structure of any of these negations is simply not (all the children like ice cream).
The noted logic historians William and Martha Kneale state that from the time of Parmenides in the fifth century B.C., the Greeks found something mysterious in negation, perhaps associating it with falsehood.1 In modern times, some researchers have argued that negation is not “natural” since it is hardly informative to know what something is not. However, more often than we may realize the only way to understand what something is is to have a clear understanding of what it isn’t. How would we define an odd number other than by saying it is a number that is not divisible by 2? What is peace but the absence of war?
Another argument put forth relative to the difficulty of reasoning with negation concerns the emotional factor. This position argues that the prohibitive nature of words such as “no” and “not” makes us uncomfortable. Some psychologists have suggested that since negation is fraught with psychological problems, negation necessarily increases the difficulty inherent in making inferences.2
Cognitive psychologists Peter C. Wason and Philip Johnson-Laird have written several books and dozens of articles on how we reason. They point out that negation is a fundamental concept in reasoning, a concept so basic to our everyday thinking that no known language is without its negative terms.3 Negation ought to be an easy, perhaps the easiest, form of deduction. However, making even a simple inference involving a negative is a two-step process. If I say, “I am not an ornithologist,” two statements must be absorbed. First, we must grasp what it means to be an ornithologist, then what it means not to be one. In our day-to-day communication, the extra step involved in reasoning with negation may well go unnoticed.
In one of their studies, Wason and Johnson-Laird performed a series of experiments focusing on the reasoning difficulties associated with negation. When asked questions that involved affirmation and negation, their subjects were slower in evaluating the truth of a negation than the falsity of an affirmation and got it wrong more often—a clear indication that negation is a more difficult concept to grasp.4
Negation may be either implicit or explicit. There is evidence that in some instances an implicit negative is easier to correctly process than an explicit negative. Implicit negatives are words that have negative meaning without using the word “not.” Implicit negatives, such as “absent” rather than “not present,” “reject” rather than “not accept,” and “fail” rather than “not pass,” may be easier to deal with than their explicitly negative counterparts. In other instances, implicit negatives may be too well hidden. For example, researchers have indicated that it is easier to see that the explicit negative, “The number is not 4,” negates “The number is 4” but more difficult to see that the implicit negative, “The number is 9,” also negates “The number is 4.”5
Researcher Sheila Jones tested the ease with which differently worded instructions were handled by individuals. Three sets of directions were tested that all had the same meaning—one set of instructions was an affirmative, one a negative, and one an implicit negative.6 The subjects were presented a list of digits, 1 through 8, and given one of the following sets of instructions:
Mark the numbers 1, 3, 4, 6, 7. (affirmative)
Do not mark the numbers 2, 5, 8, mark all the rest. (negative)
Mark all the numbers except 2, 5, 8. (implicit negative)
The test was set up in a manner similar to that shown in Figure 10. The subjects’ speed and accuracy were measured as indicators of difficulty. The subjects performed the task faster and with fewer errors of omission following the affirmative instruction even though the list of numbers was considerably longer. Subjects performing the task using “except” were clearly faster than those following the “not” instruction, signifying that the implicit negatives were easier to understand than the instructions containing the word “not.”

Figure 10. Task measuring the difficulty of the affirmative, negative, and implicit negative.
Some negatives do not have an implicit negative counterpart, and those negatives are more difficult to evaluate. The statement “The dress is not red” is harder to process than a statement like “Seven is not even,” because the negation “not even” can be easily exchanged for the affirmative “odd,” but “not red” is not easily translated. “Not red” is also very difficult to visualize. The difficulties involved with trying to visualize something that is not may well interfere with one’s ability to reason with negatives. If I say that I did not come by car, what do you see in your mind’s eye?
It may be that, wherever possible, we translate negatives into affirmatives to more easily process information. To make this translation an individual must first construct a contrast class, like the class of not-red dresses or the class of modes of transportation that are not-car. The size of the contrast class and the ease with which a contrast class can be constructed have been shown to affect our ability to reason with negatives.7
Wason and Johnson-Laird suggest that in everyday language a denial often serves as a device to correct a preconceived notion. Although it is true that I am not an ornithologist, I am not likely to make that statement unless someone was under the misconception that I was. The statement “Class wasn’t boring today” would probably not be made if the class were generally not boring. This kind of statement is usually made when the class is frequently or almost always boring. The statement functions to correct the listener’s previously held impression by pointing out an exception.
An experiment by Susan Carry indicated that negatives used on an exceptional case were easier than negatives used on unexceptional cases. In her experiment, individuals were exposed to and then questioned about an array of circles, numbered 1 through 8. All of the circles except one were the same color, and the circle of exceptional color varied in its position number. Presumably, most of us would remember the array of circles by remembering the exceptional circle since this requires retaining the least amount of information. Her experiment confirmed that it is easier to negate an exceptional case in terms of the property that makes it exceptional than to negate the majority cases in terms of the property of the exception.8
In addition, the results of a study by Judith Greene showed that negatives used to change meaning were processed more easily than negatives used to preserve meaning. Subjects were asked to determine whether two abstract sentences had the same or different meanings. A series of tasks paired sentences sometimes with the same meaning, one involving a negation and the other not, and other times paired sentences with different meanings, one involving a negation and the other not. Greene labeled a negative that signified a change in meaning natural, while a negative that preserved meaning was dubbed unnatural. For example, “x exceeds y ” and “x does not exceed y ” are easily processed by the brain as being different in meaning (thus the negative is performing its natural function), while “x exceeds y ” and “y does not exceed x ” are more difficult to assess as having the same meaning. Her studies support the notion that we more easily digest negatives that change a preconception rather than negatives that confirm a previously held notion.9
Aristotle went to great lengths in his treatises to point out that the negation of “All men are just” is the contradictory “It is not the case that all men are just,” rather than the contrary “No men are just.” In the negation, “It is not the case that all men are just,” the scope of the negative is the entire assertion, “all men are just.” The scope of the negative in the contrary “No men are just” is simply “men.” The difference between the contradictory and the contrary is that the contradictory is the negation of an entire proposition and that is why the proposition and its contradictory are always opposite in truth value. When one is true, the other is false, and vice versa.
Aristotle recommended that the statement “It is not the case that all men are just” was more naturally communicated as “Some men are not just.” Several studies have borne out the fact that this form may indeed be more natural. The smaller the scope of the negative, the easier the statement is to understand. Studies have shown that it takes systematically longer to process the type of denial involving “It is not the case that . . .” and “It is false that . . .” than ordinary negation. Indications are that statements where the scope of the negative is small, like “Some people do not like all ice cream flavors,” are easier to process than ones such as “It is not the case that all people like all ice creams flavors.”10
Medieval scholars of logic invented schemes and labels that became common terminology for students studying Aristotle’s classification of propositions. The universal affirmation, “All S are P,” was named a type-A proposition. The universal negation or denial, “No S are P,” was named a type-E proposition. This pair of A and E statements are the contrary statements. As such, they cannot both be true, but exactly one could be true or both could be false. The type-A universal affirmation, “All people are honest in completing their tax forms,” and the type-E universal denial, “No people are honest in completing their tax forms,” are contraries. In this case, both are probably false.
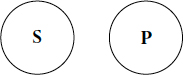
Figure 11. A Leibniz/Euler diagram of “No S are P .”
The Leibniz/Euler logic diagrams represent the universal negation, “No S are P,” as two spaces separate from each other—an indication that nothing in notion S is in notion P. The proposition, “No S are P,” is seen in Figure 11.
John Venn’s diagrams once again employed the use of overlapping circles to denote the subject and the predicate. In fact, all of Venn’s diagrams use the overlapping circles, which is one of its most attractive features. Using Venn’s graphical method, all of the Aristotelian propositions can be represented by different shadings of the same diagram—using one piece of graph paper, so to speak. Again, Venn’s shaded region indicates emptiness—nothing exists there. So in representing “No S are P,” the region where S and P overlap is shaded to indicate that nothing can be there, as shown in Figure 12.
Earlier, we witnessed the error in logic called conversion that is commonly made with the universal affirmative (type-A) proposition. It is a mistake to think “All S are P ” means the same thing as “All P are S.” Quite frequently one is true and the other is not. Just because all zebras are mammals doesn’t mean that all mammals are zebras. Yet, converting a type-E proposition (a universal negation) is not an error. “No chickens are mammals” and “no mammals are chickens” are both true. In fact, any time “No S are P ” is true, so is “No P are S.” This fact becomes crystal clear by looking at either the Leibniz/Euler diagram or the Venn diagram. In the Leibniz/Euler diagram, nothing in space S is in space P and nothing in space P is in space S. In John Venn’s diagram, nothing S is in P and nothing P is in S. Imagine what the diagrams for “No P are S ” would look like. Using either diagram, it is clear that the figure for “No P are S ” would look exactly the same as “No S are P ” with perhaps the labels on the circles interchanged.
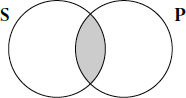
Figure 12. A Venn diagram of “No S are P .”
When No Means Yes—The “Negative Pregnant”
and Double Negative
In his On Language column, William Safire discussed a fascinating legal term called the negative pregnant derived from fifteenth-century logicians.11 The Oxford English Dictionary notes that a negative pregnant means “a negative implying or involving an affirmative.” If asked, “Did you steal the car on November 4?” the defendant replying with the negative pregnant “I did not steal it on November 4” leaves the possibility (maybe even the implication) wide open that he nonetheless stole the car on some day. Early on in life, young children seem to master this form of avoiding the issue. When asked, “Did you eat the last cookie yesterday?” we might well hear, “I did not eat it yesterday” or, “Yesterday? . . . No.”
Double negatives fascinate us from the time we first encounter them in elementary school. They cropped up earlier in the discussion of proofs by contradiction, where we begin by assuming the opposite of that which we want to prove. If I want to prove proposition P, I assume not-P. Proceeding by impeccable logic, I arrive at a contradiction, an impossibility, something like 0 = 1. What went wrong? My initial assumption must be false. I conclude, “not-P is false” or “it is not the case that not-P” or “not-not-P.” The equivalence of the statements “not not-P)” and “P”—that the negation of a negation yields a affirmation—was a principle in logic recognized by the Stoics as early as the second century B.C.12
All too frequently for the electorate we see double negatives in referendum questions in the voting booth. This yes-means-no and no-means-yes wording is often found in propositions to repeal a ban on something. A vote “yes” on the repeal of term limits means you do not favor term limits. A vote “no” on the repeal of the ban on smoking means you favor smoking restrictions. A vote “no” to repeal a ban on gay marriages means you favor restrictions on gay marriages, but a “yes” vote to repeal the ban on assault weapons means you do not favor restrictions on assault weapons. I recently received a ballot to vote for some proposals in the management of my retirement funds. The ballot question is in Figure 13. If you are like people who want their money invested in issues they favor (some folks don’t care), voting “for” means you are against gun control and voting “against” means you favor gun control.
Proposal: To stop investing in companies supporting gun control.
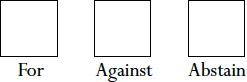
Figure 13. Example of when voting “for” means against.
Studies have shown that reasoners find it difficult to negate a negative.13 If the process of negation involves an extra mental step, a double negative can be mind boggling. Statements such as “The probability of a false negative for the pregnancy test is 1 percent” or “No non-New Yorkers are required to complete form 203” or “The statistical test indicates that you cannot reject the hypothesis of no difference” can cause listeners to scratch their heads (or give them a headache).
As we mentioned earlier, a statement like “It is not the case that all men are honest” is more naturally communicated as “Some men are not honest.” But some is not universal. So Aristotle defined propositions dealing with some are and some are not. Do they really need definition? You may be surprised to learn that they mean different things to different people. Read on.