If every boy likes some girl and every girl likes some boy,
does every boy like someone who likes him?
JONATHAN BARON,
Thinking and Deciding
Although statements about “all” of something or “none” of something are powerful and yield universal laws in mathematics, physics, medicine, and other sciences, most statements are not universal. More often than not, our observations about the world involve quantifiers like “most” and “some.” There was an important niche for nonuniversal propositions in Aristotle’s system of logic.
Ordinarily, if I were to assert, “Some parts of the lecture were interesting,” I would most likely be implying that some parts were not interesting. You would certainly not expect me to say that some parts were interesting if all parts were. However, the assertion “Some of you will miss a day of work due to illness” does not seem to forgo the possibility that, at some point or another, all of you might miss a day. Oftentimes, in everyday language, “some” means “some but not all,” while at other times it means “some or possibly all.” To a logician, “some” always means at least one and possibly all.
Whereas all and none are universal quantifiers, some is called an existential quantifier, because when we use some we are prepared to assert that some particular thing or things exist having that description. “Some” propositions are said to be particular in nature, rather than universal.
Much like the universal affirmative and negative propositions involving all and none, Aristotle defined and examined affirmative and negative propositions involving some. Whereas the universal affirmative “All people are honest” and the universal negative “No people are honest” cannot both be true, particular affirmations and their negative counterparts are oftentimes both true. The propositions “Some people are honest” and “Some people are not honest” are both most likely true. Medieval scholars named the particular affirmative proposition of the form “Some S are P ” a type-I proposition, and they named the particular negation of the form “Some S are not P ” a type-O proposition.
With the universal affirmative and negative propositions named A and E, respectively, students of logic used the mnemonic device—ARISTOTLE—to remember these labels. A and I propositions were affirmations and come from the Latin AffIrmo (meaning “I affirm”), and E and O propositions were negations from nEgO (meaning “I deny”).1 The outer two vowels, A and E in ARISTOTLE, name the universal propositions, while the inner two, I and O, name the existential or particular propositions. Medieval scholars also devised a diagram known as the Square of Opposition (Fig. 14) to illustrate the contrary or contradictory relationship between propositions.2 As seen in the diagram, A and E are contraries.
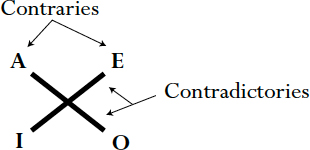
Figure 14. Square of Opposition.
The diagonals in the diagram represent the contradictories, A with O, and E with I.
Whereas John Venn used overlapping circles for propositions of any type (with different shadings), Gottfried Leibniz, and later Leonhard Euler, used overlapping circles only for expressing particular propositions. To illustrate “Some S are P,” the Leibniz/Euler diagram required the label for S be written into that part of S that is in P, whereas for Venn, an asterisk indicated the existence of something in S that is in P, as shown in Figure 15.3
Although the Leibniz/Euler diagram might look a little different if the proposition were “Some P are S ” (the P would be in the overlapping region instead of the S), the logicians themselves were well aware that in logic the two propositions are equivalent. Just as “No S are P ” and “No P are S ” are equivalent, “Some S are P ” and “Some P are S ” are interchangeable because their truth values are identical. If “Some women are lawyers” is true, then it is also true that “Some lawyers are women.” Venn’s diagram helps to illustrate this relationship. The asterisk merely indicates that something exists that is both S and P—as in “Some (one or more) people exist who are both women and lawyers.”
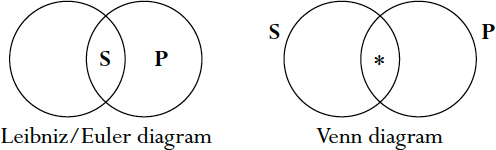
Figure 15. “Some S are P .”
However, in our everyday language we do not really use these statements interchangeably. We might hear “Some women are lawyers” in a conversation about possible career choices for women. The statement “Some lawyers are women” might arise more naturally in a conversation about the composition of the population of lawyers. Nonetheless, logic assures us that whenever one statement is true, the other is true, and whenever one is false, the other is false.
Every now and then, “some” statements seem rather peculiar, as in the statements “Some women are mothers” and “Some mothers are women.” The first statement is true because some (though not all) women are mothers. The second statement is true because definitely some (and, in fact, all if we restrict ourselves to the discussion of humans) mothers are women. But we must remember that, logically speaking, any “some” statement means “some and possibly all.”
For example, we would not normally say “Some poodles are dogs,” since we know that all poodles are dogs. During the normal course of conversation, a speaker likes to be as informative as humanly possible. If the universal “all poodles” holds, we generally use it.4 However, we might say “Some teachers are licensed” if we weren’t sure whether all were licensed. Author Jonathan Baron offers the example that when traveling in a new city we might notice that taxicabs are yellow. It would be truthful to say “Some cabs are yellow,” withholding our judgment that all are until we know for sure.5
An O proposition of the “Some are not” form can also be illustrated by two overlapping circles as in Figure 16. Venn’s diagram is clearly superior (in fact, the Leibniz/Euler diagram has some serious problems), since “Some S are not P ” and “Some P are not S ” are not interchangeable. Just because the proposition “Some dogs are not poodles” is true does not mean that “Some poodles are not dogs” is. In fact, it is false.
Peter C. Wason and Philip Johnson-Laird have performed studies that seem to indicate that individuals illicitly process “Some X are not Y” to conclude “Therefore, some X are Y,” believing they are just two sides of the same coin—in much the same vein as whether the glass is half full or half empty. But in logic the existential quantifier some means at least one and possibly all. If it turns out that all X are not Y, then “Some X are Y” cannot possibly be true. Their studies indicated that whether an individual gives the material this interpretation depends primarily on the material. Even though subjects were instructed to interpret some in its logical fashion, most were able to do so only with material that hinted at possible universality. For example, “Some beasts are animals” was interpreted to mean “Some, and possibly all, beasts are animals,” whereas “Some books are novels” was not generally interpreted as “Some, and possibly all, books are novels.”
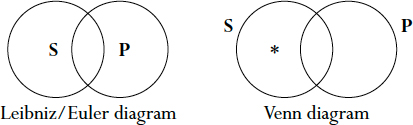
Figure 16. “Some S are not P .”
Might this be an indication that we are rational and reasonable after all? A computer could not distinguish between the contexts of these “some” statements in the way that the human subjects did. The subjects in these experiments were reading meaning into the statements given even though they weren’t really supposed to. Humans have the unique ability to sometimes interpret what another human meant to say. On the other hand, this tendency to interpret can get us into a good bit of trouble when the interpretation is wrong.
In ordinary language “some” can mean “some particular thing” or “some thing or other from a class of things” and, depending on its use, will signify completely different statements. Compare the statement “Some ice cream flavor is liked by every student” to “Every student likes some ice cream flavor.” The first statement indicates a particular flavor exists that is liked by all, while the second statement suggests that each and every student has his or her favorite.6
Take a look at Figure 17. Here we have a question taken from the ETS Tests at a Glance to introduce prospective teachers to the general knowledge examination required by many states for elementary teacher certification. This question contains examples of many of the concepts we have seen so far. For example, the sentence given is “Some values of x are less than 100” and the examinee is asked to determine which of the answers is NOT consistent with the sentence. The given sentence is a “some” proposition, and the question invokes the notion of consistency with the interference of negation.
The first choice among the answers “5 is not a value of x ” is not inconsistent with the fact that x might have some other value that is less than 100. The second choice stipulates “95 is a value of x.” Indeed, 95 could be a value of x since some of the x-values are less than 100. The third choice “Some values of x are greater than 100” could be true; it is not inconsistent with the fact that some x-values are less than 100. Many individuals will probably be tempted to choose choice D as the inconsistent answer, but not if they know that “some” means “some and possibly all.” That leaves choice E, which is in direct contradiction to the given statement. If “Some values of x are less than 100,” then it can’t be true that “No numbers less than 100 are values of x.”

Figure 17. Sample question from Tests at a Glance (ETS). (Source: The PRAXIS Series: Professional Assessments for Beginning Teachers, Mathematics (0730) Tests at a Glance at http://www.ets.org/praxis/taags/prx0730.html. Reprinted by permission of Educational Testing Service, the copyright owner.)
The four types of propositions, A, E, I, and O, were the foundation for Aristotle’s logic and all that he deemed necessary to develop his rules of logical argument. Aristotle disregarded statements with more than one quantifier—statements like: “Every critic liked some of her films” and “Some critics liked all of her films.” Matters could get even more complex if we introduce negation along with more than one quantifier. Consider the following:
Not all of the family enjoyed all of her recipes.
Some of the family did not enjoy all of her recipes.
Some of the family did not enjoy some of her recipes.
All of the family did not enjoy all of her recipes.
By distributing the quantifiers and the negations appropriately, the same basic facts can be articulated in a number of different ways. Although these statements are synonymous, some are easier to grasp than others.7
In 1846, Sir William Hamilton of Edinburgh tried to improve on Aristotle’s four types of propositions by allowing quantification of the predicate.8 In his New Analytic of Logical Forms, he distinguished eight different forms, defining “some” as “some but only some.”
1. All A is all B.
2. All A is some B.
3. Some A is all B.
4. Some A is some B.
5. Any A is not any B.
6. Any A is not some B.
7. Some A is not any B.
8. Some A is not some B.9
While this system seemed more complete than Aristotle’s, there were many difficulties associated with Hamilton’s system. His work led to a famous controversy with the English mathematician Augustus De Morgan. One point of disagreement was over Hamilton’s definition of some. Should “some” mean “some at most” or “some at least” or “some but not the rest”? De Morgan insisted that some is vague and should remain so. “Here some is a quantity entirely vague in one direction: it is not-none; one at least; or more; all, it may be. Some, in common life, often means both not-none and not-all; in logic, only not-none.”10 The American logician Charles Sanders Peirce agreed with De Morgan, saying that “some” ought to mean only “more than none.”11
Hamilton could not really improve upon Aristotle’s system; its simplicity had enabled it to remain basically unchanged for two thousand years. With only four types of propositions (A, E, I, and O), Aristotle described a structure for logical argument that could be relied upon to yield valid conclusions. His arguments became known as syllogisms. Not only would the syllogistic structure always lead to valid conclusions, but as we’ll see in Chapter 5, the system could be used to detect rhetoric that led to invalid conclusions.