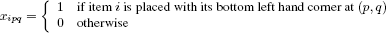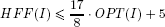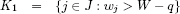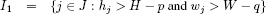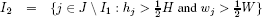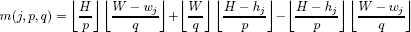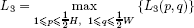Chapter 5

Two-dimensional Bin Packing Problems ¹

5.1. Introduction

In the two-dimensional bin packing problem (2BP) we are given a set of n rectangular items j ∈ J = {1,…, n}, each of width w_j and height h_j, and an unlimited number of finite identical rectangular bins, of width W and height H. The problem is to allocate, without overlapping, all the items to the minimum number of bins, with their edges parallel to those of the bins. It is assumed that the items have fixed orientation, i.e., they cannot be rotated.

An important variant of 2BP, which is also used in some approximation algorithms for its solution, is the strip packing problem (2SP), in which the items have to be packed in a strip of width W and infinite height, so as to minimize the height at which the strip is used.

Without loss of generality, we will assume throughout this work that all input data are positive integers, and that w_j W and h_j H (j = 1,…, n).

Two dimensional packing problems have many industrial applications, especially in cutting (e.g., wood, glass and paper industries) and packing (e.g., transportation, telecommunications and warehousing).

The special case where w_j = W (j = 1,…, n) is the famous one-dimensional bin packing problem (1BP): partition n elements, each having an associated size h_j, into the minimum number of subsets so that the sum of the sizes in each subset does not exceed a given capacity H. Since 1BP is known to be strongly NP-hard, the same holds for 2BP.

We survey recent advances obtained for the two-dimensional bin packing problem. With regard to heuristics, we will only consider off-line algorithms, for which it is assumed that the algorithm has full knowledge of the whole input. The reader is referred to Csirik and Woeginger [CSI 96] for a survey of on-line algorithms, which pack each item as soon as it is encountered, without knowledge of the next items.

In the next section, we start by reviewing classical mathematical models which have implications relevant to the topic of the present survey, and discuss more recent results. The following sections are devoted to upper bounds (section 5.3), including metaheuristics and approximation algorithms, lower bounds (section 5.4), and exact algorithms (section 5.5). Some worst-case results are also discussed.

Preliminary versions of parts of this work appeared in Lodi, Martello and Vigo [LOD 07] (French translation, courtesy of Elsevier, of Lodi, Martello and Vigo [LOD 02b]), and in Lodi, Martello and Monaci [LOD 02a].

5.2. Models

The first attempt to model two-dimensional packing problems was made by Gilmore and Gomory [GIL 65], through an extension of their approach to 1BP [GIL 61, GIL 63]. They proposed a column generation approach (see Lübbecke and Desrosiers [LUB 05] for a recent survey, and Soumis [SOU 97] for an annotated bibliography) based on the enumeration of all subsets of items (patterns) that can be packed into a single bin. Let A_j be a binary column vector of n elements a_ij (i = 1,…, n) taking the value 1 if item i belongs to the j-th pattern, and the value 0 otherwise. The set of all feasible patterns is then represented by the matrix A composed of all possible A_j columns (j = 1,…, M), and the corresponding mathematical model is

[5.1] 

[5.2] 

[5.3] 

where x_j takes the value 1 if pattern j belongs to the solution, and the value 0 other-wise. Observe that [5.1]–[5.3] also represent a valid model for 1BP, the only difference being that the A_js are all columns satisfying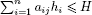

Due to the immense number of columns that can appear in A, the only way to handle the model is to dynamically generate columns when needed. While for 1BP Gilmore and Gomory [GIL 61, GIL 63] gave a dynamic programming approach for generating columns by solving, as a slave problem, an associated 0–1 knapsack problem (see Martello and Toth [MAR 90]), for 2BP they observed the inherent difficulty of the two-dimensional associated problem. Hence, they switched to the more tractable case where the items have to be packed in rows forming levels (see section 5.2.1), for which the slave problem was solved using a two-stage dynamic programming algorithm.

Beasley [BEA 85] considered a two-dimensional cutting problem in which a profit is associated with each item, and the objective is to pack a maximum profit subset of items into a single bin (two-dimensional knapsack problem). He gave an ILP formulation based on the discrete representation of the geometrical space and the use of coordinates at which items may be allocated, namely

[5.4] 

for i = 1,…, n, p = 0,…, W − w_i and q = 0,…, H − h_i. A similar model, in which p and q coordinates are handled using distinct decision variables, has been introduced by Hadjiconstantinou and Christofides [HAD 95a]. Both models are used to provide upper bounds through Lagrangian relaxation and subgradient optimization.

A completely different modeling approach has been proposed by Fekete and Schepers [FEK 04a], using a graph-theoretical characterization of the packing of a set of items into a single bin. Let G_w = (V, E_w) (resp. G_h = (V, E_h)) be an interval graph having a vertex v_i associated with each item i in the packing and an edge between two vertices (v_i, v_j) if and only if the projections of items i and j on the horizontal (resp. vertical) axis overlap (see Figure 5.1). It is proved in [FEK 04a] that if the packing is feasible then:

(a) for each stable set S of G_w (resp. G_h),;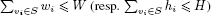

(b) E_w ∩ E_h = ∅.

This characterization can be easily extended to packings in higher dimensions.

5.2.1. ILP models for level packing

ILP models involving a polynomial number of variables and constraints have been obtained by Lodi, Martello and Vigo [LOD 04a] for the special case where the items have to be packed “by levels”.

Figure 5.1. Fekete and Schepers modeling approach

As will be seen in the next section, most of the approximation algorithms for 2BP and 2SP pack the items in rows forming levels. The first level is the bottom of the bin, and items are packed with their base on it. The next level is determined by the horizontal line drawn on the top of the tallest item packed on the level below, and so on. Note that we do not require that all items in a level have the same height. Let us denote by 2LBP problem 2BP restricted to this kind of packing.

We assume in the following, without loss of generality, that only normalized packings are considered, i.e., packings such that:

(i) in each level, the leftmost item is the tallest one;

(ii) the items are sorted and renumbered by non-increasing h_j values.

We will say that the leftmost item in a level (resp. the bottom level in a bin) initializes the level (resp. the bin).

Problem 2LBP can be efficiently modeled by assuming that there are n potential levels (the i-th one associated with item i initializing it), and n potential bins (the k-th one associated with potential level k initializing it). Hence let y_i, I ∈ J (resp. q_k, k ∈ J) be a binary variable taking the value 1 if item i initializes level i (resp. level k initializes bin k), and the value 0 otherwise. The problem can thus be modeled as

[5.5] 

[5.6] 

[5.7] 

[5.8] 

[5.9] 

[5.10] 

where x_ij, i ∈ J \ {n} and j > i (resp. z_ki, k ∈ J \ {n} and i > k), takes the value 1 if item j is packed in level i (resp. level i is allocated to bin k), and the value 0 otherwise. The restrictions j > i and i > k follow easily from assumptions (i)–(iii) above. Equations [5.6] and [5.8] impose, respectively, that each item is packed exactly once, and that each used level is allocated to exactly one bin. Equations [5.7] and [5.9] impose, respectively, the width constraint to each used level and the height constraint to each used bin.

Computational experiments have shown that the above model is quite useful in practice. Its direct use with a commercial ILP solver produces very good solutions (and, in many cases, the optimal solution) to realistically sized instances within short CPU times. In addition, several variants of the problem can be easily handled by modifying some of the constraints, or by adding linear constraints to the models.

By relaxing the integrality condition, the model produces useful lower bounds, as shown in section 5.4.1.

The set covering model [5.1]–[5.3] can be adapted to 2LBP, and to the level version of 2SP (see, for example, Bettinelli, Ceselli and Righini [BET 08]). In this case, each column corresponds to a set of items which can be inserted into a shelf, and the associated pricing problem turns out to be a simple variant of the knapsack problem.

5.3. Upper bounds

Most of the off-line heuristic algorithms from the literature are of the greedy type, and can be classified in two families:

– One-phase algorithms directly pack the items into the finite bins.

– Two-phase algorithms start by packing the items into a single strip of width W. In the second phase, the strip solution is used to construct a packing into finite W × H bins.

In addition, most of the approaches are level algorithms. Three classical strategies for the level packing have been derived from well-known algorithms for the one-dimensional case. In each case, the items are initially sorted by non-decreasing height and packed in the corresponding sequence. Let j denote the current item, and s the last created level:

– Next-fit decreasing height (NFDH) strategy: item j is packed left justified on level s, if it fits. Otherwise, a new level (s := s + 1) is created, and j is packed left justified into it.

– First-fit decreasing height (FFDH) strategy: item j is packed left justified on the first level where it fits, if any. If no level can accommodate j, a new level is initialized as in NFDH.

– Best-fit decreasing height (BFDH) strategy: item j is packed left justified on that level, among those where it fits, for which the unused horizontal space is a minimum. If no level can accommodate j, a new level is initialized as in NFDH.

Before describing two-phase algorithms, we need to briefly introduce algorithms for packing the items into a strip. In what follows we assume, unless otherwise specified, that the items are initially sorted by non-increasing height.

5.3.1. Strip packing

Coffman, Garey, Johnson and Tarjan [COF 80] analyzed NFDH and FFDH for the solution of the two-dimensional strip packing problem, in which we are required to pack all the items into a strip of minimum height, and determined their asymptotic worst-case behavior. Given a minimization problem P and an approximation algorithm A, let A(I) and OPT(I) denote the value produced by A and the optimal solution value, respectively, for an instance I of P. Coffman, Garey, Johnson and Tarjan [COF 80] proved that, if the heights are normalized so that max_j{h_j} = 1, then

[5.11]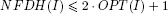 

and

[5.12]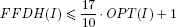 

Both bounds are tight (meaning that the multiplicative constants are as small as possible) and, if the h_js are not normalized, only the additive term is affected. Observe the similarity of [5.11] and [5.12] to the well-known results on the one-dimensional counterparts of NFDH and FFDH (algorithms Next-fit and First-fit, respectively; see Johnson, Demers, Ullman, Garey and Graham [JOH 74]).

Any algorithm requiring item sorting is obviously Ω(n log n). Both NFDH and FFDH can be implemented so as to require O(n log n) time by using the appropriate data structures adopted for the one-dimensional case (see Johnson [JOH 73]).

Several other papers on the strip packing problem can be found in the literature: see, for example, Baker, Coffman and Rivest [BAK 80], Sleator [SLE 80], Brown [BRO 80], Golan [GOL 81], Baker, Brown and Katseff [BAK 81], Baker and Schwarz [BAK 83], Høyland [HOY 88], and Steinberg [STE 97]. The Baker, Coffman and Rivest’s algorithm [BAK 80] is considered in section 5.3.4, while the other results, which have not been directly used for the finite bin case are beyond the scope of this survey and will not be discussed here.

5.3.2. Bin packing: two-phase heuristics

A two-phase algorithm for the finite bin packing problem, called hybrid first-fit (HFF), was proposed by Chung, Garey and Johnson [CHU 82]. In the first phase, a strip packing is obtained through the FFDH strategy. Let H₁, H₂,… be the heights of the resulting levels, and observe that H₁ 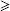H₂ 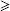…. A finite bin packing solution is then obtained by heuristically solving a one-dimensional bin packing problem (with item sizes H_i and bin capacity H) using the first-fit decreasing algorithm: initialize bin 1 to pack level 1, and, for increasing i = 2,…, pack the current level i into the lowest indexed bin where it fits, if any; if no bin can accommodate i, initialize a new bin. Chung, Garey and Johnson [CHU 82] proved that if the heights are normalized to one then

[5.13] 

The bound is not proved to be tight: the worst example gives . (OPT(I) − 1). Both phases can be implemented so as to require O(n log n) time.

Berkey and Wang [BER 87] proposed and experimentally evaluated a two-phase algorithm called finite best-strip (FBS), which is a variation of HFF. The first phase is performed using the BFDH strategy. In the second phase, the one-dimensional bin packing problem is solved using the best-fit decreasing algorithm: pack the current level in that bin, among those where it fits (if any), for which the unused vertical space is a minimum, or by initializing a new bin. (For the sake of uniformity, hybrid best-fit would be a more appropriate name for this algorithm.)

Let us now consider another variation of HFF, in which the NFDH strategy is adopted in the first phase, and the one-dimensional bin packing problem is solved using the next-fit decreasing algorithm: pack the current level in the current bin if it fits, or initialize a new (current) bin otherwise. Due to the next-fit policy, this algorithm is equivalent to a one-phase algorithm in which the current item is packed on the current level of the current bin, if possible; otherwise, a new (current) level is initialized either in the current bin (if enough vertical space is available), or in a new (current) bin. Frenk and Galambos [FRE 87] analyzed the resulting algorithm, hybrid next-fit (HNF), by characterizing its asymptotic worst-case performance as a function of max_j{w_j} and max_j{h_j}. By assuming that the heights and widths are normalized to one, the worst performance occurs for 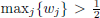and 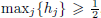, and gives:

[5.14] 

where 3.382… is an approximation for a tight but irrational bound. The three algorithms above can be implemented so as to require O(n log n) time.

The next two algorithms have higher worst-case time complexities, although they are, in practice, very fast and effective.

Lodi, Martello and Vigo [LOD 98, LOD 99b] presented an approach (floor–ceiling, FC) which extends the way items are packed on the levels. Denote the horizontal line defined by the top (resp. bottom) edge of the tallest item packed on a level as the ceiling (resp. floor) of the level. The previous algorithms pack the items from left to right with their bottom edge on the level floor. Algorithm FC may, in addition, pack them, from right to left, with their top edge on the level ceiling. The first item packed on a ceiling can only be one which cannot be packed on the floor below. A possible floor– ceiling packing is shown in Figure 5.2. In the first phase, the current item is packed, in order of preference: (i) on a ceiling (provided that the requirement above is satisfied), according to a best-fit strategy; (ii) on a floor, according to a best-fit strategy; (iii) on the floor of a new level. In the second phase, the levels are packed into finite bins, either using the best-fit decreasing algorithm or by using an exact algorithm for the one-dimensional bin packing problem, halted after a pre-fixed number of iterations.

Figure 5.2. FC algorithm

The implementation of the first phase given in [LOD 98] requires O(n³) time, while the complexity of the second one obviously depends on the selected algorithm.

Another level packing strategy based on the exact solution of induced subproblems is adopted in the knapsack packing (KP) algorithm proposed by Lodi, Martello and Vigo [LOD 99b]. The first phase of the algorithm packs one level at a time as follows. The first (tallest) unpacked item, say j^∗, initializes the level, which is then completed by solving an associated knapsack problem instance over all the unpacked items, where: (i) the knapsack capacity is W − w_j∗; (ii) the weight of an item j is w_j; (iii) the profit of an item j is its area w_j h_j. Finite bins are finally obtained as in the FC algorithm. The KP algorithm (as well as the FC algorithm) may require the solution of NP-hard subproblems, producing a non-polynomial time complexity. In practice, however, the execution of the codes for NP-hard problems is always halted after a pre-fixed (small) number of iterations, and, in almost all cases, the optimal solution is obtained before the limit is reached (see the computational experiments in [LOD 99b]).

5.3.3. Bin packing: one-phase level heuristics

Two one-phase algorithms were presented and experimentally evaluated by Berkey and Wang [BER 87].

The finite next-fit (FNF) algorithm directly packs the items into finite bins in exactly the same way as the HNF algorithm of the previous section does. (The papers [BER 87] and [FRE 87] appeared in the same year.)

The finite first-fit (FFF) algorithm adopts the FFDH strategy instead. The current item is packed on the lowest level of the first bin where it fits; if no level can accommodate it, a new level is created either in the first suitable bin, or by initializing a new bin (if no bin has enough vertical space available).

Both algorithms can be implemented so as to require O(n log n) time.

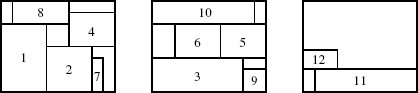
Figure 5.3. Algorithm AD

5.3.4. Bin packing: one-phase non-level heuristics

Finally, we consider algorithms which do not pack the items by levels. All the algorithms discussed in the following are one-phase.

The main non-level strategy is known as bottom-left (BL), and consists of packing the current item in the lowest possible position, left justified. Baker, Coffman and Rivest [BAK 80] analyzed the worst-case performance of the resulting algorithm for the strip packing problem, and proved that: (i) if no item ordering is used, BL may be arbitrarily bad; (ii) if the items are ordered by non-increasing width then BL(I) 3 · OPT(I), and the bound is tight.

Berkey and Wang [BER 87] proposed the BL approach for the finite bin case. Their finite bottom-left (FBL) algorithm initially sorts the items by non-increasing width. The current item is then packed in the lowest position of any initialized bin, left justified; if no bin can accommodate it, a new one is initialized. The computer implementation of the BL algorithm was studied by Chazelle [CHA 83], who gave a method for producing a packing in O(n²) time. The same approach was adopted by Berkey and Wang [BER 87].

Lodi, Martello and Vigo [LOD 99b] proposed a different non-level approach, called alternate directions (AD). The method is illustrated in Figure 5.3. The algorithm initializes L bins (L being a lower bound on the optimal solution value, see section 5.4) by packing a subset of the items, following a best-fit decreasing policy (items 1, 2, 3, 7 and 9 in Figure 5.3, where it is assumed that L = 2) on their floors. The remaining items are packed, one bin at a time, into bands, alternatively from left to right and from right to left. As soon as no item can be packed in either direction in the current bin, the next initialized bin or a new empty bin (the third one in Figure 5.3, when item 11 is considered) becomes the current one. The algorithm has O(n³) time complexity.

5.3.5. Metaheuristics

Lodi, Martello and Vigo [LOD 98, LOD 99a, LOD 99b, LOD 04b] developed effective Tabu search algorithms for 2BP and for variants of the problem involving the possibility of rotating the items by 90° or the additional constraint that the items may be obtained from the resulting patterns through guillotine cuts. We briefly describe here the unified Tabu search framework given in [LOD 99b], whose main characteristic is the adoption of a search scheme and a neighborhood which are independent of the specific packing problem to be solved. The framework can thus be used for virtually any variant of 2BP, by simply changing the specific deterministic algorithm used for evaluating the moves within the neighborhood search.

Given a current solution, the moves modify it by changing the packing of a subset S of items, trying to empty a specified target bin selected among those that currently pack a small area and a relatively large number of items. Subset S is defined so as to include one item, j, from the target bin and the current contents of k other bins, and the new packing is obtained by executing an appropriate heuristic algorithm on S.

If the move packs the items of S into k (or fewer) bins, i.e., item j has been removed from the target bin, a new item is selected, a new set S is defined accordingly, and a new move is performed. Otherwise S is changed by selecting a different set of k bins, or a different item j from the target bin.

The above framework was combined with a genetic algorithm by Iori, Martello and Monaci [IOR 03] to give a hybrid algorithm for 2SP that can be easily adapted to other packing problems in two and more dimensions.

A different metaheuristic for 2BP has been proposed by Færø, Pisinger and Zachariasen [FAE 03]. Their guided local search algorithm starts from a feasible solution, and randomly removes some bins by assigning the corresponding items to the other bins. The new solution is generally infeasible, leading to an optimization problem in which we are required to minimize an objective function that measures the pairwise overlapping area. The associated neighborhood is explored through object shifts, until a feasible solution is found.

Boschetti and Mingozzi [BOS 03a, BOS 03b] proposed new lower bounds and an effective randomized multistart heuristic for 2BP which:

(i) assigns a score to each item;

(ii) packs the items, one at a time, according to decreasing values of the corresponding scores;

(iii) updates the scores by using a specified criterion; and

(iv) iterates on (ii) and (iii) until an optimal solution is found or a maximum number of iterations has been performed.

The execution of the algorithm is repeated for a given set of different criteria used for the updating of the object scores.

Monaci and Toth [MON 06] proposed a two-phase heuristic algorithm based on [5.1]–[5.3]. In the first phase (column generation), a large set of different feasible patterns is produced using heuristic algorithms from the literature; in the second phase (column optimization) a subset of patterns is selected by heuristically solving the associated set covering instance. Parreño, Alvarez-Valdes, Oliveira and Tamarit [PAR 09] recently proposed a GRASP algorithm which uses a variable neighborhood descent structure for the improvement phase. These algorithms are currently considered the best in the literature.

5.3.6. Approximation algorithms

The long-standing question of the approximability of 2BP and 2SP has been answered in recent years. A fully polynomial-time approximation scheme for 2SP was developed by Kenyon and Rémila [KEN 00], which easily produces a 2+ ε guarantee for 2BP.

Caprara, Lodi and Monaci [CAP 02b] gave an asymptotic fully polynomial time approximation scheme (AFPTAS) for 2BP with level restrictions. Later, Caprara [CAP 02a] proposed an algorithm for the general 2BP with T_∞ + ε asymptotic worst-case guarantees, where T_∞ = 1.691… is the well-known guarantee of the harmonic algorithm for 1BP (see Lee and Lee [LEE 85]). This result was further improved by Bansal, Caprara and Sviridenko [BAN 06a], who presented a general framework for improving previous approximation algorithms and obtained asymptotic approximation guarantees arbitrarily close to 1.525… for packing with or without rotations. This is currently the best known asymptotic result. Finally, concerning inapproximability, Bansal and Sviridenko [BAN 04] proved that no asymptotic polynomial time approximation scheme (APTAS) may exist for 2BP (see also Bansal, Correa, Kenyon and Sviridenko [BAN 06b]).

All previous results concern asymptotic approximability, i.e., the approximation ratio only gets close to the stated values for instances involving a very large number of items. For the absolute approximation ratio, see the paper by Zhang [ZHA 05], in which a 3-approximation algorithm for 2BP is given. A 2-approximation algorithm was obtained by van Stee [VAN 04] for the special case where the items and bins are squares, and by Harren and van Stee [HARa] for the case in which rotation by 90° is allowed. Finally, Harren and van Stee [HARb] improved their previous results by deriving an approximation algorithm for 2BP having an absolute approximation ratio equal to 2. This is the best possible polynomial time approximation for this problem, unless .

Figure 5.4. Worst-case for the area bound

5.4. Lower bounds

Good lower bounds on the optimal solution value are important both in the implementation of exact enumerative approaches and in the empirical evaluation of approximate solutions. The simplest bound for 2BP is the area bound

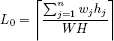
computable in linear time. Martello and Vigo [MAR 98] determined the absolute worst-case behavior of L₀:

where L₀(I) and OPT(I) denote the value produced by L₀ and the optimal solution value, respectively, for an instance I of problem P. The bound is tight, as shown by the example in Figure 5.4. The result holds even if rotation of the items (by any angle) is allowed.

A better lower bound can be obtained, in non-polynomial time, by solving the one-dimensional bin packing instance defined by element sizes w_jh_j (j = 1,…, n) and capacity WH. Caprara and Monaci [CAP 04b] showed that the optimal solution of such a 1BP instance yields a valid lower bound for 2BP, say L₁ such that for each instance I of 2BP.

In many cases, the approximation provided by both bounds can be weak, or the required computing time can be too large for effective use within an exact algorithm. A tighter bound was proposed by Martello and Vigo [MAR 98]. Given any integer value q, 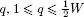, let

[5.15] 

[5.16] 

[5.17] 

and observe that no two items of K₁ ∪ K₂ may be packed side by side into a bin. Hence, a lower bound 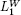for the subinstance given by the items in K₁ ∪ K₂ can be obtained by using any lower bound for the 1BP instance defined by element sizes h_j (j ∈ K₁ ∪ K₂) and capacity H (see Martello and Toth [MAR 90], Dell’Amico and Martello [DEL 95]). A lower bound for the complete instance is then obtained by taking into account the items in K₃, since none of them may be packed beside an item of K₁:

[5.18] 

A symmetric bound (q) is clearly obtained by interchanging widths and heights. By observing that both bounds are valid for any q, we have an overall lower bound:

[5.19] 

It is shown in [MAR 98] that for any instance of 2BP, the value produced by L₂ is not less than that produced by L₀, and that L₂ can be computed in O(n²) time.

Martello and Vigo [MAR 98] also proposed a computationally more expensive lower bound, which in some cases improves on L₂. Given any pair of integers (p, q), with 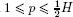and , define:

[5.20] 

[5.21] 

[5.22] 

(see Figure 5.5 (a)), and observe that: (i) I₁ ∪ I₂ is independent of (p, q); (ii) no two items of I₁ ∪ I₂ may be packed into the same bin; (iii) no item of I₃ fits into a bin containing an item of I₁. A valid lower bound can thus be computed by adding to |I₁ ∪ I₂| the minimum number of bins needed for those items of I₃ that cannot be packed into the bins used for the items of I₂. Such a bound can be determined by considering a relaxed instance where each item i ∈ I₃ has the minimum size, i.e., h_i = p and w_i = q. Given a bin containing an item j, the maximum number of p × q items that can be packed into the bin is (see Figure 5.5 (b)):

[5.23] 

Figure 5.5. (a) Items of I₁, I₂ and I₃; (b) relaxed instance with reduced items

Hence, for any pair (p, q), a valid lower bound is

[5.24] 

so an overall bound is

[5.25] 

The lower bound L₃ can be computed in O(n³) time. No dominance relation exists between L₂ and L₃.

The above bounds were further improved by Boschetti and Mingozzi [BOS 03a, BOS 03b], who also proposed some lower bounds for the 2BP variant in which items can be rotated by 90°.

Caprara, Lodi and Rizzi [CAP 04a] proposed lower bounds that exploit the compatibility relations among items represented by a graph.

Fekete and Schepers [FEK 98, FEK 04b] proposed a general bounding technique for bin and strip packing problems in one or more dimensions, based on dual feasible functions. A function u : [0, 1] → [0, 1] is called dual feasible (see Lueker [LUE 83]) if for any finite set S of non-negative real numbers, we have the relation

[5.26] 

Consider any 1BP instance, and normalize it by setting h_j = h_j/H (j = 1,…, n) and H = 1. For any dual feasible function u, any lower bound for the transformed instance having item sizes u(h₁),…, u(h_n) is then a valid lower bound for the original instance. In [FEK 98] Fekete and Schepers introduced a class of dual feasible functions for 1BP, while in [FEK 04b] they extended the approach to packing in two or more dimensions. For a d-dimensional bin packing problem, a set of d dual feasible functions {u₁,…, u_d} is called a conservative scale. Thus, given any conservative scale , a valid lower bound for 2BP is given by

[5.27] 

where the h_j and w_j values are assumed to be normalized as shown above. Given a set V of conservative scales, a valid lower bound is

[5.28] 

The approach by Fekete and Schepers was further investigated by Caprara and Monaci [CAP 09]. The basic idea is that any pair of dual feasible functions, associated with item widths and heights, respectively, leads to a valid lower bound for a given 2BP instance. The problem of determining the pair of dual feasible functions leading to the best (highest) lower bound was formulated as a disjoint bilinear program. Computational experiments in [CAP 09] showed that for most instances in the literature the resulting lower bound value is equal to that obtained by the continuous relaxation of the set covering formulation [5.1]–[5.3], while requiring computing times that are orders of magnitude smaller.

Carlier, Clautiaux and Moukrim [CAR 07a] introduced new classes of dual feasible functions that improve Fekete and Schepers’s lower bounds [FEK 04a]. Carlier and Néron [CAR 07b] considered discrete dual feasible functions, and proposed a branch-and-bound algorithm for computing all maximal discrete dual feasible functions for a given instance.

It is worth mentioning that dual feasible functions are strictly related to superadditive functions, which are commonly used to derive cuts for integer programming. The reader is referred to Clautiaux, Alves and Valerio de Carvalho [CLA 09] for a recent survey of this relationship, and a computational comparison of dual feasible functions from the literature.

5.4.1. Lower bounds for level packing

The mathematical model [5.5]–[5.10] in section 5.2.1 produces continuous bounds for 2LBP by relaxing the integrality requirements on the variables. Let L_c denote the lower bound obtained by rounding up the solution value of the resulting linear program to the closest integer. It has been proved in [LOD 04a] that this bound dominates the area bound L₀ (see section 5.4).

Lodi, Martello and Vigo [LOD 04a] also proposed a combinatorial bound that dominates the corresponding continuous bound by allowing item splitting:

(i) any item is allowed to be split into two slices of integer width through a vertical cut; and

(ii) any level is allowed to be split into two sectors of integer height through a horizontal cut.

It is shown in [LOD 04a] that such a relaxation can be solved exactly in O(n log n) time. Let L_cut denote the resulting bound. It is proved in [LOD 04a] that, for any instance I of 2LBP, 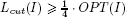, and that the worst-case bound is tight.

5.5. Exact algorithms

An enumerative approach for the exact solution of 2BP has been presented by Martello and Vigo [MAR 98]. The items are initially sorted in non-increasing order of their area. A reduction procedure tries to determine the optimal packing of some bins, thus reducing the size of the instance. A first solution, of value z^∗, is then heuristically obtained.

The algorithm is based on a two-level branching scheme:

– outer branch decision tree: at each decision node, an item is assigned to a bin without specifying its actual position;

– inner branch decision tree: a feasible packing (if any) for the items currently assigned to a bin is determined, possibly through enumeration of all the possible patterns.

The outer branch decision tree is searched in a depth-first way, making use of the lower bounds described in the previous section. Whenever it is possible to establish that no more unassigned items can be assigned to a given initialized bin, such a bin is closed: an initialized and not closed bin is called active. At level k (k = 1,…, n), item k is assigned, in turn, to all the active bins and, possibly, to a new one (if the total number of active and closed bins is less than z^∗ − 1).

The feasibility of the assignment of an item to a bin is first heuristically checked. A lower bound L(I) is computed for the instance I defined by the items currently assigned to the bin: if L(I) > 1, a backtracking follows. Otherwise, heuristic algorithms are applied to I: if a feasible single-bin packing is found, the outer enumeration is resumed. If not, the inner branching scheme enumerates all the possible ways to pack I into a bin through the left-most downward strategy (see Hadjiconstantinou and Christofides [HAD 95b]): at each level, the next item is placed, in turn, into all positions where it has its left edge adjacent either to the right edge of another item or to the left edge of the bin, and its bottom edge adjacent either to the top edge of another item or to the bottom edge of the bin. As soon as a feasible packing is found for all the items of I, the outer enumeration is resumed. If no such packing exists, an outer backtracking is performed.

Whenever the current assignment is feasible, the possibility of closing the bin is checked through lower bound computations.

Martello, Monaci and Vigo [MAR 03] presented a branch-and-bound algorithm for the two-dimensional strip packing problem, in which lower bounds are computed through a relaxation that replaces each w_j × h_j item with h_j unit-height one-dimensional items of width w_j, thus inducing an instance of 1BP.

Fekete, Schepers and van der Veen [FEK 07] developed an enumerative approach to the exact solution of the problem of packing a set of items into a single bin. Such an approach is based on the model presented in [FEK 04a] and is discussed in section 5.2, and could be used for alternative exact approaches to 2BP and 2SP. Specifically,

(i) for 2BP, it could be used in place of the inner decision-tree of the two-level approach above;

(ii) for 2SP, we could determine, by a binary search, the minimum height such that all the items can be packed into a single bin of base W and height .

More recently, Pisinger and Sigurd [PIS 07] implemented a branch-and-price algorithm for the exact solution of [5.1]–[5.3]. As mentioned in section 5.2, the slave problem in column generation requires determination of a suitable set of items to be packed into a single bin. This is solved in [PIS 07] as a constraint-satisfaction problem, using forward propagation to prune dominated arrangements of rectangles.

5.6. Acknowledgments

We thank the Ministero dell’Istruzione, dell’Università e della Ricerca (MIUR), Italy, for the support given to this project.

5.7. Bibliography

[BAK 80] B.S. BAKER, E.G. COFFMAN, JR. and R.L. RIVEST. “Orthogonal packing in two dimensions”, SIAM Journal on Computing, 9:846–855, 1980.

[BAK 81] B.S. BAKER, D.J. BROWN and H.P. KATSEFF. “A 5/4 algorithm for two-dimensional packing”, Journal of Algorithms, 2:348–368, 1981.

[BAK 83] B.S. BAKER and J.S. SCHWARZ. “Shelf algorithms for two-dimensional packing problems”, SIAM Journal on Computing, 12:508–525, 1983.

[BAN 04] N. BANSAL and M. SVIRIDENKO. “New approximability and inapproximability results for 2-dimensional bin packing”, In Proceedings of the 15th ACM-SIAM Symposium on Discrete Algorithms (SODA 2004), pages 189–196, 2004.

[BAN 06a] N. BANSAL, A. CAPRARA and M. SVIRIDENKO. “Improved approximation algorithms for multidimensional bin packing problems”, In Proceedings of 47nd IEEE Symposium on Foundations of Computer Science (FOCS 2006), pages 697–708, 2006.

[BAN 06b] N. BANSAL, J.R. CORREA, C. KENYON and M. SVIRIDENKO. “Bin packing in multiple dimensions: inapproximability results and approximation schemes”, Mathematics of Operations Research, 31:31–49, 2006.

[BEA 85] J.E. BEASLEY. “An exact two-dimensional non-guillotine cutting tree search procedure”, Operations Research, 33:49–64, 1985.

[BER 87] J.O. BERKEY and P.Y. WANG. “Two dimensional finite bin packing algorithms”, Journal of the Operational Research Society, 38:423–429, 1987.

[BET 08] A. BETTINELLI, A. CESELLI and G. RIGHINI. “A branch-and-price algorithm for the two-dimensional level strip packing problem”, 4OR, 6: 361–374, 2008.

[BOS 03a] M.A. BOSCHETTI and A. MINGOZZI. “The two-dimensional finite bin packing problem. Part I: New lower bounds for the oriented case”, 4OR, 1:27–42, 2003.

[BOS 03b] M.A. BOSCHETTI and A. MINGOZZI. “The two-dimensional finite bin packing problem. Part II: New lower and upper bounds”, 4OR, 2:135–148, 2003.

[BRO 80] D.J. BROWN. “An improved BL lower bound”, Information Processing Letters, 11:37–39, 1980.

[CAP 02a] A. CAPRARA. “Packing 2-dimensional bins in harmony”, In Proceedings of the 43-rd Annual IEEE Symposium on Foundations of Computer Science (FOCS 2002). IEEE Computer Society Press, 2002.

[CAP 02b] A. CAPRARA, A. LODI and M. MONACI. “Fast approximation schemes for two-stage, two-dimensional bin packing”, Mathematics of Operations Research, 30:150–172, 2005.

[CAP 04a] A. CAPRARA, A. LODI and R. RIZZI. “On d-threshold graphs and d-dimensional bin packing”, Networks, 44:266–280, 2004.

[CAP 04b] A. CAPRARA and M. MONACI. “On the two-dimensional knapsack problem”, Operations Research Letters, 32:5–14, 2004.

[CAP 09] A. CAPRARA and M. MONACI. “Bidimensional packing by bilinear programming”, Mathematical Programming, 118:75–108, 2009.

[CAR 07a] J. CARLIER, F. CLAUTIAUX and A. MOUKRIM. “New reduction procedures and lower bounds for the two-dimensional bin packing with fixed orientation”, Computers & Operations Research, 34:2233–2250, 2007.

[CAR 07b] J. CARLIER and E. NÉRON. “Computing redundant resources for the resource constrained project scheduling problem”, European Journal of Operational Research, 176:1452–1463, 2007.

[CHA 83] B. CHAZELLE “The bottom-left bin packing heuristic: An efficient implementation”, IEEE Transactions on Computers, 32:697–707, 1983.

[CHU 82] F.K.R. CHUNG, M.R. GAREY and D.S. JOHNSON. “On packing two-dimensional bins”, SIAM Journal of Algebraic and Discrete Methods, 3:66–76, 1982.

[CLA 09] F. CLAUTIAUX, C. ALVES and J.M. VALÉRIO DE CARVALHO. “A survey of dual-feasible and superadditive functions”, Annals of Operations Research, 2009.

[COF 80] E.G. COFFMAN, JR., M.R. GAREY, D.S. JOHNSON and R.E. TARJAN. “Performance bounds for level-oriented two-dimensional packing algorithms”, SIAM Journal on Computing, 9:801–826, 1980.

[CSI 96] J. CSIRIK and G. WOEGINGER. “On-line packing and covering problems”, In Online Algorithms, volume 1442, pages 147–177. Springer Lecture Notes in Computer Science, 1996.

[DEL 95] M. DELL’AMICO and S.MARTELLO. “Optimal scheduling of tasks on identical parallel processors”, ORSA Journal on Computing, 7:191–200, 1995.

[FAE 03] O. FÆRØ, D. PISINGER and M. ZACHARIASEN. “Guided local search for the three-dimensional bin packing problem”, INFORMS Journal on Computing, 15:267–283, 2003.

[FEK 98] S.P. FEKETE and J. SCHEPERS. “New classes of lower bounds for bin packing problems”, In Integer Programming and Combinatorial Optimization (IPCO 98), volume 1412, pages 257–270. Springer Lecture Notes in Computer Science, 1998.

[FEK 04a] S.P. FEKETE and J. SCHEPERS. “A combinatorial characterization of higher-dimensional orthogonal packing”, Mathematics of Operations Research, 29:353–368, 2004.

[FEK 04b] S.P. FEKETE and J. SCHEPERS. “A general framework for bounds for higher-dimensional orthogonal packing problems”, Mathematical Methods of Operations Research, 60:311–329, 2004.

[FEK 07] S.P. FEKETE, J. SCHEPERS and J. VAN DER VEEN. “An exact algorithm for higher-dimensional orthogonal packing”, Operations Research, 55:569–587, 2007.

[FRE 87] J.B. FRENK and G.G. GALAMBOS. “Hybrid next-fit algorithm for the two-dimensional rectangle bin-packing problem”, Computing, 39:201–217, 1987.

[GIL 61] P.C. GILMORE and R.E. GOMORY. “A linear programming approach to the cutting stock problem”, Operations Research, 9:849–859, 1961.

[GIL 63] P.C. GILMORE and R.E. GOMORY. “A linear programming approach to the cutting stock problem – part II”, Operations Research, 11:863–888, 1963.

[GIL 65] P.C. GILMORE and R.E. GOMORY. “Multistage cutting problems of two and more dimensions”, Operations Research, 13:94–119, 1965.

[GOL 81] I. GOLAN. “Performance bounds for orthogonal oriented two-dimensional packing algorithms”, SIAM Journal on Computing, 10:571–582, 1981.

[HAD 95a] E. HADJICONSTANTINOU and N. CHRISTOFIDES. “An exact algorithm for the orthogonal, 2-D cutting problems using guillotine cuts”, European Journal of Operational Research, 83:21–38, 1995.

[HAD 95b] E. HADJICONSTANTINOU and N. CHRISTOFIDES. “An exact algorithm for general, orthogonal, two-dimensional knapsack problems”, European Journal of Operational Research, 83:39–56, 1995.

[HARa] R. HARREN and R. VAN STEE. “Absolute approximation ratios for packing rectangles into bins”, Journal of Scheduling, forthcoming.

[HARb] R. HARREN and R. VAN STEE. “An absolute 2-approximation algorithm for two-dimensional bin packing”, Submitted for publication. Available on the Internet at http://www.mpi-inf.mpg.de/∼rharren/.

[HOY 88] S. HØYLAND. “Bin-packing in 1.5 dimension”, In Proc. Scandinavian Workshop on Algorithm Theory, volume 318, pages 129–137. Springer Lecture Notes in Computer Science, 1988.

[IOR 03] M. IORI, S. MARTELLO and M. MONACI. “Metaheuristic algorithms for the strip packing problem”, In P.M. Pardalos and V. Korotkikh, editors, Optimization and Industry: New Frontiers, pages 159–179, Kluwer Academic Publishers, Boston, MA, 2003.

[JOH 73] D.S. JOHNSON. Near-Optimal Bin Packing Algorithms. PhD thesis, MIT, Cambridge, MA, 1973.

[JOH 74] D.S. JOHNSON, A. DEMERS, J.D. ULLMAN, M.R. GAREY and R.L. GRAHAM. “Worst-case performance bounds for simple one-dimensional packing algorithms”, SIAM Journal on Computing, 3:299–325, 1974.

[KEN 00] C. KENYON and E. RÉMILA. “A near-optimal solution to a two-dimensional cutting stock problem”, Mathematics of Operations Research, 25:645–656, 2000.

[LEE 85] C.C. LEE and D.T. LEE. “A simple on-line bin packing algorithm”, Journal of the ACM, 32:562–572, 1985.

[LOD 98] A. LODI, S. MARTELLO and D. VIGO. “Neighborhood search algorithm for the guillotine non-oriented two-dimensional bin packing problem”, In S. Voss, S. Martello, I.H. Osman, and C. Roucairol, editors, Meta-Heuristics: Advances and Trends in Local Search Paradigms for Optimization, pages 125–139. Kluwer Academic Publishers, Boston, 1998.

[LOD 99a] A. LODI, S. MARTELLO and D. VIGO. “Approximation algorithms for the oriented two-dimensional bin packing problem”, European Journal of Operational Research, 112:158–166, 1999.

[LOD 99b] A. LODI, S. MARTELLO and D. VIGO. “Heuristic and metaheuristic approaches for a class of two-dimensional bin packing problems”, INFORMS Journal on Computing, 11:345–357, 1999.

[LOD 02a] A. LODI, S. MARTELLO and M. MONACI. “Two-dimensional packing problems: A survey”, European Journal of Operational Research, 141:3–13, 2002.

[LOD 02b] A. LODI, S. MARTELLO and D. VIGO. “Recent advances on two-dimensional bin packing problems”, Discrete Applied Mathematics, 123:379–396, 2002.

[LOD 04a] A. LODI, S. MARTELLO and D. VIGO. “Models and bounds for two-dimensional level packing problems”, Journal of Combinatorial Optimization, 8:363–379, 2004.

[LOD 04b] A. LODI, S. MARTELLO and D. VIGO. “TSpack: A unified tabu search code for multi-dimensional bin packing problems”, Annals of Operations Research, 131:203–213, 2004.

[LOD 07] A. LODI, S. MARTELLO and D. VIGO. “Récentes avancées sur le problème de bin packing à deux dimensions”, In Optimisation Combinatoire 4: Problèmes Paradigmatiques, pages 137–161. Hermes Science Publications, Paris, 2007.

[LUB 05] M. LÜBBECKE and J. DESROSIERS. “Selected topics in column generation”, Operations Research, 53:1007–1023, 2005.

[LUE 83] G.S. LUEKER. “Bin packing with items uniformly distributed over intervals [a,b]”, In Proc. 24th Annual Symp. Found. Comp. Sci., pages 289–297, 1983.

[MAR 90] S. MARTELLO and P. TOTH. Knapsack Problems: Algorithms and Computer Implementations. John Wiley & Sons, Chichester, 1990.

[MAR 98] S. MARTELLO and D. VIGO. “Exact solution of the two-dimensional finite bin packing problem”, Management Science, 44:388–399, 1998.

[MAR 03] S. MARTELLO, M. MONACI and D. VIGO. “An exact approach to the strip packing problem”, INFORMS Journal on Computing, 15:310–319, 2003.

[MON 06] M. MONACI and P. TOTH. “A set-covering based heuristic approach for bin-packing problems”. INFORMS Journal on Computing, 18:71–85, 2006.

[PAR 09] E. PARREÑO, R. ALVAREZ-VALDES, J.F. OLIVEIRA and J.M. TAMARIT. “A hybrid GRASP/VND algorithm for two- and three-dimensional bin packing”, Forthcoming on Annals of Operations Research, 2009.

[PIS 07] D. PISINGER and M.M. SIGURD. “Using decomposition techniques and constraint programming for solving the two-dimensional bin packing problem”, INFORMS Journal on Computing, 19:36–51, 2007.

[SLE 80] D. SLEATOR. “A 2.5 times optimal algorithm for packing in two dimensions”, Information Processing Letters, 10:37–40, 1980.

[SOU 97] F. SOUMIS. “Decomposition and column generation”, In M. Dell’Amico, F. Maffioli and S. Martello (eds.), Annotated Bibliographies in Combinatorial Optimization. John Wiley & Sons, Chichester-New York, 115–126, 1997.

[STE 97] A. STEINBERG. “A strip-packing algorithm with absolute performance bound 2”, SIAM Journal on Computing, 26:401–409, 1997.

[VAN 04] R. VAN STEE. “An approximation algorithm for square packing”, Operations Research Letters, 32:535–539, 2004.

[ZHA 05] G. ZHANG. “A 3-approximation algorithm for two-dimensional bin packing”, Operations Research Letters, 33:121–126, 2005.

---

1 Chapter written by Andrea LODI, Silvano MARTELLO, Michele MONACI and Daniele VIGO.