chapter two

Flow traffic models

2.1  Background in traffic modeling

2.1.1  Definition of the informational traffic

One important research area in the context of networking focuses on developing traffic models that can be applied to the Internet and, more generally, to any communication network. The interest in such models is twofold. First, traffic models are needed as an input in network simulations. In turn, these simulations must be performed in order to study and validate algorithms and protocols that can be applied to real traffic, and to analyze how traffic responds to particular network conditions (e.g., congestion). Thus, it is essential that the proposed models reflect as much as possible the relevant characteristics of the traffic it is supposed to represent. Second, a good traffic model may lead to a better understanding of the characteristics of the network traffic itself. This, in turn, can prove to be useful in designing routers and devices which handle network traffic.

A traffic model represents a stochastic process, which can be used also to predict the behavior of a real traffic stream. Ideally, the traffic model should accurately represent all of the relevant statistical properties of the original traffic, but such a model may become overly complex. A major application of traffic models is the prediction of the behavior of the traffic as it passes through a network. In this context, the response of the individual network elements in the traditional Internet can be modeled using one or more single server queues (SSQs). Hence, a useful model for network traffic modeling applications is the one that accurately predicts queuing performance in an SSQ. Matching the first- and second-order statistics provides us with confidence that such a performance matching is not just a lucky coincidence. In order to keep our modeling parsimonious, we aim to typify a given traffic stream using as few parameters as possible.

Usually the traffic is considered as a sequence of arrivals of discrete entities (packets, cells, etc.). Mathematically, it is a point process, which resides in a set of arrival moments $T_1,T_2,\dots ,T_n,\dots$ measured from the origin 0, that is, T₀ = 0. There are other two possible descriptions of the point processes: counting processes and interarrival time processes. A counting process ${\left\{N(t)\right\}}_{t=0}^{\infty }$ is a continuous-time, integer-valued stochastic process, where $N(t)=\max \left\{n:T_n\le t\right\}$ expresses the number of arrivals in the time interval (0,t]. An interarrival time process is a nonnegative random sequence ${\left\{A_n\right\}}_{n=1}^{\infty }$, where $A_n=T_n-T_{n-1}$ indicates the length of the interval separating arrivals n − 1 and n. The two kinds of processes are related through the following equation:

$\left\{N\left(t\right)=n\right\}=\left\{T_n\le t<T_{n+1}\right\}=\left\{{\displaystyle \sum _{k=1}^n{A}_k\le t<}{\displaystyle \sum _{k=1}^{n+1}{A}_k}\right\}$

(2.1)

The equivalence resides in the cumulative effect $T_n={\displaystyle {\sum }_{k=1}^n{A}_k}$ and in the equality of the events, supposing that the intervals between two arrivals {A_n}, form a stationary sequence. An alternate characterization of the point processes based on the theory of the stochastic intensity is presented later in Section 2.7.

In case of compound traffic, arrivals may happen in batches, that is, several arrivals can happen at the same instant T_n. This fact can be modeled by using an additional nonnegative random sequence of real values ${\left\{B_n\right\}}_{n=1}^{\infty }$, where B_n is the cardinality of the nth batch (it may be a random number). The traffic model is largely defined by the nature of the stochastic processes {N(t)} and {A_n} chosen, with the condition that the random variables A_n can have only integer values, that is, the random variables N(t) can grow only when T_n are integers.

One important issue in the selection of the stochastic process is its ability to describe traffic burstiness. In particular, a sequence of arrival times will be bursty if the T_n tend to form clusters, that is, if the corresponding {A_n} becomes a mix of relatively long and short interarrival times. Mathematically speaking, traffic burstiness is related to short-terms autocorrelations between the interarrival times. However, there is no single widely accepted notion of burstiness (Frost and Melamed 1994); instead, several different measures are used, some of which ignore the effect of second-order properties of the traffic. A first measure is the ratio of peak rate to mean rate, which though has the drawback of being dependent upon the interval used to measure the rate. A second measure is the coefficient of variation $c_A=\text{σ}[A_n]/E[A_n]$ of the interarrival times. A metric considering second-order properties of the traffic is the index of dispersion for counts (IDC). In particular, given an interval of time τ, IDC(τ) = Var[N(τ)]/E[N(τ)]. Finally, as will be better detailed later, the Hurst parameter can be used as a measure of burstiness in case of self-similar traffic.

Another useful notion is the workload process ${\left\{W_n\right\}}_{n=1}^{\infty }$. It is described by the amount of work W_n brought to the system by the nth arrival, assuming that it is independent of the interarrival times and the dimension of the groups. An example is the sequence of the requests for service times of the arrivals in a queue. In such cases, if the traffic is deterministic, only the description of the workload is necessary.

The following notation will be used: the distribution function of A_n is denoted by F_A(x). Similarly, λ_A = 1/E[A_n] denotes the traffic rate, $\begin{array}{ccc}{\text{σ}}_A^2=\text{Var[}{A}_n]& \text{and}& c_A={\text{λ}}_A{\text{σ}}_A\end{array}$ assuming also that 0 < σ_A < ∞, and that {A_n} is a simple one, that is, P{A_n = 0} = 0. A traffic flow is denoted by X when other particular description (by A, N, or T) is not necessary.

2.1.2  Internet teletraffic modeling

2.1.2.1  Introduction in teletraffic theory

Teletraffic theory (Akimaru and Kawashima 1999) is the basis for performance evolution and dimensioning of telecommunication networks. It was developed alongside the momentous changes of switching and networking technology in the last decades. The theory has incorporated the recent advances in operation research and queuing theory. Teletraffic theory deals with the application of mathematical modeling of the traffic demand, network capacity and realized performance relationships. The traffic demand is statistical in nature, resulting in the generation of relevant models derived from the theory of stochastic processes. The nature of traffic in today’s data networks (e.g., Internet) is completely different from classical telephone traffic and the main difference can be explained by the fact that in traditional telephony the traffic is highly static in nature. The static nature of telephone traffic resulted in “universal laws” governing telephone networks like the Poisson nature of call arrivals. This law states that call arrivals are mutually independent and exponentially distributed with the same parameter. The great success of the Poissonian model is due to the parsimonious modeling, which is a highly desirable property in practice.

A similar “universal law” is that the call holding times follow more or less an exponential distribution. This model was also preferred due to its simplicity and analytical tractability in spite of the fact that the actual telephone call duration distribution sometimes deviates significantly from the exponential distribution. However, these deviations did not yield to major errors in the network design due to the nature of the Poisson arrival process. This is because several performance measures do not depend on the distribution but only on the average holding time.

A dramatic change happened concerning the validity of these laws when telephone networks were used not only for voice conversations but also for FAX transmissions and Internet access. The statistical characteristics of these services are significantly different from voice calls. As the popularity of the Internet increased due to the success of Web, more people started to use the classical telephone networks for Internet access. These changes call for reviewing the old laws and present a challenge for all teletraffic researchers.

The picture is completely different in case of data networks. All the expectations of finding similar universal laws for data traffic failed. It is because data traffic is much more variable than voice traffic. Roughly speaking, it is impossible to find a general model because the individual connections of data communication can change from extremely short to extremely long and the data rate can also span a huge range. There is no static and homogenous nature of data traffic as it was found in case of the voice traffic. This extremely bursty nature of data traffic is mainly caused by the fact that this traffic is generated by machine-to-machine communication in contrast to the human-to-human communication.

This high variability of data traffic in both time (traffic dependencies do not decay exponentially fast as it was the case in voice traffic but long-term dependencies are present, e.g., in the autocorrelation of the traffic) and space (distributions of traffic-related quantities do not have exponential tails as it was the case of voice traffic) call for new models and techniques to be developed. Statistically, the long-term dependencies can be captured by long-range dependence (LRD), that is, autocorrelations that exhibit power-law decay. The extreme spatial variability can be described by heavy-tailed distributions with infinite variance, which is typically expressed by the Pareto distributions. The power-law behavior in both time and space of some statistical descriptors often cause the corresponding traffic process to exhibit fractal characteristics. The fractal properties often manifest themselves in self-similarity. It means that several statistical characteristics of the traffic are the same over a range of timescales. Self-similar traffic models seem to be successful parsimonious models to capture this complex fractal nature of network traffic in the previous decade. However, recent research indicates that the actual data traffic has a more refined burstiness structure, which is better captured by multifractality rather than only self-similarity, which is a special case of mono-fractality.

Besides the very variable characteristics of data traffic there are other factors that make predictions about data traffic characteristics more unreliable. The Internet traffic is doubling each year. The picture is even more complicated if we think of quality of service (QoS) requirements of data services which can be very different from one application to the other. Different QoS requirements generate different traffic characteristics. To describe these different traffic characteristics in case of both stream and elastic traffic flows a number of traffic models and traffic characterization techniques have been developed. Based on a successful traffic modeling, successful traffic dimensioning methods for resource allocation can also be developed.

2.1.2.2  Basic concepts of teletraffic theory

A demand for a connection in a network is defined as a call, which is activated by a customer. The call duration is defined as holding time or service time. The traffic load is the total holding time per unit time. The unit of traffic load is called erlang (erl) after the Danish mathematician Agner Krarup Erlang (1878–1929), also known as the father of teletraffic theory. The traffic load has the following important properties:

1.  The traffic load (offered traffic) a is given by a = ch (erl) where c is the number of calls originating per unit time and h is the mean holding time.

2.  The traffic load (offered traffic) is equal to the number of calls originating in the mean holding time.

3.  The traffic load (carried traffic) carried by a single trunk is equivalent to the probability (fraction of time) that the trunk is used (busy).

4.  The traffic load (carried traffic) carried by a group of trunks is equivalent to the mean (expected) number of busy trunks in the group.

A switching system is defined as a system connecting between inlets and outlets. A system is called a full availability system if any inlet can be connected to any idle outlet. Congestion is a state of the system when a connection cannot be made because of busy outlets or internal paths. The system is called a waiting or delay system if an incoming call can wait for a connection in case of congestion. If no waiting is possible in congestion state the call is blocked and the system is called as loss system or nondelay system. A full availability system can be described by the following:

1.  Input process: This describes the way of call arrival process.

2.  Service mechanism: This describes the number of outlets, service time distributions, etc.

3.  Queue discipline: This specifies ways of call handling during congestion. In delay systems the most typical queuing disciplines are the first-in first-out (FIFO), last-in first-out (LIFO), priority systems, processor sharing, etc.

The Kendall notation A/B/C/D/E-F is used for classification of full availability systems where A represents the interarrival time distribution, B the service time distribution, C the number of parallel servers, D the system capacity, E the finite customer population, and F is the queuing discipline. The following notations are used: M, exponential (Markov); E_k, phase k Erlangian; H_n, order n hyperexponential; D, deterministic; G, general; GI, general independent; MMPP, Markov-modulated Poisson process; MAP, Markov arrival process.

For a Poisson arrival process (exponential interarrival times) in steady state the distribution of existing calls at an arbitrary instant is equal to the distribution of calls just prior to call arrival epochs. This relationship is called Poisson Arrivals See Time Averages (PASTA) because this probability is equal to the average time fraction of calls existing when observed over a sufficiently long period.

If the interarrival time is exponentially distributed, the residual time seen at an arbitrary time instant is also exponential with the same parameter. A model in which the interarrival time and the service time both exponentially distributed is called the Markovian model, otherwise it is called non-Markovian model.

2.1.2.3  Teletraffic techniques

Beyond the classical queuing methods there are numerous approximations, bounds, techniques to handle teletraffic systems.

The fluid flow approximation is a useful technique when we have lots of traffic units (packets) in the timescale under investigation. In this case, we can treat it as a continuous flow-like fluid entering a piping system. We can define A(t) and D(t) to be the random variables describing the number of arrivals and departures, respectively, in (0,t). The number of customers in the system at time t is N(t) = A(t) – D(t), assuming that the system is empty initially. By the weak law of large numbers, when A(t) gets large it gets close to its mean and this is the same for D(t). The fluid flow approximation simply replaces A(t) and D(t) by the their means, which are continuous deterministic processes.

The fluid flow approximation uses mean values and the variability in the arrival and departure processes is not taken into account. The diffusion approximation extends this model by modeling this variability (motivated by the central limit theorem) by normal distribution around the mean. Diffusion approximations are also applied to solve difficult queuing systems. For example, in the complex G/G/1 system the queue length distribution can be obtained by diffusion methods.

An approach based on the information theory called the maximum entropy method is often useful in solving teletraffic systems. The basis for this method is Bernoulli’s principle of insufficient reasons which states that all events over a sample space should have the same probability unless there is evidence to the contrary. The entropy of a random variable is minimum (zero) when its value is certain. The entropy is maximum when its value is uniformly distributed because the outcome of an event has maximum uncertainty. The idea is that the entropy be maximized subject to any additional evidence. The method is successfully used for example in the queuing theory.

A number of other methods have also been developed like queuing networks with several solving techniques, fixed point methods, decomposition techniques, etc.

2.1.3  Internet teletraffic engineering

Currently network provisioning is based on some rules of the thumb and teletraffic theory has no major impact on the design of the Internet. The nature of the data traffic is significantly different from the nature of voice traffic. New techniques and models were developed in teletraffic theory of the Internet to respond to these challenges. In the following, we review the most possible two alternatives of Internet teletraffic engineering. The first is called the big bandwidth philosophy and the other is called managed bandwidth philosophy (Molnar and Miklos 1997).

2.1.3.1  Big bandwidth philosophy

There is a certain belief that there is no real need for some advanced teletraffic engineering in the Internet because the overprovisioning of resources can solve the problems. This is the big bandwidth philosophy. People from this school say that in spite of the dramatic increase in the Internet traffic volume each year, the capacity of links and also the switching and routing devices will be so cheap that overprovisioning of resources will be possible. It is worth investigating a little bit more deeply how realistic the “big bandwidth philosophy” is. It is assumed that the transmission and information technology can follow the trend of “Internet traffic doubling each year” trend and can provide cheap solutions. From a technological point of view it seems that this expectation is not unrealistic at least in the near future. Indeed, if you imagine today’s Internet and you just increase the capacity of links you could have a network that supports even real-time communications without any QoS architectures. On the other hand, the locality of data in the future will also be dominant, which makes caching an important technical issue in future networks. Even today if you want to transmit all the bits that are stored on hard drives it would take over 20 years for completing the process. This trend probably gives a relative decrease in the total volume of transmitted information.

Another important factor is that the streaming traffic, which really requires some QoS support, is not dominant in the Internet. It was believed that it would become dominant but none of these expectations have been fulfilled so far, which can also be predicted for the future. The demand for this traffic type is not growing as fast as the capacity is increasing. Consider the following example: we have 1% streaming traffic so it needs some QoS support. We have two options. We can introduce some QoS architecture or we can increase the capacity by 5%. Advocates of the “big bandwidth philosophy” school argue that the second option is cheaper. They also say that multimedia applications will use store-and-reply technique instead of real-time streaming. They argue that the capacity of storage is increasing at about the same rate as transmission capacity. Moreover, due to transmission bottlenecks (e.g., wireless link) it makes sense to store information in local.

It is also interesting if we investigate the reason for capacity increase in the previous years. For example, we can see that people are not paying for cable modems or ADSL not because their modem links could not bring them more data, but because when they click on a hyperlink they want that page on their screen immediately. So they need the big capacity, not for downloading lots of bits, but rather for achieving a low latency when they initiate a file download. This is also the reason for the fact that the average utilization of LANs have been decreased by about a factor of 10 over the last decade: people want high bandwidth to provide low latency.

Will overprovisioning be the solution? Nobody knows at this time. It is rather difficult to predict what will happen mainly because this is not only a technical issue but rather depends on political and economic factors. However, as a modest prediction we might say that even if overprovisioning can be a solution for backbone networks it is less likely that it will happen also in access networks. For cases where overprovisioning cannot be applied we have a limited capacity which should be managed somehow. This leads us to the second alternative which is the “managed bandwidth philosophy.”

2.1.3.2  Managed bandwidth philosophy

In the case of limited network resources some kind of traffic control should be implemented to provide appropriate capacity and router memory for each traffic class or stream to fulfill its QoS requirements. Basically, there are three major groups of QoS requirements: transparency, accessibility, and throughput. Transparency expresses the time and semantic integrity of the transferred data. As an example for data transfer semantic integrity is usually required but delay is not so important. Accessibility measures the probability of refusal of admission and also the delay of setup in case of blocking. As an example the blocking probability is in this class, which is a well-known and frequently used measure in telephone networks. The throughput is the main QoS measure in data networks. As an example a throughput of 100 kbit/s can ensure the transfer of most of the Web pages quasi-instantaneously (<1 s).

Considering the traffic types by nature two main groups can be identified: stream traffic and elastic traffic. The stream traffic is composed of flows characterized by their intrinsic duration and rate. Typical examples of stream traffic are the audio and video real-time applications: telephone, interactive video services, and videoconferencing. The time integrity of stream traffic must be preserved. The negligible loss, delay and jitter are the generally required QoS measures. The elastic traffic usually consists of digital objects (documents) transferred from one place to another. The traffic is elastic because the flow rate can vary due to external causes (e.g., free capacity). Typical elastic applications are the Web, e-mail, or file transfers. In case of elastic traffic the semantic integrity must be preserved. Elastic traffic can be characterized by the arrival process of requests and the distribution of object sizes. The throughput and the response time are the typical QoS measures in this class.

2.1.3.3  Open-loop control of stream traffic

The stream traffic is usually controlled by an open-loop preventive traffic control based on the notion of traffic contract. Traffic contract is a successful negotiation between the user and the network in which the user requests are described by a set of traffic parameters and required QoS parameters. Based on these requests the network performs an admission control accepting the communication and the traffic contract only if QoS requirements can be satisfied. The effectiveness of this control highly depends on how accurately the performance can be predicted based on the traffic descriptors. In practice, it turned out that it is not simple to define practically useful traffic descriptors. It is because it should be simple (understandable by the user), useful (for resource allocation), and controllable (verifiable by the network). The results of intensive research on finding such traffic descriptors with all these properties showed that it is practically impossible. As an example the standardized token bucket-type descriptors (both in ATM and Internet research bodies) are good controllable descriptors but they are less useful for resource allocation. The users are encouraged to use mechanisms (e.g., traffic shaping) to ensure declared traffic descriptors. Mechanisms can also be implemented at the network ingress to police traffic descriptors (traffic policing). Both shaping and policing are frequently based on the mentioned token bucket-type mechanisms.

The major types of open-loop traffic control (admission control) strategies depend on whether statistical multiplexing gain is aimed to be utilized and to what extent. Table 2.1 shows the main categories.

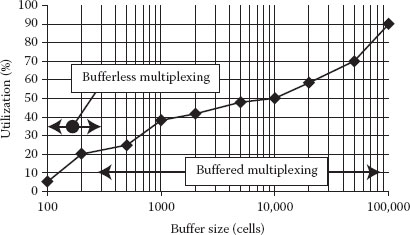
If no multiplexing gain is targeted to be achieved, we have the simplest case and we can simply allocate the maximal rate (peak rate) of all the connections, which is called the peak rate allocation. The advantage of this approach is that the only traffic descriptor is the peak rate of the connection. The admission control is very simple: it only has to check whether the sum of the required peak rates is over the total capacity. The main disadvantage of peak rate allocation is the waste of resources because statistically it is only a small fraction of the time when all the connections actually transmit traffic at the peak rate. If we design to share the bandwidth but not to share the buffer among connections, we have the rate envelope multiplexing case. This approach also called bufferless multiplexing because in the fluid modeling framework of this method, there is no need for a buffer. Indeed, in rate envelope multiplexing the target is that the total input rate is maintained below the capacity. The events of exceeding the capacity should be preserved below a certain probability, that is, P(λ_t > c) < ε, where λ_t is the input rate process, c is the link capacity, and ϵ is the allowed probability of exceeding the capacity. In actual practice, buffers always needed to store packets that arrive simultaneously (cell scale congestion). All the excess traffic is lost, and the overall loss rate is E[(λ_t − c)⁺/E(λ_t)]. The loss rate only depends on the stationary distribution of λ_t and not on its time-dependent properties. It is important because it means that the correlation structure has no effect on the loss rate. Therefore, the very difficult task of capturing traffic correlations (e.g., LRD) is not needed. The traffic structure can have impact on other performance measures but these can be neglected if the loss rate is small enough. For example, LRD traffic can yield to longer duration of the overloads than SRD (short-range dependence) traffic but using a small loss rate it can be neglected in practice. If we want to further increase the link utilization we have to share the buffer as well (Figure 2.1). This is the rate sharing method, also called buffered multiplexing.

Table 2.1 Main categories of open-loop traffic

Facility	Buffer sharing	Bandwidth sharing
Peak rate allocation	No	No
Rate envelope multiplexing	No	Yes
Rate sharing	Yes	Yes

The idea here is that by providing a buffer we can absorb some excess of the input rate. The excess of the queue length in the buffer at some level should be preserved below a certain probability, that is, P(Q > q) < ε, where q is the targeted queue length level, Q is the actual queue length, and ε is the allowed probability level of exceeding the targeted queue length. In this method much higher multiplexing gain and utilization can be achieved.

The main problem in rate sharing is that the loss rate realized with a given buffer size and link capacity depends in a complicated way on the traffic characteristics including also the correlation structure. As an example the loss and delay characteristics are rather difficult to compute if the input traffic is LRD. This is the reason for the admission control methods being much more complicated for rate sharing than for rate envelope multiplexing. Moreover, the disadvantage is not only the complex traffic control but the achievable utilization is also smaller in case of fractal traffic with strong SRD and LRD properties (see Figure 2.2).

Figure 2.1 Two solutions for buffered multiplexing.

Figure 2.2 Effect of correlation structure.

A large number of admission control strategies have been developed for both rate envelope multiplexing and rate sharing. It seems that the most powerful scheme is a kind of measurement-based admission control where the only traffic descriptor is the peak rate and the available rate is estimated in real time.

2.1.3.4  Closed-loop control of elastic traffic

Elastic traffic is generally controlled by reactive closed-loop traffic control methods. This is the principle of the TCP in the Internet and the ABR in the ATM. These protocols target at fully exploiting the available network bandwidth while keeping a fair share between contending traffic flows. Now we investigate the TCP as the general transfer protocol of the Internet. In TCP an additive increase, multiplicative decrease congestion avoidance algorithm has been implemented. If there is no packet loss the rate increases linearly but the packet transmission rate is halved whenever packet loss occurs. The algorithm tries to adjust its average rate to a value depending on the capacity and the current set of competing traffic flows on the links of its paths. The available bandwidth is shared in a roughly fair manner among the TCP flows.

A simple model of TCP, which also captures the fundamental behavior of the algorithm, is the well-known relationship between the flow throughput B and the packet loss rate $p:B(p)=c/(RTT\sqrt{p})$, where RTT is the TCP flow round-trip time and c is a constant. It should be noted that this simple formula is valid in case of a number of assumptions: RTT is constant, p is small (<1%), and the TCP source is greedy. The TCP mechanism is also assumed to be governed by the fast retransmit and recovery (no timeouts) and the slow-start phase is not modeled. More refined models were also developed but the square-root relationship between B and p seems to be the quite general rule of TCP.

We can conclude this section by stressing that the importance of choosing a good traffic model determines how successful we are in capturing the most important traffic characteristics. The basic question is the fundamental relationship among the traffic characteristics, network resources, and performance measures. Queuing models with some types of traffic models (e.g., Poisson, MMPP, MAP, etc.) are analytically tractable but others (e.g., ARIMA [autoregressive moving average], TES, FGN, etc.) are not. It remains a current research issue to develop new theoretical and applied tools to assist in solving teletraffic systems with the development of new and complex traffic models. Among them, the most promising seems to be those based on time series modeling.

2.1.4  Internet traffic times series modeling

The Internet traffic grows in complexity as the Internet becomes the universal communication network and conveys all kinds of information: from binary data to real-time video or interactive information. Evolving toward a multiservice network, its heterogeneity increases in terms of technologies, provisioning, and applications. The various networking functions (such as congestion control, traffic engineering, and buffer management) required for providing differentiated and guaranteed services involve a variety of timescales which, added to the natural variability of the Internet traffic, generate traffic properties that deviates from those accounted for by simple models. Therefore, a versatile model for Internet traffic that is able to capture its characteristics regardless of time, place, and aggregation level, is a step forward for monitoring and improving the Internet: for traffic management, charging, injecting realistic traffic in simulators, intrusion detection systems, etc.

Packets arrival processes are natural fine-grain models of computer network traffic. They have long been recognized as not being the Poisson (or renewal) processes, insofar as the interarrival delays are not independent. Therefore, nonstationary point processes or stationary Markov-modulated point processes have been proposed as models. However, the use of this fine granularity of modeling implies taking into account the large number of packets involved in any computer network traffic, hence huge data sets to manipulate. So a coarser description of the traffic is more convenient: the packet or byte-aggregated count processes. They are defined as the number of packets (bytes) that lives within the kth window of size Δ > 0, that is, whose time stamps lie between kΔ ≤ t_l < (k + 1)Δ; it will be noted as X_Δ(k). Therefore, an objective is the modeling of X_Δ(k) with a stationary process. Marginal distributions and auto covariance functions are then the two major characteristics that affect the network performance.

Due to the point process nature of the underlying traffic, Poisson or exponential distributions could be expected at small aggregation levels Δ; but it fails at larger aggregation levels. As X_Δ(k) is by definition a positive random variable, other works proposed to describe its marginal with common positive laws such as log-normal, Weibull or gamma distributions (Scherrer et al. 2007). For highly aggregated data, Gaussian distributions are used in many cases as relevant approximations. However, none of them can satisfactorily model traffic marginals both at small and large Δs. As it will be argued in this chapter, empirical studies suggest that a Gamma distribution Γ_{α, β} capture best the marginals of the X_Δ for a wide range of scales, providing a unified description over a wide range scales of aggregation Δ.

In Internet monitoring projects, traffic under normal conditions was observed to present large fluctuations in its throughput at all scales. This is often described in terms of long memory, self-similarity, and multifractality that impacts the second- (or higher-order) statistics. For computer network traffic, long memory or LRD property is an important feature as it seems to be related to decreases of the QoS as well as of the performance of the network, hence need to be modeled precisely. LRD is defined from the behavior at the origin of the power spectral density f_XΔ (ν) of the process:

$f_{X_{\text{Δ}}}\left(v\right)\approx C{\left|\text{v}\right|}^{-\text{ϒ}},\left|\text{v}\right|\to 0,0<\text{ϒ}<1$

Note that Poisson or Markov processes, or their declinations, are not easily suited to incorporate long memory. They may be useful in approximately modeling the LRD existing in the observation of a finite duration at the price of an increase in the number of adjustable parameters involved in the data description. But parsimony in describing data is indeed a much desired feature as it may be a necessary condition for a robust, meaningful and on-the-fly modeling. One can also incorporate long memory and short correlations directly into point processes using cluster point process models, yielding interesting description of the packet arrival processes. However, this model does not seem adjustable enough to encompass a large range of aggregation window size. An alternative relies on canonical long-range dependent processes such as fractional Brownian motion, fractional Gaussian noise, or Fractionally Autoregressive Integrated Moving Average (FARIMA). Due to the many different network mechanisms and various source characteristics, short-term dependencies also exist (superimposed to LRD) and play a central role. This leads to the idea to use the processes that have the same covariance as that of FARIMA models, as they contain both short- and long-range correlations.

A recurrent issue in traffic modeling lies in the choice of the relevant aggregation level Δ. This is an involved question whose answer mixes up the characteristics of the data themselves, the goal of the modeling as well as technical issues such as real time, buffer size, and computational cost constraints. Facing this difficulty of choosing a priori Δ, it is of great interest to have at disposal a statistical model that may be relevant for a large range of values of Δ. One approach is the joint modeling of the marginal distribution and the covariance structure of Internet traffic time series, in order to capture both their non-Gaussian and long-memory features. For this purpose, the best solution is to choose a non-Gaussian long-memory process whose marginal distribution is a gamma law and whose correlation structure is the one of a FARIMA process.

2.2  Renewal traffic models

This section presents briefly the characteristics of the renewal traffic processes, and more specific the Poisson and Bernoulli processes.

The renewal models were first used due to their mathematic simplicity. In a renewal traffic process, A_n is independent and identically distributed (i.i.d), but the distribution law can be a general one (Clark and Schimmel 2004). Unfortunately, with a few exceptions, the superposition of the independent renewal processes does not generate a new renewal process. But the mentioned exceptions have an important place in the theory and the practice of traffic description, especially those based on queues. On the other hand, the renewal processes, despite their analytic simplicity, have a main modeling drawback—the self-correlation function of {A_n} disappears for all nonzero lags and so the important role of the self-correlation as statistically representative of the temporal dependence of the time series is lost. It has to be noted that a positive self-correlation of {A_n} can explain the traffic variability. A variable (bursty) traffic is dominant in broadband networks and when this traffic is present in a queue system the performance (such as mean waiting times) is altered in comparison with that of the renewal traffic (which lacks temporal dependence). For these reasons, the models that capture the self-correlated nature of the traffic are essential for the prediction of the large scale networks performance.

2.2.1  Poisson processes

Poisson models are the oldest traffic models, dating back to the advent of telephony and the renowned pioneering telephone engineer, A. K. Erlang. In traditional queuing theory, the Poisson arrival process has been a favorite traffic model for data and voice. The traditional assumption of Poisson arrivals has been often justified by arguing that the aggregation of many independent and identically distributed renewal processes tends to a Poisson process when the number increases.

A Poisson process can be characterized as a renewal process whose interarrival times {A,} are exponentially distributed with rate parameter λ, that is, P{A_n ≤ t} = 1 − exp(–λt). Equivalently, it is a counting process, satisfying P{N(t) = n} = exp(–λt)(λt)ⁿ/n!, and the number of arrivals in disjoint intervals is statistically independent (a property known as independent increments). Poisson processes enjoy some elegant analytical properties. First, the superposition of independent Poisson processes results in a new Poisson process whose rate is the sum of the component rates. Second, the independent increment property renders Poisson process without memory. This, in turn, greatly simplifies queuing problems involving Poisson arrivals. Third, Poisson processes are fairly common in traffic applications that physically comprise a large number of independent traffic streams, each of which may be quite general. The theoretical basis for this phenomenon is known as Palm’s theorem (Arrowsmith et al. 2005). It roughly states that under suitable but mild regularity conditions, such multiplexed streams approach a Poisson process as the number of streams grows, but the individual rates decrease so as to keep the aggregate rate constant. Thus, traffic streams on main communications arteries are commonly believed to follow a Poisson process, as opposed to traffic on upstream tributaries, which are less likely to be Poisson. However, traffic aggregation need not always result in a Poisson stream. Time-dependent Poisson processes are defined by letting the rate parameter λ depend on time. Compound Poisson processes are defined in the obvious way, by specifying the distribution of the batch size, B_n, independent of A_n.

Despite the attractiveness of the Poisson model, its validity in real-time traffic scenario has been often questioned. Barakat et al. offered evidence that flow arrivals on Internet backbone links are well matched by a Poisson process (Barabási and Bonabeau 2003). For large populations where each user is independently contributing a small portion of the overall traffic, user sessions can be assumed to follow a Poisson arrival process (Roberts 2001). Based on traces of wide-area TCP traffic, Poisson arrivals appears to be suitable for traffic at the session level when sessions are human initiated, for example, interactive FTP sessions (Paxson and Floyd 1994). However, the Poisson model does not hold for machine-initiated sessions or for any packet-level traffic.

2.2.2  Bernoulli processes

Bernoulli processes are the discrete-time analog of the Poisson processes (time-dependent and compound Bernoulli processes are defined in the natural way). A Bernoulli process is a finite or infinite sequence of independent random variables X₁, X₂, X₃, …, such that

•  For each i, the value of X_i is either 0 or 1

•  For all values of i, the probability that X_i = 1 is the same number p

In other words, a Bernoulli process is a sequence of independent identically distributed Bernoulli trials. Independence of the trials implies that the process is without memory. Given that the probability p is known, past outcomes provide no information about future outcomes. If the process is infinite, then from any point the future trials constitute a Bernoulli process identical to the whole process, the fresh-start property. Considering the probability of an arrival in any time slot is p, independent of any other one, it follows that for slot k, the corresponding number of arrivals is binomial, and between 0 and k we have $P\left\{N_k=n\right\}=\left({}_n^k\right)p^n{\left(1-p\right)}^{k-n}$. The time between arrivals is geometric with parameter $p:P\left\{A_n=j\right\}=p{\left(1-p\right)}^j$ being a nonnegative integer.

2.2.3  Phase-type renewal processes

An important special case of renewal models occurs when the interarrival times are of the so-called phase type. Phase-type interarrival times can be modeled as the time to absorption in a continuous-time Markov process $C={\left\{C\left(t\right)\right\}}_{t=0}^{\infty }$ with state space {0, 1, …, m}; here, state 0 is absorbing, all other states are transient, and absorption is guaranteed in a finite time. To determine A_n, start the process C with some initial distribution π. When absorption occurs (i.e., when the process enters state 0), stop the process. The elapsed time is A_n which implies that it is a probabilistic mixture of sums of exponentials. Then, restart with the same initial distribution π and repeat the procedure independently to get A_n+1. Phase-type renewal processes give rise to relatively tractable traffic models. They also enjoy the property that any interarrival distribution can be approximated arbitrarily closely by phase-type distributions.

2.3  Markov traffic models

Unlike renewal traffic models, Markov and Markov-renewal traffic models introduce dependence into the random sequence {A_n}. Consequently, they can potentially capture traffic burstiness, because of nonzero autocorrelations in {A_n}.

Let consider a continuous-time Markov process $M={\left\{M\left(t\right)\right\}}_{t=0}^{\infty }$ with a discrete-state space. In this case, M behaves as follows: it stays in a state i for an exponentially distributed holding time with parameter λ_i, which depends on i alone; it then jumps to state j with probability p_ij, such that the matrix P = [p_ij] is a probability matrix. In a simple Markov traffic model, each jump of the Markov process is interpreted as signaling an arrival, so interarrival times are exponential, and their rate parameters depend on the state from with the jump occurred. This results in dependence among interarrival times as a consequence of the Markov property. Markov models in slotted time can be defined for the process {A_n} in terms of a Markov transition matrix P = [p_ij]. Here, state i corresponds to i idle slots separating successive arrivals, and p_ij is the probability of a j-slot separation, given that the previous one was an i-slot separation. Arrivals may be single units, a batch of units, or a continuous quantity. Batches may themselves be described by a Markov chain, whereas continuous-state, discrete-time Markov processes can model the (random) workload arriving synchronously at the system. In all cases, the Markov property introduces dependence into interarrival separation, batch sizes and successive workloads, respectively.

Markov-renewal models are more general than discrete-state Markov processes, yet retain a measure of simplicity and analytical tractability. A Markov-renewal process $R={\left\{\left(M_n,{\text{τ}}_n\right)\right\}}_{n=0}^{\infty }$, is defined by a Markov chain {M_n} and its associated jump times {τ_n}, subject to the following constraint: the pair (M_n+1, τ_n+1) of next state and interjump time depends only on the current state M_n, but neither on previous states nor on the previous interjump times. Again, if we interpret jumps (transitions) of {M_n} as signaling arrivals, we would have dependence on the arrival process. Also, unlike in the case of the Markov process, the interarrival times can be arbitrarily distributed, and these distributions depend on both states straddling each interarrival interval.

The Markovian arrival process (MAP) is a broad and versatile subclass of Markov-renewal traffic processes, enjoying analytical tractability. Here, the interarrival times are phase-type but with a wrinkle: traffic arrivals still occur at absorption instants of the auxiliary Markov process M, but the latter is not restarted with the same initial distribution; rather, the restart state depends on the previous transient state from which absorption had just occurred. While MAP is analytically simple, it enjoys considerable versatility. Its formulation includes Poisson processes, phase-type renewal processes, and others as special cases (Roberts 2004). It also has the property that the superposition of independent MAP traffic streams results in a MAP traffic stream governed by a Markov process whose state space is the cross-product of the component state spaces.

2.3.1  Markov-modulated traffic models

Markov-modulated models constitute an extremely important class of traffic models. The idea is to introduce an explicit notion of state into the description of a traffic stream: an auxiliary Markov process is evolving in time and its current state modulates the probability law of the traffic mechanism. Let $M={\left\{M\left(t\right)\right\}}_{t=0}^{\infty }$ be a continuous-time Markov process, with state space 1,2, …, m. Now assume that while M is in state k, the probability law of traffic arrivals is completely determined by k, and this holds for every 1 ≤ k ≤ m. Note that when M undergoes a transition to, say, state j, then a new probability law for arrivals takes effect for the duration of state j, and so on. Thus, the probability law for arrivals is modulated by the state of M (such systems are also called doubly stochastic [Frost and Melamed 1994], but the term “Markov modulation” makes it clear that the traffic is stochastically subordinated to M). The modulating process certainly can be more complicated than a continuous-time, discrete-state Markov process (so the holding times need not be restricted to exponential random variables), but such models are far less analytically tractable. For example, Markov-renewal modulated processes constitute a natural generalization of Markov-modulated processes with generally distributed interarrival times.

2.3.2  Markov-modulated Poisson process

The most commonly used Markov-modulated model is the Markov-modulated Poisson process (MMPP) model, which combines the simplicity of the modulating Markov process with that of the modulated Poisson process. In this case, the modulation mechanism simply stipulates that in state k of M, arrivals occur according to a Poisson process at rate λ_k. As the state changes, so does the rate. MMPP models can be used in a number of ways. Consider first a single traffic source with a variable rate. A simple traffic model would quantize the rate into a finite number of rates, and each rate would give rise to a state in some Markov modulating process. It remains to be verified that exponential holding times of rates are an appropriate description, but the Markov transition matrix Q = [Q_kj] can be easily estimated from an empirical data: simply quantize the empirical data, and then estimate Q_kj, by calculating the fraction of times that M switched from state k to state j.

As a simple example, consider a two-state MMPP model, where one state is an “on” state with an associated positive Poisson rate, and the other is an “off” state with associated rate zero (such models are also known as interrupted Poisson). These models have been widely used to model voice traffic sources; the “on” state corresponds to a talk spurt (when the speaker emits sound), and the “off” state corresponds to a silence (when the speaker pauses for a break). This basic MMPP model can be extended to aggregations of independent traffic sources, each of which is an MMPP, modulated by an individual Markov process M_i, as described previously.

Let J(t) = (J₁(t), J₂(t), …, J_r(t)), where J_i(t) is the number of active sources of traffic type i, and let M(t) = (M₁(t), M₂(t), …, M_r(t)) be the corresponding vector-valued Markov process taking values on all r-dimensional vectors with nonnegative integer components. The arrival rate of class i traffic in state (j₁, j₂, …, j_r) of M(t) is j_iλ_i.

2.3.3  Transition-modulated processes

Transition-modulated processes are a variation of the state modulation idea. Essentially, the modulating agent is a state transition rather than a state. A state transition, however, can be described simply by a pair of states, whose components are the one before transition and the one after it. The generalization of a transition-modulated traffic model to continuous time is straightforward (Adas 1997). Let $M={\left\{M_n\right\}}_{n=1}^{\infty }$ be a discrete-time Markov process on the positive integers. State transitions occur on slot boundaries, and are governed by an m×m Markov transition matrix P = [P_ij]. Let B_n denote the number of arrivals in slot n, and assume that the probabilities $P\left\{B_n=k|M_n=i,M_{n+1}=j\right\}=t_{ij}\left(k\right)$, are independent of any past state information (the parameters t_ij(k) are assumed given). Notice that these probabilities are conditioned on transitions (M_n, M_n+1) of M from state M_n to state M_n+1 during slot n. Furthermore, the number of traffic arrivals during slot n is completely determined by the transition of the modulating chain through the parameters t_ij(k).

Markov-modulated traffic models are a special case of Markovian transition-modulated ones: simply take the special case when the conditioning event is {M_n = i}. That is, t_ij(t) = t_i(t) depends only on the state i of the modulating chain in slot n, but is independent of its state j in the next slot n + 1. Conversely, Markovian transition-modulated processes can be thought of as Markov-modulated ones, but on a larger state space. Indeed, if {M_n} is Markov, so is the process {M_n, M_n+1} of its transitions.

As before, multiple transition-modulated traffic models can be defined, one for each traffic class of interest. The complete traffic model is obtained as the superposition of the individual traffic models.

2.4  Fluid traffic models

The fluid traffic concept dispenses with the individual traffic units. Instead, it views traffic as a stream of fluid, characterized by a flow rate (such as bits per second), so that a traffic count is replaced by a traffic volume. Fluid models are appropriate to cases where individual units are numerous relative to a chosen timescale. In other words, an individual unit is by itself of little significance, just as one molecule more or less in a water pipeline has but an infinitesimal effect on the flow. In the B-ISDN context of ATM, all packets are fixed-size cells of relatively short length (53 bytes); in addition, the high transmission speeds (say, on the order of a gigabit per second) render the transmission impact of an individual cell negligible. The analogy of a cell to a fluid molecule is a plausible one. To further highlight this analogy, contrast an ATM cell with a much bigger transmission unit, such as a coded (compressed) high-quality video frame, which may consist of a thousand cells. A traffic arrival stream of coded frames should be modeled as a discrete stream of arrivals, because such frames are typically transmitted at the rate of 30 frames per second. A fluid model, however, is appropriate for the constituent cells. Although an important advantage of fluid models is their conceptual simplicity, important benefits will also accrue to a simulation model of fluid traffic. As an example, consider again a broadband ATM scenario. If one is to distinguish among cells, then each of them would have to count as an event. The time granularity of event processing would be quite fine, and consequently, processing cell arrivals would consume vast CPU and possibly memory resources, even on simulated timescales of minutes. A statistically meaningful simulation may often be infeasible. In contrast, a fluid simulation would assume that the incoming fluid flow remains (roughly) constant over much longer time periods. Traffic fluctuations are modeled by events signaling a change of flow rate. Because these changes can be assumed to happen far less frequently than individual cell arrivals, one can realize enormous savings in computing. In fact, infeasible simulations of cell arrival models can be replaced by feasible simulations of fluid models of comparable accuracy. In a queuing context, it is easy to manipulate fluid buffers. Furthermore, the waiting time concept simply becomes the time it takes to serve (clear) the current buffer, and loss probabilities (at a finite buffer) can be calculated in terms of overflow volumes. Because fluid models assume a deterministic service rate, these statistics can be readily computed. Typically, though, larger traffic units (such as coded frames) are of greater interest than individual cells. Modeling the larger units as discrete traffic and their transport as fluid flow would give us the best of both worlds: we can measure waiting times and loss probabilities and enjoy savings on simulation computing resources.

Typical fluid models assume that sources are bursty—of the “on–off” type. While in the “off” state, traffic is switched off, whereas in the “on” state traffic arrives deterministically at a constant rate L. For analytical tractability, the duration of “on” and “off” periods are assumed to be exponentially distributed and mutually independent (i.e., they form an alternating renewal process) (Jagerman et al. 1997). Fluid traffic models of these types can be analyzed as Markov-modulated constant rate traffic. The host of generalizations, described above for MMPP, carries over to fluid models as well, including multiple sources and multiple classes of sources.

2.5  Autoregressive traffic models

Autoregressive models define the next random variable in the sequence as an explicit function of previous ones within a time window stretching from the present into the past. Such models are particularly suitable for modeling processes which are large consumers of bandwidth in emerging high-speed communications networks, such as VBR-coded video. The nature of video frames is such that successive frames within a video scene vary visually very little (recall that there are 30 frames per second in a high-quality video). Only scene changes (and other visual discontinuities) can cause abrupt changes in frame bit rate. Thus, the sequence of bit rates (frame sizes) comprising a video scene may be modeled by an autoregressive scheme, while scene changes can be modeled by some modulating mechanism, such as a Markov chain.

2.5.1  Linear autoregressive models (AR)

The class of linear autoregressive models has the form

$\begin{array}{cc}{X}_n=a_0+{\displaystyle \sum _{r=1}^p{a}_r{X}_{n-r}+{\text{ε}}_n,}& n>0,\end{array}$

(2.2)

where (X_–p+1, …, X₀) are prescribed random variables, a_r (0 ≤ r ≤ p) are real constants and ε_n are zero mean, IID random variables, called residuals, which are independent of the X_n. Equation 2.2 describes the simplest form of a linear autoregression scheme, called AR(p), where p is the order of the auto regression. In a good model, the residuals ought to be of a smaller magnitude than the X_n, in order to explain the empirical data. The recursive form in Equation 2.2 makes it clear how to randomly generate the next random element in the sequence ${\left\{X_n\right\}}_{n=0}^{\infty }$ from a previous one: this simplicity makes AR schemes popular candidates for modeling auto-correlated traffic. A simple AR(2) model has been used to model variable bit rate (VBR) coded video (Dobrescu et al. 2004a). More elaborate models can be constructed out of AR(p) models combined with other schemes. For example, video bit rate traffic was modeled as a sum R_n = X_n + Y_n + K_nC_n, where the first two terms comprise independent AR(1) schemes and the third term is a product of a simple Markov chain and an independent normal variate from an IID normal sequence (Ramamurthy and Sengupta 1992). The purpose of having two autoregressive schemes was to achieve a better fit to the empirical autocorrelation function; the third term was designed to capture sample path spikes due to video scene changes.

Autoregressive series are important because (1) they have a natural interpretation—the next value observed is a slight perturbation of a simple function of the most recent observations; (2) it is easy to estimate their parameters, usually with standard regression software; and (3) they are easy to forecast—again the standard regression software will do the job.

2.5.2  Moving average series (MA) models

The time series described by the model

$\begin{array}{cc}{X}_n={\displaystyle \sum _{r=0}^q{b}_r{\text{ε}}_{n-r},}& n>0,\end{array}$

(2.3)

is said to be a moving average process of order q − MA(q)—where b_r (0 ≤ r ≤ q), are real constants and ε_n are uncorrelated random variables with null average (white noise). No additional conditions are required to ensure stationarity. Note that it is easy to distinguish MA and AR series by the behavior of their autocorrelation functions (acf). The acf for MA series “cuts off” sharply while that for an AR series, it decays exponentially (with a possible sinusoidal ripple superimposed).

2.5.3  Autoregressive moving average series (ARMA) models

Modeling stationary and reversible processes using AR or MA series necessitate often the estimation of a large number of parameters, which reduces the estimation efficiency. In order to minimize this impediment, one can combine (2.2) and (2.3) in a mix model:

$X_n=a_0+{\displaystyle \sum _{r=1}^p{a}_r{X}_{n-r}}+{\displaystyle \sum _{r=0}^q{b}_r{\text{ε}}_{n-r}}.$

(2.4)

The class of series having models of Equation 2.4 type is named ARMA(p, q) and referred to as autoregressive moving average series of order (p, q). Stationarity can be checked by examining the roots of the characteristic polynomial of the AR operator and model parametrization can be checked by examining the roots of the characteristic polynomial of the MA operator.

2.5.4  Integrated ARIMA models

An integrated autoregressive moving average (p, d, q) series, denoted as ARIMA(p, d, q), is closely related to ARMA(p, q) and can be obtain by substituting X_n in Equation 2.4 with the d-difference of the series {X_n}. ARIMA models are more general as ARMA models and include some nonstationary series. The term “integrated” denotes that the ARMA model is first approximated to the differentiate data and then added to form the target nonstationary ARIMA model. Therefore, a ARMA(p, q) process can be seen as a ARIMA(p, 0, q) process, and the random walk process can be seen as an ARIMA(0,1,0) process. It has to be noted that both ARMA and ARIMA series have autocorrelation functions with geometric decay, that is, ρ(n) ~ rⁿ for 0 < r < 1, when n → ∞ and consequently can be used in the study of processes with short-range dependence.

2.5.5  FARIMA models

FARIMA processes are the natural generalizations of standard ARIMA (p, d, q) processes when the degree of differencing d is allowed to take non-integral values (Liu et al. 1999). A FARIMA(p, d, q) process {X_t: t = …, − 1, 0, 1,…} is defined as

$\text{Φ}\left(B\right){\text{Δ}}^d{X}_t=\text{Θ}\left(B\right)a_t$

(2.5)

where {a_t} is a white noise and $d\in \left(-0.5,0.5\right),\text{Φ}\left(B\right)=1-{\text{φ}}_{1}B-{\text{φ}}_2{B}^2-\dots {\text{φ}}_p{B}^p$ and $\text{Θ}\left(B\right)=1-{\text{θ}}_{1}B-{\text{θ}}_2{B}^2-\dots -{\text{θ}}_q{B}^q.\text{Φ}\left(B\right),\text{Θ}\left(B\right)$ have no common zeroes, and also no zeroes in |B| ≤ 1 while p and q are nonnegative integers. B is the backward-shift operator, that is, BX_t = X_t−1 Δ = 1 − B is the differencing operator and Δ^d denotes the fractional differencing operator, ${\text{Δ}}^d={\left(1-B\right)}^d={\displaystyle {\sum }_{k=0}\left(\begin{array}{c}a\\ k\end{array}\right){(-B)}^k;}\left(\begin{array}{c}d\\ k\end{array}\right)=\text{Γ}(d+1)/[\text{Γ}(k+1)\text{Γ}(d-k+1)]$; Γ denotes the Gamma function.

Clearly, if d = 0, FARIMA(p, d, q) processes are the usual ARMA(p, q) processes. If d ∈ (0, 0.5), then LRD or persistence occurs in the FARIMA processes. FARIMA(0,d,0) process, that is, fractional differencing noise (FDN), is the simplest and most fundamental form of the FARIMA processes. The property of FARIMA(0,d,0) process is similar to fractional Gaussian noise (FGN) process, which can only describe LRD. The parameter d in FARIMA(0,d,0) process is the indicator for the strength of LRD, just like the Hurst parameter H in FGN process. In fact, H = d + 0.5. Both processes have autocorrelation functions which behave asymptotically as k^2d–1 with different constants of proportionality.

For d ∈ (0, 0.5), p ≠ 0 and q ≠ 0, a FARIMA(p, d, q) process can be regarded as an ARMA(p, q) process driven by FDN. From Equation 2.1, we obtain X_t = Φ⁻¹(B)Θ(B)ϒ_t, where ϒ_t = Δ^–da_t. Here, ϒ_t is a FDN. Consequently, compared with ARMA and FGN processes, the FARIMA(p, d, q) processes are flexible and parsimonious with regard to the simultaneous modeling of the long- and short-range dependent behavior of a time series.

2.6  TES traffic models

2.6.1  TES processes

Transform-expand-sample (TES) models provide another modeling approach geared toward capturing both marginals and autocorrelations of empirical records simultaneously, including traffic. The empirical TES methodology assumes that some stationary empirical time series (such as traffic measurements over time) is available. It aims to construct a model satisfying the following three fidelity requirements: (1) The model’s marginal distribution should match its empirical counterpart (a histogram, in practice). (2) The model’s leading autocorrelations should approximate their empirical counterparts up to a reasonable lag. (3) The sample path realizations generated by simulating the model should correspond to the empirical records. The first two are precise quantitative requirements, whereas the third is a heuristic qualitative one. Nevertheless, it is worth adopting this subjective requirement and keeping its interpretation at the intuitive level; after all, common sense tells us that if a model gives rise to time series which are entirely divorced in “appearance” from the observed ones, then this would weaken our confidence in the model, and vice versa.

TES processes are classified into two categories: TES⁺ and TES⁻. The superscript (plus or minus) is a mnemonic reminder of the fact that they give rise to TES processes with positive and negative lag-1 autocorrelations, respectively. TES models consist of two stochastic processes in lockstep, called background and foreground sequences, respectively. Background TES sequences have the form:

$\begin{array}{cc}{U}_n^{+}=\{\begin{array}{ll}{U}_0,\hfill & n=0\hfill \\ \langle U_{n-1}^{+}+V_n\rangle ,\hfill & n>0\hfill \end{array}& U_n^{-}=\{\begin{array}{ll}{U}_n^{+},\hfill & n-\text{even}\hfill \\ 1-U_n^{+},\hfill & n-\text{odd}\hfill \end{array}\end{array}$

(2.6)

Here, U₀ is distributed uniformly on $[0,1);{\left\{V_n\right\}}_{n=1}^{\infty }$ is a sequence of IID random variables, independent of U₀, called the innovation sequence, and angular brackets denote the modulo-1 (fractional part) operator 〈x〉 = x − max{integer n:n ≤ x}.

Background sequences play an auxiliary role. The real targets are the foreground sequences: $X_n^{+}=D\left(U_n^{+}\right),X_n^{-}=D\left(U_n^{-}\right)$ where D is a transformation from [0,1) to the reals, called a distortion. It can be shown that all background sequences are Markovian stationary, and their marginal distribution is uniform on [0,1), regardless of the probability law of the innovations {V_n}. However, the transition structure $\left\{U_n^{+}\right\}$ is time invariant, while that of $\left\{U_n^{-}\right\}$ is time-dependent. The inversion method allows us to transform any background uniform variates to foreground ones with an arbitrary marginal distribution. To illustrate this idea, consider an empirical time series ${\left\{{\Upsilon }_n\right\}}_{n=0}^N$ from which one computes an empirical density ${\widehat{h}}_{\Upsilon }$ and its associated distribution function ${\widehat{H}}_{\Upsilon }$. Then, the random variable $X={\widehat{H}}_{\Upsilon }^{-1}\left(U\right)$ has the density ${\widehat{h}}_{\Upsilon }$. Thus, TES foreground sequences can match any empirical distribution.

2.6.2  Empirical TES methodology

The empirical TES methodology actually employs a composite two-stage distortion:

$\begin{array}{cc}{D}_{\Upsilon ,\text{ξ}}\left(x\right)={\widehat{H}}_{\Upsilon }^{-1}\left(S_{\text{ξ}}\left(x\right)\right),& x\in [0,1)\end{array}$

(2.7)

where ${\widehat{H}}_{\Upsilon }^{-1}$ is the inverse of the empirical histogram distribution based on ϒ, and S_ξ is a “smoothing” operation, called a stitching transformation, parameterized by 0 < ξ < 1, and given by:

$S_{\text{ξ}}\left(x\right)=\{\begin{array}{ll}y/\text{ξ},\hfill & 0\le y<\text{ξ}\hfill \\ \left(1-y\right)/\left(1-\text{ξ}\right),\hfill & \text{ξ}\le y<1\hfill \end{array}$

(2.8)

For 0 < ξ < 1, the effect of S_ξ is to render the sample paths of background TES sequences more “continuous-looking.” Because stitching transformations preserve uniformity, the inversion method via ${\widehat{H}}_{\Upsilon }^{-1}$ guarantees that the corresponding foreground sequence would have the prescribed marginal distribution ${\widehat{H}}_{\Upsilon }$. The empirical TES modeling methodology takes advantage of this fact which effectively decouples the fitting requirements of the empirical distribution and the empirical autocorrelation function. Because the former is automatically guaranteed by TES, one can concentrate on fitting the latter. This is carried out by a heuristic search for a pair (ξ, f_V), where ξ is a stitching parameter and f_V is an innovation density; the search is declared a success on finding that the corresponding TES sequence gives rise to an autocorrelation function that adequately approximates its empirical counterpart, and whose simulated sample paths bear “adequate resemblance” to their empirical counterparts.

Stationary TES models can be combined to yield nonstationary composite ones. MPEG-coded video is such a case. It consists of three kinds of frames (called I-frames, P-frames, and B-frames), interleaved in a deterministically repeating sequence (the basic cycle starts with an I-frame and ends just short of the next 1-frame). Consequently, MPEG-coded VBR video is nonstationary, even if the corresponding I, P, and B subsequences of frames are stationary. A composite TES model can be obtained by modeling the I, B, and P subsequences separately, and then multiplexing the three streams in the correct order. The resulting multiplexed TES model obtained from the corresponding TES models of the subsequences, but with autocorrelation injected into frames within the same cycle. Although the autocorrelation functions and spectral densities were formally computed from a single sample path as if the MPEG sequences were stationary, and therefore represent averaged estimates of different correlation coefficients, they nevertheless give an indication of how well the composite TES model captured temporal dependence in the empirical data, because they were all computed from sample paths in the same way. The general good agreement between the TES model statistics and their empirical counterparts is in accord with the three fidelity requirements stipulated at the beginning of this section. These TES source models can be used to generate synthetic streams of realistic traffic to drive simulations of communications networks.

2.7  Self-similar traffic models

In the last 20 years, studies of high-quality, high-resolution traffic measurements have revealed a new phenomenon with potentially important ramifications to the modeling, design, and control of broadband networks. These works started with classical experiments, for example an analysis of hundreds of millions of observed packets over an Ethernet LAN in a R&D environment (Leland et al. 1993) or an analysis of a few millions of observed frame data generated by VBR video services (Beran 1994). In these studies, packet traffic appears to be statistically self-similar. A self-similar (or fractal) phenomenon exhibits structural similarities across all (or at least a wide range) of the timescales. In the case of packet traffic, self-similarity is manifested in the absence of a natural length of a burst: at every timescale ranging from a few milliseconds to minutes and hours, similar-looking traffic bursts are evident. Self-similar stochastic models include fractional Gaussian noise and FARIMA processes. Self-similarity manifests itself in a variety of different ways: a spectral density that diverges at the origin (1/f^α noise, 0 < α < l), an on-summable autocorrelation function (indicating LRD), and a variance of the sample mean that decreases (as a function of the sample size n) more slowly than l/n. The key parameter characterizing these phenomena is the so-called Hurst parameter, H, which is designed to capture the degree of self-similarity in a given empirical record as follows.

Let ${\left\{{\Upsilon }_k\right\}}_{k=1}^N$ be an empirical time series with sample mean ϒ(n) and sample variance S²(n). The rescaled adjusted range, or R/S statistic, is given by R(n)/S(n) with:

$R\left(N\right)=\max \left\{{\displaystyle \sum _{i=1}^k\left({\Upsilon }_i-\overline{\Upsilon }\left(n\right)\right),1\le k\le n}\right\}-\min \left\{{\displaystyle \sum _{i=1}^k\left({\Upsilon }_i-\overline{\Upsilon }\left(n\right)\right),1\le k\le n}\right\}$

It has been found empirically that many naturally occurring time series appear to obey the relation: E[R(n)/S(n)] = n^H, with n being large, the H value typically about 0.73. On the other hand, for renewal and Markovian sequences, it can be shown that the previous equation holds with H = 0.5, for large n. This discrepancy, generally referred to as the Hurst phenomenon, is a measure of the degree of self-similarity in time series, and can be estimated from empirical data. From a mathematical point of view, self-similar traffic differs from other traffic models in the following way. Lets be a time unit representing a timescale, such as s = 10^m seconds (m = 0, ±1, ±2, …). For every timescale s, let $X^{\left(s\right)}=\left\{X_n^{\left(s\right)}\right\}$ denote the time series computed as the number of units (packets, bytes, cells, etc.) per time units in the traffic stream. Traditional traffic models have the property that, as s increases, the aggregated processes, X^(s) end to a sequence of IID random variables (covariance stationary white noise).

On the other hand, the corresponding aggregation procedure of empirical traffic data yields time series X^(s), which reveal two related types of behavior, when plotted against time. They either appear visually indistinguishable from one another (“exactly self-similar”) but distinctively different from pure noise, or they converge to a time series with a nonde-generate autocorrelation structure (“asymptotically self-similar”).

In contrast, simulations of traditional traffic models, rapidly converge to white noise after increasing the timescale by about two or three orders of magnitude. Similarly, when trying to fit traditional traffic models to self-similar traffic data, the number of parameters required typically grows, as the sample size increases. In contrast, self-similar traffic models are able to capture the observed fractal nature of packet traffic in a parsimonious manner (with about one to four parameters). Parameter estimation techniques are available for many self-similar models, as well as Monte Carlo methods for generating long traces of synthetic self-similar traffic.

Potential implications of self-similar traffic on issues related to design, control, and performance of high-speed, cell-based networks are currently under study, especially because it was shown that many of the commonly used measures for burstiness do not characterize self-similar traffic.

Contrary to commonly held beliefs that multiplexing traffic streams tends to produce smoothed out aggregate traffic with reduced burstiness, aggregating self-similar traffic streams can actually intensify burstiness rather than diminish it.

From a practical vantage point, there are also indications that traffic congestion in self-similar networks may have broadly differing characteristics from those produced by traditional traffic models. All these aspects will be detailed in Chapter 3.