chapter four

Topological models of complex networks

4.1  Topology of large-scale networks

The study of a majority of complex networks started initially from the desire to understand various natural systems, ranging from communication networks to ecologic chains or networks (Costa et al. 2003). This chapter lists the significant results in the research of complex networks, focusing on the large-scale traffic networks. Beyond the fields from where data was extracted, special emphasis will be placed on the three robust indicators for network topology: average path length, clustering coefficient, and degree distribution. To model a distributed network environment like the Internet, it is necessary to integrate the data collected from multiple points in a network in order to get a complete picture of network-wide view of the traffic. Knowledge of dynamic characteristics is essential to network management (e.g., detection of failures/congestion, provisioning, and traffic engineering like QoS routing or server selections). However, given the enormity of the huge scale and restrictions due to access rights, it is expensive (sometime impossible) to measure such characteristics directly. To solve this problem, a host of methods and tools to infer the unobservable network performance characteristics are used in large-scale networking environment. A model where inference based on self-similarity and fractal behavior is best represented is the scale-free network, and so this model will be largely discussed in this chapter.

4.1.1  World Wide Web

The World Wide Web (WWW) network is the biggest example of providing topological information. Its nodes are the documents (web pages) and its edges are the hyperlinks (URL) connecting one document to another. The interest in the WWW as a network simply exploded after discovering that the distribution of the degrees of the Web pages is given by a power law over several magnitudes (Barabási et al. 1999). Moreover, the cited work, supplemented and developed in Albert and Barabási (2002) paved the way for extensive research based on rigorous mathematical models. Because the edges of the WWW graph are directed, the network is defined by a two-degree distribution: output arcs’ degree P_out(k), which is the probability for a document to have k URL links to other documents, and the input arcs’ degree P_in(k), which is the probability that k URL link to indicate to a certain document. Several studies reported that both P_out(k) and P_in(k) have power law queues:

$\begin{array}{ccc}{P}_{\text{out}}\left(k\right)~k^{-{\Upsilon }_{\text{out}}}& \text{and}& P_{\text{in}}\left(k\right)~k^{-{\Upsilon }_{\text{in}}}\end{array}$

(4.1)

Albert, Jeong, and Barabási (2000) studied a subset of the WWW containing 325,729 nodes and found that ϒ_out = 2.45 and ϒ_in = 2.1. Other researchers used a slightly different representation of the WWW, treating every node as a domain name and considering that any two nodes are connected if a page from one refers to a page in the other. Although this method often associates thousands of pages belonging to the same domain, being a nontrivial node aggregation, the distribution of the outgoing arcs still follows a power law equal to ${\text{ϒ}}_{\text{in}}^{\text{dom}}=1.94$.

The oriented nature of the WWW does not allow for measuring the clustering coefficient using Equation 4.1. A way to circumvent this problem is to transform the network in an unoriented direction, by considering each edge to be bidirectional. The original algorithms for constructing these styles of network are used for undirected graphs. Among them, small world (SW) undirected networks were first constructed by Watts and Strogatz using an algorithm described as a rewiring ring lattice (Watts and Strogatz 1998). Then, Kleinberg proposed a directed version of SW networks, which starts from a two-dimensional grid rather than a ring in his work searching for a decentralized algorithm to find shortest paths in directed SW (Kleinberg 2000). More recently, Sriram and Cliff suggested a hybrid approach closer to of Watts and Strogatz’s original algorithm with the only modification that the initial condition is a ring lattice with outgoing directed edges to all k nearest neighbors, with k being the number of subscriptions in their model (Sriram and Cliff 2011). Thus, between neighboring edges, there will be two edges, one in each direction. As rewiring probability p = 0.1 was used, a value Watts and Strogatz showed to be large enough to exhibit short path lengths, and at the same time small enough to exhibit a high transitivity of the network.

The Web exhibits properties that identify it as a complex network. Incorporating the small world, scale-free, self-organizing properties of the Web, a theoretical framework for understanding and mapping the movement of information on such dynamic information system explores the Web using complexity and fractal theories to explain the underlying structure of the Web. In the previous years, complexity theory offers new ways to understand the evolution, topology, and relationships that comprise real networks, including the Internet and the WWW. These seemingly chaotic networks develop in ways that are self-similar, self-sustaining, and self-regulating. They have the same patterns at different scales, can replicate themselves, correct errors, and organize without central authority. Complexity theory offers a new insight to phenomena that were previously thought to be random, chaotic, or too complex to understand. Much research has been done to articulate and formalize the revolutionary ideas that explain and model the chaos, the idea that stochastic outcomes are based on the repeating relationships of simple patterns. The best models accurately and simply represent real-world phenomena dynamically. In the case of a dynamic system, however, modeling part of the system does little to facilitate our knowledge of the entire system, as the parts functioning together are frequently more revealing than the sum of the individual aspects. The ability of building this functionality, bringing together concepts from fractal geometry, complexity, and network theories provides a context for understanding and building algorithms that can describe the complex nature of the flow of information in real networks such as the Web.

4.1.2  The Internet

The Internet is a network of physical connections between computers and other telecommunication devices. The topology of the Internet is studied from two different perspectives. On the router level, the nodes are routers and the edges are the physical connections between them. On the interdomain (or autonomic system) level, each domain comprising hundreds of routers and computers is represented by only one node, and an edge connects two domains if there is at least one route connecting them. The Internet was studied considering both levels (Ravasz and Barabási 2003), and, in every case, the conclusion was that the degree distribution respects a power law. The Internet as a network also manifests phenomena like clustering and small path length (Lan and Heidemann 2003).

In the first models proposed for the simulation of traffic in large communication networks, only Poisson or renewal processes were considered. In either case, arrivals were memoryless in the Poisson case, or memoryless at renewal points, and interarrival intervals were exponentially distributed. The Poisson arrival model and exponentially distributed holding time model allowed analytically and computationally simple Markov chains to be used for modeling. A large number of works have focused on modeling Internet topologies and on developing realistic topology generators. Waxman (1988) introduced the first topology generator that became widely known. The Waxman generator was based on the classical Erdös–Rényi random graph model. After it became evident that observed networks have little in common with classical random graphs, new generators tried to mimic the perceived hierarchical network structure and were consequently called structural. Then Faloutsos et al. (1999) discovered that the degree distributions of router-level topologies of the Internet followed a power law. Structural generators failed to reproduce the observed power laws. This failure led to a number of subsequent works trying to resolve the problem.

The existing topology models capable of reproducing power laws can be roughly divided into the following two classes: causality-aware and causality-oblivious (Dimitropoulos et al. 2009). The first class includes the Barabási–Albert (BA) model, the highly optimized tolerance (HOT) model (Casal et al. 1999) and their derivatives. The models in this class employ preferential attachment mechanisms to generate synthetic Internet topologies and incremental growth of the network by adding nodes one by one and links to a graph based on a formalized network evolution process. One can show that both BA and HOT growth mechanisms produce power laws. On the other hand, the causality-oblivious approaches try to match a given (power-law) degree distribution without accounting for different forces that might have driven the evolution of a network to its currently observed state. The models in this class include random graphs with the given expected degree sequences (Chung and Lu 2002) and Markov graph rewiring models (Maslov et al. 2004). However, Internet traffic behaves very differently from such simple Markovian models. Traffic measurements made at the local area networks (LAN) and wide area networks (WAN) suggest that traffic exhibits variability (traditionally called “burstiness”) over multiple time scales. The second-order properties of the counting process of the observed traffic displayed behavior that is associated with self-similarity, multifractals, and/or long-range dependence (LRD). This indicates that there is a certain level of dependence in the arrival process. Near-range and long-range dependencies often manifest themselves in a network by causing frequent and irremediable packet losses and other serious effects in the network.

Dependencies and burstiness in traffic hence brought in an enormous amount of attention from researchers. They attempted to develop mathematically based models that would help explain the nature of the systems exhibiting such phenomena and provide critical insight into the actual mechanisms that led to this behavior. Models like fractional Brownian motion and chaotic maps were suited to capture the second-order self-similar behavior of traffic. Their results were difficult to get and harder to apply, and such models did not provide insight into the actual mechanism of traffic generation. A simpler, more accurate, and analytically tractable model that provides more physical insight into why they are meaningful on physical grounds would help the network designers produce more effective and efficient designs.

The Internet is a prime example of a self-organizing complex system, having grown mostly in the absence of centralized control or direction. In this network, information is transferred in the form of packets from the sender to the receiver via routers, computers that are specialized to transfer packets to another router “closer” to the receiver. A router decides the route of the packet using only local information obtained from its interaction with neighboring routers, not by following instructions from a centralized server. A router stores packets in its finite queue and processes them sequentially. However, if the queue overflows due to excess demand, the router will discard incoming packets, a situation corresponding to congestion. A number of studies have probed the topology of the Internet and its implications for traffic dynamics.

To efficiently control and route the traffic on an exponentially expanding Internet, one must not only capture the structure of current Internet, but allow for long-term network design. After the already mentioned discovery of Faloutsos, according to which Internet is a scale-free network with a power-law degree distribution, several contributors found that the Internet flow is strongly localized: most of the traffic takes place on a spanning network connecting a small number of routers that can be classified either as “active centers,” which are gathering information, or “databases,” which provide information. Experimental evidence for self-similarity in various types of data network traffic is already overwhelming and continues to grow. So far, simulations and analytical studies have shown that it may have a considerable impact on network performance that could not be predicted by the traditional short-range-dependent models. The most serious consequence of self-similar traffic concerns the size of bursts. Within a wide range of time scales, the burst size is unpredictable, at least with traditional modeling methods.

This is the point from which the authors of this book assume that the traffic behavior is strongly influenced and depends on the network free-scale structure and that the self-similarity confers a fractal aspect for both traffic and topology.

4.2  Main approaches on networks topology modeling

4.2.1  Random graph theory

The random graph theory was proposed by Erdös and Rényi (1960), after Erdös had discovered the usefulness of stochastic methods when studying graph theory problems. A thorough analysis on this topic is given in the classic book of Bollobas (Bollobas 1985) complemented by the historical guide of the Erdös–Rényi approach of Karonski and Rucinski (1997). Following this publication, the most important results of random graph theory are provided, by highlighting the aspects relevant to complex networks. In their first article about random graphs, the Erdös–Rényi model is defined as a set of N nodes connected by n edges chosen randomly from the (N (N–1))/2 possible edges. There are a total of $C_{\left(N\left(N-1\right)\right)/2}^n$ graphs with N nodes and n edges, which produce a probability space in which every realization is equally probable.

The random graph theory studies the probability space properties for graphs with N nodes when N → ∞. Many random graph properties can be determined using probabilistic arguments. In this matter, Erdös and Rényi used a definition such that almost every graph has a Q property if the probability of having Q approaches tends to 1 for N → ∞. Among the problems addressed by Erdös and Rényi are some in direct connection with understanding complex networks.

In mathematics, the construction of a random graph is often called evolution: starting from a set of N isolated vertices, the graph evolves by adding random edges. The graph obtained at different levels during this process corresponds to increasingly higher p connection probabilities, and obtaining in the end a completely connected graph (having a maximum number of edges n = N(N − 1)/2) for p → 1. The main goal of the random graph theory is to determine the p connection probability for that a certain graph property appears. The greatest discovery of Erdös and Rényi is that many important random graph properties appear quite abruptly. Thus, for a given probability, almost every graph has a property Q (e.g., every pair of nodes is connected through a set of consecutive edges) or, on the contrary, almost no graph has it. The transition from highly improbable to highly probable for a certain property is usually quick. Thus, for random graph theory, the probability of occupation is defined as a function of the system dimension: p represents the fraction of existing edges from the total of N(N − 1)/2 possibilities. Larger graphs with the same p will contain more edges, and thus properties like cycles may appear for smaller values of p more easily in larger graphs than in smaller ones. This means that for many properties Q in random graphs, there is no single threshold N that is independent, but rather a threshold function must be defined depending on the system dimension and p_c(N → ∞) → 0. Also, it can be observed that the average graph degrees

$<k>=2n/N=p\left(N-1\right)\cong pN$

(4.2)

has a critical value that is independent on the system dimension.

The component of a graph is by definition a connected, isolated subgraph, known also as a cluster in network research and percolation theory. As it was pointed out by Erdös and Rényi, there is an abrupt change in the cluster structure of a random graph when 〈k〉 tends to 1.

If 0 < 〈k〉 < 1, almost every cluster is either a tree either it contains exactly one cycle. Although cycles are present, almost all nodes belong to trees. The average number of clusters is of the order N − n, where n is the number of edges, meaning that by adding on this scale a new edge, the number of clusters decreases by one. The largest cluster is a tree and its dimension is proportional to ln N.

In a random graph with p connection probability, the k_i degree of one node i follows a binomial distribution with N − 1 and p parameters

$P(k_i=k)=C_{N-1}^k{p}^k{\left(1-p\right)}^{N-1-k}$

(4.3)

This probability represents the number of ways in which k edges can be drawn starting from a certain node: the probability of k edges is p^k, the probability of no additional edges is (1 − p)^N−1−k, and there are C_N-1^k equivalent ways to select the k starting points for these edges. Moreover, if i and j are distinct nodes, then P(k_i = k) and P(k_j = k) tend to be independent random variables. To determine the distribution of the graph degree, the number of k degree nodes, X_k, must be studied. The main goal is to determine the probability for X_k to take a given value, P(X_k = r).

According to Equation 4.3, the expected value for the number of nodes with k degree is

$E(X_k)=NP(k_i=k)={\text{λ}}_k$

(4.4)

where

${\text{λ}}_k=N{C}_{N-1}^k{p}^k{\left(1-p\right)}^{N-1-k}$

(4.5)

The diameter of a graph is defined as the maximum distance between any two nodes. Strictly speaking, the diameter of an unconnected graph (i.e., containing only isolated clusters) is infinite, but it can be defined as the maximum diameter of its clusters. Random graphs tend to have small diameters when p is not too small. When 〈k〉^l is equal to N the diameter is proportional to ln(N)/ln(〈k〉), thus it depends only logarithmically on the number of nodes (Albert and Barabási 2002). This means that when considering all graphs with N nodes and p connection probability, the value scale through which the diameters of these graphs can vary is very small, concentrated around

$d=\frac{\ln \left(N\right)}{\ln \left(pN\right)}=\frac{\ln \left(N\right)}{\ln \left(\langle k\rangle \right)}$

(4.6)

Let finally define the clustering coefficient of a complex network. If in a random graph, a node and its neighbors are considered, the probability for two of these neighbors to be connected is equal to the probability for two randomly chosen graphs to be connected. As a result, the clustering coefficient of a random graph is

$C_{\text{rand}}=p=\frac{\langle k\rangle }{N}$

(4.7)

The ratio between the clustering coefficient and the average degree of real networks is a function of dimension (Barabási et al. 2003).

4.2.2  Small-world networks

Experiments show that real networks have the small-world property just like random graphs, but they have unusually large clustering coefficients. Moreover, the clustering coefficient seems to be independent of the network size. This last property is characteristic of the ordered lattices, whose clustering coefficients are independent of the dimension and depend strictly on the coordination number. Such small size regular lattices, however, do not have small trajectories: for an n-dimensional hyper cubic lattice the average node to node distance is scaled with N^1/d, and increases with N faster than the logarithmic increase noticed for the real and random graphs. The first successful attempt to generate graphs having large clustering coefficients and small trajectory length ℓ are owed to Watts and Strogatz (1998), which proposed a model with a single parameter that interpolates between a finite-dimensional lattice and a random graph.

In order to understand the coexistence of small trajectory lengths and clustering, the behavior of the clustering coefficient C(p) and the average trajectory length ℓ(p) will be studied as a function of the reconnection probability p. For a circular lattice ℓ(0) ≅ N/2K ≫ 1 and C(0) ≅ 3/4, so that ℓ is linearly scaled with the system dimension, and the clustering coefficient is large. Additionally, for p → 1 the model converges to a random graph for that ℓ(1) ~ ln(N)/ln(K) and C(1) ~ K/N, so that ℓ scales logarithmically with N, and the clustering coefficient decreases with N. These limit cases may suggest that a large C coefficient is always associated with a large ℓ, while a small C with a small ℓ. Contrarily, Watts and Strogatz discovered that a large interval of p exists in which ℓ(p) tends to ℓ(1) and C(p) ≫ C(1). The regime starts with a quick drop of ℓ(p) for small values of p, while C(p) remains constant, thus producing networks that are grouped, but have a small characteristic trajectory length. This coexistence of small ℓ and large C values manifests an excellent resemblance to the real networks characteristics, determining many researchers to name such systems small-world networks. In the following, the main result regarding the properties of small-world models will be presented in brief.

4.2.2.1  Average trajectory length

As previously stated, in the WS model there is a change in scaling the characteristic trajectory length ℓ with the increase of the fraction p for the reconnection of edges. For smaller values of p, ℓ is scaled linearly with the system dimension, while for a large p, the scaling is logarithmic. The origin for the rapid drop of ℓ is the appearance of shortcuts between nodes. Every shortcut, randomly created, is probable to connect separate parts at long distances in the graph, and thus, have a significant impact on the characteristic trajectory length of the entire graph. Even a small fraction of the shortcuts is enough to drastically decrease the average trajectory length, while on a local level the network remains very ordered. Watts demonstrated that ℓ does not start to decrease until p ≥ 2/NK, thus guaranteeing the existence of at least one shortcut. This implies that the transition p depends on the system dimension, or, on the contrary, there is a crossover length p dependent on N* so that if N < N* then ℓ ~ N, but if N > N* then ℓ ~ ln(N). Today, it is widely accepted that the characteristic trajectory length follows the general scaling form

$\mathcal{l}\left(N,p\right)~\frac{N}{K}f\left(pK{N}^d\right)$

(4.8)

where f(u) is an universal scaling function that satisfies

$f\left(u\right)=\{\begin{array}{cc}\text{constant}& \text{if\hspace{0.17em}}u\ll 1\\ \ln (u)/u& \text{if\hspace{0.17em}}u\gg 1\end{array}$

(4.9)

Several attempts have been made to calculate the exact distribution of the trajectory length and the average trajectory length ℓ. Dorogovtsev and Mendes (2002) have studied a simpler model that contained a circular lattice with oriented edges of length ℓ and a central node connected with the probability p to the nodes of the lattice through nonoriented edges of length 0.5. They calculated precisely the distribution of the trajectory length through this model, showing that ℓ/N depends only on the scaling variable pN, and the functional shape of this dependence is similar to ℓ(p) obtained numerically in the WS model.

4.2.2.2  Clustering coefficient

Besides the small average trajectory length, the small-world networks have a relative large clustering coefficient. The WS model manifests this duality for a wide range of the reconnection probability p. In a regular lattice (p = 0), the clustering coefficient does not depend on the lattice size but only on its topology. While the edges of the lattice are randomly reconnected, the clustering coefficient remains close to C(0) until larger values for p. According to this, C′(p) is the ratio of the average number of edges between the neighbors of a node to the average number of possible edges between those neighbors.

4.2.2.3  Degree of distribution

In the WS model, for p = 0, every node has the same degree K, so that the degree distribution is a delta function centered around K. A nonnull p introduces disorder in the network, widening the degree distribution but still keeping the average degree K. Because only one end of each edge is reconnected (a total of pNK/2 edges), each node has at least K/2 edges after the reconnection process. As a consequence, for K > 2, there are no isolated nodes, and the network is normally connected for a wide range of connection probabilities, unlike a random graph formed of isolated groups.

4.2.2.4  Spectral properties

The spectral density ρ(λ) of a graph highlights important information about its topology. To be specific, it was observed that for large random graphs ρ(λ) converges to a semicircle. Thus, it comes as no surprise that the spectrum of the WS model depends on the reconnection probability p. For p = 0, the network is regular and periodic, so that ρ(λ) contains numerous singularities. For intermediate values of p these singularities ρ(λ) retains a strong inclination. Finally, when p → 1, then ρ(λ) tends to the semicircle law that describes random graphs. Thus, the e high regularity of small-world models for a variety of values for p is highlighted by the results regarding the spectral properties of the Laplace operator, which provides information about the time evolution of a diffuse graph field.

4.2.3  The scale-free (SF) model

Empirical results demonstrate that many large networks are scale-free, meaning that the degree of distribution follows a power law for large values of k. Moreover, even for those networks for that P(k) has an exponential tail, the degree of distribution deviates from the Poisson distribution (Li et al. 2005). It was seen in Sections 4.2.1 and 4.2.2 that the random graph theory and the WS model cannot reproduce this characteristic. While random graphs can be directly constructed to have degree distributions of power law type, they can only postpone an important question: what is the mechanism responsible for generating scale-free networks? In this section, it will be shown that in order to answer this question a deviation from topology modeling to constitution and evolution of the network is necessary. At this point, the two approaches do not appear to be distinct, but it will become clear that a fundamental difference exists between random graph and small-world modeling, and the modeling of power law graphs. While the purpose of the previous models was to build a graph with correct topological characteristics, the modeling of scale-free networks will focus on capturing the dynamics of the network. Thus, the main assumption behind evolutionary or dynamic networks is that if the processes that assembled the present networks are correctly captured, then their topology can also be obtained.

4.2.3.1  Definition of the scale-free network (SFN) model

The origin of the power law degree distribution in networks was first addressed by Albert and Barabási (2002), who argued that the free-scale nature of real networks starts from two generic mechanisms common to many real networks. The network models discussed so far imply starting from a fixed number of vertices N, which are afterward connected or reconnected randomly, without altering N. By contrast, the majority of real networks describe open systems that grow during their life span by further adding new nodes. For example, the WWW network grows exponentially over time by adding new Web pages, or the research literature grows constantly by the publishing of new documents.

Additionally, the network models discussed until now assume that the probability for two nodes to be connected (or their connections to be modified) is independent of the node degree, meaning that the new edges are placed randomly. The majority of the real networks display a preferential attachment, and thus the connection probability of one node depends on its degree. For example, a Web page will rather include links to popular documents with an already large degree, because this kind of documents are easy to find and well known; a new manuscript is more likely to cite a well-known publication and so a largely cited one, than the less cited and less known ones.

These two ingredients, growth and preferential attachment, inspired the introduction of the scale-free model (SF) that has a power law degree distribution. The SF model algorithm is

1.  Growth: starting from a small number m₀ of nodes, at each step, a new node is added with m(≤m₀) edges that link the new node to m different already existing ones.

2.  Preferential attachment: When node to which the new node will link to are chosen, the probability ∏ that the new node to be connected to node i depends on the degree k_i of node i, so that

${\displaystyle \prod \left(k_i\right)=\frac{k_i}{{\displaystyle {\sum }_j{k}_j}}}$

(4.10)

After t steps this algorithm generates a network with N = t + m₀ nodes and mt edges.

4.2.3.2  General SFN properties

Barabási and Albert suggested that scale-free networks emerge in the context of growing network in which new nodes connect preferentially to the most connected nodes already in the network. Specifically,

Figure 4.1 A scale-free network graph.

$p_i\left(n+1\right)=\frac{k_i\left(n\right)}{{\displaystyle \sum _{1-n_0}^n{k}_i\left(n\right)}}$

(4.11)

where n is the time and number of nodes added to the network, n₀ is the number of initial nodes in the network at time zero, k_i is the degree of node i and p_i(n + 1) is the probability of a new node, added at time n + 1 linking to node i.

As illustrated in Figure 4.1, as time ticks by, the degree distribution of the nodes becomes more and more heterogeneous since the nodes with higher degree are the most likely to be the ones new nodes link to. Significantly, scale-free networks provide extremely efficient communication and navigability as one can easily reach any other node in the network by sending information through the “hubs,” the highly connected nodes. The efficiency of the scale-free topology and the existence of a simple mechanism, leading to the emergence of this topology led many researchers to believe in the complete ubiquity of scale-free network. Note that scale-free networks are a subset of all small-world networks because (i) the mean distance between the nodes in the network increases extremely slowly with the size of the network and (ii) the clustering coefficient is larger than for random networks.

4.2.3.3  Diameter of scale-free networks

It was shown that scale-free networks with degree exponent 2 < λ < 3 possess a diameter D ~ ln N, smaller even than that of random and small-world networks (Dorogovtsev and Mendes 2001). If the network is fragmented, we will only be interested in the diameter of the largest cluster (assuming there is one). In this study, we consider the diameter of a scale-free network defined as the average distance between any two sites on the graph. Actually, it easier still to focus on the radius of a graph, L ≡ 〈l〉 as the average distance of all sites from the site of highest degree in the network. The diameter of the graph D is restricted to L ≤ D ≤ 2L and thus scales like L.

4.2.3.4  Average trajectory length

The average trajectory length is smaller in SFNs than in random graphs for every N, thus indicating that the heterogeneous scale-free topology is more efficient in closing in the nodes than the homogeneous topology of random graphs. Note that average trajectory length in the SF model increases almost logarithmically with N. One can observe that the prediction of Equation 4.6, although gives a good approximation for the random graph, systematically underestimates the average trajectory length of the SF network, and also the average trajectory length of real networks.

4.2.3.5  Node degree correlation

In the random graph models with random average degree distributions, the node degrees are not correlated. Krapivsky and Redner demonstrated that for SF models, the correlations develop spontaneous between the degrees of already connected nodes (Krapivsky and Redner 2001). It is considered that all the pair of nodes with degree k and l are connect by an edge. Without losing generality, it can be assumed that the node with degree k was added later to the system, implying from that moment on that k < l, such that older nodes have a higher degree than the newer ones, and, for simplicity, m = 1 is used.

4.2.3.6  Clustering coefficient

Even if the clustering coefficient has been previously studied for the WS model, there is no analytical prediction for the SF model. It was discovered that the clustering coefficient of a scale-free network is almost five times larger than the one of a random graph, and this factor increases slightly with the number of nodes. Nevertheless, the clustering coefficient of the SF model decreases with the network dimension following approximately the power law C ~ N^−0.75, which, although being a slower decrease than C = 〈k〉 N⁻¹ noted for random graphs, it is still different from the small-world behavior, where C is independent of N.

4.3  Internet traffic simulation with scale-free network models

4.3.1  Choosing a model

To model a distributed network environment like the Internet, it is necessary to integrate data collected from multiple points in a network in order to get a complete picture of network-wide view of the traffic. Knowledge of dynamic characteristics is essential to network management (e.g., detection of failures/congestion, provisioning, and traffic engineering like QoS routing or server selections). However, because of a huge scale and access rights, it is expensive (sometime impossible) to measure such characteristics directly. To solve this, methods and tools for inferencing of unobservable network performance characteristics are used in large-scale networking environment. A model where inference based on self-similarity and fractal behavior can be applied is the scale-free network (SFN) model.

The simulation of scale-free networks is necessary in order to study their characteristics like fault-tolerance and resistance to random attacks. However, large-scale networks are difficult to simulate due to the hefty requirements imposed on CPU and memory. Thus, a distributed approach to simulation can be useful, particularly for large-scale network simulations, where a single processor is not enough.

From the different variants that have been suggested for the SFN model, one of them known as the “Molloy–Reed construction” (Molloy and Reed 1998) will be considered in the following. This model ignores the evolution and assumes only the degree of distribution and no correlations between nodes. Thus, the site reached by following a link is independent of the origin. This means that a new node will more probably attach to those nodes that are already very well connected, that is, they have a large number of connections with other nodes from the network. Poor connected nodes, on the other hand, have smaller chances of getting new connections (see Figure 4.2.).

Besides following the repartition law mentioned above, some other restrictions (for example, those related to cycles and long chains) had to be applied in order to make the generated model more realistic and similar to the Internet. Another obvious restriction is the lack of isolated components (see Figure 4.3).

A more subtle restriction is related to the time-to-living (TTL), which is a way to avoid routing loops in a real Internet. This translates in a restriction for our topology—there can be no more than 30 nodes to get from any node to any other node. Another subtle restriction is that the generated network will also have redundant paths, that is, multiple possible routes between nodes. In other words, the Internet model topology should not “look” like a tree, but should rather have numerous cycles.

The algorithm used for the generation of the scale-free network topology is generating networks with a cyclical degree that can be controlled, in our case, approximately 4% of the added nodes form a cycle. One more restriction is that we try to avoid long-line type of scale-free networks—a succession of several interconnected nodes—structure that does not have a real-life Internet equivalent, so our algorithm makes sure such a model is not generated.

Figure 4.2 Graphic representation of the generated network for 200 network nodes and λ = 2.35.

Figure 4.3 Graphic representation of the generated network for 200 network nodes and λ = 2.85.

4.3.2  Proposed Internet model

The generated topology consists of three types of nodes: routers, servers, and customers.

Routers are defined as nodes with one or several links that do not initiate traffic and do not accept connections. Routers can be one of the following types: routers that connect primarily customers, routers that connect primarily servers and routers that connect primarily other routers. Routers that connect primarily customers have hundreds or thousands of type one connections (leaf nodes) and a reduced number of connections to other routers. Routers that connect primarily servers have a reduced number of connections to servers in the order of tenths and reduced number (2 or 3) connections to other routers. Routers that connect primarily routers have a number in the order of tenths of connections to other routers and do not have connections to neither servers nor customers.

Servers are defined as nodes with one connection but sometimes could have two or even three connections. Servers only accept traffic connections but do not initiate traffic.

Customers (end-users) are defined as nodes that have only one connection, very seldom two connections. Customers initiate traffic connections toward servers at random moments but usually in a time succession. For our proposed model, we chose a 20:80 customer-to-server ratio.

4.3.2.1  Scale-free network design algorithm

We designed and implemented an algorithm that generates those subsets of the scale-free networks that are close to a real computer network such as the Internet. Our application is able to handle very large collections of nodes, to control the generation of network cycles, and the number of isolated nodes. The application was written in Python being, as such, portable. It runs very fast on a decent machine (less than 5 min for 100.000 nodes model).

Network generation algorithm:

1.  Set node_count and λ

2.  Compute the optimal number of nodes per degree

3.  Create manually a small network of three nodes

4.  For each node from four to node_count

a.  Call add_node procedure

b.  While adding was not successful

c.  Call recompute procedure

d.  Call add_node procedure

5.  Save network description file

add_node procedure

1.  According to the preferential attachment, compute the degree of the parent node

2.  If degree could be chosen then exit procedure

3.  Compute the number of links that the new node shall establish with descendants of its future parent, according to copy model

4.  Chose randomly a parent from the nodes having the degree as computed above

5.  Compute the descendant_list, the list of descendants of the newly chosen parent

6.  Create the new node and links

7.  For each descendant of the descendant_list and create the corresponding links

8.  Exit procedure with success code

recompute procedure

1.  For each degree category

a.  Calculate the factor needed to increase the optimal count of nodes per degree

b.  If necessary increase the optimal number of nodes per degree

2.  Exit procedure

The algorithm starts with a manually created network of several nodes, and then using preferential attachment and growth algorithms, new nodes are added. We introduced an original component, the computation in advance of the number of nodes on each degree level. The preferential attachment rule is followed by obeying to the restriction of having the optimal number of nodes per degree.

We noticed that the power law is difficult to follow while the network size is growing, as a result we calculate again the optimal number of nodes per degree level at given points in the algorithm. This is necessary because the bigger the network the higher the chance that a new node will be attached only to some specific very-connected nodes. In a real network, such as the Internet this will not happen. If only the preferential and growth algorithms are followed, then the graph will have no cycles, which is not realistic, therefore we introduced a component from the “copy model” for graph generation in order to make the network graph include cyclical components. This component ensures that each new node is also attached to some of its parent-node descendants using a calibration method. The calibration method computes the number of additional links that a new node must have with the descendants of its parent. This number depends on how well-connected is the parent and it also includes a random component.

Figure 4.4 Graphic representation of the distribution law for a scale-free network model and for a randomized network with 10,000 nodes.

The output of the application is a network description file that can be used by several tools like, for instance, a tool to display the power law. This file is stored using a special format needed in order to reduce the amount of disk writes.

In Figure 4.4, we compare an almost random network distribution law and a free-scale distribution law. On the ϒ-axis, we represent the number of connections and on the X-axis, the number of nodes having this number of connections. It was impossible to obtain a completely random network given the limitations imposed by the Internet model, so further only the scale-free network model will be discussed.

4.3.2.2  Traffic generation

Traffic generation is an essential part of the simulation as such, and we decided to initiate randomly between 1 and 3 simultaneous traffic connections from “customer” nodes and for the sake of simplicity, we used ftp sessions to randomly chosen destination servers. We also decided that the links connecting routers should have higher speeds than lines connecting customers to routers, for example—server-router 1 Gbps, client-router 10 Mbps, router-router 10, 100 Mbps or 1 Gbps depending on the type of router. The code generated respecting these two conditions is added to the network description file, being ready to be processed by the simulator.

4.3.2.3  Single-CPU simulation

We used a modular approach that allows us to later reuse components for different parts of the simulation. For example, the same network model generated by the initial script can be used for both single-CPU and distributed simulations, allowing a comparison between the two types of simulation. Standalone simulations were run under University of California Berkeley’s NS2 network simulator. NS2 (The Network Simulator) (Chung 2011). We noticed that on a single machine, as network size increases, very soon we hit the limit of the network sizes that can be simulated due to resource limitations, mostly on memory, but also high CPU load. In case of small size network models, such as with a few nodes, simulations can be run on a single machine. The results provided by NS2 were visualized using the nam (network animator) software package. The topology generator gives different colors to different type of nodes: server, client, and router. Details about the networking traffic through each network node are parsed from the simulator output.

4.3.2.4  Multi-CPU simulations

Unfortunately NS was not designed to run on parallel machines. The main obstacle in running NS in a distributed or parallel environment is related to the description of objects in the simulation. As such, we ran our distributed simulations under Georgia Tech’s extension to NS2, pdns [PDNS], which uses a syntax close to that of NS2, the main differences being a number of extensions needed for the parallelization so that different instances of pdns can communicate with each other and create the global image of the network to be simulated. Each simulator running on different nodes needs to know the status of other simulators. Furthermore, if we try to split the network description file into separate files and run each of these in separate simulation contexts, we need to find a way to communicate parameters between the simulation nodes. All simulations are running 40 s of simulated traffic scenarios.

4.3.2.5  Cluster description

In order to create a parallel or distributed environment, we have built a cluster using commodity hardware and running Linux as operating system (Mocanu and Ţarălungă 2007). The cluster can run applications using a parallelization environment. We have written and tested applications using parallel virtual machine (PVM), which is a framework consisting of a number of software packages that accomplish the task of creating a single machine that spans across multiple CPUs, by using the network interconnection and a specific library (Grama et al. 2003). Our cluster consists of a “head” machine and a number of six cluster nodes. The “head” provides all services for the cluster nodes—IP allocation, booting services, file system (NFS) for storage of data, facilities for updating, and managing and controlling the images used by the cluster nodes as well as access to the cluster. The “head” computer provides an image for the operating system that is loaded by each of the cluster nodes since the cluster nodes do not have their own storage media. The application partition is mounted read-only while the partition where data is stored is mounted read-write and accessible to the users on all machines in a similar manner providing transparent access to user data. In order to access the cluster, users must connect to a virtual server located on a head machine. This virtual server can also act as a node in the cluster when extra computation power is needed.

4.3.2.6  Network splitting

In order to use PDNS simulation, we needed to split the network into several quasi-independent subnetworks. Each instance of PDNS handles a specific subnetwork, thus the dependencies between them need to be minimal, that is, there shall be as few as possible links between nodes located in different subnetworks. In order to have a federated simulation approach, we designed and implemented a federalization algorithm in order to split the original generated network into several small ones. The algorithm that generates n federative components chooses the most n linked nodes, assigned them to an empty federation and starts a procedure similar to the breadth-first search algorithm. Each node is marked as being owned by a federation. The pdns script generator takes as input the generated network description and the generated federations, respectively. Depending on the connectivity of nodes, they are assigned the role of routers, servers, end-users, and the corresponding traffic scenario is associated with them.

4.3.3  Simulation results and discussion

We have decided to run simulations for 40 s of traffic for a scale-free network model with 10000 nodes. At such a scale, a one-node processing is impossible because the cluster node runs out of memory. Still, to get valid results, we had run the simulation on a much more powerful machine with plenty of memory and virtual memory. We chose two different scenarios, one with a moderate network traffic and another scenario with a heavy network traffic. Each scenario was simulated five times under similar load conditions, using two to six CPUs and we noted the time used for the actual simulation (in seconds). The results are presented in Tables 4.1 and 4.2.

For the first scenario, we noted that there is a point where adding more nodes in the simulation does not help but rather increases the simulation time. In this scenario, the optimum number of nodes is 5.

Table 4.1 Scale-free network model with 10,000 nodes and moderate network traffic (40 seconds)

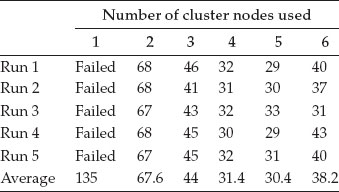
Table 4.2 Scale-free network model with 10,000 nodes and heavy network traffic (40 seconds)

The second scenario requires much more resources as can be seen from the single-processor simulation, which again failed on the cluster nodes but was successful on a more powerful machine, although it takes a longer time. Also in this simulation, we see that adding more nodes (in our case more than 4), the simulation process is slower.

One can observe that the 2-CPU simulation is actually faster than the 3-CPU simulation, although the optimal number of nodes is not 2. Running pdns is more efficient than running NS2 especially on large-size network models where sometimes pdns is the only solution. However, there are limitations in the number of cluster nodes that could process a given network model since more nodes are used, more traffic links between different cluster nodes are to be simulated and therefore more time is spent on interprocessor communication. Anyway, it is very important to split the network model correctly into smaller subnetworks (federations) since there is a tradeoff between the degree of separation and federation balancing—the more separated the subnetworks are, the more unbalanced they become.

4.4  Improvement of Internet traffic QoS performance

4.4.1  Quality of service (QoS) requirements in high-speed networks

The new broadband high-speed networks are designed to integrate a wide range of audio, video and data traffic within the same network. In these networks, the stringent quality of service (QoS) requirements of real-time multimedia applications are met by the mean of special services providing guarantees. One distinguishes between two main kinds of such services: deterministic and statistical (Chao and Guo 2001). The deterministic service, also called guaranteed service within the Internet framework, is aimed to provide strict guarantees on the QoS requirements. The mathematical basis of the deterministic service is a network calculus that allows obtaining deterministic bounds on delay and buffering requirements in a communication network. This model provides bounds only on the maximal delay that traffic can undergo through the different elements in the network. The statistical service is intended to provide only statistical (probabilistic) guarantees. For services offering statistical guarantees, one is rather interested in bounding the mean delay or the probability that the delay exceeds a certain value. The main advantage of the statistical service over the deterministic service is that it can achieve higher network utilization, at the expense of some minor quality degradation.

Two notable models of statistical services are used to meet the demand for QoS: integrated services (IntServ) and differentiated services (DiffServ). The IntServ model is characterized by resource reservation; before data is transmitted, applications must set up paths and reserve resources along the path. IntServ aims to support applications with different levels of QoS within the TCP/IP (transport control protocol/Internet protocol) architecture. IntServ, however, requires the core routers to remember the state of a large number of connections, giving rise to scalability issues in the core of the network. It is therefore suitable at the edge network where the number of connections is limited. The DiffServ model is currently being standardized to provide service guarantees to aggregate traffic instead of individual connections. The model does not require significant changes to the existing Internet infrastructure or protocol. DiffServ does not suffer from scalability issues, and hence is suitable at the core of the network. It is therefore believed that a significant part of the next generation high-speed networks will consist of IntServ at the edge and DiffServ at the core of the network.

Unfortunately, all of these algorithms have poor burst loss performances, even at low traffic loads, because the real traffic is bursty. To solve this problem, we discuss in the following a novel burst assembly algorithm with traffic-smoothing functions (the traffic is smoothed by restricting the burst length to a threshold). Compared with existing algorithms, our scheme can improve network performance in terms of the burst loss ratio. The simulation results show that our proposed scheme can lighten burst loss ratio for TCP flows of a high-speed network.

4.4.2  Technologies for high-speed networks

In high-speed networks, all communications are limited by the electronic processing capabilities of the system. Although hardware-based high-speed electronic IP routers with capacity up to a few hundred gigabits per second are available now, there is still a serious mismatch between the transmission capacity of wavelength division multiplexing (WDM) optical fibers and the switching capacity of electronic IP routers. With IP traffic as the dominant traffic in the networks, the traditional layered network architecture is no longer adapted to the evolution of the Internet. In the multilayered architecture, each layer may limit the scalability of the entire network, as well as adding the cost of the entire network. As the capabilities of both routers and optical cross-connects (OXCs) grow rapidly, the high data rates of optical transport suggest bypassing the SONET/SDH and ATM layers and moving their necessary functions to other layers. This results in a simpler, more cost-efficient network that can transport very large volumes of traffic. On the other hand, the processing of IP packets in the optical domain is still not practical yet, and the optical router control system is implemented electronically. To realize an IP-over-DWDM architecture, several approaches, such as wavelength routing (WR) (Zang et al. 2004), optical packet switching (OPS) (O’Mahony et al. 2001), and optical burst switching (OBS) (Xiong et al. 2004), have been proposed. Of all these approaches, optical burst switching (OBS) can achieve a good balance between the coarse-gained wavelength routing and fine-gained optical packet switching, thereby combining others’ benefits while avoiding their shortcomings.

4.4.2.1  Characteristics of OBS networks

In an OBS network (shown in Figure 4.5), the edge routers and core routers connect with each other with WDM links. The edge nodes are responsible for assembling packets into bursts and deassembling bursts into packets. The core nodes are responsible for routing and scheduling based on the burst header packets.

The architecture of edge router aims to eliminate optical to electronic to optical (O/E/O) conversions and electronic processing loads, which are the bottlenecks of an OBS network. The ingress part of an edge node assembles multiple IP packets with the same egress address into a switching granularity called a burst. A burst consists of a burst header packet (BHP) and a data burst (DB). The BHP is delivered on a control channel; its corresponding DB is delivered on a data channel without waiting for a confirmation of a successful reservation. A channel may consist of one wavelength or a portion of a wavelength, in case of time-division or code-division multiplexing. When a BHP arrives at a core node, the core node converts it into an electronic signal, performs routing and configures the optical switching according to the information carried by the BHP. The DB remains in the optical domain without O/E/O conversion when it cuts through the core node.

Figure 4.5 OBS network model.

4.4.2.2  Burst assembly schemes

Burst assembly at the edge router is an important issue for OBS networks. Basically, there are two assembly schemes: threshold-based and timer-based. In a threshold-based scheme, a burst is created and sent into the optical network when the total size of the packets in the queue reaches a threshold value L_b. The shortcoming of the threshold-based scheme is that it does not provide any guarantee on the assembly delay that packets will experience. In a timer-based scheme, a timer is started at the initialization of the assembly. A burst containing all the packets in the buffer is generated when the timer reaches the burst assembly period T_b. A large timeout value T_b results in a large packet buffering delay at the edge node. On the other hand, a too small T_b results in too many small bursts and a high electronic processing load.

The choice of burst assembly algorithms depends on the type of traffic being transmitted. Timer-based algorithms are suitable for time-constrained traffic such as real-time applications because the upper bound of the burst assembly delay is limited. For a time-insensitive application such as file transmission, to reduce the overhead of control packets and increase OBS transmission efficiency, a threshold-based scheme may be more appropriate. Figure 4.6 shows the effect of load on timer-based and threshold-based assembly schemes.

Figure 4.6 Load effect in assembly schemes.

How to choose the appropriate time-out or threshold value for creating a burst is still an open issue. A smaller assembly granularity leads to a higher number of bursts and a higher number of contentions, but the average number of packets lost per contention is less. Also, it will increase the number of control packets. On the other hand, a higher assembly granularity will lead to a higher burst assembly delay and the average number of packets lost per contention is larger.

4.4.3  Traffic-smoothing using burst assembly schemes

4.4.3.1  Analysis of assembled traffic

A challenging issue in OBS is how to assemble IP packets into bursts at ingress nodes. As we assume there is no buffer in OBS networks, a burst loss event will occur if multiple bursts from different input ports are destined for the same output port at the same time. The burst arrival process is determined by the traffic characteristics such as the burst interarrival time and the burst length distributions, which are dependent on the burst assembly strategy. For the timer-based assembly algorithm, the burst size is unlimited when too many packets arrive suddenly. A larger burst is more likely to be blocked or to block other bursts during transmission. For the threshold-based and hybrid assembly algorithms, a large number of bursts will be generated and injected into the network in a short period when many packets arrive.

The network traffic characteristics have attracted considerable research attention because the traffic properties greatly influence the network’s performance. Let consider in a simple traffic model for a burst assembler {A(t),t > 0} be the cumulative amount of the input traffic in bits of the burst assembly function arriving during time interval (0, t], and {A^OBS(t), t > 0} be the cumulative amount of output traffic of the burst assembly function during time interval (0, t], that is, assembled traffic.

We define X_n(n ∈ N) as a sampled process of input traffic with the unit time of τ. Therefore, X_n = {A(nτ) − A((n − 1)τ), n ∈ N}. We assume X_n to be a wide-sense stationary discrete stochastic process, with constant mean μ = E[X_n]. Let S_n,m be the sum of m consecutive numbers from X_n; then $S_{n,m}\equiv {\displaystyle {\sum }_{j=\left(n-1\right)m}^{nm}{X}_j}$.

We define $X_n^{\left(m\right)}\equiv S_{n,m}/m$ and use the variance–time function $\text{Var}[X_n^{\left(m\right)}]=E[{(X_n^{\left(m\right)}-\text{μ})}^2]$ to represent the variance of input traffic. Here, $E[X_n^{\left(m\right)}]=E[X_n]=\text{μ}$.

Similarly, we also define ϒ_n(n ∈ N) as a sampled process of assembled traffic with the unit time interval of τ and assume it to be a wide-sense stationary discrete stochastic process. Here, ϒ_n = {A^OBS(nτ) − A^OBS((n − 1)τ), n ∈ N}. Then, the variance of assembled traffic can be measured by the variance–time function

$\text{Var[}{\Upsilon }_n^{\left(m\right)}]=E[{({\Upsilon }_n^{\left(m\right)}-{\text{μ}}^{\text{OBS}})}^2]$

(4.12)

where ${\Upsilon }_n^{\left(m\right)}$ is the mean value of m consecutive numbers from ϒ_n, and μ^OBS is the mean of ${\Upsilon }_n^{\left(m\right)}$ and can be expressed by $E[{\Upsilon }_n^{\left(m\right)}]=E[{\Upsilon }_n]={\text{μ}}^{\text{OBS}}$.

Here, we analyze the assembled traffic through a model based on fractional Brownian motion (FBM) proposed by the authors in a previous work (Dobrescu et al. 2004b). The FBM model is defined by

$A\left(t\right)=\text{λ}t+\sqrt{\text{λ}a}{Z}_H\left(t\right);T\in R$

(4.13)

where λ is the arrival rate for the packets, a is the variance of the coefficient for the arrival packet, and Z_H(t) is the normalized FBM with zero mean and variance of $\text{Var[}{Z}_H\left(t\right)]={\left|t\right|}^{2H}$, where H is the Hurst parameter and satisfies H ∈ [0:5; 1).

In our simulations, we have considered for large timescales (m > 200) that the variance–time curve is approximated using the FBM model for the parameter set λ = 564 Mb/s, a = 2.5 × 10⁶, and H = 0.85. In small timescales (m < 200), the traffic can be approximated by an FBM model with the parameter set = 564 Mb/s, a = 9 × 10⁵, and H = 0.75.

Since the variance of the aggregate of uncorrelated traffic will equal the sum of the individual source’s variance, we only have analyzed the variance of the assembled traffic of one burst source, using a timer-based burst assembly scheme. With a timer-based burst assembly algorithm, all packets in the assembly buffer will be sent out as a burst when the timer reaches the burst assembly period T_b. After a burst is generated, the burst is buffered at the edge node for an offset time before being transmitted to give its BHP enough time to reserve wavelengths along its route. During this offset time period, packets belonging to that queue will continue to arrive. Because the BHP that contains the burst length information has already been sent out, these arriving packets could not be included in the generated burst. When a burst is generated at one buffer, the future arriving packets will be stored at another buffer until the next assembly cycle. We assume that the interarrival time of the bursts from the same burst source is fixed as T_b. Accordingly, there will be no packets left in the assembly buffer at time $k{T}_{\text{b}}\left(k\in N\right)$. Therefore, $A^{\text{OBS}}k{T}_{\text{b}}=A\left(k{T}_{\text{b}}\right)$. We denote Q(t) as the number of bits that are buffered at the edge router. So $A^{\text{OBS}}\left(t\right)=A\left(t\right)-Q\left(t\right)$.

For the timer-based assembly algorithm, the Q(t) bits are at most the packets that arrive during [0, s], where s ∈ [0,T_b]. For simplification, we assume s is uniformly distributed in [0, T_b] and Q(s) is a Gaussian process with mean λ_s and variance λas^2H. We denote $\overline{E_Q}$ as the mean value of Q(t) observed at any sample point. Then, $\overline{E_Q}=\underset{T\to \infty }{\lim }\frac{1}{T}{\displaystyle {\int }_0^{T}Q\left(t\right)\text{d}t}$.

The difference between the original traffic and the assembled traffic can be denoted by

$\text{Δ}V\left(t\right)=\text{Var[}{A}^{\text{OBS}}\left(t\right)]-\text{Var[}A\left(t\right)]$

(4.14)

To describe the variance of assembled traffic A^OBS(t), the variance–time function becomes

$\text{Var}[{\Upsilon }_n^{\left(m\right)}]=E\left[\frac{A\left(m\text{τ}\right)}{m}\right]+\frac{1}{m^2}\text{Δ}V\left(m\text{τ}\right)$

(4.15)

From Equation 4.15, we can see there is an increase in the variance in short timescales. This indicates that the timer-based assembly algorithm will increase the variance of traffic. As the timescale increases, the difference between the original and assembled traffic becomes negligible because the traffic does not change significantly for large timescales.

4.4.3.2  Description of the proposed burst assembly algorithm

The simulation results on the discussed model show that the timer-based assembly algorithm could not reduce the variance of the real traffic, but do increase it in small timescales. Defining the traffic burstiness as the variance of the bit rate in small timescales, one can observe that a larger burstiness indicates that the traffic is burstier and more likely to exceed the capacity of the network and it results in burst loss events. So, a larger burstiness implies a higher burst loss ratio in bufferless OBS networks. One way to reduce the burst loss ratio is to control the burst sources at the edge nodes and thereby inject the bursts more smoothly into the network. This section discusses a novel burst assembly algorithm with traffic-smoothing functions, to reduce the burstiness of the assembled traffic.

A simple way to reduce the burstiness is a peak rate restriction. Conceptually, the number of bursts simultaneously arriving at an input port is most likely to reach a maximum value when the traffic is at a peak rate. Reducing the number of overlapping bursts on a link is for each ingress node to restrict the assembled traffic to a specified rate. In a timer-based assembly scheme, because the bursts are generated periodically, the traffic rate can be restricted by restricting the burst length to a threshold. Based on this idea, we propose a scheme, called adaptive timer-based, to reduce the burstiness of traffic.

For this scheme, we suppose each edge router has G queues to sort the arriving packets. Let the timer of queue Q[i] be denoted by T[i] and the length of Q[i] be denoted by L[i]. The threshold for generating a burst is L_th[i]. When the value of the queue length L[i] is smaller than L_th[i], all packets in Q[i] will be assembled into a burst. Otherwise, a burst is generated with the length of L_th[i] and the other packets are left in Q[i].

The scheme is thus implemented using the following algorithm:

•  Step 1. When a packet with a length of b arrives at Q[i], then if Q[i] is empty, start timer T[i], L[i] = b; else push packet into Q[i], with L[i] = L[i] + b.

•  Step 2. When T[i] = T_b if (L[i] > L_th[i]), L_b = L_th[i], L[i] = L[i] − L_th[i], T[i] = 0 and restart timer T[i]; else L_b = L[i], L[i] = 0, T[i] = 0 and stop timer T[i].

•  Step 3. Generate a burst with length L_b and send it into the OBS network.

Figure 4.7 shows a comparison of the timer-based (a) and adaptive timer-based (b) assembly algorithms. For the timer-based assembly algorithm, all packets in the assembly buffer will be multiplexed to a burst every assembly period. This makes for various burst sizes because the number of packets that arrive in each assembly period varies. On the other hand, the burst size in the adaptive timer-based assembly algorithm is restricted by the threshold L_th[i]. After an L_th[i] length of packets are assembled into a burst, the other packets will be left in the assembly queue for a future assembly process. So, the adaptive timer-based scheme can avoid a sudden increase in the burst size and makes the burst sent out more smooth than the timer-based assembly algorithm does.

Figure 4.7 Comparison of timer-based (a) and adaptive timer-based (b) algorithms.

Take into consideration the choice of L_th[i] to take advantage of the effects of the peak rate restriction. It is clear that the restriction of on the peak rate should be bigger than the average rate and the threshold L_th[i] must exceed the average burst length $\overline{L_M}\left(i\right)$, otherwise the traffic would be blocked at the edge nodes. As L_th[i] is close to $\overline{L_M}\left(i\right)\left(\text{α}\to 0\right)$, the transmission is almost the same as in a CBR transmission. However, this will result in enormous backlogs at the edge routers. The choice of α is a tradeoff between the effects of the peak rate restriction and the edge buffering delay. When too many packets suddenly arrive, if we still assemble packets into bursts using a small threshold L_th[i], the packets will suffer a large edge buffering delay.

4.4.4  Simulation results

To check the efficiency of our schemes, we have simulated a multiple hop network with a ring topology on a dedicated platform. We use OPNET as a simulation tool to study the performance of our schemes and compare them with existing dropping schemes, especially when the offset times are varied during transmission. The shortest-path-first routing method is used to establish a route between each pair of edge nodes E_i(i = 1 to 16), and the maximum hop distance is 10. Bursts are generated at each edge node E_i. We assume that the burst interarrival time follows an exponential distribution and the burst size follows a normal distribution. Note that these assumptions are the same as the ones in (Yu et al. 2002). Therefore, in our simulations, we have use the same ring topology and environment to test the performance of the integrated scheme when performing joint QoS with absolute constraints. The average burst size is 50 kbytes. All bursts are assumed to have the same initial offset time (the default value is 5 ms, which is small enough even for real-time applications). For a core node C_i(i = 1 to 16), we assume that each output link consists of 16 wavelengths with a transmission rate of 1 Gbps per wavelength. The basic processing time for BHP at each core node is set to be 0.1 ms. To investigate the service differentiation, we consider four classes, a load distribution of λ₁ = λ₂ = λ₃ = λ₄, and proportional parameters of s₁ = 1, s₂ = 2, s₃ = 4, and s₄ = 8.

For simplicity, in the simulations, the traffic load refers to the average traffic load on the links connecting two core nodes. Regarding the performance of the advanced timer-based assembly algorithm, we set M = 50. Figure 4.8 shows the impact of parameter α on the burst loss ratios for different traffic loads. It shows that the burst loss ratio decreases as α decreases. On the other hand, the average edge buffering delay increases as α decreases, as shown in Figure 4.9.

How to choose α is a tradeoff between the burst loss ratio and the average edge buffering delay. A suitable α should be able to achieve a low burst loss ratio while not increasing the edge buffering delay too much. From Figures 4.8 and 4.9, we can see that when α is smaller than 0.1, the burst loss ratio decreases slowly and is almost the same as the one for α = 0.1 while the average edge buffering delay obviously increases.

Regarding the performance of the DBA scheme, Figures 4.10 and 4.11 show the impact of N_r and T_wait on the average burst loss ratios for a low traffic load (0.3) and for a high traffic load (0.89), respectively. In these figures, the curve “aL” denotes the burst loss ratio when T_wait is set to a times the average burst length (L). The initial offset time is set to 30 ms. The results indicate that as N_r and T_wait increase, the burst loss ratio decreases. However, when T_wait exceeds the average burst length duration and N_r exceeds 4, the burst loss ratios decrease slowly and eventually become almost the same. Thus, in the simulations we set 0.4 ms (average burst length duration = average burst length (50 Kbytes)/bandwidth (1 Gbps)) and 4 as the default values of T_wait and N_r.

Figure 4.8 Impact of α on burst loss ratio.

Figure 4.9 Impact of α on edge buffering delay.

Figure 4.10 Average burst loss ratios versus N_r with traffic load 0.3.

Figure 4.11 Average burst loss ratios versus N_r with traffic load 0.89.

Regarding the performance of the integrated scheme presented in this section, the results obtained by simulation show that the proportions of different classes are close to the ratios of predefined parameters and are independent of the traffic load for the integrated scheme. Therefore, the integrated scheme achieves proportional differentiated services for multiclass traffic. Figure 4.12 shows the end-to-end BHP queueing delay normalized to the average burst length duration for each class during transmission.

We can see that the lower priority bursts have larger queueing delay than do the higher priority bursts. For example, the queueing delay is several microseconds for class 2, tens of microseconds for class 3, and hundreds of microseconds for class 4. The simulation results show that although the integrated scheme improves the burst loss performance at the expense of increasing extra offset time, the increase of end-to-end delay is very small (at most hundreds of microseconds) and would be negligible for real applications. As an advantage over the existing priority schemes, our integrated scheme does not need any complex burst segmentation or wavelength preemption support, so it has a simple implementation. Moreover, it provides controllable and predictable proportional differentiated services for each class.

Figure 4.12 End-to-end BHP queueing delay.

4.5  Fractal approaches in Internet traffic simulation

4.5.1  Using parallel discrete-event simulations (PDES) for scalability evidence in large-scale networks modeling

Large-scale networks are a class of complex systems made of a large number of interacting individual elements with a finite number of local state variables each assuming a finite number of values. The dynamics of the local state variables are discrete events occurring in continuous time. We assume that between two consecutive updates, the local variables stay unchanged. Another important assumption is that the interactions in the underlying system to be simulated have finite range. Often the dynamics of such systems is inherently stochastic and asynchronous. The simulation of such systems is rather nontrivial and in most cases the complexity of the problem requires simulations on distributed architectures, defining the field of parallel discrete-event simulations (PDES) (Toroczkai et al. 2006). Conceptually, the computational task is divided among N processing elements (PE-s), where each processor evolves the dynamics of the allocated piece. Due to the interactions among the individual elements of the simulated system, the PEs must coordinate with a subset of other PEs during the simulation. In the PDES schemes, update attempts are self-initiated and are independent of the configuration of the underlying system, thus their performance also becomes independent. The update dynamics, together with the information sharing among PEs, make the parallel discrete-event simulation process a complex dynamical system itself. In fact, it perfectly fits the type of complex systems we are considering here: the individual elements are the PEs, and their states (local simulated time) evolve according to update events, which are dependent on the states of the neighboring PEs.

The design of efficient parallel update schemes is a challenging problem, due to the fact that the dynamics of the simulation scheme itself is a complex system, whose properties (efficiency and scalability) are hard to deduce using classical methods of algorithm analysis. Since one is interested in the dynamics of the underlying complex system, the PDES scheme must simulate the physical time variable of the complex system. When the simulations are done on a single-processor machine, a single time stream is sufficient to time-stamp the updates of the local configurations, regardless whether the dynamics of the underlying system is synchronous or asynchronous. When simulating asynchronous dynamics on distributed architectures, however, each PE generates its own virtual time, which is the physical time variable of the particular computational domain handled by that PE. In conservative PDESs schemes, a PE will only perform its next update if it can obtain the correct information to evolve the local configuration (local state) of the underlying physical system it simulates. Specifically, when the underlying system has nearest-neighbor interactions, each PE must check the interaction topology of the underlying system to see if those are progressed at least up to the point in virtual time where the PE itself did. Based on the fundamental notion of discrete-event systems that the state of a local state variable remains unchanged between two successive update attempts, we have developed a framework for simulation of jobs scheduling on a parallel processing platform.

4.5.1.1  Parallel platform model

The proposed model for the platform consists of P processor units. Each processor p_i has capacity c_i > 0, i = 1,2,…, P. The capacity of a processor is defined as its speed relative to a reference processor with unit-capacity. We assume for the general case that c₁ ≤ c₂ ≤ … ≤c_P. The total capacity C of the system is defined as $C={\displaystyle {\sum }_{i=1}^P{c}_i}$. A system is called homogeneous when c₁ = c₂ … = c_p. The platform is conceived as a distributed system. The distributed-system, as shown in Figure 4.13, consists of P machines connected by a network.

Figure 4.13 The model of the distributed platform.

Each machine is equipped with a single processor. In other words, we do not consider interconnections of multiprocessors. The main difference with multiprocessor systems is that in a distributed system, information about the system state is spread across the different processors. In many cases, migrating a job from one processor to another is very costly in terms of network bandwidth and service delay, and that the reason that we have considered for the beginning only the case of data parallelism for a homogenous system. The intention was to develop a scheduling policy with two components. The global scheduling policy decides to which processor an arriving job must be sent, and when to migrate some jobs. At each processor, the local scheduling policy decides when the processor serves which of the jobs present in its queue.

Jobs arrive at the system according to one or more interarrival time processes. These processes determine the time between the arrivals of two consecutive jobs. The arrival time of a job j is denoted by A_j. Once a job j is completed, it leaves the system at its departure time D_j. The response time R_j of job j is defined as R_j = D_j − A_j. The service time S_j of job j is its response time on a unit-capacity processor serving no other jobs; by definition, the response time of a job with service time s on a processor with capacity c′ is s/c′. We define the job set J(t) at time t as the set of jobs present in the system at time t:

$J\left(t\right)=\left\{j\right|A_j\le t<D_j\}$

For each job j ∈ J(t), we define the remaining work $W_j^r\left(t\right)$ at time t as the time it would take to serve the job to completion on a unit-capacity processor. The service rate ${\text{σ}}_j^r\left(t\right)$ of job j at time t (A_j ≤ t < D_j) is defined as ${\text{σ}}_j^r\left(t\right)=\underset{\text{τ}\to t}{\lim }\text{d}{W}_j^r\left(\text{τ}\right)/\text{d}\text{τ}$. The obtained share ${\text{ω}}_j^s\left(t\right)$ of job j at time t (A_j ≤ t < D_j) is defined as ${\text{ω}}_j^s\left(t\right)={\text{σ}}_j^r\left(t\right)/C$. So, ${\text{ω}}_j^s\left(t\right)$ is the fraction of the total system capacity C used to serve job j, but only if we assume that $W_j^r\left(t\right)$ is always a piecewise-linear, continuous function of t. Considering $W_j^r\left(A_j\right)=S_j\text{\hspace{0.17em}and\hspace{0.17em}}{W}_j^r\left(D_j\right)=0$ we have ${\displaystyle {\int }_{A_j}^{D_j}{\text{ω}}_j^s\left(t\right)\text{d}t}={\displaystyle {\int }_{A_j}^{D_j}{\text{σ}}_j^r\left(t\right)\text{d}t}=S_j/C$.

One can define an upper bound on the sum of the obtained job shares of any set of jobs {1,…,J} as

${\text{ω}}_{\max }\left(t\right)=C^{-1}{\displaystyle \sum _{i=1}^{\min \left(J,P\right)}{c}_i}$

(4.16)

Since Equation 4.1 imposes upper bonds on the total share, the maximum obtainable total share at time t is defined as

$m^T\left(t\right)=C^{-1}{\displaystyle \sum _{p=1}^{\min (\left|J\left(t\right),P)\right|}{c}_p}$

(4.17)

In a similar manner, for a group g of processors (g = 1, 2, …, G), the maximum obtainable group share at time t is defined as

$m^G\left(t\right)=c^{-1}{\displaystyle \sum _{p=1}^{\min (\left|J_g\left(t\right),P)\right|}{c}_p}$

(4.18)

Let consider as an example a system with P = 3, c₁ = 2 şi c₂ = c₃ = 1. For simplicity, we assume that there is no job migration and that jobs are only served by processor 1, or wait in its queue. At time t = 0, job 1 with service time S₁ = 4 enters the system, job 0 is already present, $W_0^J(0)=2$. There are no other jobs present in the system, nor do any other jobs arrive. We consider the first-come first-served (FCFS) policy. Figure 4.14 shows the Gantt chart for the execution of the two jobs (0 and 1) and Figure 4.15 shows the remaining work $W_1^J(0)=2$, the service rate ${\text{σ}}_1^J(t)$, and the obtained share of job $o_1^J(t)$.

4.5.1.2  Share-scheduling policy for parallel processing

Let consider the above mentioned model of a parallel processing platform with P processors, and assume that each job j has a weight w_jp on processor p, representing the fraction of time job j spends on processor p. We consider also that job j can switch between processors such that it appears to be served by more than one processor at the same time, at total service rate of ${\displaystyle {\sum }_{p=1}^P{w}_{jp}{c}_p}$ and the following conditions are respected:

$\begin{array}{ccc}0\le w_{jp}\le 1,\text{\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}j, p;}& {\displaystyle \sum _j{w}_{jp}\le 1\text{\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}p;}}& {\displaystyle \sum _p{w}_{jp}\le 1\text{\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}j}}\end{array}$

Figure 4.14 The Gantt chart for the FCFS policy.

Figure 4.15 Job’s scheduling parameters for the FCFS policy.

Under these assumptions, the proposed policy defined as job-priority multiprocessor sharing (JPMPS) can be applied without difference for both multiprocessors and distributed systems with free job migration. Under JPMPS, jobs 1, …, J (J ≥ 1) can be given service rates ${\text{σ}}_1^J\ge {\text{σ}}_2^J\ge \dots \ge {\text{σ}}_J^J,J>0$, if and only if, for j = 1, …, J,

${\displaystyle \sum _{k=1}^j{\text{σ}}_k^J}={\displaystyle \sum _{p=1}^{\min \left(k,p\right)}{c}_p}$

(4.19)

When we compare this result to the definition of m^T(t) in Equation 4.2 and m^G(t) in Equation 4.3 it is obvious that, under JPMPS, the set of jobs present in the system can always be provided with a share of m^T(t) and also all jobs of group g can be provided with m^G(t).

The objective of share scheduling is to provide groups with their feasible group shares. For each group one can define a constant share, the required group share $r_g^G$, as the fraction of the total system capacity c that group g is entitled to, with $\text{Σ}{r}_g^G=1$. The required group shares are assumed to be constant over time and to be known in advance to the system. When the required group shares of two groups are the same, the system should treat them equally, and when one exceeds the other, the system should give preferential treatment to the group with the $r_g^G$. The required group share plays an important role in the definition of the feasible group share, because the feasible group share depends only on the required group share, the number of jobs present of the group and the average processor capacity.

We state the following three requirements for the definition of the feasible group share $f_g^G\left(t\right),g=1,\dots ,G$:

1.  $0\le f_g^G\left(t\right)\le m_g^G\left(t\right)$

2.  $f_g^G\left(t\right)\text{\hspace{0.17em}depends only on\hspace{0.17em}}\left|J_g\left(t\right)\right|,r_g^G,P,c_i\left(i=1,\dots ,P\right)$

3.  $\text{if\hspace{0.17em}}\left|J_g\left(t\right)\right|\ge P\text{\hspace{0.17em}then\hspace{0.17em}}{f}_g^G\left(t\right)=r_g^G$

The first requirement means that we should not promise to a group more than the maximum we can provide. The second requirement means that the feasible group share only depends on the number of jobs of the group and not on the coincidental presence of jobs of other groups (i.e., groups are promised a share of the system that does not depend on the activity of other groups). The third requirement states that when the number of jobs in a group exceeds a threshold, the feasible group share equals the required group share. This threshold may be different for different groups, provided they have different required group shares.

From requirements 2 and 3, it follows that:

$\begin{array}{ccc}{f}_g^G\left(t\right)\le r_g^G& \text{and}& {\displaystyle \sum _{\text{g}}{f}_g^G\left(t\right)\le 1}\end{array}$

(4.20)

This means one can never promise more than the total system capacity to all groups together.

Because Internet is a spontaneously grown collection of connected computers, we have utilized our PDES model for solving current problems due to the distributed computation on the Internet, when often the computed tasks have little or no connection to each other. Therefore, complex problems can be solved in real time on the Internet if the task allocation problem, which is rather complex by itself, is solved. However, if we assume that task allocation is resolved and the PE communication topology on the Internet is a scale-free network, the scalability properties of a PDESs scheme on such networks still remain to be emphasized.

With this aim, we have studied the fundamental scalability problem of conservative PDES schemes where events are self-initiated and have identical distribution on each PE using as model of scale-free networks the Barabási–Albert model. The scalability properties have been studied for a causally constrained PDES scheme hosted by a network of computers where the network is scale-free following a “preferential attachment” construction. The simulation exhibited slow logarithmic decay as a function of the number of PEs. The numerical results confirm the validity of any scalable parallel simulation for systems with asynchronous dynamics and short-range interactions.

4.5.2  Evidence of attractors in large-scale networks models

One of the most interesting theoretic and applied scientific result the quantification of how can be evidenced the attractors in dynamic systems which can be modeled by complex networks. In this aim, for the main three models (EA, Erdös–Rényi; BA, Barabási–Albert; and WA, Watts–Strogatz) analyzed in this chapter, we tried to observe specific events, where each state variable (associated to each node) is used to represent a specific prototype pattern (attractor). By assuming that the attractors spread their influence among its neighboring nodes through a diffusive process, it is possible to overlook the specific details of specific dynamics and focus attention on the separability among such attractors. Costa developed a study where this property is defined in terms of two separation indices (one individual to each prototype and the other considering also the immediate neighborhood) reflecting the balance and proximity to attractors revealed by the activation of the network after a diffusive process (Costa 2007). The separation index also considering the neighborhood was found to be much more informative, while the best separability was observed for the Watts–Strogatz model. The effects of the involved parameters on the separability were investigated by correlation and path analyses. The obtained results suggest the special importance of some measurements in underlying the relationship between topology and dynamics.

In order to infer the influence of the topologic features on the dynamics properties (i.e., attractor separation) correlation analysis and path analysis were applied. A series of interesting results were obtained regarding not only the separation indices, but also the importance of several local and global topologic features on the overall attractor separation. The simulation results confirm the correlation and path analyses of the effects of the topologic features of the network on the respective attractor separability.

In the same direction is oriented the study of the influence of the geometrical properties of the complex networks on the dynamics of the processes supported by the network infrastructure (for example, routing problems, inference, and data mining). In real growing networks, topological, structural, and geometrical properties emerge spontaneously from their dynamical rules. Nevertheless we still miss a model in which networks develop an emergent complex geometry, but a fractal analysis can confirm that a single two parameter of a network model, the growing geometrical network, can generate complex network geometries, combining exponential growth and small-world properties with finite spectral dimensionality. In one limit, the nonequilibrium dynamic rules of these networks can generate scale-free networks with clustering and communities.

In particular, growing complex networks evolving by the preferential attachment mechanism have been widely used to explain the emergence of the scale-free degree distributions which are ubiquitous in complex networks. In the next chapter, the interdependence between the fractal properties of the network topology and the self-similar aspect of the information flow will be highlighted and explained.