How interesting would it be to be able to read the thoughts of others? There they are, walking down the street or sitting idly in a train or bus, and their eyes tell little or nothing of what is going on inside their heads. What do they think about? What schemes, what puzzles, what dreams, what mysteries, are they turning over in their minds? It might not be interesting at all, for it is possible that, whether working or idling, so many of these people are not interested, and who is not interested is not interesting. Their minds may just be turning over the most humdrum little worries, or odds and ends of gossip, or merely futile fantasies. In this case, the power to read thoughts would be a dubious gift—the mastery of a language with an exceedingly dreary literature.
But surely there must be times when the thoughts of the dullest person are wonderful. Of course, we use the word “wonderful” in two senses: “I have just had a wonderful time,” or “This is a most wonderful universe.” In the first sense, “wonderful” is just an exaggeration for pleasant or amusing. In the second, it means what it says—full of wonder, of fascination, mystery, and interest. Yet the two senses are not always separate, because a life that has been spent in wondering will almost certainly have been a wonderful life. Most children seem to be having an interesting time, for the world is a new thing in their eyes, and they are always asking questions. The more one asks, and gets answers to, questions, the more are the questions to be asked, for the more we know, the more we know we don’t know. The size of the mystery always grows in proportion to the increase of knowledge. Discovery is always, to some extent, the finding of new things about which you are ignorant.
A person who has given up asking questions, who has ceased to wonder, has stopped living because he has stopped growing. For life is like a stream in the sense that it must flow on or cease to be a stream. And where the mind of man ceases to flow out in wonder and interest towards the ocean of reality that surrounds him, it turns back upon itself and becomes a stagnant pool. A person who is miserable or bored is one whose mind has turned back upon itself, a person who gets in the way of his own experience, who frets over how he feels and how he would like to feel, and yet always seems to feel the same—frustrated. Yet all this turning back, this self-concern, is like a snake trying to make a good meal off his own tail—a futile procedure that makes him gag, and that boils down to the ultimate absurdity of trying to feed on one’s own hunger.
Obviously, then, life is interesting and wonderful to the extent that one has interest in it and wonder for it. It is superficially wonderful if you wonder only at superficial things, and deeply wonderful if you wonder at deep things. To wonder what Mrs. Smith will wear for the party, what would have happened if you had been the son of a millionaire, what the dentist will have to say about your teeth, or whether it will be a fine weekend, is to wonder only at surfaces. It seems astonishing that there can be minds that never go deeper, that never want to know who or what is the mysterious power of consciousness that looks out through Mrs. Smith’s eyes, how it is that I am myself and not someone else, why it is that I love pleasure and hate pain, or how there comes to be a sun that can shine.
It is difficult to imagine many questions more interesting than these. Yet the asking and answering of them is a process called philosophy, which is popularly thought to be one of the drier subjects in a college curriculum as well as one of the most unprofitable professions. If such things are dry and dull, life is then dry and dull at its very core, and one must just as well commit suicide without further ado. This is, perhaps, what our world is doing. Its daily life must be such a round of inane tedium that it can think of nothing better to do with the marvels of atomic fission than make a sensational bang, and blow itself up.
Needless to say, philosophy is not just another course in college, or the wearing out of one’s mind with volumes of incomprehensible verbiage. Philosophy, as Aristotle said, begins and ends in wonder—wonder at what lies beneath the surface, not only of the sun, moon, and stars, but also of the most trivial and commonplace events. Every child is born a philosopher. Not only does he take things apart to find out how they work, but also he asks the most profound questions as to who made God, whether space goes on forever, what happened before anything happened, whether he would have been born if Mother had married someone else, why this, why that, why anything and everything. It is tragic that this spontaneous venture of wonder and interest in the roots of life bogs down either in parental annoyance, or in university courses where gentlemen expert in chopping logic dismiss all such questions as meaningless.
In a very strict sense it may be meaningless to ask why there is a universe, or whether I might have been someone else than me. But if the human mind had never wondered at these things, there would have been no physics, no chemistry, no biology or astronomy. Perhaps a question that has no answer is a meaningless question, but we can never find this out until we are sure it has no answer. And the good scientist is never quite sure, being the least dogmatic of people.
For many hundreds of years the scientific mind has been trying to find out what things are—what stones and stars and men are made of. Reducing them to simpler elements, it wants to know, in turn, what these are made of. Finding that men and mountains and air are arrangements of such simpler things as carbon, oxygen, sulfur, and hydrogen, and that these are composed of molecules, and these of atoms, and these of electrons, protons, and neutrons, we begin to wonder how much further we can go, how much longer we can ask, “What is it made of?” For we have brought everything down to such a fine point, that the investigation is now rather like trying to stick the point of a needle into the point of a needle. If the mind of man is of the same substance as the universe that it investigates, must there not come a time when the whole inquiry is just a single substance trying to define itself—like a mouth trying to kiss itself or a flame to burn itself?
At present there does seem to be a tendency among scientists to feel that this “main line” of inquiry has reached its limits, as if the mind had reached an impenetrable wall, and must henceforth be content to explore its surface. In a remarkable passage in The Evolution of Physics Einstein and Infeld (1938) say:
In our endeavor to understand reality we are somewhat like a man trying to understand the mechanism of a closed watch. He sees the face and the moving hands, even hears its ticking, but he has no way of opening the case. If he is ingenious he may form some picture of a mechanism which could be responsible for all the things he observes, but he may never be quite sure his picture is the only one which could explain his observations. He will never be able to compare his picture with the real mechanism and he cannot even imagine the possibility or the meaning of such a comparison. (p. 38)
Back at the end of the nineteenth century, Maxwell foresaw the same problem, and explained it with an illustration employing a cabinet instead of a watch. Imagine a cabinet whose doors are forever sealed, but in each door there is a minute hole from which there extends a string. When we pull string A, string B goes up, and conversely. The scientist can but note the regularity of this event. As to what goes on inside the cabinet—whether A and B are two ends of one string, or whether there is some more complex mechanism—he can only speculate; he can never know for certain.
If physics cannot penetrate the watch or the cabinet, or if its method of inquiry has reduced itself to a needle trying to prick the point of a needle, must the whole problem be brought to a close? Must it be said that any further questioning as to what reality is, is meaningless? One may say so, and yet the human mind will go on wondering, because unsatisfied with the answer. The problem is simply whether it is entirely useless and absurd to do so.
The very analogy employed by Einstein and Infeld (1938) suggests an answer. Strictly speaking, the function of science may be simply to observe, measure, and predict the movements of the watch’s hands and the rhythm of its ticking. Beyond this point, no observation is possible, and no measurement. But in fact, the scientist does form theories of what lies inside the watch, and tests them by the degree to which they enable him to predict what the watch will do. In this respect science enters the realm of philosophy and metaphysics, which is the act of wondering about the inside of the watch or the cabinet, about the depths of reality that are beyond the experience of the senses.
The philosopher forms and tests his theories in somewhat the same way as the scientist. He develops an idea of what may be inside the watch and responsible for its external movements from things that he has seen outside the watch. Outside, he has observed the things that make movements and noises similar to those of the watch, as well as the processes that cause them. He then reasons that the movements and noises of the watch must have similar causes, assuming that the relation of cause and effect that exists outside must also exist inside.
To these theories he applies a test not unlike the scientist’s test of prediction. He asks whether his theories enable man to make a better adaptation to the world. If they do so, he assumes that his theory is in harmony with, or corresponds to, the unknown reality that causes this world. But this is not all. The problem of adaptation to the future course of events is not the philosopher’s only or even chief concern. For he realizes that it is of no use to be able to predict and adjust oneself to the future unless you are also capable of having harmony with life in the present. Lacking this, you are always preparing for a tomorrow that never comes. You predict, but do not fully enjoy the fruits of prediction and planning when they become present.
Therefore the philosopher also loves philosophy for itself. He finds that wondering is perhaps the highest form of enjoyment, because in this act he loses himself in the contemplation of the most fascinating of all things—the reality that lies beyond the senses. All enjoyment, all real happiness involves this loss of self-consciousness through absorption in something wonderful. Can there, then, be any other higher happiness than absorption in the “highest” mystery—the unseen reality that underlies this whole universe? In the words of Goethe, “The highest to which man can attain is wonder; and if the prime phenomenon makes him wonder, let him be content; nothing higher can it give him, and nothing further should he seek for behind it; here is the limit.”
We come, then, to the barrier that the scientists say they cannot pass unless they join hands with the philosophers and begin to speculate and wonder. This wondering is no useless reaching into the void, and no mere attempt to satisfy curiosity. The correct solution to many of the problems of living in this everyday world depend upon accurate reasoning about the world beyond the senses. For this other world is in no way remote from the world of practical life; it is really the same world, understood more deeply. It is as if we were traveling across a sheet of ice. The senses can see, as it were, only the surface, and other means must be used to discover where the ice is thick enough to carry our weight, and so to decide what course the journey must take.
We must be prepared, however, for reasoning about the unseen to lead us to some strange conclusions. Already the scientists have found that their own theories of “the world below the surface” are very hard to describe in concrete images. They speak of space being curved, and how can we imagine space with a curve in it, as if it were the film of a soap-bubble without, however, either an inside or an outside? While we shall always use concrete images for purposes of illustration, it must nevertheless be remembered that these are only images, and that what we are talking about is not exactly like them. A familiar example of this difficulty may be seen in trying to draw a cube on a flat surface.
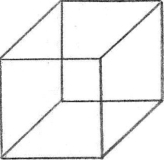
To represent a cube on this flat sheet of paper, we draw two squares, and then join their corners with straight lines (see figure 1.1). But this figure is not a cube. For all the angles of a cube are right angles, but in this drawing many of them are not. Yet because we know what a real cube is, we can imagine one from this drawing by using the convention of perspective. Because we are familiar with a world of three dimensions, we can easily understand representations of this solid world upon a flat surface where there are only two dimensions.

Figure 1.1. A Necker Cube representing a three-dimensional perspective.
Supposing, however, there were people living in a world of two dimensions, people who had never seen, and had no idea of a third. They would find it most difficult to understand this drawing. A line perpendicular to their world would seem to them like a point, a surface like a line, and a solid like a surface. They would see the drawing here only as two squares with triangles adjoining them. Thus we are somewhat like these inhabitants of “Flatland” in our attempts to understand the world beyond our senses. Indeed, it took many centuries for our own ancestors to understand how this earth could be spherical, because to their limited point of view it seemed so flat. How could anyone walk on the underside of such a globe without falling off?
It is easy enough to see how the inhabitants of “Flatland” could not understand our drawing of a cube. It is fairly easy to put ourselves in their position by doing something else to our drawing. Here is the square. Think of it as made by moving the upright line at the left (one dimension) over to the right (two dimensions) (see figure 1.2). Here we have the two dimensions of length and breadth. Now by moving the whole square through the third dimension of depth, we have once more the cube (see figure 1.3). So far the figure is quite understandable. But now let us suppose that there is still another dimension, at right angles to each one of the three. We move the whole cube through this dimension, and get what is called a tesseract (see figure 1.4).

Figure 1.2. A square representing a two-dimensional perspective.
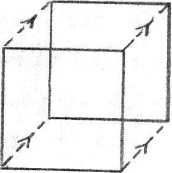
Figure 1.3. A Necker Cube representing acquisition of a three-dimensional perspective.
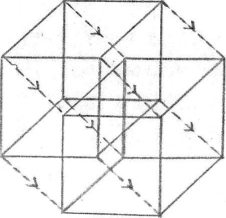
Figure 1.4. A tesseract representing a four-dimensional perspective.
Now you can feel like the people in “Flatland,” for you are looking at a drawing of a four-dimensional cube, which is something you cannot possibly imagine. Thus thinking about a four-dimensional world in terms of three is not unlike thinking about the unseen world in terms of the seen. We can represent it, but not exactly.
We know, then, that one of the chief characteristics of our ordinary, everyday world is that it has three dimensions. What are some of its other important characteristics? Perhaps the most obvious is that everything is, without exception, in a state of movement and change. Every planet moves around its sun. Every sun and star moves around other suns and stars. Every solid object is in fact a cluster of pulsating electrons. Not only is every form in motion, but at the same time every form is inconstant, changing in shape and substance rapidly (as the smoke) or extremely slowly (as the rocks). In the words of the Greek philosopher Heraclitus, “Everything flows,” and even
The hills are shadows,
And they flow from form to form,
And nothing stands.
Hardly less obvious is the fact that all known things exist only in relation to each other. In the first place, they depend on each other. Every thing is an effect, and thus depends upon some cause. There can be no life apart from water, air, and sunlight; no air and water without an earth; no earth without a sun; no sun without a galaxy of stars; no stars without space, time, and energy—and so on to we know not what extent. In the second place, our knowledge of this world depends entirely upon the relation of contrasts or opposites. Light is unimaginable without darkness. Long is meaningless save by contrast with short. Substance is unthinkable without space, motion without relative stillness, heat without cold, fast without slow, hard without soft, sound without silence, pleasure without pain, and life without death. Indeed, it is absolutely impossible to express a meaning without making a contrast, or to think of a thing that is in no way distinguished from something else.
The known world is then a world of change and relativity. Everything changes, and everything is relative to some other thing. We have never come across anything entirely permanent and absolute. Must we therefore conclude that there is nothing unchanging, eternal, and absolute?
This is, indeed, the picture of the universe that is presented by many of the most influential thinkers of our time—a world of pure relativity in which there is no single stable element. It is something like an infinitely tall skyscraper where floor stands upon floor, but no floor stands on solid ground. From the height at which we now stand, we can look down (into the past), and see the building disappearing to a “vanishing point” in an immense well of space. But if there is no solid ground on which the whole structure can stand, the floors must descend for ever beyond this vanishing point, standing on each other and on nothing else. Or, to change the illustration, such a universe is not unlike a nation where each individual makes his living, not out of the soil, but by taking in his neighbor’s washing. Such a nation would be as economically unstable as the skyscraper would be architecturally unstable. The entire structure would be a process of collapse.
But we need never entertain such fantastic pictures if we look carefully at the idea on which they are based—the notion that “Everything is relative; everything is in a state of change.” For in fact these statements do not mean anything at all. They are pure nonsense.
We saw that such ideas as change, motion, and energy had meaning only because of their opposites. “Change” is a meaningful word, an understandable process, only in relation to stillness or permanence. We recognize change by comparing it with something unchanging. If, then, everything changes, how do we know that it changes, since there is nothing permanent in relation to which it changes? We might just as well say, “Everything is half,” or “Everything is up,” or, for that matter, “Everything is blah.”
But if such things as change and permanence exist only in relation to each other, can we not say that “Everything is relative”? Certainly the same rule must apply. The word “relative” is meaningless when applied to everything. Indeed, there is something fundamentally peculiar about these “Everything is” statements. None of them make sense. And the peculiar thing is this: to say something about everything is to say nothing about everything! It is like painting a picture that is all one color: you have no picture.
We can go further. If it makes no sense to say “Everything is relative,” it does not even make sense to say “Everything is.” To say that everything has existence adds absolutely nothing to one’s knowledge of the universe, for one is not actually saying anything about everything. It is merely to say, “Every thing which exists, exists.” In other words, “A rose is a rose.” So what?
We can begin to see, now, what is the real difficulty with these statements. In making them we have used many words that actually mean something—“thing,” “relative,” “is,” “change,” “exists.” I can say, “Some things (such as planets and men) exist,” and make sense because I am implying that “Some things (such as gryphons and goblins) do not exist.” Obviously, then, the difficulty is simply in the word “everything.” It cannot mean anything unless it has an opposite. But if it does not have an opposite, it will be impossible for us to form any ideas at all about the world, the universe that we experience as a whole.
So we must ask the question, “Is there anything else besides everything?” It may sound like a silly question, but if the answer is “No,” we shall have to take the word “everything” out of the dictionary as a mere meaningless noise. Who, then, are the candidates for the position of the opposite of everything?
The first to be examined is obviously “Nothing.” This is a strange candidate who has to be disqualified at once, having the odd defect of not even appearing for the examination. He is not. Furthermore the word “nothing” cannot be used in any sensible statement as the opposite of everything. I can say, “There is nothing in this box,” and make sense. But if nothing is the opposite of everything, I should also be able to say, “There is everything in this box,” and still make sense. But I can’t.
In other words, to oppose everything to nothing is simply not to oppose it to anything. If no other opposite can be found, the idea of everything, of the universe itself, is in a most precarious position. And if the idea is precarious, what about the reality? For surely the two are inseparable. Surely the word “everything” has meaning in that it denotes a reality—the reality of all stars, all galaxies, all bodies in space and time, all processes, all relations, all electrons. Yet apparently these things, all things, are like some princess in a story-book who must find a husband or be beheaded. Nothing, in other words, no husband, simply won’t do.
What, then, could be the opposite that will make the idea and the reality of everything both meaningful and possible? For if this opposite is to be some thing, as distinct from nothing, will not this something already be included in “everything” and so still be unable to be its opposite?
Indeed, it seems as if the strangeness of reality will have to surpass every flight of fancy that myth, legend, or fairy-tale has ever conceived. For the prince who can save the princess from having her head chopped off must be neither a nothing nor a something, for a nothing is no husband, and a something is the princess herself.
It depends, of course, on what we mean by a thing. For to talk about all things is actually to talk about all stars, electrons, etc., that is, about all relative things. If the Flatlanders were to talk about all things, they would be meaning all things in their world of two dimensions. But we know of other things, such as cubes, which would be outside their definition of all things.
Let us suppose that the relative world that we know is like a map, but an incomplete map in the sense that it has edges or margins at which roads, rivers, and oceans simply come to an abrupt end. These edges are the limits of our sense-knowledge. Now science gives us theories of what lies beyond these edges, but these theories have a particular limitation. The scientist looks at the map, and sees that on the map itself every road leads to a town and every river to an ocean—except those that run off the edge. He cannot see how these end. But he reasons that roads and rivers running off the map will do the same things as those on the map: they will lead to other towns and other oceans. His theories as to the positions of these other towns and oceans may be most ingenious. He may deduce that two roads that, at the point of leaving the map, have been approaching each other will probably lead to the same town. But this particular kind of reasoning leads only to the idea of more towns, more roads, more rivers, and more oceans.
Yet the philosopher wants to know whether this map is simply one section of a surface that goes on for ever and ever. Is there anything else, he asks, besides indefinite map, indefinite towns, roads, and rivers? Is there anything else besides everything?—“everything” being defined as a surface bearing towns, roads, and rivers.
Now the philosopher knows, from evidence within his experience, that you cannot have unsupported surfaces. He has never seen any object that was simply a surface, much less a surface indefinitely extended. He knows that every surface is finite, and is the outside of a solid. If you travel across a surface, you will go round the solid and return to the same place. He reasons that the same will be true of the map. Follow any road far enough off the map, and you will return to the same place on the map—sometime—whether the shape of the underlying solid be spherical, cubic, ovoid, or pyramidal.
The same process of reasoning suggests, therefore, that the known universe is part of a finite system. It is not galaxies of stars and areas of space extending for ever and ever, still less a series of effects and causes going backwards for ever and ever in a straight line of time—a skyscraper standing on nothing. Underlying the finite surface is a solid; underlying two dimensions is a third; underlying the map is the terrestrial globe. But just as the Flatlanders cannot conceive a third dimension, a cube or sphere, so we have difficulty in conceiving the kind of “Something” that would underlie the “everything” that we know with our finite senses.
Nevertheless, it is reasonable and necessary to suppose that this “Something” exists as the solid, the opposite, supporting and giving meaning to all that we know. It is not in the class of relative things, just as the sphere is not in the class of surfaces, and the earth not in the class of towns, roads, rivers, and oceans.
It is furthermore reasonable to conclude that if all known things are relative and changing, spatial and temporal, the “Something” that supports them and gives them both meaning and existence by contrast, will be absolute and permanent, spaceless and timeless. For want of a better name, we shall call it the Absolute.
When you take a voyage into unknown latitudes, you must remember that you cannot remain on course without making corrections for wind and currents. Similar “corrections” must be made, and held constantly in mind, in trying to go beyond time and space into the realm of the Absolute. Remember that you cannot represent a cube on a flat surface without using the convention, the trick, of perspective. You represent the third dimension with lines that are still in two dimensions. Similarly, when you want to show, on a flat map, that the earth is spherical you draw curved lines of longitude, or draw each “side” of the globe within a circular border. This results in distortions and inaccuracies, which will be confusing if it is forgotten that “tricks” have been used.
Representing the globe on a flat map is like trying to talk and think about the Absolute. The two dimensions of the map correspond respectively to time and space, and the human mind cannot think except in terms of time and space. Alternatively, we can think of the two dimensions of the map as corresponding to the fact that we have to think in terms of opposites. Because the mind is part of the relative world, it cannot possibly escape this limitation.
Therefore we can only talk about the Absolute by using a convention. To avoid confusion, we must be clear from the start as to what this convention is, and constantly make “corrections” for it. In brief, the convention is that we must talk about the Absolute as if it were another relative thing. Otherwise we should not be able to talk it at all, for we have no language, no ideas, at our disposal other than the relative.
This will be clarified if we rehearse, in another way, the argument that compels us to admit that there is an Absolute. Experience shows us nothing whatsoever that is not dependent on something else. No part of this universe can exist without dependence on, and relation to, other parts. This is relativity. But it is simple to understand that if everything is dependent, the universe cannot exist. For if absolutely everything is dependent, there is nothing on which it depends.
It does not help in the least to try to get out of this dilemma by making the dependent universe infinite, for you do not get an independent thing by adding many dependent things together. A hat hangs on a peg attached to a hat that hangs on a peg attached to a hat. … However large this hat-chain may be, it collapses unless it finally arrives at some fixed and independent peg. Hanging all by itself, it is absurd, like the grin of the Cheshire Cat in Alice in Wonderland, which hung in the air when the cat had vanished. To make the chain infinite is only to make it infinitely absurd. This is not a solution of the problem. It is merely the indefinite postponement of a solution. Nor does it help to hang the last hat on a peg attached to the first, making the process of dependence circular. It still collapses.
But we know that there are things, and that all known things are dependent. We are thus forced to the conclusion that there must be some unknown thing that is independent—that does not hang on anything because it does not need to. If there is not, then there cannot be any dependent things. But there are!
In our known world there are only relatively independent things. That is to say, there are only things that are independent of some things. For instance, hat No. 4 on the chain will be independent of 3, 2, and 1, but dependent on 5 and all those above. For us, then, the terms dependent and independent are relative. They have meaning only by contrast with each other. We cannot really think or conceive a thing independent of all other things, because every known thing is dependent.
To put it in another way: we describe and know things by their relations with each other. We know light by contrast with darkness. Light without darkness, or darkness without light, are alike inconceivable. Similarly, a relative, or dependent, world is meaningless save by contrast with an absolute or independent. But it should follow, logically, that an absolute is inconceivable without the relative. If so, we shall only be saying that the independent must depend on the dependent, or that the absolute can exist only in relation to the relative. But this will amount to saying that it is neither absolute nor independent!
This is the inescapable limitation of our two-dimensional way of thinking. We are compelled to think of the Absolute as the opposite of the relative, because we can only think in opposites—in relativities. This is the convention that we must use if we are to think of the Absolute at all; we have to represent it as something relative, as, on the surface, the solid must be represented by something flat. Therefore we have to remember this correction: the Absolute is the opposite of the relative, without which the relative could have neither meaning nor existence. But it is not opposed to the relative in the same way that relative things, such as light and darkness, are opposed to each other. The difference is this: whereas the relative cannot exist without the Absolute, the Absolute can exist without the relative. If it could not, it would not be the Absolute because it would depend on the relative.
This proposition is only illogical in the same sense that the angles of a cube drawn on a flat surface are not all right angles. Logic is simply the law of relativity. It corresponds to the fact that on a flat surface—in the world of relativity—you can only have length and breadth. You may draw a third line to represent depth, but in fact it will still lie in the dimensions of length and breadth, and your statement that it forms right angles with the other two lines will seem absurd—i.e., illogical. But it is only illogical if there are no other dimensions than length and breadth.
Similarly, it is only illogical to speak of the Absolute if “everything is relative.” But logic itself is enough to show that the statement, “Everything is relative,” is meaningless. Thought, in other words, requires something beyond itself that it cannot define, just as the existence of a surface requires an underlying solid that cannot, however, be actually represented in terms of surface.
Now we can never arrive at the Absolute by indefinite extension of the relative, just as we shall never get the idea of the solid from the indefinite increase of the surface—unless, perhaps, the surface bends back on itself and we return to our starting-point. This was the weakness of the old arguments for the Absolute that tried to prove that events must run back to a First Cause in time. Beyond every time you can always imagine an earlier time, beyond every hat you can always conceive another hat. Logically, you need never arrive at the first time, or the fixed hat-peg. But because you need never do so, logic itself is indicating that the direction of your search is futile.
We ask, “On what does this dependent universe depend?” We look back and back into time, or out and out into space, to find only more and more dependent things. In this direction we never arrive at anything final. The only gain from this quest is an increasing sense of the absurdity of a purely relative cosmos.
Our thinking must, therefore, take a new departure—a jump into a new dimension, not following time and space for ever, but, as it were, turning off at right angles to them. This will give us a very different picture of the First Cause than the old picture of the Original Push that, aeons ago, started the universe off. The universal process is not, so to speak, a row of bricks falling down because God pushed the first brick (see figure 1.5). We shall find the First Cause not so much at the temporal beginning of everything as at the present root of everything. Picture time as a sphere, like the astronomers’ curved space. The Origin of this sphere, the First Cause, the Absolute, will not be anywhere on the sphere, but “inside” it (see figure 1.6). This shows us all the events in time, and for that matter in space too, radiating from the First Cause. Only we must be careful to remember that this is a “conventional” picture, and that there is not actually any space or time between the center and any point on the outside.

Figure 1.5. “The First Cause.”
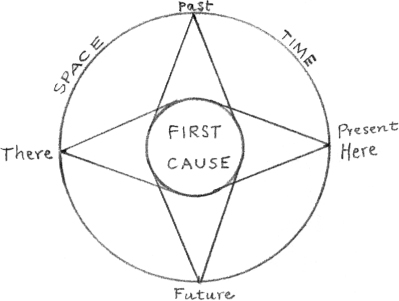
Figure 1.6. Events in time radiating from the First Cause.
Around the outside of this sphere all events depend on one another in a complex network that has no observable beginning or end. But while each depends on the others, all depend on the center—that does not depend on anything at all.
Something analogous to this idea of the Absolute as the “center” of all things is found in modern physics. For in asking, “What makes the universe tick?” physics has found that the most profitable line of inquiry has not been the investigation of an unobservable past, nor even the plumbing of fathomless space. The most fruitful results have come from looking into the heart of things, asking not “What made them as they are?” but “What makes them as they are?” In such a way we seek the First Cause neither in an immeasurably distant past, nor in a heaven beyond the uttermost nebulae. We seek it within the electrons that constitute our being at this moment.
The clue, then, to an understanding of the Absolute is that the relative world requires an opposite in order to exist, since by itself relativity is meaningless. But this opposite is not within the scheme of relativity, for which reason, it does not require the relative. Between relative things, opposition is mutual and reciprocal. But in the Major Dyad of Absolute and Relative, the opposition is “one way only.”
Keeping this peculiar relationship in mind, we can understand certain properties of the Absolute simply by contrasting it with properties of the relative. Other properties of the Absolute can be suggested by asking what kind of reality would be sufficient to cause all various qualities and relations of the known universe.
We saw that among the chief characteristics of the relative world were time, space, and change. By contrast, these imply that the Absolute is eternal, infinite, and immutable. But in using these words, we must be careful not to confuse them with certain popular and incorrect senses that custom has attached to them.
To the average man eternal means everlasting, eternal life being a life that goes on through endless time without ceasing. But this somewhat nightmarish idea has nothing to do with eternity in its true sense. For eternity is not time—much less unending time. Time is perhaps not easy to define. When asked what time was, St. Augustine replied, “I know, but when you ask me I don’t!” Yet if we consider what we mean by time, it is easy to see that it means at least this—the experience, or occurrence, of events in a one-way stream of succession. Time is really change—a process in which events come one after another in an irreversible order. In our basic diagram of the Absolute and the Relative, time is motion round the outer circle, so that B is after A and before C. A, B, and C stand in successive order (see figure 1.7).
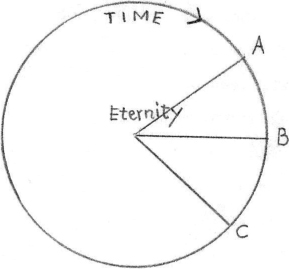
Figure 1.7. Relations of time and eternity.
But from the standpoint of the center, from which the whole surface “radiates,” A, B, and C are all equally present, for we saw that there is neither time nor space between the center and any point on the circumference. Eternity is, then, a standpoint from which all events are not successive but simultaneous. When you look at your hand, you can see all five fingers at once, even though they are distant from each other in space. Supposing, however, that the five fingers are five distant points of time—the years 1900, 1905, 1910, 1915, and 1920. Eternity is a point of reference to which these five points of time are as present as your fingers are present to you.
Or again: if you walk into a dark room with a flashlight that casts a thin beam, you will only be able to know what is in the room by shining the bean upon one small section after another, successively. This is like the viewpoint of time. But if you turn on the main light in the ceiling, you will see the whole room at once, having a view somewhat like that of eternity. Eternity is therefore a sort of permanent moment, in which all times are now.
Somewhat the same principles underlie the true meaning of infinity. To say that the Absolute is infinite is not to say that it is indefinitely immense, like a space going outward for ever and ever. As eternity is a point of reference to which all times are now, infinity is a point of reference to which all places are here. This is why it is possible to say that the Absolute is everywhere, or omnipresent, not like a gas that is diffused, but as something that is present at every point of space in its entirety. Infinity in the “immense” meaning, would not be true infinity at all: it would be ordinary, relative space.
Likewise, to say that the Absolute is immutable is not to say that it is static—i.e., that it remains without change or movement for an interminable period of time. This is merely relative stillness—the stillness of a rock as compared with the stillness of a river. A static stillness of this kind could hardly be responsible for all the motions of this universe. The Absolute is immutable because it does not change, and it does not change because its whole action and existence is simultaneous—not successive. The “action” by which it causes the relative world requires no effort, that is, no crossing of space or perpetuation through time. The action by which it caused the lighting of the first suns is the same identical action by which it now causes the vibration of a mosquito’s wing. There has been no change, for it does all things at once.
Although, to this point, we have said several things about the Absolute, we have not actually said what it is. We have said that it is, because a purely relative world requires it as its necessary opposite. We have said what it is not, because, by opposition to the relative world, we find it to be nontemporal, nonspatial, and nonchangeable. But we are never going to be able to say what it is, because human thought and language can only answer the question “What?’ by standing outside the object to be described, and comparing it with other things. But we cannot stand outside the Absolute without immediately ceasing to exist. Every point from which one might look at it is a point “inside” it, and the very ability to look is a power that the Absolute supplies. Now if our eyes cannot look at themselves, if the knower cannot know himself, how much less can we see and know the Origin of sight and knowledge.
In the act of knowing, the knower knows that he is. He also knows that he is not the things that he knows, as the eyes are not the things that they see. Our knowledge of the Absolute is, then, similar to this obscure knowledge of ourselves, since we know that we are and what we are not, rather than what we are. We cannot stand outside ourselves to see what we are. This kind of knowledge of the Absolute may make it seem something peculiarly vague and negative.
But still another kind of knowledge is possible, knowledge based on the fact that, because everything in the relative world depends on the Absolute and is caused by it, the nature of the Absolute must be adequate to produce this world. Let us suppose for a moment that the Absolute is some kind of blind force, like electricity—a force essentially blind and unconscious and mechanical. Would a force of this kind be able to produce the everyday world that we know? To many people, this seems possible enough, for if a blind force were to go on shaping and re-shaping itself long enough, the chances are that it would eventually shape itself into this form—this form that we call life, knowledge, beauty, order, and so forth.
The idea may seem plausible, but it has a fatal flaw. If I assert that the Absolute, the basic force of the universe, is unconscious and unintelligent, I must also assert that I myself, and my conscious mind, are parts and products of this force. The idea that this is so will also have to be part of it, because it is part of my mind. But if myself, my mind, and my idea, are nothing but special forms of unintelligent force, how can I assert that this idea is intelligent? For I am really saying this: “My idea that the basic force of the universe is unintelligent is itself a form of this unintelligence!” If so, it is not an intelligent idea.
If I am to claim that my own mind is in any sense conscious or intelligent, I am bound to admit that the force that shapes it is at least conscious and intelligent. To say that consciousness is a special form of unconsciousness, and intelligence a special form of unintelligence, is to say that the presence of a certain power is a special form of its absence. This comes perilously close to saying that something is a special form of nothing.
Nonsense of this kind is the inevitable result of denying to the First Cause at least the properties and faculties that we ourselves enjoy. This is not to say, however, that the Absolute is conscious and intelligent in the same way that we are. It is saying that if it can cause intelligence, it must not only be at least intelligent, but, indeed, something more than intelligent.
The reason for this “more” is that the less is always the result of the greater, never the greater of the less. Take, for example, the power of heat. Something that is merely warm does not, all by itself, become hot. More heat is not simply the result of less heat. The increase of heat must be derived from something most hot—such as fire. Similarly, more life (or more intelligence) does not just “evolve” all by itself from less life, or no life—for this would imply again the nonsense that the presence of a power is the result of its absence. What we call evolution is the progressive derivation of life from something that is most alive—as water gets hotter and hotter, and finally turns into steam, by deriving heat progressively from the fire beneath it.
We can see, then, that the evolution of consciousness and mind from the relatively blind world of vegetable and mineral nature is progressive sharing in the life and power of the Absolute. This implies that the more we are able to share in the life of the Absolute, the more conscious, the more intelligent, we can become. For this reason, knowledge of the Absolute is no mere philosophical pastime, but a matter of the highest possible importance. It can carry us yet further in the course of evolution, and lead to possibilities of life and knowledge beyond our dreams.
This, indeed, is what is implied in the truth that the Absolute is not only our “origin,” but also our “goal.” In the traditional language of philosophy, the Absolute is known both as the First Cause and as the Final Cause—that is, the end toward which the universal process moves, as well as the point from which it begins.
To understand this point, we must remember again that as the world-process does not start from the Absolute in time, neither does it disappear into it in time. Our diagram of the Absolute-Relative relationship is seen in figure 1.8:
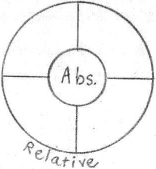
Figure 1.8. The absolute-relative relationship.
Not this (figure 1.9):
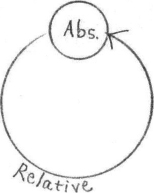
Figure 1.9. An incorrect view of the absolute-relative relationship.
This is only to say that the relative world never was, and never will become, the same thing as the Absolute. By its nature, the Absolute is not relative, and could not become relative without ceasing to be Absolute. The same is true in reverse. The relative is not the Absolute, and could not become the Absolute without ceasing to exist.
The process of becoming lies only around the circle. There is no becoming as between the circle and its center, for becoming requires time, and between circle and center there is no time. When water boils over the fire, it does not become fire, even though fire is the cause of its boiling. It becomes hot water, and eventually steam. In other words, it becomes as like fire as water can become. In the same way, the relative world “surrounding” the unchanging fire of the Absolute will, in time, become as like the Absolute as relative things can become.
To know, then, what the Absolute is like in terms of relative things and relative knowledge, to represent the Absolute in the form of the relative, is to move toward the goal and perfection of relative existence. Thus the task of philosophy is to show man where he is going—the end toward which all his activities must be directed if they are not to be in vain.
Einstein, A., & Infeld, L. (1938). The evolution of physics. The growth of ideas from early concepts to relativity and quanta. Cambridge, UK: Cambridge University Press.
Reprinted from an unpublished work-for-hire (1950, Franklin J. Matchette Foundation) with permission of Nell S. Ernst, President of the the Franklin J. Matchette Foundation.