
Predicting Individual Behavior
Suppose that a person must choose among three alternatives (A, B, C) and is observed to choose A. Now let this person be faced with a new decision problem, in which he or she must choose between A and B, alternative C not being available. Can the decision be predicted?
This is an extrapolation problem, so the answer must depend on what one is willing to assume. A mainstream economist would predict that the chosen alternative remains A. The reasoning is that the observed selection of A over B and C reveals this person to prefer A to B. Removing alternative C from the choice set does not disturb this fact.
This is perhaps the simplest application of revealed preference analysis, the approach economists routinely use to predict individual behavior. To make predictions, economists combine empirical evidence with behavioral assumptions. The data are observations of actual choices made by members of the population of interest. The basic behavioral assumption is rational choice: each member of the population orders alternatives in terms of preference and chooses the most preferred alternative among those available.
The assumption of rational choice suffices to make some extrapolations from observed choices. One has already been given. Another concerns a person whose behavior is observed in two decision settings. In the first setting, the person must choose between A and B, and is observed to choose A. In the second setting, the same person must choose between B and C, and is observed to choose B. Transitivity of preferences implies that if this person were required to choose between A and C, he or she would choose A.
More ambitious extrapolations require stronger assumptions than rational choice alone. Economists often observe the choices made by a sample of persons in certain decision settings, and wish to predict the choices that would be made by other members of the population in other decision settings. Extrapolations of this kind become possible when rational choice is accompanied by assumptions restricting the form of preferences.
This chapter begins by describing the practice of revealed preference analysis. Revealed preference analysis needs to be well understood even by those who do not accept its premises. Other social scientists often criticize as implausible the behavioral assumptions underlying econometric predictions. But criticism in the absence of a constructive alternative has only limited effectiveness. The other social sciences have not developed any coherent and widely applicable competitor to revealed preference analysis, and thus this approach continues to dominate efforts to extrapolate individual behavior.
I shall use my own revealed preference analysis of college-going behavior, performed with David Wise, to describe the main features of present-day econometric practice. Manski and Wise (1983, chaps. 6 and 7) used observations from the National Longitudinal Study of the High School Class of 1972 (NLS72) to estimate a rational-choice model of college enrollment. We then used the estimated model to predict the impact of the Pell Grant program, the major federal college scholarship program, on enrollment.
The NLS72 survey, commissioned by the National Center for Education Statistics, provides schooling, work, and background data on almost 23,000 high school seniors drawn from over 1,300 high schools in the United States in spring 1972. Data were obtained through a series of questionnaires distributed to the respondents and their high schools and through periodic follow-up surveys.
The starting point for our analysis was to assume that the patterns of college enrollment and labor force participation observed among the NLS72 respondents are the consequence of decisions made by these students, by colleges, and by employers. Colleges and employers make admissions decisions and job offers that determine the options available to each high school senior upon graduation. Each senior selects among the available options.
What do the NLS72 data reveal about the decision processes generating post-secondary activities? If we assume that a student chooses the most preferred alternative from the available options, then observations of chosen activities partially reveal student preferences. In particular, if we imagine a student as implicitly assigning a numerical utility value to each potential activity, then the fact that the student has chosen a particular activity implies that its utility exceeds that of all others that the student could have chosen.
For simplicity, assume that after high school graduation a student has two alternatives: γ = 1 is college enrollment and γ = 0 is work. (The model actually estimated assumed multiple alternatives.) If we observe that NLS72 respondent n chose to go to college, then we may infer that Un1 ≥ Un0, where Un1 and Un0 are the utilities that this respondent associated with college and work. If respondent n chose to work, then Un0 ≥ Un1. The NLS72 data provide a large set of these inequalities, one for each respondent.
The preference inequalities implied by observations of these activity choices do not provide sufficient information to allow us to predict how a student not in the sample would select between college and work, or how a student in the sample would have behaved if conditions had differed. To extrapolate behavior, we must combine the NLS72 sample information with assumptions restricting the form of preferences.
For example, we might assume that the utility of college enrollment to student n depends on his ability An and his parents’ income In, and also on the quality Qn and cost Cn of his best college opportunity. Similarly, the utility of working might depend on his best potential wage Wn. In particular, suppose that the utilities are known to have the linear form
(5.1a) Un1 = β1An + β2In + β3Qn + β4Cn
and
(5.1b) Un0 = β5Wn,
where β ≡ β1, . . . , β5 is a parameter vector that is unknown but assumed not to equal zero.1 Observe that γ is assumed not to vary across students. For now, all students with the same value of (A, I, Q, C, W) are assumed to have the same preferences.
Given data on the actual activity γn chosen by student n and data measuring the utility determinants (An, In, Qn, Cn, Wn), the revealed preference inequality

implies restrictions on the possible values of the parameters β. The NLS72 data yield an inequality of the form (5.2) for each respondent, and β must satisfy all of these inequalities.
Suppose that only one nonzero value of β satisfies all of the revealed preference inequalities implied by the NLS72 choice data. Then this must be the actual value of β. We can now predict the schooling/work decisions of students whose values of (A, I, Q, C, W) differ from those actually observed among the NLS72 respondents. For example, if i designates a student whose best college has attributes (Ai, Ii, Qi, Ci) and whose best job opportunity has wage Wi, this student i may choose to work if
(5.3a) β5Wi = β1Ai + β2Ii + β3Qi + β4Ci
and definitely chooses to work if
(5.3b) β5Wi > β1Ai + β2Ii + β3Qi + β4Ci.
The utility function of our example has a fairly simple form. An actual empirical study might pose determinants of utility beyond (A, I, Q, C, W) and loosen the assumption that these determinants act on utility in linear fashion; see, for example, the specification of Manski and Wise (1983). It is not reasonable to expect, however, that any empirical study will have access to data that express all the determinants of student decision making. Therefore economists assume that utilities vary as a function of variables that are known to decision makers but unobserved by the researcher.
In our example, these unobserved variables may be represented through real numbers un1 and un0 added to the utilities specified in (5.1). Thus we now generalize (5.1) to
(5.4a) Un1 = β1An + β2In + β3Qn + β4Cn + un1
and
(5.4b) Un0 = β5Wn + un0.
With this change, the preference inequalities revealed by the NLS72 data become
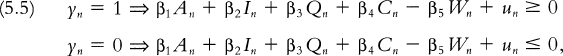
where un ≡ un1 – un0.
From the perspective of the researcher, the unobserved u is a random variable with some distribution across the population of students. So the utilities Un1 and Un0 are themselves random variables, and we have a random utility model of behavior. Assuming that the distribution of u is continuous, the probability that a student with observed characteristics (A, I, Q, C, W) chooses to enroll in college is2
(5.6) P(γ = 1 | x) = P(xβ + u ≥ 0 | x),
where x ≡ (A, I, Q, C, W). Equation (5.6) does not assert that a student with characteristics x actually behaves probabilistically. The equation asserts that a researcher is only able to make probabilistic predictions of student behavior.3
Given a random sample of realizations of (γ, x), the choice probability P(γ = 1 | x) can be estimated nonparametrically on the support of P(x). Our objective in deriving the random utility model representation of P(γ = 1 | x) on the right side of (5.6) is to enable prediction of γ off the support.
A random utility model has no identifying power in the absence of information restricting the distribution of the unobserved variable u. Perhaps the easiest way to see this is through inspection of the revealed preference inequalities (5.5). Given any hypothesized value for the parameters β and any NLS72 respondent n, one can always find a value of un that satisfies (5.5). So the NLS72 choice data imply no restrictions on β.
The model becomes informative when sufficiently strong assumptions are imposed on the distribution of u across the population of students. The prevailing practice in empirical studies has been to assume that u is statistically independent of x, with a distribution known up to normalizations of location and scale.4 In particular, suppose it is known that u has the standard logistic distribution. Then the choice probabilities have the form of the familiar logit model

With the distribution of u specified in this way, the NLS72 data can be used to estimate the parameters β. This done, the right side of (5.7) can be used to predict the schooling behavior that would occur under conditions different from those faced by the NLS72 respondents.5
Manski and Wise (1983) estimated a random utility model that is more complex than the one just described, but not qualitatively different. The estimated model was used to study the impact on freshman college enrollments of the Basic Educational Opportunity Grant (BEOG) program, later renamed the Pell Grant program. This federal scholarship program was initiated in 1973, so the NLS72 respondents were not eligible at the time of their initial post-secondary schooling decisions. Thus our prediction problem was clearly one of extrapolation rather than prediction on the support.
In the context of our random utility model, the BEOG program influences behavior by changing the college costs, C, that students face. Given knowledge of the program eligibility criteria and award formula, we estimated the cost of college to any given student in the presence of the program. This done, we predicted how the NLS72 respondents would have behaved had the program been in operation. We then aggregated these predictions across the sample to generate predictions of aggregate freshman college enrollments in the United States.
Table 5.1 presents some of our findings concerning the version of the program that was in effect in 1979. The predictions indicate that the BEOG program was responsible for a truly substantial increase (59 percent) in the college enrollment rate of low-income students, a moderate increase (12 percent) in middle-income enrollments, and a minor increase (3 percent) in the rate for upper-income students.
Overall, we predicted that 1,603,000 of the 3,300,000 persons who were high school seniors in 1979 would enroll in full-time post-secondary education in 1979—80. In contrast, only 1,324,000 would have enrolled had the BEOG program not been in operation. The findings indicate that the enrollment increases induced by the existence of the program were totally concentrated at two-year and vocational schools. Enrollments at four-year schools were essentially unaffected.
Table 5.1 Predicted enrollments in 1979 with and without the BEOG program (in thousands)

Source: Manski and Wise (1983), table 7.4. Reprinted by permission of Harvard University Press, copyright 1983 by the President and Fellows of Harvard College.
Federal scholarship programs with varying eligibility criteria and award formulae have been proposed, but only a few programs have actually been implemented. Our revealed preference analysis of college enrollments makes it possible to predict the impacts of a wide variety of proposed and actual programs. This ability to extrapolate is very powerful.
The price of extrapolation is the set of assumptions imposed. The assumption of rational choice alone yields only limited ability to extrapolate. The real power of revealed preference analysis emerges when the rational-choice assumption is combined with restrictions on the form of preferences. Our analysis of college choice indicates the kinds of preference assumptions commonly imposed in empirical studies.
I would like to call particular attention to one of the assumptions routinely imposed in applications of revealed preference analysis. Rational choice is a subjective concept. Individuals are assumed to choose the most preferred alternative, given their perceptions of the options available. There is no requirement that these perceptions be “correct” or “objective” in any sense.
Our discussion of revealed preference analysis has thus far avoided this critical matter by implicitly assuming that researchers know how decision makers perceive their alternatives. We assumed that high school graduates perceive their options to be college enrollment and labor force participation. We supposed that our measurements of student ability A, family income I, college quality Q and cost C, and potential wage W correspond to the way students perceive these factors.
There is often reason to question whether researchers really know how decision makers perceive their alternatives. I continue to focus on the case of schooling choice, which provides a good illustration.6
Economists analyzing schooling decisions assume that youth compare the expected outcomes from schooling and other activities and then choose the best available option. Viewing education as an investment in human capital, we use the term returns to schooling to refer to the outcomes from schooling relative to nonschooling.
Given the centrality of the expected returns to schooling in economic thinking on schooling behavior, it might be anticipated that economists would make substantial efforts to learn how youth perceive the returns to schooling. But the profession has traditionally been skeptical of subjective data, so much so that we have generally been unwilling to collect data on expectations. Instead the norm has been to assume that expectations are formed in specific ways.
Economic studies of schooling behavior have routinely assumed that all youth possess the same information and process this information in the same manner. But researchers have differed substantially in their assumptions about the information that youth possess and the way they process it. I give three examples.
Freeman (1971) analyzed the major field decisions of male college students. He assumed that each person chooses the field offering the highest expected lifetime income. Moreover, he assumed that expectations formation is myopic. Each person believes that, should he select a given college major, he would obtain the mean income realized by the members of a specified earlier cohort who did make that choice.7
Willis and Rosen (1979) analyzed the college enrollment decision of male veterans of World War II. They assumed that a person chooses to enroll if the expected lifetime income associated with enrollment exceeds that of not enrolling. They assumed that youth condition their income expectations on their ability. They also assumed that youth have rational expectations, that is, that youth know the actual process generating lifetime incomes conditional on their ability and schooling. Willis and Rosen hypothesized that each youth applies his knowledge of the process generating lifetime incomes to predict his own future income should he enroll or not enroll in college.
In the Manski and Wise (1983, chap. 6) analysis of college choice, the utility of enrolling in a given college was assumed to depend on a student’s own Scholastic Aptitude Test (SAT) score and on the average score of students enrolled in that college. Youth were not assumed to know the lifetime incomes realized by earlier cohorts or the actual process generating incomes. Instead they were assumed to believe that the returns to enrolling depend on their own SAT score and the average at the college.
Unfortunately, there is no evidence supporting any of the assumptions economists have made about expectations of the returns to schooling. If anything, there are logical and empirical reasons to think otherwise.
The logical point is that youth seeking to infer their own returns to schooling face the same selection problem as do social scientists seeking to infer treatment effects. Youth and social scientists may possess different data on realized incomes, may have different knowledge of the economy, and may process their information in different ways. But both want to use their data and knowledge to learn the returns to schooling conditional on the available information. Youth, like social scientists, must confront the selection problem.
There is no empirical evidence that youth cope with the selection problem in any of the ways assumed in the studies cited. In fact, there is indirect evidence suggesting that youth form expectations in heterogeneous ways. Although we lack data on youths’ expectations, we have extensive data on the practices of labor economists studying the returns to schooling. During the past thirty years, labor economists have executed hundreds of empirical studies of the returns to schooling. Reading this vast literature reveals that researchers vary greatly in the conditioning variables used, in the outcome data analyzed, and in the handling of the selection problem.
Compare, for example, Willis and Rosen (1979) with Murphy and Welch (1989). The former study analyzes data from the NBER-Thorndike Survey, estimates returns to schooling conditional on measured ability, and is explicitly concerned with the effect of unmeasured ability on the selection of students into schooling. The latter piece analyzes data from the Current Population Surveys, which contain no ability measures, and implicitly assumes that the selection of students into schooling is unrelated to ability. If experts can vary so widely in the way they infer the returns to schooling, it is reasonable to suspect that youth do as well.
Our lack of understanding of the way youth perceive the returns to schooling figures prominently in the ongoing policy debate about the best way to influence the behavior of those youth considered at risk of dropping out of high school.
One line of thinking begins from the premise that remaining in school is generally in students’ self-interest. If so, youth who drop out of school must misperceive the returns to schooling. Hence we should provide these youth with information that convinces them of the value of schooling. We should correct the misperceptions that presently lead youth to make poor schooling decisions.8
A second line of thinking begins from the premise that students perceive the returns to schooling correctly. If students choose to drop out, it is because they know that the returns to schooling are low.9 This perspective implies that the key to improving school performance is better incentives. We should make sure that students who stay in school are rewarded and that those who do not are sanctioned.10
In the absence of evidence on how youth actually perceive the returns to schooling, policymaking goes on in the dark. Programs embodying many combinations of information and incentives are continually proposed and implemented across the country, with no basis for judging their effectiveness.11
Suppose that one wants to extrapolate individual behavior but finds the assumptions of revealed preference analysis to be unpalatable. If the only data available are observed choices, then the only option is to invoke other assumptions that one finds more palatable. But new data collection may open up new inferential possibilities.
It is often possible to elicit from people statements describing how they would behave when facing various decision problems. For example, female respondents in the June 1987 Supplement to the Current Population Survey (CPS) were asked this question:
Looking ahead, do you expect to have any (more) children?
YesNoUncertain
(U.S. Bureau of the Census, 1988a)
Respondents in the National Longitudinal Study of the High School Class of 1972 (NLS72) were asked these questions in fall 1973:
What do you expect to be doing in October 1974?
(Circle one number on each line)
| Expect to be doing | Do not expect to be doing | |
| Working for pay at a full-time or part-time job | 1 | 2 |
| Taking vocational or technical courses at any kind of school or college | 1 | 2 |
| Taking academic courses at a two-year or four-year college | 1 | 2 |
| On active duty in the Armed Forces (or service academy) | 1 | 2 |
| Homemaker | 1 | 2 |
(Riccobono et al., 1981)
Social scientists have long asked survey respondents to answer such unconditional intentions questions, and have used the responses to predict actual behavior. Responses to fertility questions like that in the CPS have been used for over fifty years to predict fertility (see Hendershot and Placek, 1981). Data on voting intentions have been used to predict American election outcomes since the early 1900s (see Turner and Martin, 1984). Surveys of buying intentions have been used to predict consumer purchase behavior since at least the mid-1940s (see Juster, 1964).
Social scientists also sometimes ask survey respondents to answer conditional intentions questions posing hypothetical scenarios. For example, a conditional-intentions version of the CPS fertility question might be
Imagine that the government were to enact a child-allowance program providing families with fifty dollars per month for each dependent child. Assuming that this program were in operation, would you expect to have any (more) children?
YesNoUncertain
The long history of intentions surveys notwithstanding, social scientists continue to differ in their interpretation of stated intentions and in the use they make of these data. Just as revealed preference analysis requires assumptions about the structure of preferences, interpretation of stated intentions requires assumptions about how people respond to the questions posed and how they actually behave. Social scientists disagree on these matters and so disagree on the interpretation of intentions data. It is particularly intriguing to contrast the perspectives of social psychologists and economists.
Social psychologists take intentions very seriously. They suppose that intention is a mental state that causally precedes behavior and that can be elicited through questionnaires or interviews. The influential work of Fishbein and Ajzen (1975) makes intention the intermediate variable in a behavioral model wherein (1) intentions are determined by attitudes and social norms and (2) behavior is determined by intentions alone.
According to Ajzen and Fishbein (1980), a person’s behavioral intention is his subjective probability that the behavior of interest will occur. (They refer to the response to a yes/no intentions question as choice intention.) It seems, however, that social psychologists do not use the term “subjective probability” as a statistician would. Ajzen and Fishbein (1980, p. 50) state “we are claiming that intentions should always predict behavior, provided that the measure of intention corresponds to the behavioral criterion and that the intention has not changed prior to performance of the behavior.” In a review of attitudinal research, Schuman and Johnson (1976, p. 172) write that the Fishbein-Ajzen model implies that “the correlation between behavioral intention and behavior should approach 1.0, provided that the focal behavior is the same in both cases and that nothing intervenes to alter the intention.” It is difficult to reconcile these statements with the idea that behavioral intention is a subjective probability, unless that probability is always zero or one.
In practice, social psychologists typically measure intention on some nominal scale (Ajzen and Fishbein, 1980, for example, recommend a seven-point scale for which the verbally described responses range from “likely” to “unlikely”) and report the arithmetic correlation between this measure and the behavioral outcome. See, for example, Schuman and Johnson (1976) and Davidson and Jaccard (1979).
In recent times, economists have mostly ignored intentions data. The dominant view is deep skepticism about the credibility of subjective statements of any kind. Early in their careers, economists are taught to believe only what people do, not what they say. Economists often assert that respondents to surveys have no incentive to answer questions carefully or honestly; hence, there is no reason to believe that subjective responses reliably reflect respondents’ thinking.12
The economics discipline has not always been so hostile to the use of intentions data to predict behavior. From the mid-1950s through the mid-1960s, analysis of consumer buying intentions was close to a mainstream activity. Juster (1964, 1966) reviewed this literature and made original contributions of interest.
Considering the problem in which the behavior of interest is a binary purchase decision (buy or not buy) and the intentions question is also binary (intend to buy or do not intend to buy), Juster (1966, p. 664) wrote “Consumers reporting that they ‘intend to buy A within X months’ can be thought of as saying that the probability of their purchasing A within X months is high enough so that some form of ‘yes’ answer is more accurate than a ‘no’ answer.” Thus he hypothesized that a consumer facing an intentions question responds as would a statistician asked to make a point prediction of a future event.
Perhaps intentions data reveal a mental state that causally precedes behavior. Perhaps they provide statistical predictions of behavior. Or perhaps Webster’s Eighth New Collegiate Dictionary (1985, p. 629) is accurate when it states: “Intention implies little more than what one has in mind to do or bring about.”
In the absence of consensus about the interpretation of stated intentions, it is of some use to place bounds on the predictive power of these data. The lower bound is necessarily zero. We cannot exclude the possibility that stated intentions reveal nothing about future behavior. To determine an upper bound, we might consider this thought experiment:
Imagine ideal survey respondents who are fully aware of the process determining their behavior. What are the most informative responses that such ideal respondents can provide to intentions questions?
We shall study this thought experiment in the particularly simple context of intentions questions calling for yes/no predictions of binary outcomes (see also Manski, 1990b).
Let i and γ be binary variables denoting the survey response and subsequent behavior respectively. Thus i = 1 if a person responds “yes” to the intentions question, and γ = 1 if behavior turns out to satisfy the property of interest.
Suppose that a researcher observes a random sample of intentions responses i and respondent attributes x and is thus able to infer the distribution P(i, x). The researcher, who does not observe respondents’ subsequent behavior γ, wishes to learn the choice probabilities P(γ | x, i) and P(γ | x); the former choice probability conditions on stated intentions and the latter does not. The inferential question is: What does knowledge of P(i, x) reveal about P(γ | x, i) and P(γ | x)?
I address this question under the assumption that (1) survey respondents are aware of the actual process determining their future behavior; and (2) given the information they possess at the time of the survey, respondents offer their best predictions of their behavior, in the sense of minimizing expected loss (see Section 1.2). When these conditions hold, intentions data are said to provide rational-expectations predictions of future behavior. The term rational expectations is routinely used by economists but should not be confused with the unrelated concept of rational choice.
A person giving a rational-expectations response to an intentions question would begin by recognizing that future behavior will depend in part on conditions known at the time of the survey and in part on events that have not yet occurred. A woman responding to the CPS fertility question, for example, should recognize that her future childbearing will depend not only on her current family and work conditions, which are known to her at the time of the survey, but also on the future evolution of these conditions, which she cannot predict with certainty.
Let s denote the information possessed by a respondent at the time that an intentions question is posed. (In the case of a conditional intentions question, s includes the information provided in the statement of the hypothetical scenario.) Let u represent uncertainty that will be resolved between the time of the survey and the time at which the behavior γ is determined. Then γ is necessarily a function of (s, u), and so may be written γ(s, u). I shall not impose any restrictions on the form of the function γ(s, u). In particular, behavior need not be determined by a rational-choice process.
Let Pu | s denote the actual probability distribution of u conditional on s. Let P(γ | s) denote the actual distribution of γ conditional on s. The event γ = 1 occurs if and only if the realization of u is such that γ(s, u) = 1. Hence, conditioning on s, the probability that γ = 1 is
(5.8) P(γ = 1 | s) = Pu[γ(s, u) = 1 | s].
A respondent with rational expectations is assumed to know γ(s, ·) and Pu | s at the time of the survey; hence she knows P(γ = 1 | s).
The respondent is assumed to give her best point prediction of her future behavior, in the sense of minimizing expected loss. The best prediction necessarily depends on the losses the respondent associates with the two possible prediction errors, namely, (i = 0, γ = 1) and (i = 1, γ = 0). Whatever the loss function, however, the best prediction must satisfy the condition
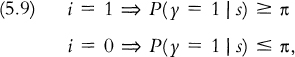
for some threshold value π ∊ (0, 1) that depends on the loss function. This formalizes the idea stated by Juster (1966). An alternative statement of (5.9) that will be used below is13
(5.9′) P(γ = 1 | s, i = 0) ≤ π ≤ P(γ = 1 | s, i = 1).
Prediction of Behavior Conditional on Intentions
Consider a researcher who wishes to predict a survey respondent’s future behavior γ, conditional on her stated intention i and some attributes x observed by the researcher. That is, the researcher wishes to determine P(γ | x, i). The researcher does not know the stochastic process Pu | s generating future events or the function γ(s, u) determining behavior.
A researcher who only knows that intentions are rational-expectations predictions can draw no conclusions about P(γ | x, i). There are two reasons. First, if the respondent’s threshold value π is unknown, equation (5.9′) imposes no restrictions on P(γ = 1 | s, i). Second, if the information s possessed by the respondent is unknown, knowledge of P(γ = 1 | s, i) implies no restrictions on P(γ = 1 | x, i).
Conclusions can be drawn if
(a) the researcher knows π and includes π among the variables x, and
(b) respondents know the attributes x, so s subsumes x.
Then stated intentions reveal whether P(γ = 1 | x, i) is below or above π. To see this, observe that if condition (b) holds, the law of iterated expectations implies that
(5.10) P(γ = 1 | x, i) = E[P(γ = 1 | s, i) | x, i].
If condition (a) holds, all persons with the same value of x share the same threshold value π. So (5.9′) and (5.10) together imply that
(5.11) P(γ = 1 | x, i = 0) ≤ π ≤ P(γ = 1 | x, i = 1).
Prediction Not Conditioning on Intentions
Researchers often want to predict the behavior of nonsampled members of the population from which the survey respondents were drawn. Intentions data are available only for the sampled persons, so the predictions cannot now condition on i. Instead, the quantity of interest is P(γ = 1 | x).
Given conditions (a) and (b), the bound (5.11) obtained on P(γ = 1 | x, i) implies a bound on P(γ = 1 | x). Observe that
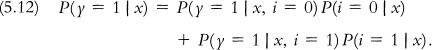
Random sampling identifies the intentions probabilities P(i = 0 | x) and P(i = 1 | x), but we only know that the choice probabilities P(γ = 1 | x, i = 0) and P(γ = 1 | x, i = 1) lie in the intervals [0, π] and [π, 1], respectively. Hence (5.12) implies this sharp bound on P(γ = 1 | x):
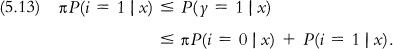
Observe that the bound width is πP(i = 0 | x) + (1 − π) P(i = 1 | x). If π = 1/2, the bound width is 1/2 for all values of P(i | x).
It has been known for more than twenty-five years that intentions probabilities need not equal choice probabilities. That is, the relationship
(5.14) P(i = 1 | x) = P(γ = 1 | x)
need not hold (see Juster, 1966, p. 665). Never-theless, some of the literature has considered deviations from this equality as “inconsistencies” in need of explanation. For example, Westoff and Ryder (1977, p. 449) state: “The question with which we began this work was whether reproductive intentions are useful for prediction. The basic finding was that 40.5 percent intended more, as of the end of 1970, and 34.0 percent had more in the subsequent five years. ... In other words, acceptance of 1970 intentions at face value would have led to a substantial overshooting of the ultimate outcome.” That is, the authors found that P(i = 1 | x) = .405, and subsequent data collection showed that P(γ = 1 | x) = .340. Seeking to explain the observed “overshooting,” the authors state: “One interpretation of our finding would be that the respondents failed to anticipate the extent to which the times would be unpropitious for childbearing, that they made the understandable but frequently invalid assumption that the future would resemble the presentߜthe same kind of forecasting error that demographers have often made.” More recent demographic studies continue to presume that deviations from (5.14) require explanation. See, for example, Davidson and Beach (1981) and O’Connell and Rogers (1983).
Rational-expectations prediction does imply (5.14) in the special case where future behavior depends only on the information s available at the time of the survey. Then a survey respondent can predict her future behavior with certainty. So i must equal γ. But (5.14) need not hold if events u not known at the time of the survey partially determine future behavior. A simple example makes the point forcefully.
Suppose that respondents to the CPS fertility question report that they expect to have more children when childbirth is more likely than not; that is, π = 1/2. Suppose that the actual probability of having more children is always .51; that is, P(γ = 1 | s) = .51 for all s. Then all women report that they intend to have more children; that is, P(i = 1 | s) = 1 for all s. This very substantial divergence between intentions and choice probabilities is consistent with the hypothesis that women report rational-expectations predictions of their future fertility. By equation (5.13), the rational-expectations hypothesis implies only that P(γ = 1 | s) lies between .50 and 1.
Empirical Evidence from the NLS72
The NLS72 data offer an opportunity to illustrate the bounds just derived. The schooling/work intentions questions quoted at the beginning of the section were followed by behavior questions asked in the fall of 1974:
What were you doing the first week of October 1974?
These questions about behavior correspond closely, though not perfectly, to the intentions questions asked a year earlier.14
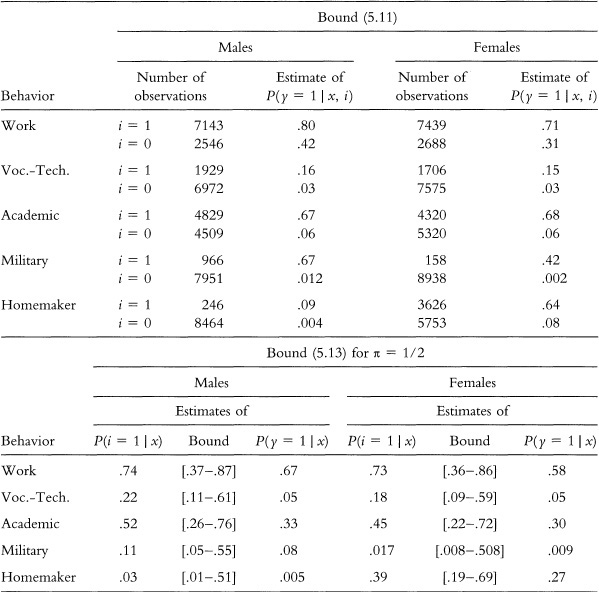
Table 5.2 presents empirical findings that condition on the respondent’s sex and on the assumption that respondents use the common threshold value π = 1/2. The quantities P(i = 1 | x), P(γ = 1 | x), and P(γ = 1 | x, i) are estimated by corresponding sample frequencies. For example, the estimate of P(work = 1 | x = male, i = 0) is based on the 2546 males who said they did not expect to work; the fraction of this group who reported working a year later was .42.
Inspection of the table shows that the male and female responses to the “work” and “academic” questions satisfy the bounds. So do the male responses to the “military” question and the female responses to the “homemaker” question. The female responses to the “military” question satisfy the bounds except for a small violation of bound (5.11) by those stating i = 1.
On the other hand, the responses of both sexes to the “voc.-tech.” question and the male responses to the “homemaker” question violate the bounds substantially. Respondents who say they expect to take voc.-tech. courses later do so only 16 or 15 percent of the time. Males who say they expect to be homemakers later report themselves as such only 9 percent of the time.
Probabilistic Intentions
The use of intentions data to predict behavior has been controversial. At least part of the controversy stems from the fact that researchers have expected too much correspondence between stated intentions and subsequent behavior. Social psychologists have written that intentions and behavior should coincide. Demographers have written that individual-level divergences between intentions and behavior should average out in the aggregate, so that (5.14) holds. In reality both premises are flawed. Intentions and behavior may diverge substantially, both at the individual level and in the aggregate, whenever behavior depends on events not yet realized at the time of the survey. This is so even if intentions data provide the best predictions of behavior that can be made given the information available when the survey is performed.
Table 5.2 Consistency of schooling-work behavior in October 1974 with intentions stated in fall 1973
Source: Manski (1990b), table 1.
Note: The number of observations is not the same across questions because some respondents did not answer some questions. For example, 9689 males (i.e., 7143 + 2546) answered the work intentions question while 8917 (i.e., 966 + 7951) answered the military question.
We have seen that binary intentions data have no predictive power in the absence of information about the threshold values π that respondents use in forming their responses. Even with π known, binary intentions data at most imply the bounds (5.11) and (5.13). It would seem that a superior survey approach would be to ask respondents for probabilistic assessments of their future behavior. For example, female respondents to the CPS could be asked:
Looking ahead, what is the percent chance that you will have any (more) children?
If expectations are rational, elicitation of probabilistic intentions reveals P(γ = 1 | s), which expresses all that can be said about future behavior given the information in s. Even if expectations are not rational, probabilistic intentions data may have greater predictive power than do binary data.
Juster (1966) not only proposed elicitation of probabilistic intentions but carried out an empirical study of probabilistic buying intentions. Market researchers have subsequently performed a variety of such studies (see Morrison, 1979; Urban and Hauser, 1980; and Jamieson and Bass, 1989). Psychologists studying judgment and decision making often elicit probabilistic predictions (see Wallsten and Budescu, 1983). Never-theless, the intentions questions posed on major surveys continue to be predominately like those on the CPS and NLS72.