6 RISK AND REWARD

(RATIONAL CHOICE AND EXPECTED UTILITY)

Everyone complains about his memory, and no one complains about his judgment.

—La Rochefoucauld

Some theories are unlovable. No one has much affection for the laws of thermodynamics, and generations of hopeful crackpots have sent patent offices their doomed designs for a perpetual motion machine. Ever since Darwin proposed the theory of natural selection, creationists have choked on the implication that humans descended from apes, and communitarians have looked for loopholes in its tenet that evolution is driven by competition.

One of the most hated theories of our time is known in different versions as rational choice, rational actor, expected utility, and Homo economicus.¹ This past Christmas season, CBS This Morning ran a heartwarming segment on a study that dropped thousands of money-filled wallets in cities across the world and found that most were returned, especially when they contained more money, reminding us that human beings are generous and honest after all. The grinch in the story? “Rationalist approaches to economics,” which supposedly predict that people live by the credo “Finders keepers, losers weepers.”²

What exactly is this mean-spirited theory? It says that when faced with a risky decision, rational actors ought to choose the option that maximizes their “expected utility,” namely the sum of its possible rewards weighted by their probabilities. Outside of economics and a few corners of political science, the theory is about as lovable as Ebenezer Scrooge. People interpret it as claiming that humans are, or should be, selfish psychopaths, or that they are uber-rational brainiacs who calculate probabilities and utilities before deciding whether to fall in love. Discoveries from the psychology lab showing that people seem to violate the theory have been touted as undermining the foundations of classical economics, and with it the rationale for market economies.³

In its original form, though, rational choice theory is a theorem of mathematics, considered quite beautiful by aficionados, with no direct implications for how members of our species think and choose. Many consider it to have provided the most rigorous characterization of rationality itself, a benchmark against which to measure human judgment. As we shall see, this can be contested—sometimes when people depart from the theory, it’s not clear whether the people are being irrational or the supposed standards of rationality are irrational. Either way, the theory shines a light on perplexing conundrums of rationality, and despite its provenance in pure math, it can be a source of profound life lessons.⁴

The theory of rational choice goes back to the dawn of probability theory and the famous argument by Blaise Pascal (1623–1662) on why you should believe in God: if you did and he doesn’t exist, you would just have wasted some prayers, whereas if you didn’t and he does exist, you would incur his eternal wrath. It was formalized in 1944 by the mathematician John von Neumann and the economist Oskar Morgenstern. Unlike the pope, von Neumann really might have been a space alien—his colleagues wondered about it because of his otherworldly intelligence. He also invented game theory (chapter 8), the digital computer, self-replicating machines, quantum logic, and key components of nuclear weapons, while making dozens of other breakthroughs in math, physics, and computer science.

Rational choice is not a psychological theory of how human beings choose, or a normative theory of what they ought to choose, but a theory of what makes choices consistent with the chooser’s values and each other. That ties it intimately to the concept of rationality, which is about making choices that are consistent with our goals. Romeo’s pursuit of Juliet is rational, and the iron filings’ pursuit of the magnet is not, because only Romeo chooses whichever path brings about his goal (chapter 2). At the other end of the scale, we call people “crazy” when they do things that are patently against their interests, like throwing away their money on things they don’t want or running naked into the freezing cold.

The beauty of the theory is that it takes off from a few easy-to-swallow axioms: broad requirements that apply to any decision maker we’d be willing to call “rational.” It then deduces how the decider would have to make decisions in order to stay true to those requirements. The axioms have been lumped and split in various ways; the version I’ll present here was formulated by the mathematician Leonard Savage and codified by the psychologists Reid Hastie and Robyn Dawes.⁵

A Theory of Rational Choice

The first axiom may be called Commensurability: for any options A and B, the decider prefers A, or prefers B, or is indifferent between them.⁶ This may sound vacuous—aren’t those just the logical possibilities?—but it requires the decider to commit to one of the three, even if it’s indifference. The decider, that is, never falls back on the excuse “You can’t compare apples and oranges.” We can interpret it as the requirement that a rational agent must care about things and prefer some to others. The same cannot be said for nonrational entities like rocks and vegetables.

The second axiom, Transitivity, is more interesting. When you compare options two at a time, if you prefer A to B, and B to C, then you must prefer A to C. It’s easy to see why this is a nonnegotiable requirement: anyone who violates it can be turned into a “money pump.” Suppose you prefer an Apple iPhone to a Samsung Galaxy but are saddled with a Galaxy. I will now sell you a sleek iPhone for $100 with the trade-in. Suppose you also prefer a Google Pixel to an iPhone. Great! You’d certainly trade in that crummy iPhone for the superior Pixel plus a premium of, say, $100. And suppose you prefer a Galaxy to a Pixel—that’s the intransitivity. You can see where this is going. For $100 plus a trade-in, I’ll sell you the Galaxy. You’d be right where you started, $300 poorer, and ready for another round of fleecing. Whatever you think rationality consists of, it certainly isn’t that.

The third is called Closure. With God playing dice and all that, choices are not always among certainties, like picking an ice cream flavor, but may include a collection of possibilities with different odds, like picking a lottery ticket. The axiom states that as long as the decider can consider A and B, that decider can also consider a lottery ticket that offers A with a certain probability, p, and B with the complement probability, 1 – p.

Within rational choice theory, although the outcome of a chancy option cannot be predicted, the probabilities are fixed, like in a casino. This is called risk, and may be distinguished from uncertainty, where the decider doesn’t even know the probabilities and all bets are off. In 2002, the US defense secretary Donald Rumsfeld famously explained the distinction: “There are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns—the ones we don’t know we don’t know.” The theory of rational choice is a theory of decision making with known unknowns: with risk, not necessarily uncertainty.

I’ll call the fourth axiom Consolidation.⁷ Life doesn’t just present us with lotteries; it presents us with lotteries whose prizes may themselves be lotteries. A chancy first date, if it goes well, can lead to a second date, which brings a whole new set of risks. This axiom simply says that a decider faced with a series of risky choices works out the overall risk according to the laws of probability explained in chapter 4. If the first lottery ticket has a one-in-ten chance of a payout, with the prize being a second ticket with a one-in-five chance of a payout, then the decider treats it as being exactly as desirable as a ticket with a one-in-fifty chance of the payout. (We’ll put aside whatever extra pleasure is taken in a second opportunity to watch the bouncing ping-pong balls or to scratch off the ticket coating.) This criterion for rationality seems obvious enough. As with the speed limit and gravity, so with probability theory: It’s not just a good idea. It’s the law.

The fifth axiom, Independence, is also interesting. If you prefer A to B, then you also prefer a lottery with A and C as the payouts to a lottery with B and C as the payouts (holding the odds constant). That is, adding a chance at getting C to both options should not change whether one is more desirable than the other. Another way of putting it is that how you frame the choices—how you present them in context—should not matter. A rose by any other name should smell just as sweet. A rational decider should focus on the choices themselves and not get sidelined by some distraction that accompanies them both.

Independence from Irrelevant Alternatives, as the generic version of Independence is called, is a requirement that shows up in many theories of rational choice.⁸ A simpler version says that if you prefer A to B when choosing between them, you should still prefer A to B when choosing among them and a third alternative, C. According to legend, the logician Sidney Morgenbesser (whom we met in chapter 3) was seated at a restaurant and offered a choice of apple pie or blueberry pie. Shortly after he chose apple, the waitress returned and said they also had cherry pie on the menu that day. As if waiting for the moment all his life, Morgenbesser said, “In that case, I’ll have blueberry.”⁹ If you find this funny, then you appreciate why Independence is a criterion for rationality.

The sixth is Consistency: if you prefer A to B, then you prefer a gamble in which you have some chance at getting A, your first choice, and otherwise get B, to the certainty of settling for B. Half a chance is better than none.

The last may be called Interchangeability: desirability and probability trade off.¹⁰ If the decider prefers A to B, and prefers B to C, there must be some probability that would make her indifferent between getting B for sure, her middle choice, and having a shot at getting either A, her top choice, or settling for C. To get a feel for this, imagine the probability starting high, with a 99 percent chance of getting A and only a 1 percent chance of getting C. Those odds make the gamble sound a lot better than settling for your second choice, B. Now consider the other extreme, a 1 percent chance of getting your first choice and a 99 percent chance of getting your last one. Then it’s the other way around: the sure mediocre option beats the near certainty of having to settle for the worst. Now imagine a sequence of probabilities from almost-certainly-A to almost-certainly-C. As the odds gradually shift, do you think you’d stick with the gamble up to a certain point, then be indifferent between gambling and settling for B, then switch to the sure B? If so, you agree that Interchangeability is rational.

Now here is the theorem’s payoff. To meet these criteria for rationality, the decider must assess the value of each outcome on a continuous scale of desirability, multiply by its probability, and add them up, yielding the “expected utility” of that option. (In this context, expected means “on average, in the long run,” not “anticipated,” and utility means “preferable by the lights of the decider,” not “useful” or “practical.”) The calculations need not be conscious or with numbers; they can be sensed and combined as analogue feelings. Then the decider should pick the option with the highest expected utility. That is guaranteed to make the decider rational by the seven criteria. A rational chooser is a utility maximizer, and vice versa.

To be concrete, consider a choice between games in a casino. In craps, the probability of rolling a “7” is 1 in 6, in which case you would win $4; otherwise you forfeit the $1 cost of playing. Suppose for now that every dollar is a unit of utility. Then the expected utility of betting on “7” in craps is (1/6 × $4) + (5/6 × –$1), or –$0.17. Compare that with roulette. In roulette, the probability of landing on “7” is 1 in 38, in which case you would win $35; otherwise you forfeit your $1. Its expected utility is (1/38 × $35) + (37/38 × –$1), or –$0.05. The expected utility of betting “7” in craps is lower than that in roulette, so no one would call you irrational for preferring roulette. (Of course, someone might call you irrational for gambling in the first place, since the expected value of both bets is negative, owing to the house’s take, so the more you play, the more you lose. But if you entered the casino in the first place, presumably you place some positive utility on the glamour of Monte Carlo and the frisson of suspense, which boosts the utility of both options into positive territory and leaves open only the choice of which to play.)

Games of chance make it easy to explain the theory of rational choice, because they provide exact numbers we can multiply and add. But everyday life presents us with countless choices that we intuitively evaluate in terms of their expected utilities. I’m in a convenience store and don’t remember whether there’s milk in the fridge; should I buy a quart? I suspect I’m out, and if that’s the case and I forgo the purchase, I’ll be really annoyed at having to eat my cereal dry tomorrow morning. On the other hand if there is milk at home and I do buy more, the worst that can happen is that it will spoil, but that’s unlikely, and even if it does, I’ll only be out a couple of bucks. So all in all I’m better off buying it. The theory of rational choice simply spells out the rationale behind this kind of reasoning.

How Useful Is Utility?

It’s tempting to think that the patterns of preferences identified in the axioms of rationality are about people’s subjective feelings of pleasure and desire. But technically speaking, the axioms treat the decider as a black box and consider only her patterns of picking one thing over another. The utility scale that pops out of the theory is a hypothetical entity that is reconstructed from the pattern of preferences and recommended as a way to keep those preferences consistent. The theory protects the decider from being turned into a money pump, a dessert flip-flopper, or some other kind of flibbertigibbet. This means the theory doesn’t so much tell us how to act in accord with our values as how to discover our values by observing how we act.

That lays to rest the first misconception of the theory of rational choice: that it portrays people as amoral hedonists or, worse, advises them to become one. Utility is not the same as self-interest; it’s whatever scale of value a rational decider consistently maximizes. If people make sacrifices for their children and friends, if they minister to the sick and give alms to the poor, if they return a wallet filled with money, that shows that love and charity and honesty go into their utility scale. The theory just offers advice on how not to squander them.

Of course, in pondering ourselves as decision makers, we don’t have to treat ourselves as black boxes. The hypothetical utility scale should correspond to our internal sensations of happiness, greed, lust, warm glow, and other passions. Things become interesting when we explore the relationship, starting with the most obvious object of desire, money. Whether or not money can buy happiness, it can buy utility, since people trade things for money, including charity. But the relationship is not linear; it’s concave. In jargon, it shows “diminishing marginal utility.”

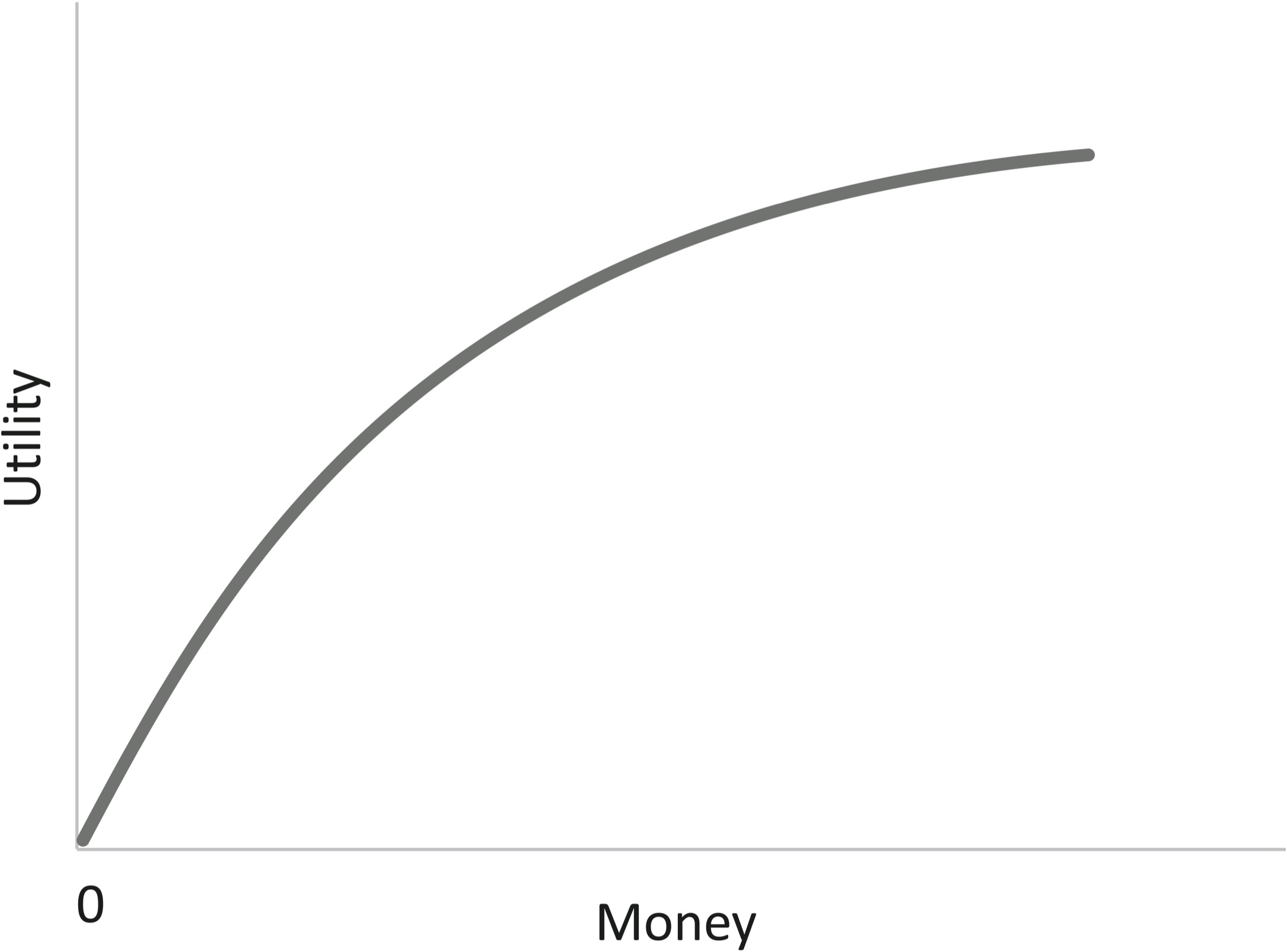
The psychological meaning is obvious: an extra hundred dollars increases the happiness of a poor person more than the happiness of a rich person.¹¹ (This is the moral argument for redistribution: transferring money from the rich to the poor increases the amount of happiness in the world, all things being equal.) In the theory of rational choice, this curve doesn’t actually come from the obvious source, namely asking people with different amounts of money how happy they are, but from looking at people’s preferences. Which would you rather have: a thousand dollars for sure, or a 50–50 chance of winning two thousand dollars? Their expected value is the same, but most people opt for the sure thing. This doesn’t mean they are flouting rational choice theory; it just means that utility is not the same as value in dollars. The utility of two thousand dollars is less than twice the utility of one thousand dollars. Fortunately for our understanding, people’s ratings of their satisfaction and their choice of gambles point to the same bent-over curve relating money and utility.

Economists equate a concave utility curve with being “risk-averse.” That’s a bit confusing, because the term does not refer to being a nervous Nellie as opposed to a daredevil, only to preferring a sure thing to a bet with the same expected payoff. Still, the concepts often coincide. People buy insurance for peace of mind, but so would an unfeeling rational decider with a concave utility curve. Paying the premium tugs her a bit leftward on the money scale, which lowers her happiness a bit, but if she had to replace her uninsured Tesla, her bank balance would lurch leftward, with a bigger plunge in happiness. Our rational chooser opts for the sure loss of the premium over a gamble with a bigger loss, even though the expected value of the sure loss (not to be confused with its expected utility) must be a bit lower for the insurance company to make a profit.

Unfortunately for the theory, by the same logic people should never gamble, buy a lottery ticket, start a company, or aspire to stardom rather than become a dentist. But of course some people do, a paradox that tied classical economists in knots. The human utility curve can’t be both concave, explaining why we avert risk with insurance, and convex, explaining why we seek risk by gambling. Perhaps we gamble for the thrill, just as we buy insurance for the peace of mind, but this appeal to emotions just pushes the paradox up a level: why did we evolve with the contradictory motives to jack ourselves up and calm ourselves down, paying for both privileges? Perhaps we’re irrational and that’s all there is to it. Perhaps the showgirls, spinning cherries, and other accoutrements of gambling are a form of entertainment that high rollers are willing to spend for. Or perhaps the curve has a second bend and shoots upward at the high end, making the expected utility of a jackpot higher than that of a mere increment in one’s bank balance. This could happen if people felt that the prize would vault them into a different social class and lifestyle: the life of a glamorous and carefree millionaire, not just a better-heeled member of the bourgeoisie. Many ads for state lotteries encourage that fantasy.

Though it’s easiest to think through the implications of the theory when the utility is reckoned in cash, the logic applies to anything of value we can place along a scale. This includes the public valuation of human life. The saying falsely attributed to Josef Stalin, “One death is a tragedy, a million deaths is a statistic,” gets the numbers wrong but captures the way we treat the moral cost of lives lost in a disaster like a war or pandemic. The curve bends over, like the one for the utility of money.¹² On a normal day, a terrorist attack or an incident of food poisoning with a dozen victims can get wall-to-wall coverage. But in the midst of a war or pandemic, a thousand lives lost in a day is taken in stride—even though each of those lives, unlike a diminishing dollar, was a real person, a sentient being who loved and was loved. In The Better Angels of Our Nature, I suggested that our morally misguided sense of the diminishing marginal utility of human lives is a reason why small wars can escalate into humanitarian catastrophes.¹³

Violating the Axioms: How Irrational?

You might think that the axioms of rational choice are so obvious that any normal person would respect them. In fact, people frequently cock a snook at them.

Let’s begin with Commensurability. It would seem impossible to flout: it’s just the requirement that you must prefer A to B, prefer B to A, or be indifferent between them. In chapter 2 we witnessed the act of rebellion, the taboo tradeoff.¹⁴ People treat certain things in life as sacrosanct and find the very thought of comparing them immoral. They feel that anyone who obeys the axiom is like Oscar Wilde’s “cynic”: a person who knows the price of everything and the value of nothing. How much should we spend to save an endangered species from extinction? To save the life of a little girl who fell down a well? Should we balance the budget by cutting funds for education, seniors, or the environment? A joke from another era begins with a man asking, “Would you sleep with me for a million dollars?”¹⁵ The idiom “Sophie’s choice” originated in William Styron’s harrowing novel, where it referred to the protagonist having to surrender one of her two children to be gassed in Auschwitz. We saw in chapter 2 how recoiling from the demand to compare sacred entities can be both rational, when it affirms our commitment to a relationship, and irrational, when we look away from painful choices but in fact make them capriciously and inconsistently.

A different family of violations involve a concept introduced by the psychologist Herbert Simon called bounded rationality.¹⁶ Theories of rational choice assume an angelic knower with perfect information and unlimited time and memory. For mortal deciders, uncertainty in the odds and payoffs, and the costs of obtaining and processing the information, have to be factored into the decision. It makes no sense to spend twenty minutes figuring out a shortcut that will save you ten minutes in travel time. The costs are by no means trifling. The world is a garden of forking paths, with every decision taking us into a situation in which new decisions confront us, exploding into a profusion of possibilities that could not possibly be tamed by the Consolidation axiom. Simon suggested that a flesh-and-blood decider rarely has the luxury of optimizing but instead must satisfice, a portmanteau of “satisfy” and “suffice,” namely settle for the first alternative that exceeds some standard that’s good enough. Given the costs of information, the perfect can be the enemy of the good.

Unfortunately, a decision rule that makes life simpler can violate the axioms, including Transitivity. Even Transitivity? Could I make a living by finding a human money pump and selling him the same things over and over, like Sylvester McMonkey McBean in Dr. Seuss’s The Sneetches, who repeatedly charged the Sneetches three dollars to affix a star to their bellies and ten dollars to have it removed? (“Then, when every last cent of their money was spent / The Fix-It-Up Chappie packed up. And he went.”) Though intransitivity is the epitome of irrationality, it can easily arise from two features of bounded rationality.

One is that we don’t do all the multiplications and additions necessary to melt down the attributes of an item into a glob of utility. Instead we may consider its attributes one by one, whittling down the choices by a process of elimination.¹⁷ In choosing a college, we might first rule out the ones without a lacrosse team, then the ones without a medical school, then the ones too far from home, and so on.

The other shortcut is that we may ignore a small difference in the values of one attribute when others seem more relevant. Savage asks us to consider a tourist who can’t decide between visiting Paris and Rome.¹⁸ Suppose instead she was given a choice between visiting Paris and visiting Paris plus receiving a dollar. Paris + $1 is unquestionably more desirable than Paris alone. But that does not mean that Paris + $1 is unquestionably more desirable than Rome! We have a kind of intransitivity: the tourist prefers A (Paris + $1) to B (Paris), and is indifferent between B and C (Rome), but does not prefer A to C. Savage’s example was rediscovered by a New Yorker cartoonist:

Michael Maslin/The New Yorker Collection/The Cartoon Bank

A decider who chooses by a process of elimination can fall into full-blown intransitivity.¹⁹ Tversky imagines three job candidates differing in their scores on an aptitude test and years of experience:

	Aptitude	Experience
Archer	200	6
Baker	300	4
Connor	400	2

A human resources manager compares them two at a time with this policy: If one scores more than 100 points higher in aptitude, choose that candidate; otherwise pick the one with more experience. The manager prefers Archer to Baker (more experience), Baker to Connor (more experience), and Connor to Archer (higher aptitude). When experimental participants are put in the manager’s shoes, many of them make intransitive sets of choices without realizing it.

So have behavioral economists been able to fund their research by using their participants as money pumps? Mostly not. People catch on, think twice about their choices, and don’t necessarily buy something just because they momentarily prefer it.²⁰ But without these double-takes from System 2, the vulnerability is real. In real life, the process of making decisions by comparing alternatives one aspect at a time can leave a decider open to irrationalities that we all recognize in ourselves. When deciding among more than two choices, we may be swayed by the last pair we looked at, or go around in circles as each alternative seems better than the other two in a different way.²¹

And people really can be turned into money pumps, at least for a while, by preferring A to B but putting a higher price on B.²² (You would sell them B, trade them A for it, buy back A at the lower price, and repeat.) How could anyone land in this crazy contradiction? It’s easy: when faced with two choices with the same expected value, people may prefer the one with the higher probability but pay more for the one with the higher payoff. (Concretely, consider two tickets to play roulette that have the same expected value, $3.85, but from different combinations of odds and payoffs. Ticket A gives you a 35/36 chance of winning $4 and a 1/36 chance of losing $1. Ticket B gives you an 11/36 chance of winning $16 and a 25/36 chance of losing $1.50.²³ Given the choice, people pick A. Asked what they would pay for each, they offer a higher price for B.) It’s barmy—when people think about a price, they glom onto the bigger number after the dollar sign and forget the odds—and the experimenter can act as an arbitrageur and pump money out of some of them. The bemused victims say, “I just can’t help it,” or “I know it’s silly and you’re taking advantage of me, but I really do prefer that one.”²⁴ After a few rounds, almost everyone wises up. Some of the churning in real financial markets may be stirred by naïve investors being swayed by risks at the expense of rewards or vice versa and arbitrageurs swooping in to exploit the inconsistencies.

What about the Independence from Irrelevant Alternatives, with its ditzy dependence on context and framing? The economist Maurice Allais uncovered the following paradox.²⁵ Which of these two tickets would you prefer?

Supercash:	100% chance of $1 million	Powerball:	10% chance of $2.5 million
			89% chance of $1 million

Though the expected value of the Powerball ticket is larger ($1.14 million), most people go for the sure thing, avoiding the 1 percent chance of ending up with nothing. That doesn’t violate the axioms; presumably their utility curve bends over, making them risk-averse. Now which of these two would you prefer?

Megabucks:

11% chance of $1 million

LottoUSA:

10% chance of $2.5 million

With this choice, people prefer LottoUSA, which tracks their expected values ($250,000 versus $110,000). Sounds reasonable, right? While pondering the first choice, the homunculus in your head is saying, “The Powerball lottery may have a bigger prize, but if you take it, there’s a chance you would walk away with nothing. You’d feel like an idiot, knowing you had blown a million dollars!” When looking at the second choice, it says, “Ten percent, eleven percent, what’s the difference? Either way, you have some chance at winning—might as well go for the bigger prize.”

Unfortunately for the theory of rational choice, the preferences violate the Independence axiom. To see the paradox, let’s carve the probabilities of the two left-hand choices into pieces, keeping everything the same except the way they’re presented:

Supercash:	10% chance of $1 million	Powerball:	10% chance of $2.5 million
	1% chance of $1 million		89% chance of $1 million
	89% chance of $1 million

Megabucks:

10% chance of $1 million

LottoUSA:

10% chance of $2.5 million

1% chance

of $1 million

We now see that the choice between Supercash and Powerball is just the choice between Megabucks and LottoUSA with an extra 89 percent chance of winning a million dollars tacked on to each. But that extra chance made you flip your pick. I added cherry pie to each ticket, and you switched from apple to blueberry. If you’re getting sick of reading about cash lotteries, Tversky and Kahneman offer a nonmonetary example.²⁶ Would you prefer a raffle ticket offering a 50 percent chance of a three-week tour of Europe, or a voucher giving you a one-week tour of England for sure? People go for the sure thing. Would you prefer a raffle ticket giving you a 5 percent chance of the three-week tour, or a ticket with a 10 percent chance of the England tour? Now people go for the longer tour.

Psychologically, it’s clear what’s going on. The difference between a probability of 0 and a probability of 1 percent isn’t just any old one-percentage-point gap; it’s the distinction between impossibility and possibility. Likewise, the difference between 99 percent and 100 percent is the distinction between possibility and certainty. Neither is commensurable with differences along the rest of the scale, like the difference between 10 percent and 11 percent. Possibility, however small, allows for hope looking forward, and regret looking back. Whether a choice driven by these emotions is “rational” depends on whether you think that emotions are natural responses we should respect, like eating and staying warm, or evolutionary nuisances our rational powers should override.

The emotions triggered by possibility and certainty add an extra ingredient to chance-laden choices like insurance and gambling which cannot be explained by the shapes of the utility curves. Tversky and Kahneman note that no one would buy probabilistic insurance, with premiums at a fraction of the cost but coverage only on certain days of the week, though they happily incur the same overall risk by insuring themselves against some hazards, like fires, but not others, like hurricanes.²⁷ They buy insurance for peace of mind—to give themselves one less thing to worry about. They would rather banish the fear of one kind of disaster from their anxiety closet than make their lives safer across the board. This may also explain societal decisions such as banning nuclear power, with its tiny risk of a disaster, rather than reducing the use of coal, with its daily drip of many more deaths. The American Superfund law calls for eliminating certain pollutants from the environment completely, though removing the last 10 percent may cost more than the first 90 percent. The US Supreme Court justice Stephen Breyer commented on litigation to force the cleanup of a toxic waste site: “The forty-thousand-page record of this ten-year effort indicated (and all the parties seemed to agree) that, without the extra expenditure, the waste dump was clean enough for children playing on the site to eat small amounts of dirt daily for 70 days each year without significant harm. . . . But there were no dirt-eating children playing in the area, for it was a swamp. . . . To spend $9.3 million to protect non-existent dirt-eating children is what I mean by the problem of ‘the last 10 percent.’ ”²⁸

I once asked a family member who bought a lottery ticket every week why he was throwing his money away. He explained to me, as if I were a slow child, “You can’t win if you don’t play.” His answer was not necessarily irrational: there may be a psychological advantage to holding a portfolio of prospects which includes the possibility of a windfall rather than single-mindedly maximizing expected utility, which guarantees it can’t happen. The logic is reinforced in a joke. A pious old man beseeches the Almighty. “O Lord, all my life I have obeyed your laws. I have kept the Sabbath. I have recited the prayers. I have been a good father and husband. I make only one request of you. I want to win the lottery.” The skies darken, a shaft of light penetrates the clouds, and a deep voice bellows, “I’ll see what I can do.” The man is heartened. A month passes, six months, a year, but fortune does not find him. In his despair he cries out again, “Lord Almighty, you know I am a pious man. I have beseeched you. Why have you forsaken me?” The skies darken, a shaft of light bursts forth, and a voice booms out, “Meet me halfway. Buy a ticket.”

It’s not just the framing of risks that can flip people’s choices; it’s also the framing of rewards. Suppose you have just been given $1,000. Now you must choose between getting another $500 for sure and flipping a coin that would give you another $1,000 if it lands heads. The expected value of the two options is the same ($500), but by now you have learned that most people are risk-averse and go for the sure thing. Now consider a variation. Suppose you have been given $2,000. You now must choose between giving back $500 and flipping a coin that would require you to give back $1,000 if it lands heads. Now most people flip the coin. But do the arithmetic: in terms of where you would end up, the choices are identical. The only difference is the starting point, which frames the outcomes as a “gain” with the first choice and a “loss” with the second. With this shift in framing, people’s risk aversion goes out the window: now they seek a risk if it offers the hope of avoiding a loss. Kahneman and Tversky conclude that people are not risk-averse across the board, though they are loss-averse: they seek risk if it may avoid a loss.²⁹

Once again, it’s not just in contrived gambles. Suppose you have been diagnosed with a life-threatening cancer and can have it treated either with surgery, which incurs some risk of dying on the operating table, or with radiation.³⁰ Experimental participants are told that out of every 100 patients who chose surgery, 90 survived the operation, 68 were alive after a year, and 34 were alive after five years. In contrast, out of every 100 who chose radiation, 100 survived the treatment, 77 were alive after a year, and 22 were alive after five years. Fewer than a fifth of the subjects opt for radiation—they go with the expected utility over the long term.

But now suppose the options are described differently. Out of every 100 patients who chose surgery, 10 died on the operating table, 32 died after a year, and 66 were dead within five years. Out of every 100 who chose radiation, none died during the treatment, 23 died after a year, and 78 died within five years. Now almost half choose radiation. They accept a greater overall chance of dying with the guarantee that they won’t be killed by the treatment right away. But the two pairs of options pose the same odds: all that changed was whether they were framed as the number who lived, perceived as a gain, or the number who died, perceived as a loss.

Once again, the violation of the axioms of rationality spills over from private choices into public policy. In an eerie premonition, forty years before Covid-19 Tversky and Kahneman asked people to “imagine that the U.S. is preparing for the outbreak of an unusual Asian disease.”³¹ I will update their example. The coronavirus, if left untreated, is expected to kill 600,000 people. Four vaccines have been developed, and only one can be distributed on a large scale. If Miraculon is chosen, 200,000 people will be saved. If Wonderine is chosen, there’s a ⅓ chance that 600,000 people will be saved and a ⅔ chance that no one will be saved. Most people are risk-averse and recommend Miraculon.

Now consider the other two. If Regenera is chosen, 400,000 people will die. If Preventavir is chosen, there’s a ⅓ chance that no one will die and a ⅔ chance that 600,000 people will die. By now you’ve developed an eye for trick questions in rationality experiments and have surely spotted that the two choices are identical, differing only in whether the effects are framed as gains (lives saved) or losses (deaths). But the flip in wording flips the preference: now a majority of people are risk-seeking and favor the Preventavir, which holds out the hope that the loss of life can be avoided entirely. It doesn’t take much imagination to see how these framings could be exploited to manipulate people, though they can be avoided with careful presentations of the data, such as always mentioning both the gains and the losses, or displaying them as graphs.³²

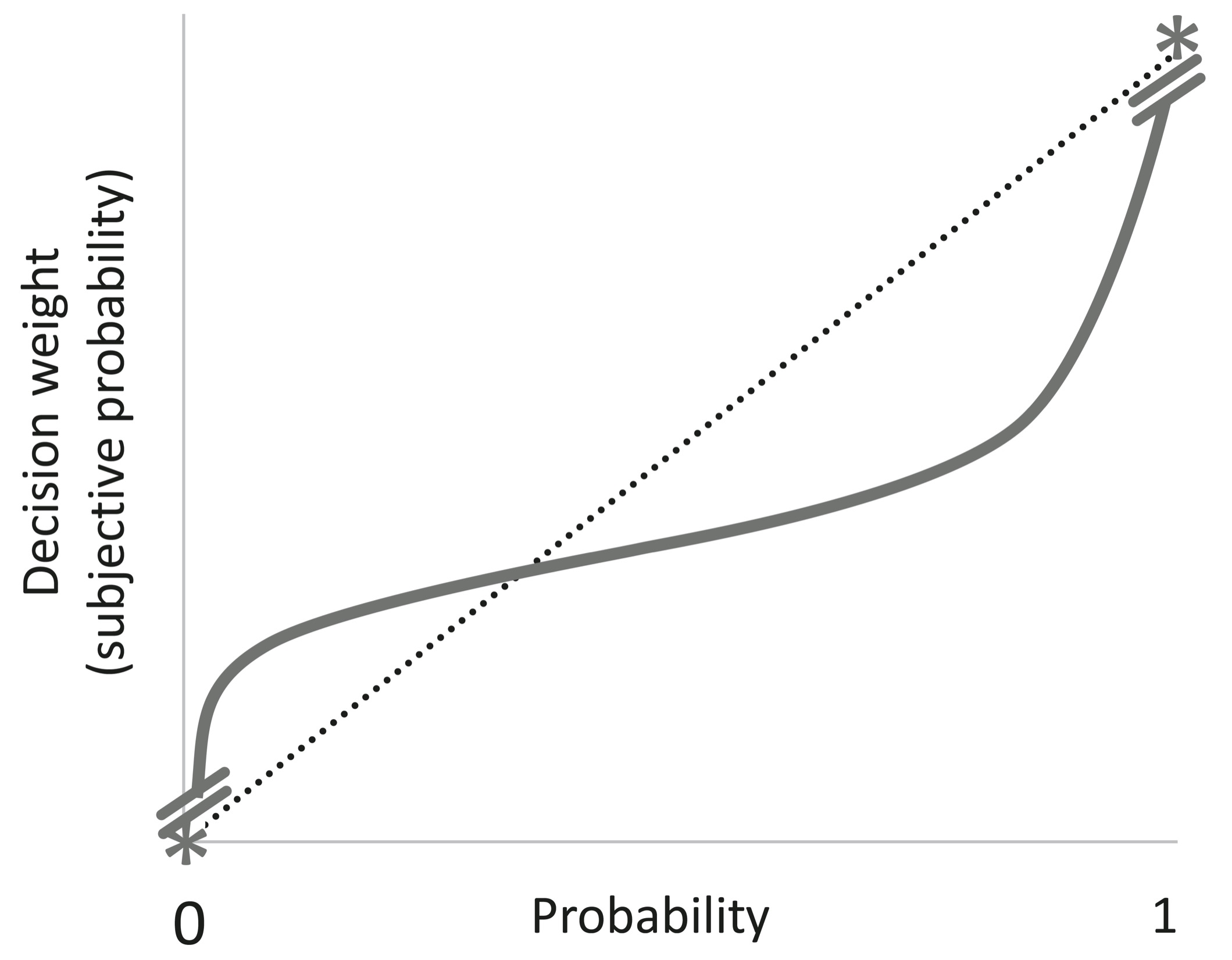
Kahneman and Tversky combined our misshapen sense of probability with our squirrelly sense of gains and losses into what they call Prospect theory.³³ It is an alternative to rational choice theory, intended to describe how people do choose rather than prescribe how they ought to choose. The graph below shows how our “decision weights,” the subjective sense of probability we apply to a choice, are related to objective probability.³⁴ The curve is steep near 0 and 1 (and with a discontinuity at the boundaries near those special values), more or less objective around .2, and flattish in the middle, where we don’t differentiate, say, .10 from .11.

A second graph displays our subjective value.³⁵ Its horizontal axis is centered at a movable baseline, usually the status quo, rather than at 0. The axis is demarcated not in absolute dollars, lives, or other valued commodities but in relative gains or losses with respect to that baseline. Both gains and losses are concave—each additional unit gained or lost counts for less than the ones already incurred—but the slope is steeper on the downside; a loss is more than twice as painful as the equivalent gain is pleasurable.

Of course, merely plotting phenomena as curves does not explain them. But we can make sense of these violations of the rational axioms. Certainty and impossibility are epistemologically very different from very high and very low probabilities. That’s why, in this book, logic is in a separate chapter from probability theory. (“P or Q; not P; therefore, Q” is not just a statement with a very high probability; it’s a logical truth.) It’s why patent officers send back applications for perpetual motion machines unopened rather than taking a chance that some genius has solved our energy problems once and for all. Benjamin Franklin was correct in at least the first half of his statement that nothing is certain but death and taxes. Intermediate probabilities, in contrast, are matters of conjecture, at least outside casinos. They are estimates with margins of error, sometimes large ones. In the real world it’s not foolish to treat the difference between a probability of .10 and a probability of .11 with a grain of salt.

The asymmetry between gains and losses, too, becomes more explicable when we descend from mathematics to real life. Our existence depends on a precarious bubble of improbabilities, with pain and death just a misstep away. As Tversky once asked me when we were colleagues, “How many things could happen to you today that could make you much better off? How many things could happen to you today that could make you much worse off? The second list is bottomless.” It stands to reason that we are more vigilant about what we have to lose, and take chances to avoid precipitous plunges in well-being.³⁶ And at the negative pole, death is not just something that really, really sucks. It’s game over, with no chance to play again, a singularity that makes all calculations of utility moot.

That is also why people can violate yet another axiom, Interchangeability. If I prefer a beer to a dollar, and a dollar to death, that does not mean that, with the right odds, I’d pay a dollar to bet my life for a beer.

Or does it?

Rational Choices after All?

In cognitive science and behavioral economics, showing all the ways in which people flout the axioms of rational choice has become something of a sport. (And not just a sport: five Nobel Prizes have gone to discoverers of the violations.)³⁷ Part of the fun comes from showing how irrational humans are, the rest from showing what bad psychologists the classical economists and decision theorists are. Gigerenzer loves to tell a true story about a conversation between two decision theorists, one of whom was agonizing over whether to take an enticing job offer at another university.³⁸ His colleague said, “Why don’t you write down the utilities of staying where you are versus taking the job, multiply them by their probabilities, and choose the higher of the two? After all, that’s what you advise in your professional work.” The first one snapped, “Come on, this is serious!”

But von Neumann and Morgenstern may deserve the last laugh. All those taboos, bounds, intransitivities, flip-flops, regrets, aversions, and framings merely show that people flout the axioms, not that they ought to. To be sure, in some cases, like the sacredness of our relationships and the awesomeness of death, we really may be better off not doing the sums prescribed by the theory. But we do always want to keep our choices consistent with our values. That’s all that the theory of expected utility can deliver, and it’s a consistency we should not take for granted. We call our decisions foolish when they subvert our values and wise when they affirm them. We have already seen that some breaches of the axioms truly are foolhardy, like avoiding tough societal tradeoffs, chasing zero risk, and being manipulated by a choice of words. I suspect there are countless decisions in life where if we did multiply the risks by the rewards we would choose more wisely.

When you buy a gadget, should you also buy the extended warranty pushed by the salesperson? About a third of Americans do, forking over $40 billion a year. But does it really make sense to take out a health insurance policy on your toaster? The stakes are smaller than insurance on a car or house, where the financial loss would have an impact on your well-being. If consumers thought even crudely about the expected value, they’d notice that an extended warranty can cost almost a quarter of the price of the product, meaning that it would pay off only if the product had more than a 1 in 4 chance of breaking. A glance at Consumer Reports would then show that modern appliances are nowhere near that flimsy: fewer than 7 percent of televisions, for example, need any kind of repair.³⁹ Or consider deductibles on home insurance. Should you pay an extra $100 a year to reduce your out-of-pocket expense in the event of a claim from $1,000 to $500? Many people do it, but it makes sense only if you expect to make a claim every five years. The average claim rate for homeowners insurance is in fact around once every twenty years, which means that the people are paying $100 for $25 in expected value (5 percent of $500).⁴⁰

Weighing risks and rewards can, with far greater consequences, also inform medical choices. Doctors and patients alike are apt to think in terms of propensities: cancer screening is good because it can detect cancers, and cancer surgery is good because it can remove them. But thinking about costs and benefits weighted by their probabilities can flip good to bad. For every thousand women who undergo annual ultrasound exams for ovarian cancer, 6 are correctly diagnosed with the disease, compared with 5 in a thousand unscreened women—and the number of deaths in the two groups is the same, 3. So much for the benefits. What about the costs? Out of the thousand who are screened, another 94 get terrifying false alarms, 31 of whom suffer unnecessary removal of their ovaries, of whom 5 have serious complications to boot. The number of false alarms and unnecessary surgeries among women who are not screened, of course, is zero. It doesn’t take a lot of math to show that the expected utility of ovarian cancer screening is negative.⁴¹ The same is true for men when it comes to screening for prostate cancer with the prostate-specific antigen test (I opt out). These are easy cases; we’ll take a deeper dive into how to compare the costs and benefits of hits and false alarms in the next chapter.

Even when exact numbers are unavailable, there is wisdom to be had in mentally multiplying probabilities by outcomes. How many people have ruined their lives by taking a gamble with a large chance at a small gain and a small chance at a catastrophic loss—cutting a legal corner for an extra bit of money they didn’t need, risking their reputation and tranquility for a meaningless fling? Switching from losses to gains, how many lonely singles forgo the small chance of a lifetime of happiness with a soul mate because they think only of the large chance of a tedious coffee with a bore?

As for betting your life: Have you ever saved a minute on the road by driving over the speed limit, or indulged your impatience by checking your new texts while crossing the street? If you weighed the benefits against the chance of an accident multiplied by the price you put on your life, which way would it go? And if you don’t think this way, can you call yourself rational?