7.3 Programming with Arrays
Never Trust to General Impressions, my Boy, but Concentrate Yourself Upon Details.
SIR ARTHUR CONAN DOYLE, A Case of Identity (Sherlock Holmes)
In this section we discuss partially filled arrays and give a brief introduction to sorting and searching of arrays. This section includes no new material about the C++ language, but does include more practice with C++ array parameters.
Partially Filled Arrays
Often the exact size needed for an array is not known when a program is written, or the size may vary from one run of the program to another. One common and easy way to handle this situation is to declare the array to be of the largest size the program could possibly need. The program is then free to use as much or as little of the array as is needed.
Partially filled arrays require some care. The program must keep track of how much of the array is used and must not reference any indexed variable that has not been given a value. The program in Display 7.9 illustrates this point. The program reads in a list of golf scores and shows how much each score differs from the average. This program will work for lists as short as one score, as long as ten scores, and for any length in between. The scores are stored in the array score, which has ten indexed variables, but the program uses only as much of the array as it needs. The variable numberUsed keeps track of how many elements are stored in the array. The elements (that is, the scores) are stored in positions score[0] through score[numberUsed − 1].
Display 7.9 Partially Filled Array
1//Shows the difference between each of a list of golf scores and their average.2 #include <iostream> 3const intMAX_NUMBER_SCORES = 10; 4voidfillArray(inta[],intsize,int& numberUsed); 5//Precondition: size is the declared size of the array a.6//Postcondition: numberUsed is the number of values stored in a.7//a[0] through a[numberUsed − 1] have been filled with8 //nonnegative integers read from the keyboard. 9doublecomputeAverage(const inta[],intnumberUsed); 10//Precondition: a[0] through a[numberUsed − 1] have values; numberUsed> 0.11//Returns the average of numbers a[0] through a[numberUsed − 1].12voidshowDifference(const inta[],intnumberUsed); 13//Precondition: The first numberUsed indexed variables of a have values.14//Postcondition: Gives screen output showing how much each of the first15//numberUsed elements of a differs from their average.16intmain( ) 17 { 18using namespacestd; 19intscore[MAX_NUMBER_SCORES], numberUsed; 20 cout << "This program reads golf scores and shows\n" 21 << "how much each differs from the average.\n"; 22 23 cout << "Enter golf scores:\n"; 24 fillArray(score, MAX_NUMBER_SCORES, numberUsed); 25 showDifference(score, numberUsed); 26return0; 27 } 28//Uses iostream:29voidfillArray(inta[],intsize,int&numberUsed) 30 { 31using namespacestd; 32 cout << "Enter up to " << size << " nonnegative whole numbers.\n" 33 << "Mark the end of the list with a negative number.\n"; 34intnext, index = 0; 35 cin >> next; 36while((next >= 0) && (index < size)) 37 { 38 a[index] = next; 39 index++; 40 cin >>next;41 } 42 numberUsed = index; 43 } 44doublecomputeAverage(const inta[],intnumberUsed) 45 { 46doubletotal = 0; 47for(intindex = 0; index < numberUsed; index++) 48 total = total + a[index]; 49if(numberUsed> 0) 50 { 51return(total/numberUsed); 52 } 53 else 54 { 55using namespacestd; 56 cout << "ERROR: number of elements is 0 in computeAverage.\n" 57<< "computeAveragereturns 0.\n"; 58return0; 59 } 60 } 61voidshowDifference(const inta[],intnumberUsed) 62 { 63using namespacestd; 64doubleaverage = computeAverage(a, numberUsed); 65 cout << "Average of the " << numberUsed 66 << " scores = " << average << endl 67 << "The scores are:\n"; 68for(intindex = 0; index < numberUsed; index++) 69 cout << a[index] << " differs from average by " 70 << (a[index] − average) << endl; 71 }
Sample Dialogue
This program reads golf scores and shows
how much each differs from the average.
Enter golf scores:
Enter up to 10 nonnegative whole numbers.
Mark the end of the list with a negative number.
69 74 68 −1
Average of the 3 scores = 70.3333
The scores are:
69 differs from average by −1.33333
74 differs from average by 3.66667
68 differs from average by −2.33333The details are very similar to what they would be if numberUsed were the declared size of the array and the entire array were used. In particular, the variable numberUsed usually must be an argument to any function that manipulates the partially filled array. Since the argument numberUsed (when used properly) can often ensure that the function will not reference an illegal array index, this sometimes (but not always) eliminates the need for an argument that gives the declared size of the array. For example, the functions showDifference and computeAverage use the argument numberUsed to ensure that only legal array indexes are used. However, the function fillArray needs to know the maximum declared size for the array so that it does not overfill the array.
Programming Tip Do Not Skimp on Formal Parameters
Notice the function fillArray in Display 7.9. When fillArray is called, the declared array size MAX_NUMBER_SCORES is given as one of the arguments, as shown in the following function call from Display 7.9:
fillArray(score, MAX_NUMBER_SCORES, numberUsed);You might protest that MAX_NUMBER_SCORES is a globally defined constant and so could be used in the definition of fillArray without the need to make it an argument. You would be correct, and if we did not use fillArray in any program other than the one in Display 7.9, we could get by without making MAX_NUMBER_SCORES an argument to fillArray. However, fillArray is a generally useful function that you may want to use in several different programs. We do in fact also use the function fillArray in the program in Display 7.10, discussed in the next subsection. In the program in Display 7.10, the argument for the declared array size is a different named global constant. If we had written the global constant MAX_NUMBER_SCORES into the body of the function fillArray, we would not have been able to reuse the function in the program in Display 7.10.
Programming Example Searching an Array
A common programming task is to search an array for a given value. For example, the array may contain the student numbers for all students in a given course. To tell whether a particular student is enrolled, the array is searched to see if it contains the student’s number. The program in Display 7.10 fills an array and then searches the array for values specified by the user. A real application program would be much more elaborate, but this shows all the essentials of the sequential search algorithm. The sequential search algorithm is the most straightforward searching algorithm you could imagine: The program looks at the array elements in the order first to last to see if the target number is equal to any of the array elements.
In Display 7.10, the function search is used to search the array. When searching an array, you often want to know more than simply whether or not the target value is in the array. If the target value is in the array, you often want to know the index of the indexed variable holding that target value, since the index may serve as a guide to some additional information about the target value. Therefore, we designed the function search to return an index giving the location of the target value in the array, provided the target value is, in fact, in the array. If the target value is not in the array, search returns −1. Let’s look at the function search in a little more detail.
The function search uses a while loop to check the array elements one after the other to see whether any of them equals the target value. The variable found is used as a flag to record whether or not the target element has been found. If the target element is found in the array, found is set to true, which in turn ends the while loop.
Display 7.10 Searching an Array
1 //Searches a partially filled array of nonnegative integers.
2 #include <iostream>
3 const int DECLARED_SIZE = 20;
4 void fillArray(int a[], int size, int& numberUsed);
5 //Precondition: size is the declared size of the array a.
6 //Postcondition: numberUsed is the number of values stored in a.
7 //a[0] through a[numberUsed − 1] have been filled with
8 //nonnegative integers read from the keyboard.
9 int search(const int a[], int numberUsed, int target);
10 //Precondition: numberUsed is <= the declared size of a.
11 //Also, a[0] through a[numberUsed − 1] have values.
12 //Returns the first index such that a[index] == target,
13 //provided there is such an index; otherwise, returns −1.
14 int main( )
15 {
16 using namespace std;
17 int arr[DECLARED_SIZE], listSize, target;
18 fillArray(arr, DECLARED_SIZE, listSize);
19 char ans;
20 int result;
21 do
22 {
23 cout << "Enter a number to search for: ";
24 cin >> target;
25 result = search(arr, listSize, target);
26 if (result == −1)
27 cout << target << " is not on the list.\n";
28 else
29 cout << target << " is stored in array position "
30 << result << endl
31 << "(Remember: The first position is 0.)\n";
32 cout << "Search again?(y/n followed by Return): ";
33 cin >> ans;
34 } while ((ans != 'n') && (ans != 'N'));
35 cout << "End of program.\n";
36 return 0;
37 }
38 //Uses iostream:
39 void fillArray(int a[], int size, int& numberUsed)
<The rest of the definition of fillArray is given in Display 7.9.>
40
41 int search(const int a[], int numberUsed, int target)
42 {
43
44 int index = 0;
45 bool found = false;
46 while ((!found) && (index < numberUsed))
47 if (target == a[index])
48 found = true;
49 else
50 index++;
51
52 if (found)
53 return index;
54 else
55 return −1;
56 }
Sample Dialogue
Enter up to 20 nonnegative whole numbers. Mark the end of the list with a negative number. 10 20 30 40 50 60 70 80 −1 Enter a number to search for:10 10 is stored in array position 0. (Remember: The first position is 0.) Search again?(y/n followed by Return): y Enter a number to search for: 40 40 is stored in array position 3. (Remember: The first position is 0.) Search again?(y/n followed by Return): y Enter a number to search for: 42 42 is not on the list. Search again?(y/n followed by Return): n End of program.
Even if we used fillArray in only one program, it can still be a good idea to make the declared array size an argument to fillArray. Displaying the declared size of the array as an argument reminds us that the function needs this information in a critically important way.
Programming Example Sorting an Array
One of the most widely encountered programming tasks, and certainly the most thoroughly studied, is sorting a list of values, such as a list of sales figures that must be sorted from lowest to highest or from highest to lowest, or a list of words that must be sorted into alphabetical order. In this section we describe a function called sort that sorts a partially filled array of numbers so that they are ordered from smallest to largest.
The procedure sort has one array parameter a. The array a will be partially filled, so there is an additional formal parameter called numberUsed, which tells how many array positions are used. Thus, the declaration and precondition for the function sort is
voidsort(inta[],intnumberUsed);//Precondition: numberUsed <= declared size of the array a. //Array elements a[0] through a[numberUsed − 1] have values.
The function sort rearranges the elements in array a so that after the function call is completed the elements are sorted as follows:
a[0] ≤ a[1] ≤ a[2] ≤ ... ≤ a[numberUsed − 1]The algorithm we use to do the sorting is called selection sort. It is one of the easiest of the sorting algorithms to understand.
One way to design an algorithm is to rely on the definition of the problem. In this case the problem is to sort an array a from smallest to largest. That means rearranging the values so that a[0] is the smallest, a[1] the next smallest, and so forth. That definition yields an outline for the selection sort algorithm:
for(intindex = 0; index < numberUsed; index++)
Place the indexth smallest element in a[index]
There are many ways to realize this general approach. The details could be developed using two arrays and copying the elements from one array to the other in sorted order, but one array should be both adequate and economical. Therefore, the function sort uses only the one array containing the values to be sorted. The function sort rearranges the values in the array a by interchanging pairs of values. Let us go through a concrete example so that you can see how the algorithm works.
Consider the array shown in Display 7.11. The algorithm will place the smallest value in a[0]. The smallest value is the value in a[3]. So the algorithm interchanges the values of a[0] and a[3]. The algorithm then looks for the next smallest element. The value in a[0] is now the smallest element and so the next smallest element is the smallest of the remaining elements a[1], a[2], a[3], . . ., a[9]. In the example in Display 7.11, the next smallest element is in a[5], so the algorithm interchanges the values of a[1] and a[5]. This positioning of the second smallest element is illustrated in the fourth and fifth array pictures in Display 7.11. The algorithm then positions the third smallest element, and so forth.
Display 7.11 Selection Sort
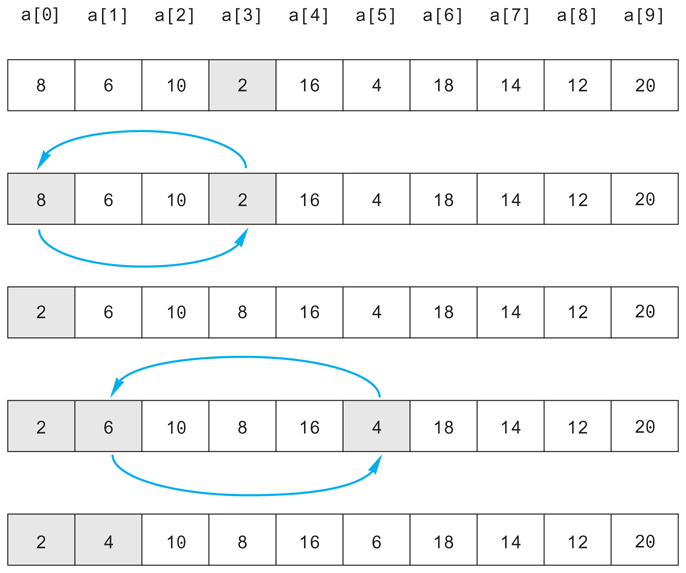
As the sorting proceeds, the beginning array elements are set equal to the correct sorted values. The sorted portion of the array grows by adding elements one after the other from the elements in the unsorted end of the array. Notice that the algorithm need not do anything with the value in the last indexed variable, a[9]. That is because once the other elements are positioned correctly, a[9] must also have the correct value. After all, the correct value for a[9] is the smallest value left to be moved, and the only value left to be moved is the value that is already in a[9].
The definition of the function sort, included in a demonstration program, is given in Display 7.12. sort uses the function indexOfSmallest to find the index of the smallest element in the unsorted end of the array, and then it does an interchange to move this element down into the sorted part of the array.
The function swapValues, shown in Display 7.12, is used to interchange the values of indexed variables. For example, the following call will interchange the values of a[0] and a[3]:
swapValues(a[0], a[3]);The function swapValues was explained in Chapter 5.
Display 7.12 Sorting an Array
1 //Tests the procedure sort.
2 #include <iostream>
3 void fillArray(int a[], int size, int& numberUsed);
4 //Precondition: size is the declared size of the array a.
5 //Postcondition: numberUsed is the number of values stored in a.
6 //a[0] through a[numberUsed − 1] have been filled with
7 //nonnegative integers read from the keyboard.
8 void sort(int a[], int numberUsed);
9 //Precondition: numberUsed <= declared size of the array a.
10 //The array elements a[0] through a[numberUsed − 1] have values.
11 //Postcondition: The values of a[0] through a[numberUsed − 1] have
12 //been rearranged so that a[0] <= a[1] <= ... <= a[numberUsed − 1].
13 void swapValues(int &v1, int &v2);
14 //Interchanges the values of v1 and v2.
15 int indexOfSmallest(const int a[], int startIndex, int numberUsed);
16 //Precondition: 0 <= startIndex < numberUsed. Referenced array elements have
17 //values.
18 //Returns the index i such that a[i] is the smallest of the values
19 //a[startIndex], a[startIndex + 1], ..., a[numberUsed − 1].
20 int main( )
21 {
22 using namespace std;
23 cout << "This program sorts numbers from lowest to highest.\n";
24 int sampleArray[10], numberUsed;
25 fillArray(sampleArray, 10, numberUsed);
26 sort(sampleArray, numberUsed);
27 cout << "In sorted order the numbers are:\n";
28 for (int index = 0; index < numberUsed; index++)
29 cout << sampleArray[index] << " ";
30 cout << endl;
31 return 0;
32 }
33 //Uses iostream:
34 void fillArray(int a[], int size, int& numberUsed)
<The rest of the definition of fillArray is given in Display 7.9.>
35 void sort(int a[], int numberUsed)
36 {
37 int indexOfNextSmallest;
38 for (int index = 0; index < numberUsed − 1; index++)
39 {//Place the correct value in a[index]:
40 indexOfNextSmallest =
41 indexOfSmallest(a, index, numberUsed);
42 swapValues(a[index], a[indexOfNextSmallest]);
43 //a[0] <= a[1] <=...<= a[index] are the smallest of the original array
44 //elements. The rest of the elements are in the remaining positions.
45 }
46 }
47
48 void swapValues(int& v1, int& v2)
49 {
50 int temp;
51 temp = v1;
52 v1 = v2;
53 v2 = temp;
54 }
55
56 int indexOfSmallest(const int a[], int startIndex, int numberUsed)
57 {
58 int min = a[startIndex],
59 indexOfMin = startIndex;
60 for (int index = startIndex + 1; index < numberUsed; index++)
61 if (a[index] < min)
62 {
63 min = a[index];
64 indexOfMin = index;
65 //min is the smallest of a[startIndex] through a[index]
66 }
67
68 return indexOfMin;
69 }Sample Dialogue
This program sorts numbers from lowest to highest.
Enter up to 10 nonnegative whole numbers.
Mark the end of the list with a negative number.
80 30 50 70 60 90 20 30 40 −1
In sorted order the numbers are:
20 30 30 40 50 60 70 80 90Programming Example Bubble Sort
The selection sort algorithm that we just described is not the only way to sort an array. In fact, computer scientists have devised scores of sorting algorithms! Some of these algorithms are more efficient than others and some work only for particular types of data. Bubble sort is a simple and general sorting algorithm that is similar to selection sort.
If we use bubble sort to sort an array in ascending order, then the largest value is successively “bubbled” toward the end of the array. For example, if we start with an unsorted array consisting of the following integers:
Initial array: {3, 10, 9, 2, 5}
Then after the first pass we will have moved the largest value, 10, to the end of the array:
After first pass: {3, 9, 2, 5, 10}
The second pass will move the second largest value, 9, to the second to last index of the array:
After second pass: {3, 2, 5, 9, 10}
The third pass will move the third largest value, 5, to the third to last index of the array (where it already is):
After third pass: {2, 3, 5, 9, 10}
The fourth pass will move the fourth largest value, 3, to the fourth to last index of the array (where it already is):
After fourth pass: {2, 3, 5, 9, 10}
At this point the algorithm is done. The remaining number at the beginning of the array doesn’t need to be examined since it is the only number left and must be the smallest. To design a program based on bubble sort note that we are placing the largest item at index length-1, the second largest item at length-2, the next at length-3, etc. This corresponds to a loop that starts at index length-1 of the array and counts down to index 1 of the array. We don’t need to include index 0 since that will contain the smallest element. One way to implement the loop is with the following code, where variable i corresponds to the target index:
for(inti = length-1; i > 0; i−−)
The “bubble” part of bubble sort happens inside each iteration of this loop. The bubble step consists of another loop that moves the largest number toward the index i in the array. First, the largest number between index 0 and index i will be bubbled up to index i. We start the bubbling procedure by comparing the number at index 0 with the number at index 1. If the number at index 0 is larger than the number at index 1 then the values are swapped so we end up with the largest number at index 1. If the number at index 0 is less than or equal to the number at index 1 then nothing happens. Starting with the following unsorted array:
Initial array: {3, 10, 9, 2, 5}
Then the first step of the bubbling procedure will compare 3 to 10. Since 10 > 3 nothing happens and the end result is the number 10 is at index 1:
After step 1: {3, 10, 9, 2, 5}
The procedure is repeated for successively larger values until we reach i. The second step will compare the numbers at index 1 and 2, which is values 10 and 9. Since 10 is larger than 9 we swap the numbers resulting in the following:
After step 2: {3, 9, 10, 2, 5}
The process is repeated two more times:
After step 3: {3, 9, 2, 10, 5}
After step 4: {3, 9, 2, 5, 10}
This ends the first iteration of the bubble sort algorithm. We have bubbled the largest number to the end of the array. The next iteration would bubble the second largest number to the second to last position, and so forth, where variable i represents the target index for the bubbled number. If we use variable j to reference the index of the bubbled item then our loop code looks like this:
for(inti = length-1; i > 0; i−−)for(intj = 0; j < i; j++)
Inside the loop we must compare the items at index j and index j+1. The largest should be moved into index j+1. The completed algorithm is shown below and a complete example in Display 7.13.
for(inti = length-1; i > 0; i−−)for(intj = 0; j < i; j++)if(arr[j] > arr[j+1]) {inttemp = arr[j+1]; arr[j+1] = arr[j]; arr[j] = temp; }
Display 7.13 Bubble Sort Program
1 //Display 7.13 Bubble Sort Program 2 //Sorts an array of integers using Bubble Sort. 3 #include <iostream> 4 5voidbubblesort(intarr[],intlength); 6 //Precondition: length <= declared size of the array arr. 7 //The array elements arr[0] through a[length − 1] have values. 8 //Postcondition: The values of arr[0] through arr[length − 1] have 9 //been rearranged so that arr[0] <= a[1] <= <= arr[length − 1]. 10 11intmain() 12 { 13using namespacestd; 14inta[] = {3, 10, 9, 2, 5, 1}; 15 16 bubblesort(a, 6); 17for(inti=0; i<6; i++) 18 { 19 cout << a[i] << " "; 20 } 21 cout << endl; 22 return 0; 23 } 24 25voidbubblesort(intarr[],intlength) 26 { 27 // Bubble largest number toward the right 28for(inti = length-1; i > 0; i−−) 29for(intj = 0; j < i; j++) 30if(arr[j] > arr[j+1]) 31 { 32 // Swap the numbers 33inttemp = arr[j+1]; 34 arr[j+1] = arr[j]; 35 arr[j] = temp; 36 } 37 }
Sample Dialogue
1 2 3 5 9 10
Self-Test Exercises
Write a program that will read up to ten nonnegative integers into an array called
numberArrayand then write the integers back to the screen. For this exercise you need not use any functions. This is just a toy program and can be very minimal.Write a program that will read up to ten letters into an array and write the letters back to the screen in the reverse order. For example, if the input is
abcd.then the output should bedcbaUse a period as a sentinel value to mark the end of the input. Call the array
letterBox. For this exercise you need not use any functions. This is just a toy program and can be very minimal.Following is the declaration for an alternative version of the function search defined in Display 7.12. In order to use this alternative version of the search function, we would need to rewrite the program slightly, but for this exercise all you need to do is to write the function definition for this alternative version of
search.boolsearch(const inta[],intnumberUsed,inttarget,int& where);//Precondition: numberUsed is <= the declared size of the //array a; a[0] through a[numberUsed − 1] have values. //Postcondition: If target is one of the elements a[0] //through a[numberUsed − 1], then this function returns //true and sets the value of where so that a[where] == //target; otherwise this function returns false and the //value of where is unchanged.