14.2 Recursive Functions For Values

To iterate is human, to recurse divine.

ANONYMOUS

General Form for a Recursive Function That Returns a Value

The recursive functions you have seen thus far are all void functions, but recursion is not limited to void functions. A recursive function can return a value of any type. The technique for designing recursive functions that return a value is basically the same as for void functions. An outline for a successful recursive function definition that returns a value is as follows.

One or more cases in which the value returned is computed in terms of calls to the same function (that is, using recursive calls). As was the case with void functions, the arguments for the recursive calls should intuitively be “smaller.”
One or more cases in which the value returned is computed without the use of any recursive calls. These cases without any recursive calls are called base cases or stopping cases (just as they were with void functions).

This technique is illustrated in the next Programming Example.

Programming Example Another Powers Function

In Chapter 4 we introduced the predefined function that computes powers. For example, pow(2.0,3.0) returns 2.0^3.0, so the following sets the variable x equal to 8.0:

double x = pow(2.0, 3.0);

The function pow takes two arguments of type double and returns a value of type double. Display 14.3 contains a recursive definition for a function that is similar but that works with the type int rather than double. This new function is called power. For example, the following will set the value of y equal to 8, since 2³ is 8:

int y = power(2, 3);

Display 14.3 The Recursive Function `power`

 1    //Program to demonstrate the recursive function power.
 2    #include <iostream>
 3    #include <cstdlib>
 4    using namespace std;
 5    int power(int x, int n);
 6    //Precondition: n > = 0.
 7    //Returns x to the power n.
 8    int main( )
 9    {
10        for (int n = 0; n < 4; n++)
11            cout << "3 to the power " << n
12                 << " is " << power(3, n) << endl;
13        return 0;
14    }
15    //uses iostream and cstdlib:
16    int power(int x, int n)
17    {
18        if (n < 0)
19        {
20            cout << "Illegal argument to power.\n";
21            exit(1);
22        }
23        if (n > 0)
24            return ( power(x, n − 1) * x);
25        else // n == 0
26            return (1);
27    }

Sample Dialogue

3 to the power 0 is 1
3 to the power 1 is 3
3 to the power 2 is 9
3 to the power 3 is 27

Our main reason for defining the function power is to have a simple example of a recursive function, but there are situations in which the function power would be preferable to the function pow. The function pow returns values of type double, which are only approximate quantities. The function power returns values of type int, which are exact quantities. In some situations, you might need the additional accuracy provided by the function power.

The definition of the function power is based on the following formula:

xⁿ is equal to xⁿ⁻¹ * x

Translating this formula into C++ says that the value returned by power(x,n) should be the same as the value of the expression

power(x, n − 1) * x

The definition of the function power given in Display 14.3 does return this value for power(x, n), provided n > 0. The case where n is equal to 0 is the stopping case. If n is 0, then power(x,n) simply returns 1 (since x⁰ is 1).

Let’s see what happens when the function power is called with some sample values. First consider the following simple expression:

power(2, 0)

When the function is called, the value of x is set equal to 2, the value of n is set equal to 0, and the code in the body of the function definition is executed. Since the value of n is a legal value, the if-else statement is executed. Since this value of n is not greater than 0, the return statement after the else is used, so the function call returns 1. Thus, the following would set the value of y equal to 1:

int y = power(2, 0);

Now let’s look at an example that involves a recursive call. Consider the expression

power(2, 1)

When the function is called, the value of x is set equal to 2, the value of n is set equal to 1, and the code in the body of the function definition is executed. Since this value of n is greater than 0, the following return statement is used to determine the value returned:

return ( power(x, n − 1) * x );

which in this case is equivalent to

return ( power(2, 0) * 2 );

At this point the computation of power(2,1) is suspended, a copy of this suspended computation is placed on the stack, and the computer then starts a new function call to compute the value of power(2,0). As you have already seen, the value of power(2,0) is 1. After determining the value of power(2,0), the computer replaces the expression power(2,0) with its value of 1 and resumes the suspended computation. The resumed computation determines the final value for power(2,1) from the return statement above as follows:

power(2, 0) * 2 is 1 * 2, which is 2.

Thus, the final value returned for power(2,1) is 2. The following would therefore set the value of z equal to 2:

int z = power(2, 1);

Larger numbers for the second argument will produce longer chains of recursive calls. For example, consider the statement

cout << power(2, 3);

The value of power(2, 3) is calculated as follows:

power(2, 3) is power(2, 2) * 2
power(2, 2) is power(2, 1) * 2
power(2, 1) is power(2, 0) * 2
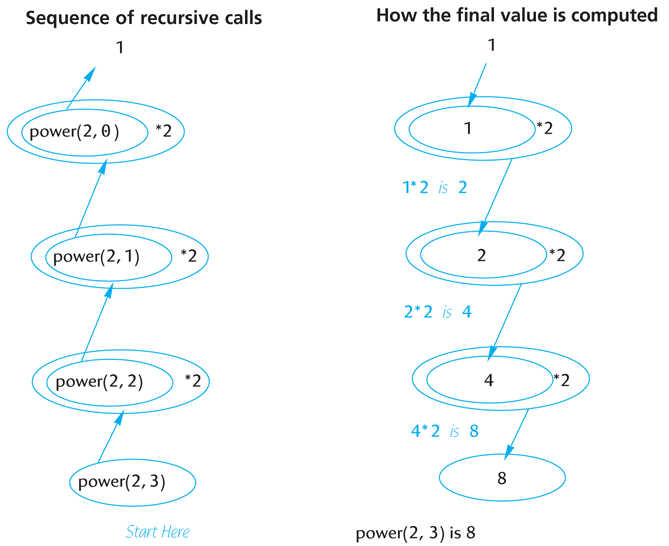
power(2, 0) is 1 (stopping case)

When the computer reaches the stopping case, power(2,0), there are three suspended computations. After calculating the value returned for the stopping case, it resumes the most recently suspended computation to determine the value of power(2,1). After that, the computer completes each of the other suspended computations, using each value computed as a value to plug into another suspended computation, until it reaches and completes the computation for the original call, power(2,3). The details of the entire computation are illustrated in Display 14.4.

A diagram for evaluating the recursive function call power (2, 3). — Display 14.4 Evaluating the Recursive Function Call `power (2, 3)`

Figure 14.4 Full Alternative Text

Self-Test Exercises

What is the output of the following program?

#include <iostream>
using namespace std;
int mystery(int n);
//Precondition n > = 1.
int main()
{
    cout << mystery(3);
    return 0;
}
int mystery(int n)
{
    if (n < = 1)
        return 1;
    else
        return ( mystery(n − 1) + n );
}

What is the output of the following program? What well-known mathematical function is rose?

#include <iostream>
using namespace std;
int rose(int n);
//Precondition: n >= 0.
int main()
{
    cout << rose(4);
    return 0;
}
int rose(int n)
{
    if (n <= 0)
        return 1;
    else
        return ( rose(n − 1) * n );
}

Redefine the function power so that it also works for negative exponents. In order to do this, you will also have to change the type of the value returned to double. The function declaration and header comment for the redefined version of power is as follows:
```
double power(int x, int n);
//Precondition: If n < 0, then x is not 0.
//Returns x to the power n.
```
(Hint: x^–n is equal to 1/(xⁿ).)