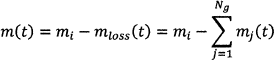
The melting rate of high-level waste (HLW) glass strongly affects the vitrification process and the efficiency of immobilization of nuclear waste. A key factor influencing the melting rate is the conversion of the dry melter feed to glass within the batch blanket or “cold cap,” a layer of melter feed floating on a pool of molten glass in an electrical glass-melting furnace. Such conversion involves numerous reactions, which typically generate gases. Using thermogravimetry coupled with gas chromatography-mass spectrometry, we performed analyses of multiple gas-evolving reactions and evolving gases (H2O, CO2, NO and O2). We further developed a simple model, via the least squares method, which correlates the overall mass loss rate to the gas evolution rates of each gas with constant fitting coefficients. The agreement with the measured mass loss rate is nearly perfect. The fitting coefficients can be used to determine the amount of mass loss equivalent to each evolving gas.
Keywords: Cold-cap reactions, Evolved gas analysis, Nuclear waste vitrification, Calibration model, glass melting.
The cost and schedule of high-level waste (HLW) treatment is highly dependent on the loading of HLW in glass and on the rate of HLW glass production. In a continuously fed glass melter, the rate of processing is jointly controlled by the rate of heat transfer from molten glass to the cold cap and by the kinetics of various chemical reactions and phase transitions within the cold cap.1’ The cold cap is a mixture of low-melting salts, glass-forming melts, undissolved refractory solids (sometimes in clusters), and various gases.4 For vitrifying nuclear waste glass,4–7 the feed, a mixture of waste with glass-forming and -modifying additives, is charged onto the cold-cap that covers 90–95% of the melt surface.
As the feed moves through the cold cap, it undergoes chemical reactions and phase transitions through which it is converted to molten glass that moves from the cold cap into the melt pool. The nuclear waste itself contains 40 to 60 elements forming water-soluble salts, amorphous gels, and crystalline minerals. The conversion to glass proceeds over a wide range of temperatures (~100–1100°C) spanning the formation of molten salts that react with feed solids, turning them into intermediate products and ultimately the glass-forming melt. Various cold-cap reactions evolve gases that escape from the cold cap through open pores and through the bottom foam layer that develops beneath the cold cap.5 Understanding the cold-cap reactions over the temperature range of the conversion process helps formulate melter feeds for higher production rate, and hence an enhanced efficiency of the vitrification facility.
Gas-evolving cold-cap reactions release chemically bonded water and produce NOx, O2, and COx from reactions of nitrates with organics and reactions of nitrates, nitrites and carbonates with solids.8–20 Evolved gas analysis (EGA) allows the identification of gases released and the determination of their amounts as a function of temperature while the sample is subjected to a controlled temperature program. Previous informative, yet semi-quantitative, EGA studies analyzed off-gas from a lab-scale furnace but were unable to determine contributions of each gas to the mass losses.21–23 Here, we illustrate the correlation between the gases detected by gas chromatography-mass spectrometry (GC-MS) and the mass loss rate from thermogravimetry to obtain a quantitative analysis of contributions of individual gases to mass losses associated with the feed-to-glass conversion.
Assuming that the mass loss of the batch is only associated with gas evolution reactions7 the mass of the feed batch at time t is
where mi is the initial mass, mloss is the mass loss, mj is the mass loss associated with they jth off-gas, and Ng is the number of gas species. Differentiating Eq. (1) with respect to time yields
For analysis with GC-MS, the flux of each gas species, represented via abundance, is proportional to the number of molecular ions (or instrumentally induced charges or produced current). Provided that instrumental artifacts are negligible, quantitative analysis can be established by assuming that the mass change rate of they jth off-gas is linearly proportional to the jth off-gas abundance or intensity, Ij. Thus,
where Fj is the jth off-gas calibration coefficient; Fj is dimensionless such that FjIj has an appropriate mass/(time)2 unit. Here Δt represents a time lag, assumed to be invariant over time or temperature, between the thermogravimetric analysis (TGA) signal and the MS detector reading, due to the off-gas transfer to the MS detector. Inserting Eq. (3) into Eq. (2), one obtains
Eq. (4) correlates the mass loss rate, dm(t)/dt, from TGA, with the Ij from MS via Ng calibration coefficients, which can be obtained using the least squares method.
Under ideal experimental conditions, similar to calibrations performed for quantitative and semi-quantitative MS analyses shown elsewhere,24 a jth calibration coefficient can be established by comparing the integrated intensity with the mass change of a solid sample that releases the jth gas in a single reaction. Accordingly,
(5) 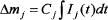
where Cj is the jth gas calibration coefficient and Δmj is the mass change of the solid sample during the gas-evolving process. The range of integration is determined by the start and end of the gas-evolving reaction that generates the gas.
The measurements were performed using simultaneous TGA-GC-MS. The TG 449 F1 Jupiter® (NETZSCH) is attached to the Agilent 7820A gas chromatograph—Agilent Technologies 5975 series mass spectrometer.25 A heated gas transfer from the thermogravimetric (TG) analyzer (TG) to the valve box and the injector at the GC serves as the coupling mechanism. The GC-MS is controlled by the Agilent ChemStation software triggered by the NETZSCH Proteus® software that controls the TGA. The instrument was calibrated according to manufacturer guidelines.26 The CG-MS efficiency was checked by a semi quantitative analysis of CaCO3.
A simulated high-alumina melter feed (A0), composition is shown in Table I, was used in this study. The feed was formulated to vitrify a high-alumina HLW to produce glass with the following composition in mass fractions: SiO2 (0.305), Al2O3 (0.240), B2O3 (0.152), Na2O (0.096), CaO (0.061), Fe2O3 (0.059), Li2O (0.036), Bi2O3 (0.011), P2O5 (0.011), F (0.007), Cr2O3 (0.005), PbO (0.004), NiO (0.004), ZrO2 (0.004), SO3 (0.002), K2O (0.001), MgO (0.001), and ZnO (0.001).7,21,27 This glass was designed for the Hanford Tank Waste Treatment and Immobilization Plant, currently under construction at the Hanford Site in Washington State, USA.28 The batch was heated and stirred at a constant rate to 60 to 80°C, and dried overnight at 105°C, as described elsewhere.27
Table I. Melter feed composition of glass A0
| Chemicals | Mass(g) |
| Al(OH)3 | 367.49 |
| H3BO3 | 269.83 |
| CaO | 60.79 |
| Fe(OH)3 | 73.82 |
| Li2CO3 | 88.30 |
| Mg(OH)2 | 1.69 |
| NaOH | 99.41 |
| SiO2 | 305.05 |
| Zn(NO3)2·4H2O | 2.67 |
| Zr(OH)4·0.65H2O | 5.49 |
| Na2SO4 | 3.55 |
| Bi(OH)3 | 12.80 |
| Na2CrO4 | 11.13 |
| KNO3 | 3.04 |
| NiCO3 | 6.36 |
| Pb(NO3)2 | 6.08 |
| Fe(H2PO2)3 | 12.42 |
| NaF | 14.78 |
| NaNO2 | 3.37 |
| Na2C2O4 | 1.26 |
| Total | 1349.32 |
The thermal decomposition of calcium carbonate has been intensively studied due to its wide industrial application and an apparent simplicity of the reaction. Calcium carbonate decomposition reaction involves a relatively large mass loss associated with CO2 evolution according to the reaction29
(6) 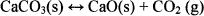
This compound is an appropriate reference for the TGA-GC-MS system because its decomposition stoichiometry is well known, the product is not hygroscopic, and the decomposition steps are distinct and well resolved.30 The TG experiment was completed by heating 6.5 mg CaCO3 at 10°C min−1 from 50°C to 1200°C in a 20-ml min−1 helium flow. The evolved gases were analyzed using GC-MS. The National Institute of Standards and Technology (NIST) mass spectral database, which contains a collection of electron ionization mass spectra for various molecular species, was used in this analysis.
After chromatographic separation, the evolved gas, CO2, was identified by its mass spectra through the interactive library search. The measured CaCO3 weight loss of 43.20% compares well with the stoichiometric weight loss of 43.96%. Because of the instrument configuration and GC column, a lag time was considered to adjust the MS curve and TG mass loss. The MS and weight derivative (DTG) plots are combined in Figure 1 and show that CaCO3 thermal decomposition takes place between 530°C and 775°C.
Figure 1. TG-MS (m/z = 44) (solid line) and DTG curves of CaCO3 decomposition at 10°C min−1 heating rate (dotted line).

The TG experiment on A0 feed was accomplished by placing 6.7 mg of feed into a 30-μl platinum crucible that is specifically used for thermal analysis. The feed sample was heated in a 20-ml min−1 He flow at 10 K min−1 from 50°C to 1200°C. The evolved gas was carried at 200°C to the GC heated valve loop by the heated transfer line. GC-MS uses He as carrier gas at a 2 ml min−1 flow rate. The GC is equipped with a GS-CarbonPLOT capillary column that offers high stability for light gases. Oven and valve box temperatures were constant at 200°C for 111 minutes. MS ionization energy was set to 20 eV, the scan range m/z (the mass-to-charge ratio) was 10–100, and the the GC-MS interface was set to 280°C. Figure 2 shows the raw TGA data. The output signals from the MS are shown in Figure 3.
Figure 2. TGA normalized weight loss and normalized weight derivative (DTG) of A0 feed heated at 10 K min−1. The GC-Mass spectrogram in Figure 3 identifies four gases: CO2, H2O, NO, and O2.

Figure 3. GC-Mass spectrogram of A0 feed heated at 10 K min−1.

Using the NIST database, the gases were identified by their decomposition masses: m/z = 44 for CO2, 18 for H2O, 30 for NO, and 32 for O2. The major gases were CO2 and H2O. The generation of O2 was appreciable only at T ≥ 900°C. The minor NO peak coincides with the major peak of CO2.
To match the DTG and GC-MS temperature scales, data were smoothed with spline interpolation and a ~1.5-min time lag was applied. The time lag of the off-gas transfer from the TGA to the MS detector corresponds to the 1.5-mL min−1 flow rate through the 30-m column with an inner diameter of 320 μm.
Calibration coefficients (Fj) (Table II) were obtained using least squares analysis by minimizing the value of the expression
Table II. Calibration coefficients for individual evolved gases
| Gas | Calibration coeficient |
| H2O | 1.15×10−6 |
| CO2 | 1.36×10−7 |
| NO | 2.98×10−7 |
| O2 | 7.20×10−8 |
(7) 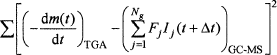
where the subscripts indicate the source of data.
To resolve the issue of overlapped CO2 and NO peaks, the least squares optimization was constrained using the NO/CO2 ratio of 0.0732 based on the content of carbon and nitrogen in the feed. The difficulty of quantifying the O2 release was bypassed by applying separate least squares analyses to T < 690°C for H2O and CO2 and T > 690°C for O2.
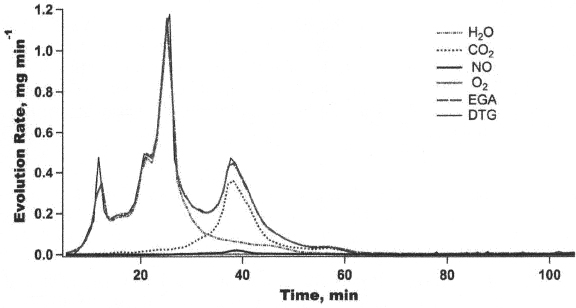
Figure 4 compares the mass change rates from DTG with GC-MS gas evolution rates obtained with the Fj values listed in Table II. The EGA curve in Figure 4 represents total gas evolution rate. The good agreement between DTG and EGA in Figure 4 demonstrates that Eq. (4) yields a reasonable simulation.
Figure 4. Gas evolution rates for gaseous species by TGA and GC-MS
Performance of the coupled system and model over time intervals is shown in Figure 5, where dm(t)/dt at the t from TGA is plotted against  from GC-MS. This comparison shows reasonable agreement.
from GC-MS. This comparison shows reasonable agreement.
Figure 5. Comparison of instantaneous mass loss rate by TGA and by GC-MS.

The TG-GC-MS analysis identifies gases evolved from melter feeds during their conversion to molten glass. A simple calibration model correlates the mass loss rate from TGA to the production rate of individual gases from EGA on a quantitative basis. This identifies where specific mass loss occurs as melter feed is heated and goes through various reactions and releases CO2, H2O, NO, and O2.
This work was supported by the Department of Energy’s Waste Treatment & Immobilization Plant Federal Project Office under the direction of Dr. Albert Kruger. The authors are grateful to Drs. Dong-Sang Kim and Ekkehard Post for insightful discussions and instructions on the TGA-GC-MS setup and tests, respectively. Pacific Northwest National Laboratory is operated by Battelle Memorial Institute for the U.S. Department of Energy under contract DE-AC05-76RL01830.
1P. Hrma, Melting of Foaming Batches: Nuclear Waste Glass, Glastech. Ber. 63K:360 (1990).
2P. Hrma, J. Matyáš, and D-S Kim, The Chemistry and Physics of Melter Cold Cap, In: 9th Biennial Int. Conf. on Nucl. and Hazardous Waste Management, Spectrum ‘02, American Nuclear Society, La Grange Park, IL (2002).
3D.F. Bickford, P. Hrma, and B.W. Bowen, II, Control of Radioactive Waste Glass Melters: II, Residence Time and Melt Rate Limitations, J. Amer. Ceram. Soc. 73,2903 (1990)
4D. Kim, M.J. Schweiger, W.C. Buchmiller, and J. Matyas, Laboratory-Scale Melter for Determination of Melting Rate of Waste Glass Feeds, (2012).
5R. Pokorný and P. Hrma, Mathematical modeling of cold cap, J. Nucl. Mater. 429, 245–256 (2012).
6P. Hrma, A.A. Kruger, and R. Pokorný, Nuclear waste vitrification efficiency: cold cap reactions, J. Non-Cryst. Solids, 358, 3559–3562 (2012).
7R. Pokorný, D.A. Pierce, and P. Hrma, Melting of glass batch: Model for multiple overlapping gas-evolving reactions, Thermochim. Acta 541, 8–14 (2012).
8F.W. Wilburn and C.V. Thomasson, The application of differential thermal analysis and thermogravimetric analysis to the study of reactions between glass-making materials. Part 1. The sodium carbonate–silica system, J. Soc. Glass Technol. 42, 158T–175T (1958).
9C.V. Thomasson and F.W. Wilburn, The application of differential thermal analysis and thermogravimetric analysis to the study of reactions between glass-making materials. Part 2. The calcium carbonate–silica system with minor batch additions, Phys. Chem. Glasses 1, 52–69 (1960).
10F.W. Wilburn and C.V. Thomason, The application of differential thermal analysis and thermogravimetric analysis to the study of reactions between glass-making materials. Part 3. The sodium carbonate–silica system, Phys. Chem. Glasses 2, 126–131 (1961).
11F.W. Wilburn and C.V. Thomason, The application of differential thermal analysis and differential thermogravimetric analysis to the study of reactions between glass-making materials. Part 4. The sodium carbonate–silica–alumina system, Phys. Chem. Glasses 4, 91–98 (1963).
12F.W. Wilburn, S.A. Metcalf, and R.S. Warburton, Differential thermal analysis, differential thermogravimetric analysis, and high temperature microscopy of reactions between major components of sheet glass batch, Glass Technol. 6, 107–114 (1965).
13E. Bader, Thermoanalytical investigation of melting and fining of Thüringen laboratory glassware, Silikattechnik 29, 84–87 (1978).
14J. Mukerji, A.K. Nandi, and K.D. Sharma, Reaction in container glass batch, Ceram. Bull. 22, 790–793 (1979).
15O. Abe, T. Utsunomiya, and Y. Hoshino, The reaction of sodium nitrate with silica, Bull. Chem. Soc. Jpn. 56, 428–433 (1983).
16T.D. Taylor and K.C. Rowan, Melting reactions of soda-lime-silicate glasses containing sodium sulfate, J. Am. Ceram. Soc. 66, C227–228 (1983).
17M. Lindig, E. Gehrmann, and G.H. Frischat, Melting behavior in the system SiO2-K2CO3-CaMg(CO3)2 and SiO2-K2CO3-PbO, Glastech. Ber. 58, 27–32 (1985).
18C.A. Sheckler and D.R. Dinger, Effect of particle size distribution on the melting of soda-lime-silica glass, J. Am. Ceram. Soc. 73, (1990) 24–30 (1990).
19K.S. Hong and R.E. Speyer, Thermal analysis of reactions in soda-lime-silicate glass batches containing melting accelerants: I. One- and two-component systems, J. Am. Ceram. Soc. 76, 598–604 (1993).
20K.S. Hong, S.W. Lee, and R.E. Speyer, Thermal analysis of reactions in soda-lime-silicate glass batches containing melting accelerants: II. Multicomponent systems, J. Am. Ceram. Soc. 76, 605–608 (1993).
21J. Chun, D.A. Pierce, R. Pokorný, and P. Hrma, Cold-cap reactions in vitrification of nuclear waste glass: experiments and modeling. Thermochim. Acta 559 (2013) 32–39.
22P.A. Smith, J.D. Vienna, and P. Hrma, The effects of melting reactions on laboratory-scale waste vitrification. J. Mater. Res. 10, 2137–2149 (1995).
23J. Matyáš, P. Hrma, and D.-S. Kim, Melt Rate Improvement for High-Level Waste Glass, PNNL-14003, Pacific Northwest National Laboratory, Richland, Washington, (2002).
24C.-A. Craig, K.E. Jarvis, and L.J. Clarke, An assessment of calibration strategies for the quantitative and semi-quantitative analysis of calcium carbonate matrices by laser ablation-inductively coupled plasma-mass spectroscopy (LA-ICP-MS). J. Anal. At. Spectrom. 15, 1001–1008 (2000).
25TGA-GC-MS Coupling. NETZSCH-Gerätebau GmbH.
26Software Manual STA 449 F1&F3. Temperature and Sensitivity Calibration. NETZSCH-Gerätebau GmbH
27M.J. Schweiger, P. Hrma, C.J. Humrickhouse, J. Marcial, B.J. Riley, and N.E. TeGrotenhuis, Cluster formation of silica particles in glass batches during melting, J. Non-Cryst. Solids 356, 1359–1367 (2010).
28P.R. Hrma, M.J. Schweiger, B.M. Arrigoni, C.J. Humrickhouse, J. Marcial, A. Moody, C. Rodriguez, R.M. Tate, and B. Tincher, Effect of Melter-Feed-Makeup on Vitrification Process, PNNL-18374, Pacific Northwest National Laboratory, Richland, Washington, (2009).
29Velyana Georgieva, Lyubomir Vlaev, and Kalinka Gyurova, “Non-Isothermal Degradation Kinetics of CaCO3 from Different Origin,” Journal of Chemistry, vol. 2013, Article ID 872981, 12 pages, 2013. doi:10.1155/2013/872981
30M. Maciejewski, C.A. Müller, R. Tschan, W.D. Emmerich, and A. Baiker, Thermochim. Acta, 295, 167 (1997).