Figure 1: Schematic of the cross-section of the simulated LHTESS along with the non-dimensional geometrical values.

This study predicts through numerical modeling the energy storage performance of a commercial phase change material (PCM) in a double-pipe, latent heat thermal energy storage (LHTES) heat exchanger. The heat exchanger consists of two horizontal concentric elliptical pipes. In the first part of the study, it is assumed that the PCM is within the elliptical annulus and the heat transfer fluid flows through the inner elliptical pipe while the outer pipe is insulated. In the second part of this study, it is assumed that the annulus is fitted with PCM-infiltrated high porosity aluminum foam. The numerical model uses volume averaging and employs boundary-fitted coordinate (BFC) method. In the case of metal foam and PCM, it is assumed that they remain in thermal equilibrium during the total period of melting (energy charging). When the energy storage rates are compared, PCM infiltrated metal foam shows much higher energy storage performance compared to the only PCM. The beneficial effect of natural convection melting of PCM is suppressed in the composite but this suppression is offset by the higher thermal conductivity of the metal skeleton. The inner tube thermal boundary condition and the porosity and pores per inch (PPI) of the foam are varied and the energy storage rates are compared for various cases.
Solar energy is an intermittent supply source of energy and is considered as an important renewable energy source globally. Recently the European parliament has passed a resolution recommending to all member countries to introduce legislation mandating the use of solar thermal systems in all new residential buildings [1]. There is a broad consensus among solar energy researchers that in future forty to fifty percent of the annual hot water needs of a household could be met from solar energy. To efficiently utilize this free renewable energy source some form of thermal energy storage devices are necessary. Phase change materials (PCMs). because of their high energy density storage capacity and near isothermal phase change characteristics, have proven to be promising candidates for latent heat thermal energy storage (LHTES) devices [2–5]. Among the various LHTES devices for low temperature residential heating and cooling applications, the shell-and-tube type heat exchanging devices are the most simple to operate and can be easily fabricated [2].
The PCMs offer the highest heat storage capacities per unit mass or volume in comparison to the sensible heat storage materials such as, water, stone, rock, wood, plastic, etc. A PCM, such as paraffin wax, offers four to five times higher heat capacity by volume or mass, than water at low operating temperature differences because of the latent heat transfer during phase transition. Among various PCMS, which have been identified for possible use in LHTES devices, the paraffin wax has proven to be one of the best alternatives [3]. For the following beneficial properties, such as, high heat of fusion, low melting point temperature, little volume changes on melting/solidification, low vapor pressure, less expensive and non-corrosive and save to use, have made the paraffin waxes as the ideal choice for solar and waste heat energy storage applications. The paraffin waxes consist of saturated hydrocarbon series from C14H30 to C40H82 and exhibit a suitable melting temperature range from 6°C to 80°C which is beneficial for domestic heating and cooling applications. The above hydrocarbon compounds with more than 15 carbon atoms per molecule are waxy solids at room temperature. In selecting a paraffin wax its melting temperature has to be matched to the operating temperature of the solar energy storage system. A paraffin wax with a low melting point (within 60°C) is of interest for solar energy storage systems. The paraffin with 25 to 35 carbon atoms per molecule has a melting points within 60°C [4–6].
A pure PCM with a high latent heat of fusion is capable of storing/releasing a large amount of energy during melting/solidification at a certain temperature. If the PCM is impure or is a technical grade, it will melt and solidify over a temperature range. Thus, during the transient phase-change process there will be solid, liquid and mushy regions (mixture of solid and liquid) in the LHTES systems. Pure paraffin waxes are about ten times costlier than their technical grade counter parts and as a result technical grade waxes are more cost effective compared to the pure waxes for LHTES applications. One of the problems of these waxes is the fact that they have very low thermal conductivities and as a result the energy transfer rate from or to the heat transfer fluid is very slow and this is particularly true during energy retrieval (solidification) phase. With regard to the low thermal conductivity problem of the paraffin PCMs, several ideas and systems have been proposed in the literature to enhance the heat transfer rate. In this regard, several studies are available in the literature concerning the improvements of the thermal conductivity of the PCMs for thermal energy storage devices [2]. Among the various ideas for heat transfer enhancement in LHTES systems, one of the ideas is to use high conductivity metallic foam with the PCM infiltrating the foam.
In this study, a double-pipe LHTES system, formed by two horizontal concentric elliptical pipes with a commercial grade PCM in the annulus, is numerically modeled. To the best of the authors’ knowledge, a similar study with impure PCM is not available in the literature.
A schematic view of a horizontal concentric elliptical annulus formed between an insulated outer elliptical tube and a heated inner elliptical tube is shown in Fig. 1. First an impure PCM in the annulus is considered. Then the aluminum foam infiltrated PCM composite is considered in the annulus. The thermo-physical properties of the PCM are listed in Table 1, while Table 2 lists the physical properties of the aluminum foam. The cross-sectional area of the inner elliptical pipe is equal to the cross-sectional area of a circular pipe of 1.7 cm diameter. The cross-sectional area of the outer elliptical pipe without the inner elliptical pipe is equal to the cross-sectional area of a circular pipe of diameter 4.42 cm. All geometrical dimensions have been normalized with respect to the equivalent diameter of the circular inner pipe of diameter 1.7 cm. The non-dimensional length of the semi-major axis of the outer and inner elliptical pipes is 1.69 and 0.69, respectively while the corresponding length of the semi-minor axis of the outer and inner elliptical pipes is 1.0 and 0.4, respectively. The cross-sectional area of the annulus between the outer and inner elliptical pipes is thus selected is equal to the cross-sectional area between the mentioned outer and inner circular pipes having a diameter ratio of 2.6. The above dimensions of the pipes are selected on the basis of the suggestions made in a recent study [7] which shows that a PCM in a smaller annular gap is more effective for LHTES applications particularly during the energy retrieval (solidification) phase because of the high thermal resistance from the low conductivity paraffin PCMs. It is assumed in the analysis that the PCM in the annulus is initially at a uniform temperature (Ti) which is either equal to or below the solidus temperature (Ts) of the PCM. When the initial temperature of the PCM is below its solidus temperature, this initial thermal condition is designated as sub-cooled condition and when the PCM is initially at the solidus temperature this condition is termed as zero sub-cooled condition. Without modeling the fluid flow and heat transfer problem for the HTF, it is assumed that HTF (hot water) is passing through the inner elliptical cylinder at a high speed under turbulent flow condition which is maintaining a constant wall temperature (Tw) greater than the liquidus temperature (TL) of the PCM, i.e., Tw > TL at time t > 0. The outer wall of the annulus is considered as adiabatic (insulted) throughout the whole melting process. Since the physical domain is symmetric about the vertical centerline, only one-half of the domain (right half shown by blue color) of the enclosure gap is chosen as the solution domain. This is done in order to obtain relatively rapid solutions as well as to decrease the computational time and the associated cost.
Figure 1: Schematic of the cross-section of the simulated LHTESS along with the non-dimensional geometrical values.

Table 1: Thermo-physical properties of PCM (Paraffin wax) and geometrical parameters
| Properties | Value |
| Thermal conductivity (liquid or solid) (k) | 0.22 W / m K |
| Density (liquid or solid) (ρ) | 790 kg/m3 |
| Specific heat (liquid or solid) (CP) | 2.15 kJ/kg K |
| Latent heat of melting (λ) | 190 kJ/kg |
| Liquidus temperature (TL) | 59.9 °C |
| Solidus temperature (TS) | 51.2 °C |
| Kinematic viscosity (μ) | 5.2 × 10−6 m2/s |
| Liquid thermal expansion coefficient (β) | 1.0E-03 1/°C |
| Equivalent inner cylinder diameter (di) | 0.017 m |
| Equivalent outer cylinder diameter (do) | 0.0442 m |
Table 2: Thermo-physical properties of aluminum foam
| Properties | Value |
| Thermal conductivity (kp) | 0.227 kW / m K |
| Density (ρp) | 2710 kg/m3 |
| Specific heat (CP) | 0.902 kJ/kg K |
| Porosity (ε) | 0.90 or 0.95 |
| Pores per inch (PPI) | 20 or 40 |
In developing the mathematical model for the LHTES system, the following assumptions were made: (a) the melt behaves as an incompressible Newtonian fluid; (b) the convective motion in the melt is transient, laminar and two-dimensional; (c) no-slip conditions are applicable for the velocity components at the boundaries; (d) thermo-physical properties of the PCM are assumed to be constant in both solid and liquid phases except for the density variations in the melt are considered insofar as they contribute to the buoyancy forces; (e) buoyancy forces are incorporated in the momentum equations based on the Boussinesq approximations; (f) the thermo-physical properties of the PCM are temperature independent within each phase and are evaluated at the liquidus temperature; (g) no viscous dissipation occurred in the calculation domain; (h) variation of liquid fraction in the mushy region is assumed to be a linear function of temperature; (i) the effects of volume change associated with the solid-liquid phase change are negligible and (j) there is no heat loss or gain from the surroundings. Because of the arbitrary nature of the annulus a non-orthogonal boundary Fitted coordinate (BFC) transformation technique was used to model the system in order to accurately model the boundary conditions. Since the companion paper [8] by the authors discusses in detail about the BFC method, hence only the final equations and the boundary conditions are listed here.
In curvilinear coordinates (ξ, η) the transformed governing equations for mass, momentum and energy takes the following general form:
(1) 
where the Jacobian J and the metric coefficients α, β, and γ and also the contravariant velocity components U and V are:
(2) 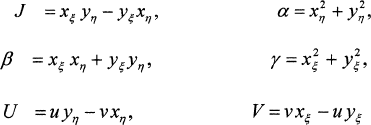
Where, Φ represents the general dependent variable and ΓΦ and SΦ (ξ, η) are associated diffusion coefficient and source term for variable Φ, respectively. The source term in the transferred equations, SΦ (ξ, η), takes on different values for different Φ’s as follows:
(3) 
(4) 
(5) 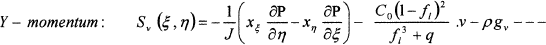
(6) 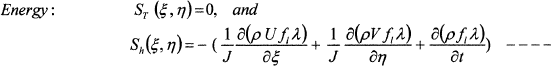
The above transformed partial differential equations have been non-dimensionalized using the following dimensionless parameters:
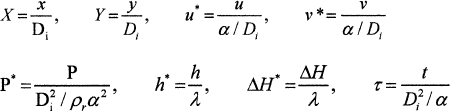
Where Di is the equivalent diameter of an inner circular cylinder, λ the latent heat of fusion. All the transformed conservation equations presented above can be expressed in a general non-dimensional transformed partial differential equation. The general form of the transformed non-dimensional governing equations becomes:
(7) 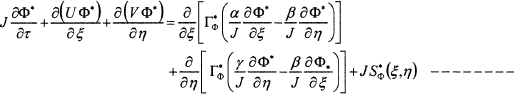
where, the values of Φ* for continuity, u and v momentum, and energy equations in new coordinate system (ξ, η) are 1, u*, v*, and h*. Γ*Φ, and S*Φ (ξ, η) are the diffusion coefficient and the source term for a general dependent variable Φ*.
For modeling of the porous foam infiltrated PCM, the above general equation was modified to represent the Brinkman-Forchheimer extended Darcy equation for mass and momentum transport in the porous media [9–13]. Also, the above equation was separately re-written for representing the energy equation in the porous media. The modeled transport equations thus appropriately considered the porosity, permeability and pores per inch (PPI) of the aluminum foam. Because of space limitations, those equations are not listed here.
Along the inner and outer pipe surfaces, no-slip boundary condition for velocities was imposed. At the symmetry plane, the normal velocity ‘u’ was taken to be zero, while the gradient of tangential velocity ‘v’ as well as the temperature were set to zero. A fixed inner wall temperature was assumed for the inner elliptical pipe, while the surface of the outer elliptical pipe enclosure was assumed to be insulated.
A control volume based finite difference technique, which was extended earlier for BFC coordinate systems [14–15], was used to solve the discretized equations and boundary conditions. The SIMPLER algorithm of Patankar [16], which stands for Semi-Implicit Method for Pressure-Linked equations revised, was employed to resolve the pressure-velocity couplings in the transformed momentum equations. The convective terms, which appeared in the discretized set of equations, were calculated using a power-law formulation. The line-by-line TDMA method [16] was used iteratively by employing suitable under-relaxation factors to obtain a converged solution. The iteration loop for the solution of the non-linear discretized equations was terminated at every time step if their maximum relative absolute residuals were less than 10−4. After carrying out grid independency tests with regard to the grid size and the time step, a grid consisting of 82 ×82 (x-, y-direction, respectively) grid points and a non-dimensional time step of 10−3 were used for all computations reported here. The code was verified by solving and by comparing the predicted results for the single phase natural convection problem in a cylindrical annulus as well as for a triangular annulus the results for which are available in the literature. Very satisfactory agreements were obtained for both cases. A detail comparison of the predicted velocity and temperature fields for the above two problems with others are given in Ref. [17].
It is to be emphasized here that the non-orthogonal BFC grid that was generated using the elliptical set of partial differential equations needed some trial and error to arrive at the optimal grid distribution. According to the present authors, it is critically important to select the boundary points on the physical domain in order to generate appropriate BFC grids. The present authors have tried a number of suggested improvements of generating BFC grids [18–21] but many failed to generate satisfactory results and many even failed to give converged results. At the end, after many months of research the authors later developed their own method of generation and implementation of the BFC grid. Figure 2 shows the generated body fitted grid points for the physical domain and the corresponding rectangular computational domain.
Fig. 2: (a) Half of the physical domain; (b) computational domain.

Two-dimensional transient numerical simulations of the melting process (energy storage) in a horizontal elliptical annulus bounded by an inner elliptical cylinder and an outer elliptical cylinder have been carried for three wall temperatures of the inner cylinder of 10, 20 and 30°C above the liquidus temperature (TL = 59.9° C) of an impure PCM and for two initial conditions of the solid PCM. The cross-section of the inner elliptical cylinder is equal to the cross-section of a circular cylinder of diameter 17.0 mm while the cross-section of the outer insulated elliptical cylinder is equal to the cross-section of a circular cylinder of diameter 44.2 mm. Only the symmetric-half of the domain has been simulated. The evolution of the predicted temperature contours and velocity vectors in the melt for the inner wall temperature of 79.9°C and zero sub-cooling of the solid PCM are illustrated in Fig. 3 through a sequence of contour plots. The left-hand frame of the plots shows the temperature contours and specifically the shape of the melt region with the mushy zone while the right-hand frame gives the corresponding velocity field. Figure 3(a) shows the condition of the impure PCM during melting at 1.85 min (τ = 0.05). It is to be noted that the red region is the melt region, yellowish green region is a portion of the mushy region with a liquid volume fraction between 1.0 and 0.5, while the light green region represents a mushy region where liquid volume fraction is between 0.5 and 0. The small blue color region in Fig. 3(a) represents the un-melted solid PCM. By tracking the temperature contour separating the red color and yellowish green regions, one can get a clear picture as how the melt region is expanding with the progression of melting. Similarly, by tracing the temperature contour of 55.5°C in Fig, 3 one can get a clear picture of the progression of the 0.5 liquid fraction region. Figure 3(a) shows that at the early stage of melting, heat storage in the PCM is mainly by conduction as is clearly evident from the uniform melt and mushy layers with concentric isotherm distribution with a weak flow field in the narrow melt layer gap. Figure 3(b) reveals that at the time instant of 3.92 min (τ = 0.1) the transition between conduction dominated melting to natural convection dominated melting is taking place. This is evident by the small pear-shaped melt region at the top of the inner cylinder. Figure 3(c) illustrates mat at 5.58 min (τ = 0.15) the solid layer above the inner cylinder is melted away and the outer cylinder is reached by the melt layer. Since the melt region cannot move further upward it is therefore extending sideways and moving along the surface of the outer cylinder. At this time, a recirculation zone (one in each side) in the melt, which is moving in the clockwise direction, has taken its foot.
Fig. 3: Left hand frame represents the temperature contours and right hand frame represents the velocity vector field. Figures 3(a-f) depict the progression of melting for six time instants for the inner wall temperature of 79.9°C and initial temperature of 51.2°C.

Figure 3(d) depicts that, at a time instant of 7.44 min (τ = 0.20), the melt region is expanding downward and the flow in the melt is intensifying due to strong natural convection effect. At this time, a strong thermal plume is developed which is being fed by the hot melt moving upward along the cylinder surface to the top region. The recirculation zone which developed in the melt earlier is much stronger at this time. The hot melt once it reached the top region, is turned back and moved downward following the much cooler liquid-mushy region. It is to be noted that, in addition to the liquid motion in the pure melt region there is also some movement of the melted liquid in the mushy region due to natural convection, albeit the velocity of the mushy liquid is much smaller compared to the liquid velocities in the melt region. Also, it is seen that the eye of the re-circulation loop in the melt has shifted downward compared to the earlier time instants. The blank regions of the left hand panels of Fig. 3 show that there is no motion of the melt when the melt fraction of the melt is below 0.5. One additional point to note here is that the melt layer thickness near the bottom of the cylinder did not change to any significant manner from earlier time instants and there is almost no heat transfer in that region with the progress of melting.
Figures 3(e) and 3(f) reveal that with the further continuation of melting the melt region progressively gets thermally stratified and the rate of melting is diminishing. Between the time instants of 9.30 min (τ = 0.25) and 11.16 min (τ = 0.30), the melting rate is not very significant and at the end of the melting period of 11.16 min, there remains an un-melted mushy layer near the bottom of the annulus. Further continuation of the melting period (not reported here) only heated the melt with very little melting of the lower mushy region. It is therefore important during the design of a LHTES unit to identify the time period after which the energy storage should be stopped since the return on the continuation of the melting period on energy storage will be minimal.
Figure 4 gives a snapshot of the condition of the PCM after a melting period of 11.16 min for the cylinder wall temperature of 69.9°C, i.e. for 10°C above the liquidus temperature of the PCM for two initial conditions of the solid PCM: one case is for zero sub-cooling and the other case is for 10°C sub-cooling. Figure 4(b) shows that because of initial sub-cooling, the melted region is smaller and the natural convection is relatively weaker compared to the case of zero sub-cooling (Fig. 4(a)). For the sub-cooling case, energy was needed to be supplied for a portion of the melting period in order to heat up the solid before latent heat energy could be stored through melting of the PCM. As a result, the melting is delayed and less energy in the form of latent heat is stored for the sub-cooling case.
Fig. 4: Left hand frame represents the temperature contours and right hand frame represents the velocity vector field for the inner wall temperature of 69.9°C at a time instant of 11.16 min; (a) initial temperature of 51.2°C; and (b) initial temperature of 41.2°C.
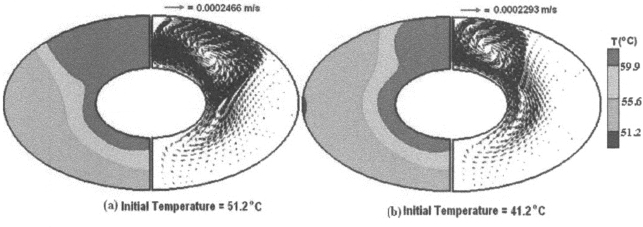
Figure 5 shows melt volume fraction (also equal to mass fraction) against time for three wall temperatures of the inner cylinder with the PCM initially at the solidus temperature (zero sub-cooling) in each case. For a constant wall temperature, the melt volume fraction increases almost linearly with time up to the melting period of 11.16 min used in the present simulation study. With the increase of the wall temperature the melt volume fraction increases with time as expected.
Fig. 5: Total melt volume fraction for three different wall temperatures at six different time instants during the melting process for an initial temperature of 51.2°C.

Figure 6 reports on the stored energy (kJ/m) for two wall temperatures of the inner cylinder, namely, for 69.9°C and 89.9°C. For each temperature two curves are plotted, one represents the latent energy stored and the other represents the total stored energy. The difference between the total and latent energies gives the sensible energy stored. With the increase of the wall temperature more energy is stored with time. One interesting point to note here is that at a higher wall temperature the difference between the total and latent energy stored is quite significant and this is particularly true even after 2 min of melting time has elapsed. For the lower wall temperature the difference between the two stored energy is not that significant. This outcome is expected since for higher wall temperatures more sensible heat in the melted PCM are stored compared to the lower wall temperatures.
Fig. 6: Total stored energy and stored latent energy in kJ/m for two different wall temperatures at six different time instants during the melting process for an initial temperature of 51.2°C.

Two-dimensional transient simulations were also carried out for PCM infiltrated high porosity aluminum foam placed in the annulus gap of the two cylinders. In numerically solving this melting problem, it was assumed that the PCM and the foam are in thermal equilibrium, a condition may which may not be applicable for the low conductivity PCM. The objective of this preliminary study to get some relevant information on this melting problem to be used in a later study without invoking the thermal equilibrium assumption. Figure 7 shows the melting patterns in terms of temperature contours and velocity vectors for the annulus for the wall temperature of 89.9°C with the PCM-foam composite initially at zero sub-cooling condition. The snapshots of the melting process for this condition are shown for six different time instants. In general, the melting rate is much faster for this case compared to the only PCM case for identical thermal boundary and initial conditions. It took about one-third the time for this case to almost complete the melting process compared to the only PCM melting case. The melting process is seen to be conduction dominated although more melting is seen occurring at the bottom of the cylinder compared to the top.
Fig. 7: Left hand frame represents the temperature contours and right hand frame represents the velocity vector field. Figures 7(a-f) depict the progression of melting for the PCM embedded in an aluminum foam (20 PPI, porosity 0.95) for six time instants for the inner wall temperature of 89.9°C for an initial temperature of 51.2°C.

Figure 8 show for a fixed PPI, how the porosity of the foam affects the melting process. For a fixed PPI of 20, two cases were simulated, in one case the porosity was assumed as 0.95 and in another case it was assumed to be 0.90. The thermal and initial conditions of the PCM were identical for both cases. An examination of this figure reveals that with the increase of porosity from 0.90 to 0.95, a slightly more energy is stored in the PCM-infiltrated foam during melting. The melt volume fraction shows an opposite trend, that is, with the increase of porosity the melt volume fraction decreases. The reason for this opposite trend is due to the fact that in a highly porous foam, more PCM is infiltrated and hence the contribution of the latent energy to the total energy is greater. But for a high porosity foam, the beneficial effect of high thermal conductivity of the foam is somewhat reduced. The PPI of the foam didn’t show any measurable effects on the melting process.
Fig. 8: Total stored energy in kJ/m and total melt volume fraction for the PCM embedded in aluminum foam for an inner wall temperature of 89.9°C at seven different time instants during the melting process for an initial temperature of 51.2°C for two porosities and for a constant pore density of 20 PPI.

With only commercial PCM inside the elliptical annulus, after a short conduction dominated period, natural convection (NC) was the dominant heat transfer mechanism during melting (charging of energy).
With the increase of the temperature of the HTF, the rate of melting due to NC increased as well as the total energy stored enhanced.
With only PCM, at the later stage of melting, thermal stratification occurred inside the annulus and a portion of the PCM was not melted within a reasonable charging period.
The initial sub-cooling of the solid PCM had a retarding effect on the melting rate as well as on the energy storage density.
For the same PCM embedded with aluminum foam, the melting rate increased by an order of magnitude compared to the bare PCM.
An increase of the porosity of the foam from 0.9 to 0.95 had a negligible impact on the melting rate and energy storage density.
The change of pore-per-inch (PPI) of the foam from 20 to 40 PPI had an insignificant impact on the melting rate.
The model and the associated code developed in not limited to a specific geometry or to a specific PCM but can be used to study the thermal storage characteristics of any shell and tube type LHTES system.
1. Source : http://www.greensunrising.com/thermal.htm).
2. Agyenium, F., Hewitt, N., Eames, P. and Smyth, M. A review of materials and phase change problem formulation for latent heat thermal energy storage systems (LETHSS). Renewable and Sustainable Energy Reviews, vol. 14, pp. 615–628, 2010.
3. Sharma, A., Tyagi, V. V., Chen, C. R. and Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renewable and Sustainable Energy Reviews, vol. 13, pp. 318–345, 2009.
4. Farid, M. M., Khudhair, A. M., Razack, S. A. K. and Al-Halliaj, S. A. A review on phase change energy storage materials and applications. Energy Conversion and Management, vol. 45, pp. 1593–1615, 2004.
5. Zalba, B., Marin, J. M., Calbeza, L. F. and Mehling, F. Review on thermal energy storage and phase change materials, heat transfer and applications. Applied Thermal Engineering, vol.23, pp. 251–283, 2003.
6. Abhat, A. Low temperature latent heat thermal energy storage system: Heat storage materials. Solar Energy, vol. 30(4), pp. 313–332, 1983.
7. Agyenim, F., Eames, P., and Smyth, M. A comparison of heat transfer enhancement in a medium temperature thermal energy storage heat exchanger using fins. Solar Energy, vol. 83, pp. 1509–1520, 2009.
8. Hasan, M., Tabassum, T. and Begum, L. Phase change thermal energy storage and recovery in a complex-shaped double pipe heat exchanger, Proceedings of the MS&T13 Conference, Oct. 27–31, 2013, Montreal, QC, Canada.
9. Li, W. Q., Qu, Z. G., He, Y. L. and Tao, W. Q. Experimental and numerical studies on melting phase change heat transfer in open-cell metallic foams filled with paraffin. Applied Thermal Engineering, vol. 37, pp. 1–9, 2012.
10. Zhou, D. and Zhao, C.Y. Experimental investigations on heat transfer in phase change materials (PCMs) embedded in porous materials. Applied Thermal Engineering, vol. 31, pp. 970–977, 2011.
11. Zhao, C. Y., Lu, W., Tian, V. Heat transfer enhancement for thermal energy storage using metal foams embedded with phase change materials (PCMs). Solar Energy, vol. 84, pp. 1402–1412, 2010.
12. Lafdi, K., Measalhy, o. and Elgafy, A. Merits of employing foam encapsulated phase change materials for pulsed power electronics cooling applications. Journal of Electronic Packaging, vol. 130, DOI 021004, 2008.
13. Nayak, K. C., Saha, S. K., Srinivasan, K. and Dutta, P. A numerical model for heat sinks with phase change materials and thermal conductivity enhancers. Int. J. Heat Mass Transfer, vol. 49, pp. 1833–1844, 2006.
14. Seyedein, S. H. and Hasan, M. Numerical investigation of coupled turbulent flow, heat transfer and macroscopic solidification in a vertical twin-roll thin-strip caster. Numerical Heat Transfer: Part A, vol. 32, no. 3, pp. 220–246 (27 pages), 1997.
15. Seyedein, S. H. and Hasan, M. Numerical simulation of turbulent flow and heat transfer in the wedge-shaped liquid metal pool of a twin-roll caster. Numerical Heat Transfer: Part A, vol. 31, no. 4, pp. 393–410, 1997.
16. Patankar, S. V. Numerical heat transfer and fluid flow. Hemisphere Publishing Co., Washington, D.C., 1984.
17. Tabassum, T. M.Eng. Dissertation, Department of Mining and Materials Engineering, McGill University, Canada, 2009.
18. Villamizar, V., and Acosta, S. Elliptic grids with nearly uniform cell area and line spacing. Electronic Transactions on Numerical Analysis, vol. 34, pp. 59–75, 2009.
19. Villamizar, V., Rojas, O. and Mabey, J. Generation of curvilinear coordinates on multiply connected regions with boundary singularities. J. of Computational Physics, vol. 223, pp. 571–588, 2007.
20. Kaul, U. K. New boundary constraints for elliptic systems used in grid generation problems. J. of Computational Physics, vol. 189, pp. 476–492, 2003.
21. Thomas, P. d. and Middlecoff, J. F. Direct control of grid point distribution in meshes generated by elliptic equations. AIAA J, vol. 18, pp. 652–656, 1980.