Chapter 3: Manipulating Data
In This Chapter
Using assignment and math operators
Understanding string manipulation
Using comparison and Boolean operators
Performing data type conversions
Every program accepts data from the outside world, manipulates that data in some way, and then calculates a useful result. Data can be
Numbers
Text
Input from a keyboard, controller, or joystick (for a video game)
To manipulate numbers, computers can perform a variety of mathematical operations, which is just a fancy way of saying a computer can add, subtract, multiply, and divide. To manipulate text (or strings, as in “text strings”), computers can perform a variety of string manipulation operations, which can chop out a letter of a word or rearrange the letters that make up a word.
Every programming language provides built-in commands (operators) for manipulating numbers and strings, but some programming languages are better at manipulating numbers (or strings) than others.
For example, FORTRAN is specifically designed to make scientific calculations easy, so FORTRAN has more operators for mathematical operations than a language such as SNOBOL, which was designed primarily for manipulating text strings. You can still manipulate strings in FORTRAN or calculate mathematical equations in SNOBOL; however, you need to write a lot more commands to do so.
Programming languages typically provide two types of data manipulation commands:
Operators are usually symbols that represent simple calculations, such as addition (+) or multiplication (*).
Functions are commands that perform more sophisticated calculations, such as calculating the square root of a number.
Unlike operators, which are usually symbols, functions are usually short commands, such as SQRT (square root).
By combining both operators and functions, you can create your own commands for manipulating data in different ways.
Storing Data with the Assignment Operator
The simplest operator that almost every programming language has is the assignment operator, which is nothing more than the equal sign (=) symbol, such as
VariableName = Value
The assignment operator simply stores or assigns a value to a variable. That value can be a fixed number, a specific string, or a mathematical equation that calculates a single value. Some examples of the assignment operator are shown in Table 3-1.
| Example | What It Does | |
|---|---|---|
| Age = 35 | Stores the number 35 into the Age variable | |
| Name = “Cat” | Stores the string “Cat” into a Name variable | |
| A = B + 64.26 | Adds the value stored in the B variable to the number 64.26 and | |
| stores the sum in the A variable | ||
| Answer = “Why” | Stores the string “Why” in the Answer variable |
Using Math to Manipulate Numbers
Because manipulating numbers (or number crunching) is such a common task for computers, every programming language provides commands for addition, subtraction, multiplication, and division. Table 3-2 lists common mathematical operations and the symbols to use.
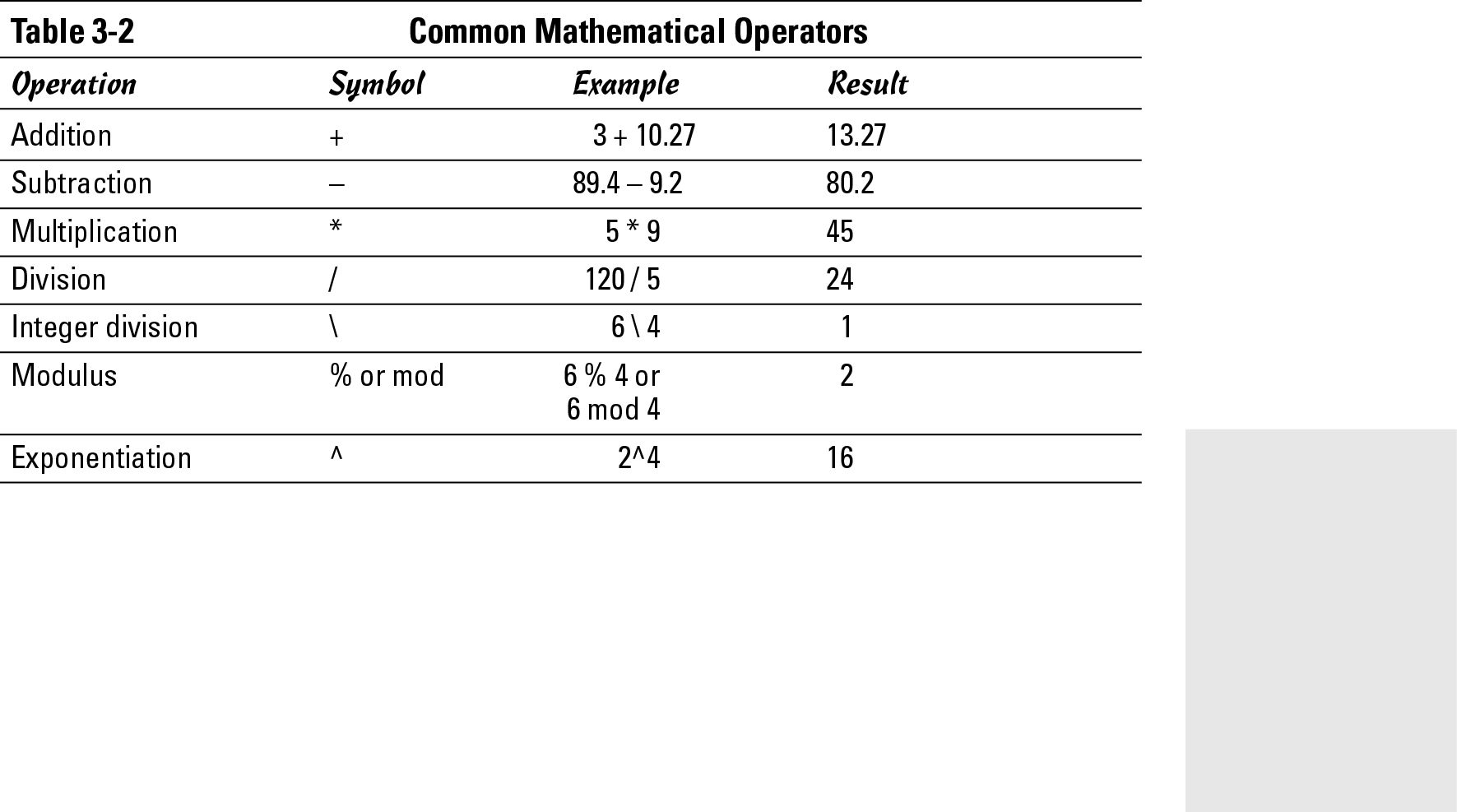
Some other examples of integer division are
23 \ 5 = 4
39 \ 7 = 5
13 \ 3 = 3
The modulus operator divides two numbers and returns the remainder. Most of the curly bracket languages, such as C++, use the percentage sign (%) as the modulus operator whereas other languages, such as BASIC, use the mod command. Some examples of modulus calculation are
23 % 5 = 3
39 % 7 = 4
13 % 3 = 1
The exponentiation operator multiplies one number by itself a fixed number of times. So the 2^4 command tells the computer to multiply 2 by itself four times or 2 * 2 * 2 * 2 = 16. Some other examples of exponentiation are
2^3 = (2 * 2 * 2) = 8
4^2 = (4 * 4) = 16
9^1 = (9 * 1) = 9
Organizing equations with operator precedence
To do multiple calculations, you can type one mathematical calculation after another, such as
X = 34 + 7
Y = X * 89
Although this works, it can get clumsy, especially if you need to write more than a handful of equations. As a simple solution, you can cram multiple equations into a single, big equation, such as
Y = 34 + 7 * 89
The problem is, how does the computer calculate this equation? Does it first add 34 + 7 and then use this result (41) to multiple with 89? Or does it first multiply 7 by 89 and then add this result (623) to 34?
Depending on the order it calculates its mathematical operators, the result is either 3649 or 657, two obviously different answers.
To calculate any equation with multiple mathematical operators, computers follow rules that define which mathematical operators get calculated first (known as operator precedence). Table 3-3 lists common operator precedence for most programming languages where the top operators have the highest precedence, and the lowest operators at the bottom of the table have the lowest precedence.
| Operator | Symbol | |
|---|---|---|
| Exponentiation | ^ | |
| Multiplication | * | |
| Division | / | |
| Integer division | \ | |
| Modulus arithmetic | % or mod | |
| Addition | + | |
| Subtraction | – |
If an equation contains operators that have equal precedence, the computer calculates the result from left to right, such as
X = 8 - 3 + 7
First, the computer calculates 8 – 3, which is 5 Then it calculates 5 + 7, which is 12.
If an equation contains operators with different precedence, the computer calculates the highest precedence operator first. Looking at this equation, you can see that the multiplication (*) operator has higher precedence than the addition (+) operator.
Y = 34 + 7 * 89
So the computer first calculates 7 * 89, which is 623 and then adds 34 to get 657.
What if you really wanted the computer to first calculate 34 + 7 and then multiply this result by 89? To do this, you have to enclose that part of the equation in parentheses, such as
Y = (34 + 7) * 89
The parentheses tell the computer to calculate that result first. So first this is how the computer calculates the preceding equation:
Y = (34 + 7) * 89
Y = 41 * 89
Y = 3649
Using built-in math functions
Using basic mathematical operators, you can create any type of complicated formulas, such as calculating a quadratic equation or a generating random numbers. However, writing equations to calculate something as common (to scientists and mathematicians, anyway) as logarithms, might seem troublesome. Not only do you have to waste time writing such an equation, but you have to spend even more time testing to make sure it works correctly as well.
So to prevent people from rewriting commonly needed equations, most programming languages include built-in math functions that are either
Part of the language itself (such as in many versions of BASIC)
Available as separate libraries (such as math libraries included with most C compilers)
The advantage of using built-in math functions is that you can use them without having to write any extra command that you may not want to do or may not know how to do. For example, how do you calculate the square root of a number?
Most likely, you won’t have any idea, but you don’t have to because you can calculate the square root of a number just by using that language’s built-in square root math function. So if you wanted to know the square root of 34 and store it in an Answer variable, you could just use the sqrt math function, such as
Answer = sqrt(34)
Table 3-4 lists some common built-in math functions found in many programming languages.
| Math Function | What It Does | Example | |
|---|---|---|---|
| abs (x) | Finds the absolute value of x | abs (–45) = 45 | |
| cos (x) | Finds the cosine of x | cos (2) = – 0.41614684 | |
| exp (x) | Returns a number raised to the power of x | exp (3) = 20.0855369 | |
| log (x) | Finds the logarithm of x | log (4) = 1.38629436 | |
| sqrt (x) | Finds the square root of x | sqrt (5) = 2.23606798 |
By using math operators and math functions, you can create complex equations, such as
x = 67 * cos (5) + sqrt (7)
Rather than plug fixed values into a math function, it’s more flexible just to plug in variables instead, such as
Angle = 5
Height = 7
X = 67 * cos (Angle) + sqrt (Height)
Manipulating Strings
Just as math operators can manipulate numbers, so can string operators manipulate strings. The simplest and most common string operator is the concatenation operator, which smashes two strings together to make a single string.
Most programming languages use either the plus sign (+) or the ampersand (&) symbol as the concatenation operator, such as
Name = “Joe “ + “Smith”
or
Name = “Joe “ & “Smith”
$Name = “Joe “ . “Smith”;
In the preceding examples, the concatenation operator takes the string “Joe “ and combines it with the second string “Smith” to create a single string that contains “Joe Smith”.
For more flexibility in manipulating strings, many programming languages include built-in string functions. These functions can help you manipulate strings in different ways, such as counting the number of characters in a string or removing characters from a string. Table 3-5 lists some common built-in string functions found in many programming languages.
| String Function | What It Does | Example |
|---|---|---|
| length (x) | Counts the number of characters in a | length (Hi there!) = 9 |
| string (x), including spaces | ||
| trim (x, y) | Removes characters from a string | trim (Mary, 1) = ary |
| index (x, y) | Returns the position of a string within | index (korat, ra) = 3 |
| another string | ||
| compare (x, y) | Compares two strings to see if they’re | compare (A, a) = False |
| identical | ||
| replace (x, y, z) | Replaces one string from within another | replace (Batter, att, ik) = |
| Biker |
Finding Strings with Regular Expressions
Before you can manipulate a string, you first must find it. Although some programming languages include string searching functions, most of them are fairly limited to finding exact matches of strings.
To remedy this problem, many programming languages (such as Perl and Tcl) use regular expressions. (A regular expression is just a series of symbols that tell the computer how to find a specific pattern in a string.)
If a programming language doesn’t offer built-in support for regular expressions, many programmers have written subprogram libraries that let you add regular expressions to your program. By using regular expressions, your programs can perform more sophisticated text searching than any built-in string functions could ever do.
Pattern matching with the single character (.) wildcard
The simplest way to search for a pattern is to look for a single character. For example, you might want to know if a certain string begins with the letter b, ends with the letter t, and contains exactly one character between. Although you could repetitively check every three-character string that begins with b and ends with t, like bat or but, it’s much easier to use a single-character wildcard instead, which is a dot or period character (.).
So if you want to find every three-letter string that begins with a b and ends with a t, you’d use this regular expression:
b.t
To search for multiple characters, use the (.) wildcard multiple times to match multiple characters. So the pattern b..t matches the strings boot and boat with the two (..) wildcards representing the two characters between the b and the t.
Of course, the b..t pattern doesn’t match bat because bat has only one character between the b and the t. Nor does it match boost because boost has more than two characters between the b and the t.
Pattern matching for specific characters
The (.) wildcard can find any character whether it’s a letter, number, or symbol. Rather than search for any character, you can also search for a list of specific characters by using the square bracket [ ] symbols.
Enclose the characters you want to find inside the square brackets. So if you want to find all strings that begin with b, end with t, and have an a, o, or u between, you could use this regular expression:
b[aou]t
The preceding example finds words, like bat or bot, but doesn’t find boat or boot because the regular expression looks only for a single character sandwiched between the b and the t characters.
As an alternative to listing the specific characters you want to find, you can also use the not (^) character to tell the computer which characters you don’t want to find, such as
b[^ao]t
This tells the computer to find any string that doesn’t have an a or an o between the b and the t, such as but. If you have the string bat, the b[^ao]t regular expression ignores it.
Pattern matching with the multiple character (*) and (+) wildcards
Sometimes you may want to find a string that has a specific character, but you don’t care how many copies of that character you may find. That’s when you can use the (*) wildcard to search for zero or more specific characters in a string.
So if you want to find a string that begins with bu and contains zero or more z characters at the end, you could use this regular expression:
buz*
This finds strings like bu, buz, buzz, and buzzzzzz. Because you want to find zero or more copies of the z character, you place the (*) wildcard after the z character.
The (*) finds zero or more characters, but what if you want to find at least one character? That’s when you use the (+) wildcard instead. To search for a character, you place the (+) wildcard after that character, such as
buz+
This finds buz and buzzzz but not bu because the (+) wildcard needs to find at least a z character.
Pattern matching with ranges
Wildcards can match zero or more characters, but sometimes you may want to know whether a particular character falls within a range or characters. To do this, you can use ranges. For example, if you want to know whether a character is any letter, you could use the pattern [a-z] as follows:
bu[a-z]
This finds strings, such as but, bug, or bus, but not bu (not a three-character string). Of course, you don’t need to search for letters from a to z. You can just as well search for the following:
bu[d-s]
This regular expression finds bud and bus but not but (because the t lies outside the range of letters from d to s).
You can also use ranges to check whether a character falls within a numeric range, such as
21[0-9]
This finds the strings 212 and 210. If you only wanted to find strings with numbers between 4 and 7, you’d use this regular expression:
21[4-7]
This finds the strings 215 but not the strings 210 or 218 because both 0 and 8 lie outside the defined range of 4–7. Table 3-6 shows examples of different regular expressions and the strings that they find.
By stringing multiple regular expression wildcards together, you can search for a variety of different string patterns, as shown in Table 3-6.
| Pattern | Matches These Strings | |
|---|---|---|
| t..k | talk | |
| tusk | ||
| f[aeiou]t | fat | |
| fit | ||
| fet | ||
| d[^ou]g | dig | |
| dmg | ||
| zo* | zo | |
| zoo | ||
| z | ||
| zo+ | zo | |
| zoo | ||
| sp[a–f] | spa | |
| spe | ||
| spf | ||
| key[0–9] | key4 | |
| p[aei].[0–9] | pey8 | |
| pit6 | ||
| pa21 |
You can always combine regular expressions to create complicated search patterns, such as the last regular expression in Table 3-6:
p[aei].[0-9]
This regular expression might look like a mess, but you can dissect it one part at a time. First, it searches for this four-character pattern:
The first character must start with p.
The second character must only be an a,
e, or i:
[aei].
The third character defines the (.) wildcard, so it can be anything from a letter, number, or symbol.
The fourth character must be a number: [0-9].
As you can see, regular expressions give you a powerful and simple way to search for various string patterns. After you find a particular string, you can manipulate it with the built-in string manipulation functions and operators in a specific programming language.
Using Comparison Operators
Unlike math and string operators that can change data, comparison operators compare two chunks of data to determine which one is bigger than the other. Table 3-7 lists common comparison operators. When comparison operators compare two items, the comparison operator returns one of two values: True or False.
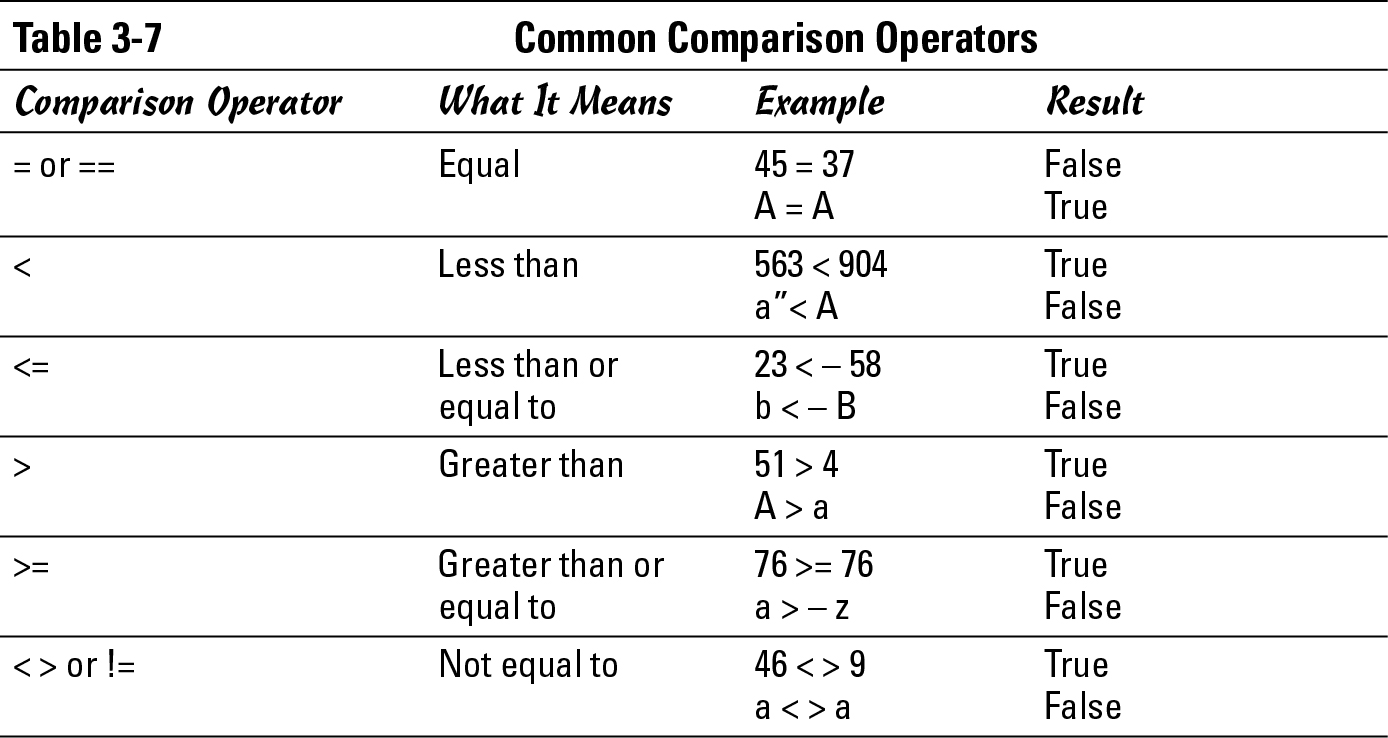
.jpg)
Comparing two numbers is straightforward, such as
5 > 2
Comparing two numbers always calculates the same result. In this case, 5 > 2 always returns a True value. What gives comparison operators more flexibility is when they compare variables, such as
Age > 2
Depending on what the value of the Age variable may be, the value of this comparison can be either True or False.
Comparing numbers may be straightforward, but comparing strings can be more confusing. Remember, computers only understand numbers, so they use numbers to represent characters, such as symbols and letters.
Computers use the number 65 to represent A, the number 66 to represent B, all the way to the number 90 to represent Z. To represent lowercase letters, computers use the number 97 to represent a, 98 to represent b, all the way up to 122 to represent z.
That’s why in Table 3-7 the comparison between A > a is False because the computer replaces each character with its equivalent code. So the comparison of characters
“A” > “a”
actually looks like this to the computer:
65 > 97
The number 65 isn’t greater than 97, so this comparison returns a False value.
Comparing a string of characters works the same way as comparing single characters. The computer examines each string, character by character, and translates them into their numeric equivalent. So if you had the comparison
“aA” > “aa”
The computer converts all the characters into their equivalent values, such as
97 65 > 97 97
The computer examines the first character of each string. If they’re equal, it continues with the second character, a third, and so on.
In the preceding example, the computer sees that the numbers 97 (which represent the character a) are equal, so it checks the second character. The number 65 (A) isn’t greater than the number 97 (a), so this comparison returns a False value.
What happens if you compare unequal strings, such as
“aA” > “a”
The computer compares each character as numbers as follows:
97 65 > 97
The first numbers of each string (97) are equal, so the computer checks the second number. Because the second string (a) doesn’t have a second character, its value is 0. Because 65 > 0, the preceding comparison returns a True value.
Now look at this comparison:
“Aa” > “a”
The computer translates these characters into their equivalent numbers, as follows:
65 97 > 97
Comparing the first numbers (characters), the computer sees that 65 > 97, so this comparison returns a False value. Notice that as soon as the computer can decide whether one character is greater than another, it doesn’t bother checking the second character in the first string.
Using Boolean Operators
Comparison operators always return a True or False value, which are Boolean values. Just as you can manipulate numbers (addition, subtraction, and so on) and strings (trimming or searching for characters), so can you also manipulate Boolean values.
When you manipulate a Boolean value, you get another Boolean value. Because there are only two Boolean values (True or False), every Boolean operator returns a value of either True or False.
Most programming languages offer four Boolean operators:
Not
And
Or
Xor
Using the Not operator
The Not operator takes a Boolean value and converts it to its opposite. So if you have a True value, the Not operator converts it to False and vice versa. At the simplest example, you can use the Not operator like this:
Not(True) = False
Like using fixed values in comparison operators (5 > 2), using fixed values with Boolean operators is rather pointless. Instead, you can use variables and comparison operators with Boolean operators, such as
Not(Age > 2)
If the value of the Age variable is 3, this Boolean operation evaluates to
Not(Age > 2)
Not(3 > 2)
Not(True)
False
Using the And operator
The And operator takes two Boolean values and converts them into a single Boolean value. If both Boolean values are True, the And operator returns a True value. Otherwise, the And operator always returns a False value, as shown in Table 3-8, or the Truth table.
| First Value | Second Value | Result |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
So if the value of the Age variable is 3, this is how the following And operator evaluates an answer:
(Age > 2) AND (Age >= 18)
(3 > 2) AND (3 >= 18)
True AND False
False
If the value of the Age variable is 25, this is how the And operator evaluates an answer:
(Age > 2) AND (Age >= 18)
(25 > 2) AND (25 >= 18)
True AND True
True
Using the Or operator
Like the And operator, the Or operator takes two Boolean values and converts them into a single Boolean value. If both Boolean values are False, the Or operator returns a False value. Otherwise, the Or operator always returns a True value, as shown in Table 3-9.
| First Value | Second Value | Result | |
|---|---|---|---|
| True | True | True | |
| True | False | True | |
| False | True | True | |
| False | False | False |
So if the value of the Age variable is 3, this is how the following Or operator evaluates an answer:
(Age > 2) OR (Age >= 18)
(3 > 2) OR (3 >= 18)
True OR False
True
If the value of the Age variable is 1, this is how the Or operator evaluates an answer:
(Age > 2) OR (Age >= 18)
(1 > 2) OR (1 >= 18)
False OR False
False
Using the Xor operator
The Xor operator is an exclusive Or. The Xor operator takes two Boolean values and converts them into a single Boolean value:
If both Boolean values are True or both Boolean values are False, the Xor operator returns a False value.
If one value is True and the other is False, the Xor operator returns a True value, as shown in Table 3-10.
| First Value | Second Value | Result |
|---|---|---|
| True | True | False |
| True | False | True |
| False | True | True |
| False | False | False |
So if the value of the Age variable is 3, this is how the following Xor operator evaluates an answer:
(Age > 2) XOR (Age >= 18)
(3 > 2) XOR (3 >= 18)
True XOR False
True
If the value of the Age variable is 1, this is how the Xor operator evaluates an answer:
(Age > 2) XOR (Age >= 18)
(1 > 2) XOR (1 >= 18)
False XOR False
False
Boolean operators are used most often to make decisions in a program, such as a video game asking, “Do you want to play again?” When you choose either Yes or No, the program uses a comparison operator, such as
Answer = “Yes”
The result depends on your answer:
If your answer is Yes, the preceding comparison operation returns a True value.
If this comparison operation is True, the video game plays again.
If your answer is No, the preceding comparison operation returns a False value.
If this comparison operation is False, the video game doesn’t play again.
Converting Data Types
Programming languages are often divided into two categories, depending on their variables:
A type-safe language forces you to declare your variables, and their data types, before you can use them.
A typeless language lets you store any type of data in a variable.
One moment a variable can hold a string, another moment it can hold an integer, and then another moment it might hold a decimal number.
Both type-safe and typeless languages have their pros and cons, but one problem with type-safe languages is that they prevent you from mixing data types. For example, suppose you need to store someone’s age in a variable. You might declare your Age variable as a Byte data type, like this in Visual Basic:
Dim Age as Byte
As a Byte data type, the Age variable can hold only numbers from 0–255, which is exactly what you want. However, what if you declare an AverageAge variable as a Single (decimal) data, and a People variable as an Integer data type, such as
Dim People as Integer
Dim AverageAge as Single
At this point, you have three different data types: Byte, Integer, and Single. Now what would happen if you try mixing these data types in a command, such as
AverageAge = Age / People
The AverageAge variable is a Single data type, the Age variable is a Byte data type, and the People data type is an Integer data type. Type-safe languages, such as C or Pascal, scream and refuse to compile and run this program simply because you’re mixing data types together.
So to get around this problem, you must use special data conversion functions that are built-in to the programming language. Data conversion functions simply convert one data type into another so that all variables use the same data type.
In the preceding example, the AverageAge variable is a Single data type, so you must convert every variable to a Single data type before you can store its contents into the AverageAge variable, such as
Dim People as Integer
Dim AverageAge as Single
Dim Age as Byte
AverageAge = CSng(Age) / CSng(People)
The CSng function converts the Age variable from a Byte to a Single data type. Then the second CSng function converts the People variable from an Integer to a Single data type. Only after all values have been converted to a Single data type can you store the value into the AverageAge variable, which can hold only a Single data type.
No matter what type of data you have, every programming language allows multiple ways to manipulate that data. The way you combine operators and functions determines what your program actually does.