• Writing mathematics
• Understanding what the various mathematical symbols mean, and how to use them
• Using BEDMAS to help with calculations
Let’s begin with one of the commonest questions in any mathematics class: “Can’t I just use a calculator?” The answer is … of course you can! This book is not selling a puritanical brand of mathematics, where everything must be done laboriously by hand, and all help is turned down. You are welcome to use a calculator for arithmetic, just as you can use a word-processor for writing text. But handwriting is an essential skill, even in today’s hi-tech world. You can use a dictionary or a spell-checker too. All the same, isn’t it a good idea to have a reasonable grasp of basic spelling?
There may be times when you don’t have a calculator or a computer to hand. You don’t want to be completely lost without it! Nor do you want to have to consult it every time a few numbers need to be added together. After all, you don’t get out your dictionary every time you want to write a simple phrase.
So, no, I don’t want you to throw away your calculator. But I would like to change the way you think about it. See it as a labor saving device, something to speed up calculations, a provider of handy shortcuts.
The way I don’t want you to see it is as a mysterious black box which performs near-magical feats that you alone could never hope to do. Some of the quizzes will show this icon 
, which asks you to have a go without a calculator. This is just for practice, rather than being a point of principle!
Mathematics has its own physical toolbox, full of calculators, compasses and protractors. We shall meet these in later chapters. Mathematics also comes with an impressive lexicon of terms, from “radii” to “logarithms,” which we shall also get to know and love in the pages ahead.
Perhaps the first barrier to mathematics, though, comes before these: it is the library of signs and symbols that are used. Most obviously, there are the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. It is interesting that once we get to the number ten there is not a new symbol. Instead, the symbols for 0 and 1 are recycled and combined to produce the name “10.” Instead of having one symbol alone, we now have two symbols arranged in two columns. Which column the symbol is in carries just as much information as the symbol itself: the “1” in “13” does not only mean “one,” it means “one ten.” This method of representing numbers in columns is at the heart of the decimal system: the modern way of representing numbers. It is so familiar that we might not realize what an ingenious and efficient system it is. Any number whatsoever can be written using only the ten symbols 0–9. It is easy to read too: you don’t have to stop and wonder how much “41” is.
This way of writing numbers has major consequences for the things that we do with them. The best methods for addition, subtraction, multiplication and division are based around understanding how the columns affect each other. We will explore these in depth in the coming chapters.
There are many other symbols in mathematics besides numbers themselves. To start with, there are the four representing basic arithmetical procedures: +, −, ×, ÷. In fact there are other symbols which mean the same things. In many situations, scientists prefer a dot, or even nothing at all, to indicate multiplication. So, in algebra, both ab and a · b, mean the same as a × b, as we shall see later. Similarly, division is just as commonly expressed by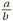 
as by a ÷ b.
This use of letters is perhaps the greatest barrier to mathematics. How can you multiply and divide letters? (And why would you want to?) These are fair questions, which we shall save until later.
Here is another common question:
“What is the point of writing out mathematics in a longwinded fashion? Surely all that matters is the final answer?”
The answer is … no! Of course, the right answer is important. I might even agree that it is usually the most important thing. But it is certainly not the only important thing. Why not? Because you will have a much better chance of reliably arriving at the right answer if you are in command of the reasoning that leads you there. And the best way of ensuring that is to write out the intermediate steps, as clearly and accurately as possible.
Writing out mathematics has two purposes. Firstly it is to guide and illuminate your own thought-processes. You can only write things out clearly if you are thinking about them clearly, and it is this clarity of thought that is the ultimate aim. The second purpose is the same as for almost any other form of writing: it is a form of communication with another human being. I suggest that you work under the assumption that someone will be along shortly to read your mathematics (whether or not this is actually true). Will they be able to tell what you are doing? Or is it a jumble of symbols, comprehensible only to you?
Mathematics is an extension of the English language (or any other language, but we’ll stick to English!), with some new symbols and words. But all the usual laws of English remain valid. In particular, when you write out mathematics, the aim should be prose that another person can read and understand. So try not to end up with symbols scattered randomly around the page. That’s fine for rough working, while you are trying to figure out what it is you want to write down. But after you’ve figured it out, try to write everything clearly, in a way that communicates what you have understood to the reader, and helps them understand it too.
The most important symbol in mathematics is “=.” Why? Because the number-one goal of mathematics is to discover the value of unknown quantities, or to establish that two superficially different objects are actually one and the same. So an equation is really a sentence, an assertion. An example is “146 + 255 = 401,” which states that the value on the left-hand side of the “=” sign is the same as the value on the right.
It is amazing how often the “=” sign gets misused! If asked to calculate 13 + 12 + 8, many people will write “13 + 12 = 25 + 8 = 33.” This may come from the use of calculators where the 
button can be interpreted to mean “work out the answer.” It may be clear what the line of thought is, but taken at face value it is nonsense: 13 + 12 is not equal to 25 + 8! A correct way to write this would be “13 + 12 + 8 = 25 + 8 = 33.” Now, every pair of quantities that are asserted to be equal really are equal − a great improvement!
The “=” sign has some lesser-known cousins, which make less powerful assertions: “<” and “>.” For example, the statement “A < B” says that the quantity A is less than B. An example might be 3 + 9 < 13. Flipping this around gives “B > A,” which says that B is greater than A, for example, 13 > 3 + 9. The statements “A < B” and “B > A” look different, but have exactly the same meanings (in the same way that “A = B” and “B = A” mean essentially the same thing).
Other symbols in the same family are “≥” and “≤,” which stand for “is greater than or equal to” and “is less than or equal to” (otherwise known as “is at least” and “is at most”).
In coming chapters, we will look at techniques for addition, subtraction, multiplication, division, and much else besides, which will allow us to judge whether or not these types of assertion are true.
Now we will have a look at one of the hidden laws of mathematical grammar.
HAVE A GO AT QUIZ 1.
One thing you may see in this book, which you may not be used to, is lots of brackets in among the numbers. Why is that? Rather than answering that question directly, I’ll pose another. What is 3 × 2 + 1? At first sight, this seems easy enough.
The trouble is that there are two ways to work it out:
a) 3 × 2 + 1 = 6 + 1 = 7
b) 3 × 2 + 1 = 3 × 3 = 9
Only one of these can be right, but which is it?
To avoid this sort of confusion, it is a good idea to use brackets to mark out which calculations should be taken together. So the two above would be written like this:
a) (3 × 2) + 1
b) 3 × (2 + 1)
Now both are unambiguous, and whichever one was intended can be written without any danger of misunderstanding. In each case, the first step is to work out the calculation inside the brackets.
NOW HAVE A GO AT QUIZ 2.
The same thing applies with more advanced topics, such as negative numbers and powers. In the coming chapters we shall see expressions such as −42. But does this mean −(42), that is to say −16, or does it mean (−4)2, which as we shall see in the theory of negative numbers, is actually + 16?
You might protest that I haven’t answered the question at the start of the last section. Without writing in any brackets, what is 3 × 2 + 1?
There is a convention which has been adopted to resolve ambiguous situations like this. We can think of it as one of the grammatical laws of mathematics. It is called BEDMAS (or sometimes BIDMAS or BODMAS). It tells us the order in which the operations should be carried out:
Brackets Exponents Division Multiplication Addition Subtraction
If you prefer, “Exponents” can be replaced by “Indices,” giving BIDMAS (or with “Orders,” giving BODMAS). All of these options are words for powers, which we shall meet in a later chapter. (Unfortunately BPDMAS isn’t quite as catchy.)
TIME FOR BEDMAS? HAVE A GO AT QUIZ 3AND 4
The point of this is that the order in which we calculate things follows the letters in “BEDMAS.” In the case of 3 × 2 + 1, the two operations are multiplication and addition. Since M comes before A in BEDMAS, multiplication is done first, and we get 3 × 2 + 1 = 6 + 1 = 7 as the correct answer.
When we come to −42, the two operations are subtraction (negativity, to be pernickety) and exponentiation. Since E comes before S, the correct interpretation is −(42) = −16.
Calculators use BEDMAS automatically: if you type in 
you will get the answer 7 not 9.
Sum up The way we think about life comes across in the way We talk and write about it. The same is true of mathematics. If you want your thought-processes to be clear and accurate, then start by focusing on the language you use!
1 Translate these sentences into mathematical symbols, and decide whether the statement is true or false.
a When you add eleven to ten you get twenty-one.
b Multiplying two by itself gives the same as adding two to itself.
c When you subtract four from five you get the same as when you divide two by itself.
d Five divided by two is at least three.
e Five multiplied by four is less than three multiplied by seven.
2 Put brackets in these expressions in two different Ways, and then, work, out the two answers. (For example from 3 × 2 + 1, we get (3 × 2) + 1 = 7 and
3 × (2 + 1) = 9.)
a 1 + 2 + 3
b 4 + 6 ÷ 2
c 2 × 3 × 4
d 20 − 6 × 3
e 2 × 3 + 4 × 5
3 In each of the expressions in quiz 2, decide which is the correct interpretation according to BEDMAS. (If it doesn’t matter, explain why.)
4 As Well as BEDMAS, there is a convention that operations are read from left to right. So 8 ÷ 4 ÷ 2 means (8 ÷ 4) ÷ 2 not 8 ÷ (4 ÷ 2). For which of addition, subtraction, multiplication, and division is this rule necessary?