
• Remembering your times tables
• Managing long multiplication
• Learning some tricks of the trade

What is multiplication? At the most basic level, it is nothing more than repeated addition. If you have five plates, each holding four biscuits, then the total number of biscuits is worked out by adding the numbers on each plate. So 5 × 4 is shorthand for five 4s being added together: 4 + 4 + 4 + 4 + 4.
This gives us our first way to calculate the answer: as long as we can add 4 to a number, we can work out 5 × 4 by repeatedly adding 4: 4, 8, 12, 16, 20. The fifth number (20) corresponds to the final plate added to the biscuit collection, and so this is the answer.
We will see some slicker techniques shortly, but the perspective of repeated addition is always worth holding in the back of your mind. It also explains another word which is commonly used to describe multiplication: “times.” The number 5 × 4 is the final result after 4 has been added 5 times.

Multiplication is usually denoted by the times symbol, ×. If you are working on a computer, though, often an asterisk * will play that role (this was originally to prevent the times sign getting muddled up with the letter X). When we get to more advanced algebra later, we will meet other ways of writing multiplication, such as 4y or 4 · y.
As with addition (but not subtraction or division), the order of the numbers does not matter. So 5 × 4 = 4 × 5, but the reason for this may not be completely obvious. To see why this is true, we can arrange the biscuits in a rectangular array as shown.

We can view this either as five columns, each containing four biscuits, giving a total of 5 × 4, or alternatively as four rows, each containing five biscuits, meaning that the total is 4 × 5. Of course this argument extends to any two numbers, meaning that for any two numbers, call them a and b, a × b = b × a.
The trouble with the “repeated addition” approach is that it is not practical for large numbers. To calculate 33 × 24 we would have to add 24s together 33 times. Most people have better ways of spending their time!
As with addition and subtraction, the key to more complex multiplication is to get to grips with the smallest numbers: 1 to 9. What this boils down to is times tables. For anyone hoping for an escape route, I am sorry to say that there is none! But there are some ways by which the pain can be reduced.
So here are some tips for mastering times tables:
• Firstly, remember the rule we saw above, that a × b = b × a. Once you know 6 × 7 you also know 7 × 6!
• The two times table is just doubling, or adding the number to itself. So 2 × 6 = 12 because 6 + 6 = 12.
• The four times table means doubling twice. So 4 × 6 = 24, because 6 + 6 = 12 and 12 + 12 = 24.
• The five times table has a simple rule: to multiply any number (such as 7) by 5, first multiply it by 10 (to get 70) and then halve the result (35).
• The nine times table also has a nice rule. Let’s look at it: 2 × 9 = 18, 3 × 9 = 27, 4 × 9 = 36, etc. There are two things to notice here. Firstly, all the answers have the property that their two digits add up to 9: 1 + 8 = 9, 2 + 7 = 9, and so on. What is more, the first digit of the answer is always 1 less than the number being multiplied by 9. So 2 × 9 = 18 begins with a 1, 3 × 9 = 27 begins with a 2, 4 × 9 = 36 begins with a 3, and so on. Putting these together gives us our rule: To multiply a single-digit number (such as 7) by 9, first reduce the number by 1 (to get 6). That is the first digit of the answer. The second digit is the difference between 9 and the digit we have just worked out (in this case, 9 − 6 = 3). Putting these together, the answer is 63.
The rules so far together cover a lot, but not everything. The first things to be missed out are these four from the three times table:
3 × 3 = 9 3 × 6 = 18 3 × 7 = 21 3 × 8 = 24
It is also worth memorizing the square numbers separately, that is, numbers multiplied by themselves (see Powers). Some of these are covered by the rules so far. The remaining ones are:
6 × 6 = 36 7 × 7 = 49 8 × 8 = 64
Finally we get to the trickiest ones! These are the three multiplications that people get wrong more than any others. It is definitely worth taking some time to remember them:
6 × 7 = 42 6 × 8 = 48 7 × 8 = 56
NOW HAVE A GO AT QUIZ 1
Even the most hard-working student can only learn times tables up to a certain limit. These days, the maximum is usually ten, which seems a sensible place to draw the line, and is the approach I’ve adopted here. When I was at school, we learned them up to 12. The more ambitious might want to push on, memorizing times tables up to 20.
Wherever you draw the line, to tackle multiplication beyond this maximum, we need a new technique. It is time to put times tables to work!
Suppose we are asked to calculate 23 × 3. Unless we have learned our three times table up to 23 (or our 23 times table up to 3), we need a new approach. One option is to break multiplication down into repeated addition: 23 + 23 + 23. But in the long run, a better method is to set up the calculation in vertical columns:
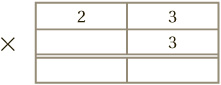
To complete this, we multiply each digit of the upper number by 3, and write it in the same column below the line. As long as we know our two and three times tables, this is straightforward:
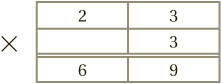
To calculate 41 × 4, we proceed exactly as before:
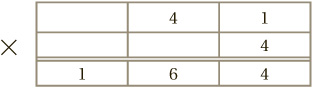
TIME FOR QUIZ 2!
This time, the tens column produces a result of 16, and we have finished.
Just as for addition, the moment that multiplication seems to become more complex is when the columns start interfering with each other, and the dreaded “carrying” becomes involved again.
Well, as I hope became clear in the addition chapter, carrying is not as confusing as you might think. In fact we have already seen some carrying in this chapter. Above, when we calculate 41 × 4, the tens column ended up with 16 in it. Of course this is too many, so it was reduced to 6, and the 1 was carried to the hundreds column, though we may not have noticed it happening.
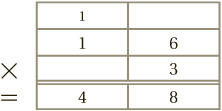
To take another example, let us say we want to calculate 16 × 3. If we just follow the rules above of multiplying each column separately, it comes out as follows:
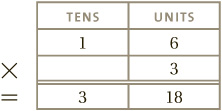
This leaves us with the correct answer, but expressed in an unusual way: thirty-eighteen. So what is that? Thinking about it, the answer must be 48.
What happens here is that the extra 1 ten from the units column gets added to the 3 in the tens column.
As with addition, it is usual to write the carried digits at the top as we go along. The crucial point to remember is:
Carried digits get added (not multiplied), to the next column, after that column’s multiplication has been completed.
So, when written out, the above calculation would look like this:
The 4 comes from the fact that three times 1, plus the carried 1, is 4.
Here is another example:
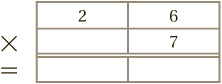
We begin with the units column, where 6 × 7 = 42. So we write down the 2 and carry the 4 to the next column:

Next, we tackle the tens column, where 7 × 2 = 14, and then we add on the carried 4 to get 18:
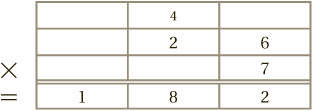
(Technically, the final step involved writing down 8, and carrying 1 to the hundreds column, where there is nothing else.)
Which is the easiest times table? Apart from the completely trivial one times table, the answer is the ten times table. Multiplying by 10 is simple: you just have to copy the original number down, and then stick a zero at the end. So 10 × 72 = 720.
To say the same thing in a different way: when writing the number in columns of units, tens and hundreds, multiplying by 10 amounts to the digits of the number each taking a step to the left. So the units move to the tens column, the tens move to the hundreds column, and so on:
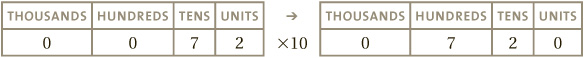
As always, any apparently “empty” columns actually have a 0 in them, which is where the extra zero on the end comes from. This perspective, of the digits stepping left when multiplied by 10, is the best one for multiplication.
Another way to think of the same thing, is that in multiplying 72 by 10, we begin at the units column, with 2 × 10, which would give 20, but this means 0 in the units column, with 2 being carried to the tens column. In the same way, the 7 is carried from the tens to the hundreds column. This leftwards step, then, is nothing more than each digit being carried, without change, straight to the next column to their left.
With this in mind, multiplying by 20 or 70 becomes as easy as multiplying by 2 or 7. So 9 × 20 = 180, just because 9 × 2 = 18, and then the digits take a step to the left.
IT’S TIME FOR A GO AT QUIZ 3.
This technique combines well with the previous section. When faced with a calculation such as 53 × 30, we proceed exactly as for 53 × 3, but placing a 0 in the units column, and shifting each subsequent digit one column to the left:

We nearly have the techniques in place to multiply any two numbers. All that remains is to bring it all together. The critical insight at this stage is this: multiplying some number, say 74, by 52 is the same as multiplying it by 50, and separately multiplying it by 2, and then adding together the two answers. Remember this chapter’s golden rule!
Why should this be? Suppose I am the door-keeper at a concert. The entry charge is 52 pence. To make life easy, let’s suppose that everyone pays with a 50p coin and two 1p coins. If 74 people come in, then how much money have I received? The answer, of course, is the number of customers times the price: 74 × 52 pence. But I decide to work it out differently, and calculate the total I have received in 50p coins (74 × 50), and then add that to the amount I have received in 1p coins (74 × 2). Of course the answer should be the same, that is to say: 74 × 52 = 74 × 50 + 74 × 2.
We can push this line of thought further. By exactly the same reasoning, it is also true that 74 × 50 = 70 × 50 + 4 × 50 and similarly that 74 × 2 = 70 × 2 + 4 × 2. (Just alter the numbers in the concert example!) This provides us with a way to calculate the answer to 74 × 52, known as the grid method. We work inside a grid, with one of the two numbers to be multiplied going along the top, and the other along the left-hand side. Then each of the two is split up into their tens and units components:
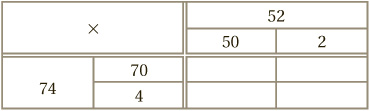
Inside the grid, we then perform the resulting four multiplications:
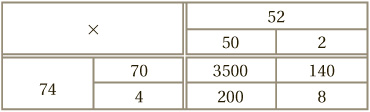
The final stage is to add these four new numbers together, to arrive at the final answer: 3500 + 200 + 140 + 8 = 3848.
The grid method easily extends to three-digit numbers. But it becomes quite time-consuming, as we have to perform nine separate calculations. For instance, to calculate 136 × 495 we split it up as follows:
IF YOU THINK YOU CAN MANAGE THAT, TRY QUIZ 4.
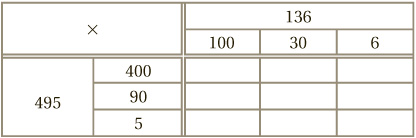
All that remains is to fill in the gaps, and add them up.
I think the grid method for multiplication is an excellent way to get used to multiplying larger numbers. So, if you are unsure of your foothold on this sort of terrain, my suggestion is to persevere with the grid method until you get comfortable with it.
Once you are used to the grid method, however, there is another step you can take: the column method. This has the advantage of taking up less space on the page, and less time, as it needs a much smaller number of individual calculations.
Essentially the idea is to split up one of the two numbers into hundreds, tens, and units, as occurs in the grid method, but not the other. This amounts to calculating each row of the grid in one go. (With three-digit numbers, this reduces the list of numbers to be added from nine to three.)
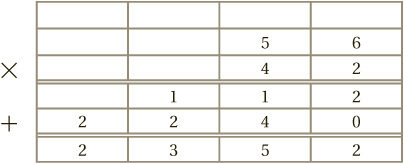
As its name suggests, we are back to working in columns instead of grids. It works like this: to calculate 56 × 42 write the two numbers in columns.

Next, ignore the “4,” and simply multiply 56 by 2, by the usual method of “carrying”:
Then we swap: ignore the 2 in the 42 (and the new 112), and this time multiply 56 by 40. Remember that this entails multiplying by 4, and shifting the answer one step to the left:
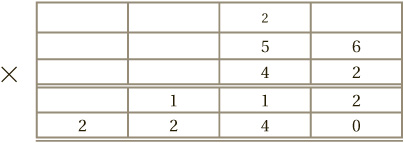
The final stage is to add the two bottom lines together:
IT’S TIME TO TAKE ON THE FINAL QUIZ, NUMBER 5.
Sum up Build up multiplication step by step, starting with repeated addition, until long multiplication is easy!
 1 A times table test!
1 A times table test!
a 2 × 8
b 5 × 6
c 6 × 9
d 7 × 7
e 7 × 8
 2 In columns
2 In columns
a 34 × 2
b 22 × 4
c 31 × 3
d 64 × 2
e 41 × 5
 3 March to the left
3 March to the left
a 44 × 20
b 23 × 30
c 12 × 40
d 63 × 30
e 71 × 50
 4 Multiplication in a grid
4 Multiplication in a grid
a 34 × 21
b 45 × 34
c 62 × 45
d 71 × 123
e 254 × 216
 5 Long multiplication in columns
5 Long multiplication in columns
a 76 × 12
b 61 × 34
c 57 × 29
d 152 × 73
e 313 × 84