• Interpreting decimals such as 0.0789
• Understanding what happens to the decimal point during arithmetic
• Mastering rounding
Not everything can be measured as whole numbers. It may not take a whole number of minutes to walk to the shop, a recipe may not require exactly a whole number of liters of milk. When we need to divide things up more finely than the whole numbers allow, there are two main approaches: fractions and decimals.
Neither method is better than the other; both are in use all the time. So it is important to be able to translate between the two. As a very rough rule of thumb, when the fraction is a simple one, it is best to use that: so we might speak of “half an apple,” or “three quarters of a mile.” But it is not practical to talk about “thirteen twenty-sevenths of a liter.” So when real precision is needed, I recommend decimals.
With that all said, what exactly is a “decimal”? The idea comes from the column representations of whole numbers that we have met in earlier chapters. There, we had columns for units, tens, hundreds, thousands, and so on, like this:
To incorporate things smaller than units, this system gets extended. We introduce new columns for tenths of a unit, and similarly for hundredths, thousandths, and so on, like this:
There is a mental adjustment we need to make when working with decimals. When we are just writing whole numbers, we know that the units column is the always the one furthest to the right. So “28” must mean this:
But when we move into the realm of decimals, we have new columns to the right of the units. Now the digits alone do not make it clear where the units are, or which column is on the right. So “287” might mean:
or:
or many other variations on the theme. This is a disaster!
The problem is solved with a new ingredient: the “decimal point.” This is a dot which sits to the right of the units column. It is this point which anchors the columns, allowing us to tell which is which. So “28.7” means:
while “2.87” means:
One consequence is that whole numbers directly translate into decimals with the addition of 0s in the columns for tenths, hundreds, thousandths, etc. So “34.0,” “34.00,” “34.000,” and so on, all mean exactly the same as “34.”
(Some countries and languages use a “decimal comma” instead of a decimal point, but it serves exactly the same purpose.)
The great thing about decimals is that the old column-based methods of arithmetic transfer straight over to this new context. So to calculate 3.3 + 5.8, we set it up in columns exactly as we did for addition of whole numbers, just making sure to line up the decimal points of all the numbers involved:
We proceed as before, making sure to start with the rightmost column, and then carrying 1 to the next column as needed:
IF YOU’RE HAPPY ADDING WHOLE NUMBERS, TRY QUIZ 1.
(If you’re not yet fully comfortable adding whole numbers, you might want to revisit the chapter on addition.)
What goes for addition is equally true of subtraction. To calculate 6.2 − 2.4, we set it up in columns like this:
Again the method is identical to that for whole numbers, presented in the chapter on subtraction. So we begin with the rightmost column, and borrow Is as necessary:
TRY THIS YOURSELF IN QUIZ 2.
Like addition and subtraction, multiplcation also translates easily to the decimal context. The main thing to watch out for is the position of the decimal point, or more accurately the positions of the digits relative to the decimal point. It is a good habit to think of the decimal point as being fixed and immovable, while the digits around it shuffle leftwards or rightward.
To see what we mean by the “position of the digits relative to the decimal point,” let’s look at the calculation 3 × 2, but with these digits in different places relative to the decimal point. Let’s start with 3.0 × 2.0. There are no surprises here, since this is nothing more than 3 × 2, which we know to be 6. Another easy one is 3.0 × 20.0 = 60, which we might calculate as 20 + 20 + 20 = 60. Alternatively, we could first work out 3 × 2, and then shunt the answer one column to the left, filling in the empty column with a zero, again giving 60. (This is the method presented in the chapter on multiplication.)
Next, what is 3.0 × 0.2? The answer is 0.6. We can see this easily, because 0.2 + 0.2 + 0.2 = 0.6.
But how does this fit in with the column depiction of the calculation?
The golden rule here is this: just as multiplying by 10 moves the digits one step to the left, so multiplying by 0.1 moves them one step to the right. Why should this be? One answer is that multiplying by 0.1 (that is to say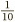 
) is the same thing as dividing by 10.
To calculate 3 × 20, the first step was to realize that 3 × 2 = 6, and the second was to shift everything one column to the left, filling in any empty columns with zeros, to arrive at 60. Calculating 3 × 0.2 is almost the same: first we calculate 3 × 2, and then shunt everything one column to the right, again filling any empty columns with zeros, to arrive at 0.6.
IF THAT SEEMS TO MAKE SENSE, HAVE A GO AT QUIZ 3.
The same line of thought works when we look at 0.3 × 0.2. As before we first work out 0.3 × 2, which is 0.6, and then shunt everything one step to the right, to arrive at an answer of 0.06.
With the golden rule in place, more complex multiplication can be put together just as for whole numbers. The pattern follows the column method for whole number multiplication exactly (so make sure you are comfortable with that before proceeding with this). To calculate 21.3 × 3.2, we would set it out like this:
We start on the right, by multiplying the whole top row by the rightmost digit on the bottom row. In this case, that means multiplying it by 2, and then moving everything one step to the right:
Then we move to the next digit of the second number, in this case 3, and again multiply the top number by that. This time no shunting, left or right, is required because 3 is in the units column:
Finally, we add up the two numbers below the line to arrive at the final answer:
NOW HAVE A TRY YOURSELF, IN QUIZ 4.
Notice how the decimal points are kept in line throughout the calculation. This is good practice, as it means all the columns marry up correctly.
We use decimals when we want a more accurate description than whole numbers can provide. But we may not always want the laser-sharp accuracy that decimals of unlimited length provide. This might sound strange, but think of it this way: do you need to know the quantity of butter to use in a cake, down to millionths of a gram? It is useful for me to know my weight to the nearest kilogram, or even in exceptional circumstances to the nearest gram, but never to the nearest nanogram (that is, 0.000000001g, or one billionth of a gram).
Very often we want to round decimals to some chosen level of accuracy. If I ask your height to the nearest centimeter, you might give me an answer of 1.64 meters. In doing so, you have rounded your answer to two decimal places.
Rounding is something we shall use throughout this book. So how does it work? We begin by specifying a level of accuracy, usually as a number of decimal places. The decimal places are the columns to the right of the decimal point: those representing tenths, hundredths, thousandths, etc.
Suppose we decide on one decimal place as a suitable level of accuracy for measuring the weight of a helping of dog-food. This means we will want to round our answer to the nearest tenth of a kilogram. The scale reads 3.734kg. So, when we round it, the answer is 3.7kg.
It is tempting to think that rounding is simply a matter of chopping the number off at a suitable point. Actually there is a little more to it than this—but just a little. For example, suppose we want to round 3.699 to 1 decimal place. Chopping the end off would give 3.6, but in fact 3.699 is much closer to 3.7. It is just 0.01 away from 3.7, whereas it is 0.099 away from 3.6. So 3.7 is the correct answer here.
Now, what if we wanted to round 5.46 to 1 decimal place? The two candidates are 5.4 and 5.5. But 5.46 is 0.06 away from 5.4, and just 0.04 away from 5.5, so 5.5 is the right answer. On the other hand, if we start with 2.13, then the two candidates are 2.1 (0.03 away) and 2.2 (0.07 away). So, this time, the answer is 2.1. Thinking about different examples like these produces the following rule:
• To round a number to a certain number decimal places, chop it off after those digits.
• Then look at the first digit of the tail (the part that was chopped off).
• If that digit is between 0 and 4, then leave the answer as it stands: just the original number, truncated.
• But if the first digit of the tail is between 5 and 9, then the final digit of the truncated number should be increased by 1.
This rule is, admittedly, a bit of a mouthful. But the procedure itself is not really very difficult, with a little practice. The trickiest case is when we have an example like 19.981, to be rounded to 1 decimal place. We begin by chopping off after 19.9. Then, the first digit of the tail is 8. So we know we have to increase 19.9 by 0.1 to 20.0. In this case the rounded answer doesn’t actually look anything like the original number, which might be confusing at first.
HAVE A GO AT QUIZ 5!
Incidentally, when rounding to one decimal place, it is good practice always to include that decimal place, even if it contains a zero. So in the above example, we would leave the answer as “20.0” rather than abbreviating it to “20.” The reason for this is that “20.0” communicates the level of accuracy to which you are working, namely one decimal place.
There will be plenty more practice in rounding later in the book.
Sum up If you can do arithmetic with whole numbers in columns, then it is only a small step to extend the technique to decimals.
1 Set out in columns and add
a 3.2 + 2.3
b 6.4 + 6.7
c 12.31 + 3.19
d 6.78 + 3.33
e 0.00608 + 0.00503
2 Decimal subtraction (columns again)
a 7.9 − 3.6
b 6.43 − 2.31
c 9.6 − 1.7
d 7.67 − 3.48
e 19.72 − 9.89
3 Digits move right
a 0.2 × 4
b 0.2 × 0.4
c 0.5 × 7
d 0.5 × 0.7
e 0.5 × 0.07
4 Full-blown multiplication
a 2.3 × 1.7
b 6.2 × 5.2
c 3.4 × 2.9
d 25.7 × 6.8
e 5.72 × 7.9
5 Round these.
a 5.3497 to one decimal place
b 0.16408 to two decimal places
c 0.16408 to one decimal place
d 9.981123 to one decimal place
e 0.719601 to three decimal places
