
• Interpreting fractions
• Recognizing when two fractions are the same
• Understanding top-heavy fractions
• Translating between fractions and decimals

Working with fractions ought to be easy. All it involves is cutting up cakes into suitably sized slices, and then counting the pieces. But somehow this simple idea can turn into a nightmare of “common denominators” and “lowest common multiples.”
There is one key thing to understand to be able to work with fractions. It is that any fraction, such as 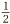 , can be rewritten in different ways, for example as
, can be rewritten in different ways, for example as  or
or 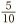 . The crucial question is this: how can we tell when two fractions are really the same? Might
. The crucial question is this: how can we tell when two fractions are really the same? Might 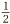 also the same thing as
also the same thing as 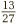 , for example?
, for example?
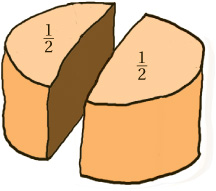
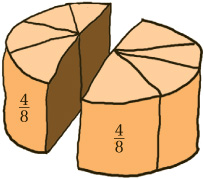
An old reliable method is to start with two identical cakes and divide up each according to the two fractions we are thinking about. If the two resulting helpings are the same, then so are the two fractions. So, if we divide one strawberry pavlova into eighths, for example, and serve up four of them, and divide another pavlova into two halves, and serve up one of them, then the two helpings are indeed the same. So, 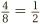 . But if we divide a cake into twenty-sevenths, and dish out 13 of them, we do not quite get a helping equal to half a cake. So
. But if we divide a cake into twenty-sevenths, and dish out 13 of them, we do not quite get a helping equal to half a cake. So 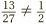 .
.
IF YOU HAVE GRASPED THIS, HAVE GO AT QUIZ 1.

What we need is a way to get this information directly from the numbers, without having to bake any cakes. As it happens, it is not too hard in this particular case: four eighths is the same as one half, because 4 is half of 8. On the other hand, 13 is not half of 27. This is fine, but some numbers are less easy to manipulate than 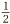 . What this is hinting toward is the golden rule which tells us how to change a fraction’s appearance, while keeping its value the same.
. What this is hinting toward is the golden rule which tells us how to change a fraction’s appearance, while keeping its value the same.
So, for example, 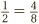 is true, because the second fraction comes from multiplying the top and bottom of the first fraction by 4. A less obvious example is that
is true, because the second fraction comes from multiplying the top and bottom of the first fraction by 4. A less obvious example is that 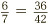 , as we can see by multiplying the top and bottom of the first fraction by 6. In terms of cakes, the golden rule tells us how to slice the helping of cake into thinner pieces, while keeping the overall helping the same size.
, as we can see by multiplying the top and bottom of the first fraction by 6. In terms of cakes, the golden rule tells us how to slice the helping of cake into thinner pieces, while keeping the overall helping the same size.
Here is some jargon: the top of a fraction is known as the numerator, the bottom is called the denominator. The golden rule says that if you have a fraction then multiplying the numerator and denominator by the same number may change the superficial appearance of the fraction, but not its underlying value. Now, this rule also works backward: if instead you divide the top and bottom by the same number, then the fraction’s value is similarly unaffected.
So if we start with a fraction such as 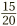 , and then we divide both the top and bottom by 5, we see the fraction in a new form:
, and then we divide both the top and bottom by 5, we see the fraction in a new form: 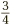 . The useful thing about this is that the numbers on top and bottom have become smaller. The fraction therefore seems simpler. This process of dividing top and bottom by the same number is known as simplifying the fraction.
. The useful thing about this is that the numbers on top and bottom have become smaller. The fraction therefore seems simpler. This process of dividing top and bottom by the same number is known as simplifying the fraction.
A nice thing about 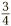 is that there is no number which can divide both the top and the bottom: this version of the fraction is as simple as it gets. We might say that it has been fully simplified.
is that there is no number which can divide both the top and the bottom: this version of the fraction is as simple as it gets. We might say that it has been fully simplified.
When writing a fraction it is usually good practice to present it in fully simplified form. This means checking whether there is any number which divides both the top and bottom, and if there is, then dividing top and bottom by it. So starting with 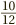 , we might notice that the top and bottom are both divisible by 2. Dividing top and bottom produces
, we might notice that the top and bottom are both divisible by 2. Dividing top and bottom produces 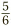 , which is now in fully simplified form.
, which is now in fully simplified form.
PRACTISE SIMPLIFYING FRACTIONS IN QUIZ 2.
The ultimate in simplification is when we have a fraction such as 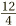 . Here the top and the bottom are both divisible by 4. Dividing top and bottom gives
. Here the top and the bottom are both divisible by 4. Dividing top and bottom gives 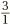 . But what is
. But what is 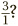 Well, it is 3 ÷ 1, which is 3. Whenever there is only a 1 on the bottom of a fraction, the bottom effectively disappears, leaving just the top on its own as a whole-number answer. (Going the other way, if we want to write 5 as a fraction instead of a whole number, we can just put a 1 underneath it, to get
Well, it is 3 ÷ 1, which is 3. Whenever there is only a 1 on the bottom of a fraction, the bottom effectively disappears, leaving just the top on its own as a whole-number answer. (Going the other way, if we want to write 5 as a fraction instead of a whole number, we can just put a 1 underneath it, to get 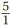 . The golden rule then tells us that this is the same as
. The golden rule then tells us that this is the same as 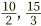 , and other variations on the theme. Notice that this matches our intuition, as 10 ÷ 2 and 15 ÷ 3 are indeed equal to 5.)
, and other variations on the theme. Notice that this matches our intuition, as 10 ÷ 2 and 15 ÷ 3 are indeed equal to 5.)
Most of the fractions we have seen so far in this chapter have had a smaller number on top of larger one. But there is no law that says it must be so: 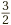 is a perfectly valid fraction too, and everything that we have said so far applies equally to “top-heavy” fractions like this (as does everything we say in the next chapter).
is a perfectly valid fraction too, and everything that we have said so far applies equally to “top-heavy” fractions like this (as does everything we say in the next chapter).
Most scientists don’t bat an eyelid at fractions like 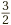 . But in the wider world they can seem a bit strange. Instead of saying “three halves of an hour,” most people would say “one hour and a half,” which might be written like this: 1
. But in the wider world they can seem a bit strange. Instead of saying “three halves of an hour,” most people would say “one hour and a half,” which might be written like this: 1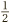 .
.
Expressions like 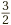 are accurately described as top-heavy, or, somewhat unfairly, as improper fractions. An expression like 1
are accurately described as top-heavy, or, somewhat unfairly, as improper fractions. An expression like 1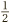 is called a mixed number. Notice that there is an invisible “+” sign here: 1
is called a mixed number. Notice that there is an invisible “+” sign here: 1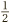 is really the same thing as
is really the same thing as 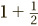 .
.
So much for the jargon. The point is that 1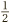 and
and 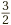 are actually the same thing. They are just presented in slightly different ways. The next challenge, then, is to be able to translate between the languages of improper fractions and mixed numbers.
are actually the same thing. They are just presented in slightly different ways. The next challenge, then, is to be able to translate between the languages of improper fractions and mixed numbers.
Suppose we are given a top-heavy fraction such as 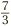 and we want to turn this into a mixed number. The process is not too tricky: in fact it comes directly from the meaning of a fraction. Don’t forget that a fraction represents division. So
and we want to turn this into a mixed number. The process is not too tricky: in fact it comes directly from the meaning of a fraction. Don’t forget that a fraction represents division. So 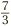 is exactly the same thing as 7 ÷ 3. Having said that, let’s calculate 7 ÷ 3. The answer is that 3 goes into 7 two times, leaving a remainder of 1. The 2 is the whole number part of the answer, and the remainder 1 then goes on top of the fractional part, while 3 goes on the bottom, giving
is exactly the same thing as 7 ÷ 3. Having said that, let’s calculate 7 ÷ 3. The answer is that 3 goes into 7 two times, leaving a remainder of 1. The 2 is the whole number part of the answer, and the remainder 1 then goes on top of the fractional part, while 3 goes on the bottom, giving 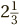 . (We saw this method in the chapter on division.) The general rule is:
. (We saw this method in the chapter on division.) The general rule is:
To express a top-heavy fraction (such as 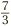 ) as a mixed number, the number of times the bottom fits into the top (2) goes outside the fraction as a whole number. The remainder (1) then stays on top of the fraction, and the bottom of the fraction (3) doesn’t change:
) as a mixed number, the number of times the bottom fits into the top (2) goes outside the fraction as a whole number. The remainder (1) then stays on top of the fraction, and the bottom of the fraction (3) doesn’t change: 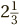 .
.
Going the other way is easier:
If we are given a mixed number (such as 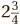 ) that we want to change into an improper fraction, then we start by multiplying the whole number (2) by the bottom of the fraction (4), which gives us 8. Then we add on the top of the old fraction (3), to get the top of the new one (11), and the bottom (4) stays the same. So the answer is
) that we want to change into an improper fraction, then we start by multiplying the whole number (2) by the bottom of the fraction (4), which gives us 8. Then we add on the top of the old fraction (3), to get the top of the new one (11), and the bottom (4) stays the same. So the answer is 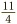 .
.
GOT IT? TRY QUIZ 3.
We have met two ways of expressing non-whole numbers: fractions and decimals. Since both of these languages are very common, it is important to know how to translate between the two.
The simplest examples are worth memorizing: 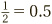 ,
, 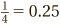 and
and 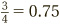 .
.
Beyond these, some techniques are required. Suppose we are given a decimal 0.4. How can we express this as a fraction? Actually, decimals are fractions already. Why is that? Well, remember that the columns to the right of the decimal point represent tenths, hundredths, thousandths, and so on (just as the columns to the left represent units, tens, hundreds, etc.). So 0.4 really is just 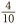 . All that remains is to simplify it, which we can do by dividing the top and bottom by 2, to give a final answer of
. All that remains is to simplify it, which we can do by dividing the top and bottom by 2, to give a final answer of 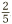 .
.
Let’s take another example: 0.35. We know 0.35 is three tenths plus five hundredths. Or, to put it another way, it is thirty-five hundredths: 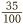 . We can simplify this by dividing the top and bottom by 5, to get
. We can simplify this by dividing the top and bottom by 5, to get 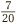 .
.
In the last example, 0.35 had two decimal places, so we had to express it in hundredths initially, before simplifying. Similarly, if we want to convert 0.375 to fractional form, we need to express it first as thousandths: 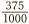 . The we can simplify by dividing the top and bottom by 5 three times, to get
. The we can simplify by dividing the top and bottom by 5 three times, to get 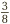 .
.
HAVE A GO AT THIS TECHNIQUE IN QUIZ 4.
Suppose we are given a fraction and want to express it as a decimal. First let’s take a nice friendly one, 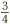 , and pretend that we don’t already know what the decimal equivalent is. How might we work it out?
, and pretend that we don’t already know what the decimal equivalent is. How might we work it out?
In the last section, before we simplified the result, the fractions we arrived at looked like this 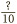 ,
, 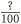 ,
, 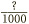 , and so on. If we can convert
, and so on. If we can convert 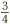 into a fraction of one of these types, then we will nearly be there. So we need to apply this chapter’s golden rule. We will try these possibilities in turn.
into a fraction of one of these types, then we will nearly be there. So we need to apply this chapter’s golden rule. We will try these possibilities in turn.
The bottom of our fraction is currently 4. But we want to change it to 10, or 100, or 1000, etc. Unfortunately, there is no whole number we can multiply 4 by to get 10. So we cannot express 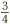 as tenths. Moving on, however, there is a number we can multiply 4 by to get 100, namely 25. So applying the golden rule, we multiply the top and bottom of
as tenths. Moving on, however, there is a number we can multiply 4 by to get 100, namely 25. So applying the golden rule, we multiply the top and bottom of 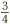 by 25 to get
by 25 to get 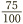 . It is now easy to recognize that this is the decimal 0.75.
. It is now easy to recognize that this is the decimal 0.75.
Now, we run into an awkward fact. Some fractions have decimal representations which look a bit strange. Start with 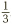 . If you type
. If you type  into your calculator, you should get an answer of 0.3333333333. In fact this is not an exact answer; the string of 3s really goes on forever. Try decimal short division for 1 ÷ 3 and see what happens!
into your calculator, you should get an answer of 0.3333333333. In fact this is not an exact answer; the string of 3s really goes on forever. Try decimal short division for 1 ÷ 3 and see what happens!
This is what is known as a recurring decimal, meaning that it gets stuck in a repeating pattern that goes on forever. A lot of fractions do this. For example, 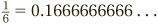
When calculating with these sorts of numbers, there is no choice but to round them off, after a number of decimal places, as the calculator does. However, there is a special notation for recurring decimals: a dot over the repeating number. So we would write 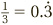 and
and 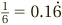 .
.
Some numbers have more complex repeating patterns. For instance 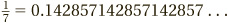 , which we would express as
, which we would express as 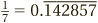 .
.
TRY EXPRESSING FRACTIONS AS DECIMALS IN QUIZ 5.
Every fraction will have an expression as either a terminating decimal (such as 0.51) or a recurring decimal (such as 0.51). There are other numbers where the decimal expansion goes on forever without ever repeating; these are the so-called irrational numbers. Famous examples are π (see Circles) and 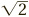 (see Pythagoras’ theorem).
(see Pythagoras’ theorem).
Sum up Once you have got to know them, fractions really are a piece of cake!
1 Different yet the same. Write 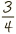 as:
as:
a Twelfths
b Eighths
c Sixteenths
d Twentieths
e Hundredths
2 Simplify
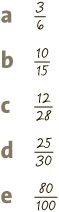
3 Top-heavy fractions to mixed numbers
 4 Decimals to fractions
4 Decimals to fractions
a 0.9
b 0.6
c 0.95
d 0.625
e 0.875
5 Fractions to decimals (possibly recurring)
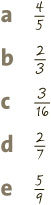
6 Which numbers on the bottom of fractions produce recurring decimal? Experiment and see!