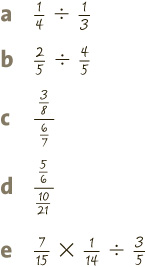• Knowing how to add and subtract fractions
• Canceling fractions, to speed up multiplication
• Understanding how to divide fractions
In the last chapter we saw how to represent numbers as fractions, noticing particularly that one number has many different fractional representations. In this chapter we will see how to do arithmetic with fractions: adding, subtracting, multiplying and dividing them.
Surprisingly, it is addition and subtraction which are trickier in this context: multiplication and division are fairly straightforward. A common error is to see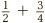 
and add the top and bottoms separately to get 
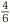. This is certainly wrong (think of half a cake being added to another three quarters of a cake). So let’s jump in at the deep end, and get started adding fractions the correct way.
EASY? TRY QUIZ 1.
Everyone can agree that adding fractions is easy, in some circumstances at least. What is one ninth plus one ninth? Two ninths, of course. What is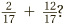 
It must be 
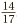. As long as you can add ordinary whole numbers, you can add these sorts of fractions. What makes these so simple is that these fractions all have identical bottom numbers. (In the jargon, they have a “common denominator.”)
The key to adding all fractions is to be able to transform any addition into an easy one like those we have just looked at. Take a simple example: what is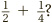 
Slicing up a cake quickly reveals the answer: 
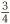. But we want a calorie-controlled way to see this directly from the numbers, skipping the cakes.
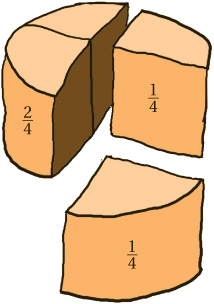
The crucial observation is that the half can be broken down into two quarters, using the previous chapter’s golden rule for fractions. Now we can rewrite the question. Instead of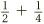 
we can write it as 
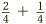. This brings us back to the familiar ground of fractions with the same bottom number, which we can then add straightforwardly. From this we get the golden rule for this chapter.
GET THIS TRICK? THEN TRY IT OUT IN QUIZ 2.
In the last example, we were able to split a half into two quarters. A similar trick will work with lots of other fractions. Suppose we want to calculate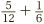 
. This time we can break the single sixth into two twelfths (using the previous chapter’s golden rule), and so change the question to 
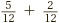. Once again we are back in the comfortable realm of matching bottoms! Another example is 
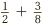. This time, we split the half into four eighths: 
.
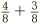A thornier type of problem is one like this: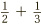 
. The trouble with this is that we cannot split a half into thirds, or a third into halves. Neither fits into the other. This time, to get to a sum in which the two fractions have matching bottom numbers we are going to have to alter both fractions. But which numbers should we multiply their tops and bottoms by? Let’s try some out. If we start with 
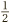, applying the previous chapter’s golden rule with 1, 2, 3, 4, 5 in turn produces the fractions 
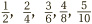, etc., all equal to 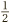. Meanwhile, starting with 
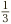produces 
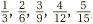, etc. Looking at these two sequences, we might spot that they both contain a fraction with 6 on the bottom. This is promising, as it allows us to rewrite 
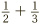as 
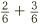, and then proceed as before.
Why did the number 6 work so well here? Looking at the bottom row of the sequence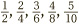 
, what we see is nothing other than the two times table. Similarly the bottom row of 
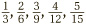is the three times table. The number 6 worked perfectly then because it features in both times tables. (In fact it is the first number to feature in both; this is the so-called “lowest common multiple.”)
So, when faced with the sum of fractions,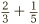 
, the first thing to do is to find a number which features in both the three and five times tables. Thinking about it, 15 is such a number. Then we can apply the golden rule twice, to turn 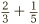into a sum of two fractions with 15 on their bottoms. To get 15 on the bottom of 
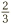, we must multiply by 5. So, according to the golden rule, we must multiply the top by 5 too: 
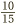. Similarly, to get 15 on the bottom of 
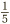, we have to multiply top and bottom by 3. This produces 
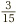, and our sum becomes 
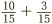, which we can easily finish off to get 
.
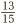The final step, when adding fractions, is to make sure that the answer is fully simplified, since this doesn’t happen automatically. For instance if we add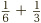 
, by following the rules above, we can turn this into 
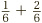, which then becomes 
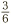. But 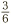can be simplified to give 
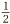, which is the final answer.
The rules for subtracting fractions are almost identical to those for adding them. The only difference is that, where previously we added, now we subtract. Genius! So, to take an example, if we have 
, then exactly as before we change this to 
. We can then evaluate it as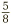 
. Since this can’t be simplified, we have finished.
PRACTISE ADDITION AND SUBTRACTION IN QUIZ 3.
If you are comfortable with adding fractions, then subtraction should be a piece of cake.
While adding and subtracting fractions is a slightly tricky procedure, multiplying them is straightforward. For instance, to calculate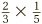 
all we do is multiply the numbers on the top (2 × 1), and the numbers on the bottom (3 × 5), and then put the answer back together: 
.
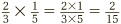The procedure may be easy, but what is actually going on, in the language of slices of cake? Well, suppose you have sliced a cake into fifths. Calculating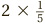 
would correspond to a serving of two such slices, amounting to 
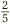of a cake. Similarly, the calculation 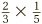gives the size of a serving which comprises 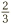of one those slices. As we have seen, this amounts to 
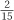of the whole cake. This is a case of multiplication being implied by one short English word: “of.” What 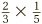really means is 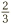of .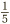
Of course, after multiplying fractions you may need to simplify the answer (as you also need to do when adding or subtracting them). In this case, though, a shortcut is sometimes possible.
To see how, let’s take another example: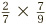 
. The rules for multiplying fractions (together with knowledge of times tables) make it simple to come up with an answer: 
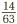. The final step is to simplify this fraction. So the question is: is there any number which can divide both the top number and the bottom number? A little reflection will reveal an answer: 7. So dividing top and bottom by 7 produces the final result: 
.
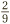That all worked perfectly well, but going back to the original question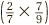 
we can actually see the final answer 
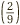immediately if we know how to look for it, without having to work through all the multiplication and simplifying.
The question amounts to this: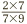 
. On the bottom of this fraction, even if we have forgotten all our times tables, we can see straight away that this number is divisible by 7. And the same goes for the top. So we can move directly to simplifying, by dividing out by 7 immediately, which we might write like this: 
.
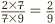This process is often known as canceling, and it is a great labor-saving device. It comes into its own when multiplying more than two fractions together. Suppose we are faced with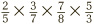 
. We can immediately set to canceling the 3 on the top with that on the bottom, the 7 on top with the one below, and similarly for the 5S: 
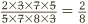. This can finally be simplified to 
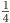. Once you get the gist of this, it is much easier than evaluating it as 
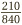, and then fiddling around trying to simplify it from there.
NOW HAVE A GO AT QUIZ 4.
As another example, take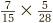 
. This time, the numbers on the top and bottom are all different. Yet some canceling is possible nevertheless. The 15 on the bottom is divisible by 5, which occurs on the top. So we can cancel those out, leaving 3 on the bottom (because 3 × 5 = 15). Similarly, we can cancel the 7 on the top with the 28 on the bottom, to leave 4 on the bottom 
.
When everything is canceled from one line, as happens on the top in this case, there is always an invisible 1 which remains. So the final answer in this case is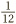 
.
What does it mean to ask what 10 ÷ 5 is? I’m not interested in the answer (that’s easy), but rather the meaning of the question. Well, the answer should be the number which tells us how many times 5 fits inside 10. To put it another way, the question we have to solve is 5 × 
= 10.
So far, so good. But what happens when we ask the same question of fractions: what is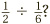 
According to the same philosophy, it ought to be the number of times that 
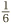fits inside 
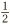. To put it another way, 
. The answer to this is 3.
This is all perfectly correct, but it is a common source of confusion that dividing one small number by another small number can produce something much bigger. Shouldn’t division always produce smaller results? The answer is a categorical “no”! Dividing by a large number gives a smaller answer, but dividing by small numbers (meaning smaller than 1) gives bigger answers.
To go back to 10 ÷ 5, it is no coincidence that the answer here is the same as the answer to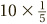 
. Why? Because 10 ÷ 5 means the same as
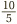as does 
.
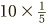What this suggests is the following rule for dividing fractions:
To divide one fraction by another, turn the second one upside down, and then multiply.
So we would write the above example out as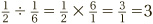 
.
Another example might be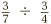 
. According to the rule for fractional division, this is equal to 
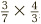, which, after canceling, becomes 
.
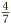NOW HAVE A GO AT DIVIDING FRACTIONS IN QUIZ 5.
A word of warning: sometimes fractional division can look very different, when the division symbol is itself replaced with a fraction. For instance, the last example might also be written as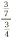 
. Don’t be put off by this—the meaning is exactly the same as before. And what if we saw something like 
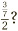Well this has the same meaning as 
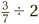, which is the same as 
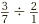, and so equal to 
.
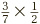Sum up Fractional arithmetic is a piece of cake, so long as you remember the rules!
1 When bottoms match
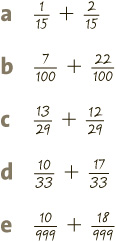
2 Mismatching bottoms
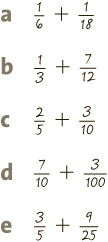
3 Double trouble
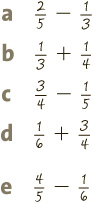
4 Cancel down first!
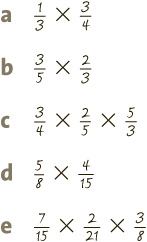
5 Fractions turn upside-down
