• Understanding proportions
• Translating between percentages, decimals, fractions and ratios
• Calculating percentages of quantities
Every time you open a newspaper, or watch the news on TV, there is a certain type of number that you are guaranteed to see. This is the percentage, indicated by its own little symbol “%.” What is a “percent”? It is a hundredth, nothing more, nothing less. To say that you have eaten 75% of a sandwich is exactly the same thing as saying that you have eaten 75 hundredths of it.
Percentages act as a convenient scale for measuring how much of something you have, with 0% meaning none of it, and 100% meaning all of it. Halfway along is the 50% mark.
We have already met another way of writing hundredths, namely decimals (see Decimals). The percentage 13% stands for thirteen hundredths, or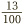 
and the decimal 0.13 means exactly the same thing.
As this example suggests, translating between percentages and decimals is straightforward. It is just a question of multiplying (or dividing) by 100, which simply means shifting the digits by two steps, relative to the decimal point. (Have a look at the chapter on decimals for a reminder of how to this works.)
So 99% is the same as 0.99, while 76% is the same thing as 0.76, and 8% is the same thing as 0.08. The last of these is the only one where a mistake might be made; you might think that 8% is the same thing as 0.8, rather than 0.08. But remember that the first column after the decimal point is the tenths column, and the second one is the hundredths column. As 8% means exactly “8 hundredths,” it must be equal to 0.08. On the other hand 0.8 represents the same thing as 80%.
The same system works even when the percentage itself has some decimal places, as in 64.3%. To change this to a decimal is simply a matter of moving the figures two steps to the right, relative to the decimal point: 0.643.
How much is 75% of a sandwich? Suppose your sandwich originally weighs 100 grams. Then it is easy to work out how much 75% is: 1% is the same as one hundredth of the sandwich, that is, 1 gram. So 75% is just 75 grams. If the sandwich was 200 grams, then 1% would be 2 grams, and 75% would be 150 grams.
Usually, of course, the figures are less neat than this. What if we want to work out 13% of a 267 gram sandwich?
To calculate 13% of 267, the first step is to translate 13% into a decimal: 0.13. The second step is then to multiply 267 by 0.13 (remembering that “of” means multiply). If we have a calculator, this is easy enough (otherwise we can use a method for doing it by hand; see Decimals).
Some calculators come with a special 
button. How does this work? Not very well, in my experience! I would advise against using it.
NOW CALCULATE SOME PERCENTAGES IN QUIZ 1.
Percentages are just one way of measuring proportion, that is, the relative sizes of two quantities. We have already met two other ways: decimals and fractions. If there are 25 people in a room, of whom 13 are female, what percentage does this represent? It is easy to represent this as a fraction: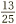 
of the people in the room are female. To convert this to a decimal, multiply top and bottom by 4 to get an equivalent fraction expressed in hundredths (see Fractions). This gives 
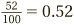. The final step, then, is to convert this to a percentage by moving the digits two places with respect to the decimal point: 52%.
IF THAT SEEMS STRAIGHT FORWARD, THEN TRY QUIZZES 2 AND 3.
It is important to be able to translate between the three languages of percentages, fractions and decimals.
Some of the most misunderstood statistics have to do with percentage increase and decrease.
Suppose that some new houses get built on my street, and 50 new people move in, raising the number of residents from 200 to 250. What is the “percentage increase”? Well, the increase clearly amounts to 50 people. So, to answer the question, we need to know what 50 is as a percentage of 200. Notice that it is 200, not 250, here: the increase is always gauged against the starting value. Well, 50 is one quarter of 200, which is 25%. So the population of the street increased by 25%.
The rule here is:
Percentage increase or decrease is the difference between the old and new numbers, as a percentage of the old number.
There is a warning which accompanies all these types of figures: they can feed into a brand of sensationalism beloved of newspaper headline writers.
Suppose your newspaper declares that “Cases of Hill’s disease up 400% this month!.” This sounds like a catastrophe in the making, conjuring up images of an epidemic exploding out of control. But the actual figures might be rather more prosaic. It might be that one person caught the disease last month, and five caught it this month. That corresponds to a 400% increase, and yet might be within the usual range of variation. If the average (that is to say mean, see Statistics) monthly figures are three cases per month, then last month was a little low, and this month is a little high without being a major cause for concern. Of course, taken across the population as whole (around 60 million in the UK), the risk remains vanishingly small. The lesson here is:
Warning! Percentage increases and decreases provide no information whatsoever about how widespread a phenomenon is!
NOW TRY QUIZ 4.
They are not even particularly useful in describing how the figures are changing, since an increase of 1000 cases might represent an increase of 200% (if the numbers have risen from 500 to 1500), or equally an increase of 0.1% (if the numbers have risen from 1,000,000 to 1,001,000). For these reasons, statisticians often complain about the overuse of “percentage increase,” and similar statistics. It would be more informative to report the actual figures, rather than sensational statistics.
Percentages provide one way to express proportions. Decimals and fractions are other possibilities. Now we will have a look at yet another.
Suppose I am mixing a cocktail, and a recipe tells me to mix orange juice and vodka in the ratio of 3:1. How do I know how much of each ingredient to pour? In particular, suppose I want the final drink to fill a 200ml glass. How much orange juice and vodka do I need?
A recipe might express this as combining “three parts orange juice with one part vodka.” This way of expressing the recipe gives a clue how to calculate the quantities. The crucial observation is that the mixed drink will consist of four parts in total.
Once we realize this, finishing off is fairly easy. The four parts in total should amount to 200ml. So one part must be 200ml ÷ 4 = 50ml. We want three parts of orange juice, which means 3 × 50ml = 150ml, and one part of vodka, meaning exactly 50ml.
Why did the recipe use the language of ratios instead of just saying 150ml juice and 50ml vodka? The answer is that ratios can easily be scaled up. If instead we wanted to mix a 2 liter jug of cocktail, the same ratio 3:1 remains valid, even though the exact quantities change. This time one part becomes 0.5 liter, so the final mixture is 1.5 liters of juice, and 0.5 liter of vodka.
Let’s apply the same line of reasoning to a more complicated ratio. Suppose another cocktail requires tomato juice, lemon juice and vodka in the ratio of 5:1:2. This time there are going to be eight parts in total, because 5 + 1 + 2 = 8. We could express the recipe as fractions: it should be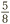 
tomato juice, 
lemon juice, and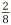 
vodka.
To convert a ratio into fractions, the rule is:
Add up the total number of parts in the ratio. This goes on the bottom of all the fractions, and the original numbers go on the top.
HAVE A GO AT WORKING OUT SOME RECIPES YOURSELF IN QUIZ 5.
If we then want to convert ratios into exact measurements, we multiply these fractions by the total quantity required. So if we want 2 liters of the tomato-lemon-vodka cocktail, we need to multiply 2 by each of the fractions 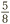, and 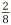, in turn, to get measurements of 1.25 liters tomato juice, 0.25 liters lemon juice, and 0.5 liter vodka.
One place that percentages commonly occur is as interest rates. Suppose you put $100 in a bank account that has an annual interest of 5%. Since 5% of $100 is $5, after one year, your account should have $105 in it.
What about after another year? A common mistake is to believe that, each year, the amount will grow by $5, producing $110 after two years. But the amount grows by 5%, not by $5. In the second year, it will grow by 5% of what was there at the beginning of the year, that is, $105. To work out 5% of $105 calculate 105 × 0.05 = 5.25. So, after two years, the account will contain $110.25. What about after 10 years?
To find the total at the end of a year, we first multiplied the amount of money at the start of the year by 0.05 and then added the result to the starting figure. A shortcut is to multiply the figure at the start of the year by 1.05. So, after one year, the account contains 100 × 1.05. After two years, it contains 100 × 1.05 × 1.05, that is to say 100 × 1.052. After three years, it contains 100 × 1.053, and so on. (Look at Powers if you need to remind yourself how these work.) So, to answer the question above, after 10 years, the account contains 100 × 1.0510, which comes out at around $162.89. (If the amount grew by $5 per year, after 10 years the account would contain only $150, so the difference is significant.)
In general, to calculate how much money an account contains, we need three pieces of data. First we need the original deposit made into the account. Call this M. Then we need to know the interest rate of the account, making sure this is expressed as a decimal larger than 1 rather than a percentage. (An interest rate of 5% or 0.05 would be expressed as 1.05; this means the original amount plus interest.) Call this number R. Finally we need to know how many years ago the deposit was made. Call this Y. The formula for the amount of money currently in the account is:
M × RY
IT’S TIME TO TRY THIS OUT FOR YOURSELF. HAVE A GO AT QUIZ 6.
Of course, if tax is deducted, the bank changes its rate, or money is moved in or out, then the story becomes more complicated! Nevertheless, this formula captures the fundamental rule of interest rates.
Sum up A decimal and a percentage are almost the same thing; you just need to multiply the decimal by 100. In the same way, ratios and fractions are almost the same thing. Beware: percentage increase or decrease does not tell us anything about the frequency of a phenomenon!
1 Work out each of these percentages as a number.
a Of a pack of 15 dogs, 20% are spaniels.
b In a factory of 400 workers, 77% work full-time.
c In a town there are 1225 roads, of which 32% are designated no-parking.
d In a colony of 134,550 ants, 88% are workers.
e A human brain contains 160 billion cells, of which 54% are neurons.
2 Express each of these proportions as a percentage, to the nearest 1%.
a A packet contained 22 sweets of which 7 are left. What proportion are left?
b An office has 86 workers, of whom 14 are off sick. What proportion are off sick?
c 197 of the 458 houses in a village are thatched. What proportion are thatched?
d In a city of 732,577 people, 118,504 are children. What proportion are children?
e In a country of 8 million people, 0.5 million wear glasses. What proportion wear glasses?
3 Convert these percentages to both decimals and fractions.
a 20%
b 100%
c 99%
d 5%
e 4%
4 Find the percentage increase or decrease.
a The number of people over 100 years old was 40 last year and 42 this year.
b The number of cars in my road was 31 last year and 38 this year.
c A girl is 0.74 meters tall one January, and 0.98 meters the same time next year.
d The number of DVDs sold is 13,488 in December and 11,071 in January.
e Cases of measles rose from 419 to 1012.
5 Work out the quantities for these recipes.
a Bread dough weighing 1kg is made from flour and water in the ratio 5:1.
b An exercise regime tells you to go 3 miles, jogging and walking in the ratio of 4:2.
c Cake mixture weighing 500 grams is made from eggs, butter and flour in the ratio 1:3:6.
d A drink of 360ml is mixed from fruit cordial and water in the ratio 1:8.
e A Spanish omelet weighing 440g is made from eggs, onions and potatoes in the ratio 5:2:4.
6 How much money do you have in each scenario?
a You put $200 in an account at 3% interest, for 5 years.
b You put $50 in an account at 4% interest, for 15 years.
c You put $3 in an account at 20% interest, for 10 years.
d You put $1000 in an account at 3.5% interest, for 30 years.