• Knowing what equations are
• Understanding what it means to solve an equation
• Getting to grips with techniques for solving equations
As we have seen, algebra is useful for expressing general rules. Its power lies in the fact that it remains true even when we do not know the values of all the numbers involved. In formulae the numbers whose value we don’t know are called unknowns. In some happy circumstances, a formula might contain enough information to pin down one of these unknown numbers. Then we can solve an equation.
TRY THINK-OF-A-NUMBER QUESTIONS IN QUIZ 1.
A good example of finding unknowns is a think-of-a-number game. Suppose I think of a number, and double it. If the answer is 6, then what is the number I first thought of? The answer, of course, is 3. But why? Because the unknown number was doubled to get 6. So, to find it, we work backward and divide 6 by 2. By doing the original calculation backward, we can find out where it started. This whole chapter is about how to turn calculations around, and undo them.
What we want is a reliable written method for tackling think-of-a-number questions, and their more sophisticated cousins. We need to think algebraically. So let’s return to the simple problem above, and call the original (unknown) number x. The idea is to find out its value. What we are told is that doubling x gives 6, that is, 2x = 6.
Now, we are aiming for an equation of the form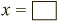 
, because that straightforwardly tells us the value of x. Currently, the left-hand side of our equation is not x on its own, but 2x. But if we halve that, we will get x alone, as we want. So that is the tactic.
Here is the key point: to keep the formula true, if we are halving the left-hand side, then we must also halve the right-hand side. So we halve 6 to get 3, and arrive at x = 3. We have solved the equation.
Of course, with such a simple example, this all seems very easy. But it illustrates some basic rules. Every equation asserts something. It says that its left-hand side is equal to its right-hand side. The nexus of the equation is the equals sign, which separates the left from the right.
The golden rule for this chapter is to keep the equation balanced. What that means is that if we divide one side by 4, or square it, or add on 32, then we must always do the same thing to the other side too, to guarantee that the equation remains true.
The same principles apply, even when the algebra becomes more complex. Suppose I think of a number, multiply it by 4, and then subtract 3. The answer I end up with is 17. What was my original number?
Have you worked it out? How did you do it? Try to reconstruct the mental steps which led you to the answer. The point is that the algebraic trickery we are using here is not magic. It’s just a formalization of the sort of reasoning that we can all apply quite naturally.
Let’s look at the last puzzle in more detail. The starting point is to translate it into algebra. We started with an unknown number: call it x. Then we multiplied it by 4 to get 4x. Next, we subtracted 3 to give us 4x − 3. Finally, we are told that this number is 17, which produces the equation:
4x − 3 = 17
As before, the aim is to turn this into a very simple equation of the form 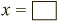, as this directly tells us the answer. With that in mind, the key is to undo the various steps, starting with the last one performed and working backward, until we end up with x on its own.
So, the first thing to do is to get rid of the −3. This means adding on 3 and, as always, we have to do the same thing to both sides. Adding 3 to the left-hand side gives just 4x, which is an improvement on 4x − 3, as it is simpler. Adding 3 to the right-hand side produces 20. So now we have:
4x = 20
IF YOU THINK YOU CAN MANAGE THAT, TRY QUIZ 2.
All that remains is to divide both sides by 4. Dividing 4x by 4 leaves x alone on the left-hand side, which is exactly what we were aiming for. Dividing 20 by 4 gives 5. So we end up with:
x = 5
One of the good things about equations is that you do not need anyone to tell you whether you have got it right. It is easy to check, and I would suggest that you always do this. If our solution above is correct, then if we take the original equation 4x − 3 = 17, and substitute in the value X = 5, we should get a true statement. If we don’t, then we know we have made a mistake. So let’s try: 4 × 5 − 3 = 17; this is true, so we have solved the equation correctly.
If we were presented directly with the equation 4x − 3 = 17, how would we know where to start: which move needs to be undone first? The two options are multiplication by 4 and subtraction by 3. An old friend comes to our assistance: BEDMAS (see The language of mathematics). That tells us that the multiplication was done first, followed by the subtraction. So, to undo these steps, we go in reverse order and tackle the −3 first.
Here is another think-of-a-number problem: I think of a number, treble it and subtract 2. The answer I get is the same as if I double my original number and add 4.
As usual, let’s call the mystery number x. If we treble it, we get 3x, then subtracting 2 gives 3x − 2. Now the problem tells us that this is the same as another quantity, which we get if we double x to get 2x, and add 4 to get 2x + 4. So the equation which encapsulates this problem is:
3x − 2 = 2x + 4
Now, as always, we are aiming for a final equation of the form 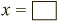. But, this time, things look trickier, as there are xs and numbers on both sides of the equals sign. The first step, then, is to improve this situation. We want to eliminate the xs on one side or the other.
The tactic is to collect together the xs on one side, and the numbers on the other. But how can we do this? Let’s deal with the xs first, and let’s decide to collect them on the left (we could equally well choose the right). That means getting rid of all the xs on the right. Well, there are two of them, that is to say 2x. We can eliminate these by subtracting 2x from the right. Of course, to keep the equation balanced, we also have to subtract 2x from the left:
3x − 2 − 2x = 2x + 4 − 2x
TRY COLLECTING LIKE TERMS IN QUIZ 3.
(It is not strictly necessary to write this step out; I am just doing it to make explicit what is happening.) Now on the right-hand side, the 2x and the −2x cancel each other out as planned, leaving only 4. On the left-hand side, we start with 3x and take away 2x, leaving just x. So our equation now reads:
x − 2 = 4
This is much simpler already, and now very quick to finish off. By adding 2 to both sides of the equation, we get the solution x = 6.
Let’s review that last example: we collected together all the xs on one side, and all of the plain numbers on the other. This technique is called collecting like terms, and it is the best way to make a complicated equation simpler.
NOW TRY QUIZ 4.
There are two other little tricks we might need. Firstly, if A = B then it is equally true that B = A. This means we can swap over the two sides of an equation any time we like. So if we find that 12 = 3x, we can easily swap the sides over and write this as 3x = 12. The second trick involves flipping +/− signs. We can do this so long as we follow the golden rule and do it to both sides. So if we have −4x = −8, we can flip the signs to get 4x = 8. Similarly, if we have −5x = 10, we can flip the signs on both sides to get 5x = −10.
The equation has a lesser-known cousin: the inequality. Here the nexus is not the equals sign (=), but one of the four inequality symbols. The first two are < and >, standing for “is less than” and “is greater than,” respectively. So we might truthfully write 4 < 7, or write × > 9 to indicate that x is some number larger than 9. These two symbols represent strict inequalities. (Alternatively you can think of these two symbols as being just one reversible symbol: 4 < 7 means the same as 7 > 4.)
The weak inequality symbols ≤ and ≥ stand for “is at most” and “is at least,” or “is less than or equal to” and “is greater than or equal to,” respectively. So, while it is true that 4 ≤ 7, it is also true that 4 ≤ 4. (But it is not true, that 4 < 4.)
With these symbols in place, we can write inequalities in the same way as we write equations. For example: 5x − 4 < 3x + 2. But what does it really mean to “solve” an inequality? We cannot hope for a unique answer. Instead, we want to pin down a range of values of x for which the original inequality is true.
If we follow the rules above, we first collect the xs on the left, by subtracting 3x from both sides: 2x − 4 < 2. Next we want to collect the plain numbers on the right, by adding 4 to both sides: 2x < 6. Finally we can divide by 2 to get out answer: x < 3. This is the solution to the inequality, and expresses the full range of values of x for which the original inequality is true. If x < 3 then it should be true, but if x ≥ 3, it should not. Test it out!
Solving inequalities is almost identical to solving equations. But there is a danger-point where the two diverge. If we find that 8 = 2x, then we can swap the sides of the equation to get 2x = 8. With an inequality, however, when we swap sides, we also have to reverse the inequality symbol. So 8 > 2x becomes 2x < 8.
There is another situation where the inequality has to be reversed. In the context of an equation, if we find that − x = −7, for example, then we can flip signs on both sides to positive, to get a final answer of x = 7. Let’s think about the inequality − x < −7. The value x = 8 does satisfy this, since −x = −8, which is indeed less than −7. Similarly the value x = 6 does not satisfy − x < −7, since −6 is not less than −7. If we simply flip the sign on both sides of the inequality − x < −7 (as we do with equations), we get x < 7. But we have just seen that this is not the right answer. The rule is that when you change the signs in an inequality (or, equivalently, when you multiply or divide both sides by a negative number) you need to reverse the inequality symbol. So, if we have − x < −7, we change the signs to positive on both sides, but in doing so we must also reverse the < symbol, giving an answer of x > 7.
SOLVE SOME INEQUALITIES IN QUIZ 5.
Sum up Solving equations occupies pride of place at the heart of mathematics, as this is the main tool for getting answers to algebraic questions. Just remember the golden rule: keep the equation balanced!
1 Solve these think-of-a-number problems!
a I think of a number, multiply it by 3. The answer is 18. What was my number?
b I think of a number, multiply it by 4, and then subtract 3. The answer is 25. What was my number?
c I think of a number, divide by 2, and then multiply it by 3. The answer is 9. What was my number?
d I think of a number, subtract 4, and then multiply it by 5. The answer is 20. What was my number?
e I think of a number, subtract 3, and then divide by 5. The answer is 5. What was my number?
2 Solve the problems in quiz 1 again, using algebra.
3 Solve these equations.
a 4x = 2x + 6
b 3x − 4 = 2x + 8
c 5x − 4 = 14 − x
d 2x + 2 = 12 − 3x
e 1 − x = 8 − 2x
4 Solve these equations.
a 2(x + 1) = 3x
b 3(x − 1) = 2(x + 1)
c 4(x − 2) + 2 = 2(x + 5)
d 4(2 − x) −1 = 2(x + 3) + 1
e 2(1 − x) + x = 3(2 − x) + 2
5 In quiz 3, try replacing the “=” sign with “<” and solving the resulting inequalites.