• Measuring angles
• Knowing the rules for calculating angles
• Understanding the geometry of parallel lines
This chapter contains truly ancient knowledge. Everything we shall see here was included in the greatest textbook of all time: the Elements, written by Euclid of Alexandria around 300 BC. It may seem surprising that Euclid’s geometry continues to be studied thousands of years later. But he got to grips with the root ideas of geometry: straight lines and circles, and the ways they interact. We will explore these in later chapters, including the many shapes that can be built from straight lines, of which the most important are triangles. But first we look at the fundamental geometrical notion of an angle.
An angle is an amount of turn. An ice skater or ballet dancer who spins on the spot might turn through a large angle. During a long journey, a car tire is likely to spin through a very large angle indeed! How do we measure angle? Well, just as distance can be measured in miles, centimeters or light-years, there are different units for angle too.
A common unit of turn is the revolution. If you stand on the spot, make one complete turn and end up facing in exactly the same direction as when you started, then you have completed one revolution. In engineering, the speeds of wheels and cogs are often discussed in terms of revolutions per minute (rpm). The second hand on a clock has a rotational speed of precisely 1rpm, while a washing machine drum might whizz round at 1000rpm.
An even more common unit is the degree. This is generally preferable when measuring small quantities of turn, less than a single revolution. One revolution is broken up into 360 degrees (usually written 360°). So if you turn on the spot until you are facing exactly backward, then you have turned 180° (that is, half of one revolution).
In many sports, such as skateboarding, ice-skating and diving, turning is an important ingredient. Typically, the amount of turn is measured in degrees. So a skateboarder might say that they have performed an “Ollie 180.” This means that they have turned 180°, that is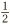 
a revolution. (What exactly an “Ollie” may be is a matter for another day!) Similarly a turn of 720° translates to two complete revolutions, because 720 = 2 × 360°.
In terms of the numbers, to translate from revolutions to degrees, we need to multiply by 360. So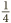 
revolution is, in degrees, 
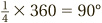. Going the other way, to convert degrees to revolutions we need to divide by 360. So, as we saw, 720° is 
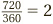revolutions.
GOT ALL THAT? NOW HAVE A GO AT OUIZ 1.
It is useful to practice translating between the language of degrees and revolutions (especially when talking to skateboarders!).
Here is some jargon about angles:
• An angle of 90° (or 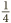revolution) is known as a right angle. Saying that two lines are perpendicular means that they cross at right angles. Also notice the little box we draw at the angle, to indicate a right-angle.
• An angle less than 90° is known as acute.
• An angle between 90° and 180° is called obtuse
• Angles between 180° and 360° go by the name of reflex.
There are various pieces of equipment we can use for measuring angles. One is a compass: not the device for drawing circles, but the type for finding North. If you want to know the angle a road makes to the North–South line, a compass will tell you. Compass bearings and angles are essentially the same thing.
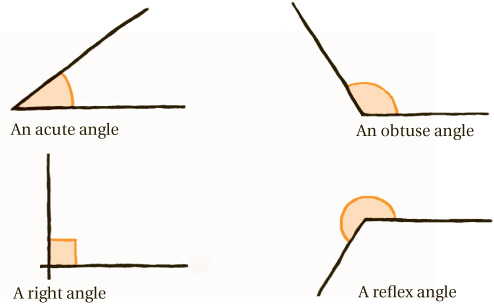
In the context of geometry, though, a more familiar (though lower-tech) tool is a protractor. It’s a semicircular piece of transparent plastic, with various markings on it: there is a base-line running along the flat edge and, at the center of this, a cross-hair; around the curved edge, angles are marked from 0 to 180°.
How do we use a protractor? If we have two straight lines which meet at a point, we might want to know the angle between them. What does this mean? imagine that the two lines are roads, and you are standing at the point where they meet, looking along one road. What we want to know is the angle through which you have to turn, so that you are looking down the other road (line). This is a task for a protractor! Lay it on top of the page, with its base-line lined up with one of the two lines, and with the cross-hair sitting exactly on the point where the two lines meet.
Looking at the curved edge of the protractor, you can see the numbered marks representing angles. The number at the point where the second line emerges is the number we want. Here is a warning though:
Warning! Protractors usually have two scales: one measuring angles clockwise, the other counterclockwise. Make sure you pick the one which counts up from 0°, not the one counting down from 180°!
We can draw angles by adapting this procedure slightly. If we want to draw an angle of 65°, say, the first thing to do is draw one straight line in the position that we want. Then, mark the point on that line where we want the second line to branch off (in this case this is at the end of the line), and place the cross-hair of the protractor on that point, with its base-line matching up with the drawn line. Next, find the 65° on the protractor (bearing in mind the warning above!) and make a mark on the page at that position. Finally, remove the protractor, and join the two marked points with a straight line.
IF YOU HAVE A PROTRACTOR, TRY DRAWING ANGLES IN QUIZ 2.
Look at this picture. It might be showing a road which is perfectly straight except at one point, where it has a corner. Where the two straight sections meet, there are two angles. Imagine that you are standing at the corner, in the middle of the road, facing along one section of road, and then you twist around, so that you are facing down the other. There are two ways you could do this: you could rotate clockwise or counterclockwise, and depending on your choice you will turn through a bigger or a smaller angle.
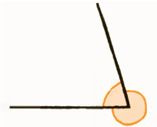
Now, these two angles are related in a precise way: if you turn through one, and then turn through the other, you will have turned one complete revolution. So, the golden rule tells us that, between them, these two angles add up to exactly 360°. This means that if we know one of them, say it is 72°, then we immediately know that the other must be 360° − 72° = 288°.
Angles like this are known as angles at a point, and this line of thought works just as well when there are more than two involved. We might think of the picture below as a junction of three roads. But again, the three angles must add up to 360°. So if two of them are 37° and 193°, we can immediately calculate the third angle (marked x) as 360° − 37° − 193° = 130°. No matter how many angles there are, the rule is:
Angles at a point add up to 360°.
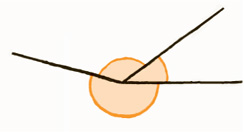
A similar argument works when we have a situation like the one opposite. This time we’ve got one straight road, maybe a motorway, and a turning coming off it. In this picture, though, the two marked angles do not add up to a full 360°. If you turn through one and then through the other, you have completed a half turn, which is 180°. Situations like this are known as angles on a straight line.
Angles on a straight line add up to 180°.
So as soon as we know one of the angles, say it is 35°, then we can calculate the other: 180° − 35° = 145°.
NOW HAVE A GO AT QUIZ 3.
When two perfectly straight roads cross each other, four angles are formed. Because these are angles at a point, the four must add up to 360°. But there is something else we can say too: if you look at the picture below, the angles seem to come in pairs: two large ones and two small ones.
This is not an illusion, in fact the two small angles must be equal to each other, as must the two large ones. These are known as opposite angles, and the rule is:
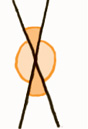
Opposite angles are always equal.
NOW IT’S TIME FOR QUIZ 4!
Why is this true? Well, one large angle together with either of the two small angles form angles on a straight line, and so must add up to 180°. That means that the large angle determines both of the small angles, each by exactly the same calculation. As soon as we know just one of the four angles, we can quickly work out all the others.
The notion of two lines being parallel is fundamental. It means that they can be continued forever, in both directions, without ever crossing. To say the same thing in a different way: the distance between two parallel lines is always the same, no matter where you measure it. Yet another way to say this is that the angle between parallel lines is 0°. In geographers’ terminology, they have the same bearing. Train tracks are a classic example of parallel lines.
In geometry, lines are indicated to be parallel by drawing matching arrows on them.
It is often useful to know when two angles are equal to each other. We have seen some examples above, namely opposite angles. Parallel lines also present situations where equal angles can be found. Let’s suppose we have a pair of parallel lines, and a third line which crosses them both (like a straight stick lying across a pair of railway tracks). In such a situation, there are two handy rules which tell us which of the resulting angles are equal.
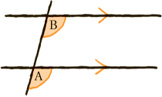
To start with, angles which are in identical positions, but on the two different lines, are said to be in corresponding positions. The first rule is:
Angles in corresponding positions are always equal. (Law of corresponding angles)
This should not come as too much of a surprise, since the two angles are identical in every respect, but are just in different places. Sometimes they are known as “F” angles, because the pattern looks like a capital F. (Don’t rely on this, though, as the F may be back to front or upside down, or otherwise deformed!)
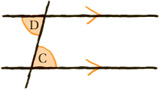
The second law of parallel lines and angles deals with the slightly subtler notion of alternate angles. Pairs of alternate angles lie on opposing sides of the third line, and are sometimes known as “Z” angles.
Alternate angles are always equal. (Law of alternate angles)
Why should this be true? It is a consequence of the laws on opposite angles, and corresponding angles. Try to see why!
Sum up Angles and parallel lines are the salt and pepper of geometry. Just remember how to combine them, and they will work wonderfully together!
1 Convert these angles from degrees to revolutions.
a 180°
b 360°
c 90°
d 270°
e 540°
2 Use a protractor to draw two lines that meet at each of these angles. Next to each angle write whether it is acute, obtuse or reflex.
a 45°
b 72°
c 83°
d 112°
e 229°
3 Sketch the following situations and calculate the missing angles.
a Two angles meet at a point. One is 75°. What is the other?
b Three angles meet at a point. One is 110°, another is 40°. What is the third?
c Two angles lie on a straight line. One is 60°. What is the other?
d Three angles lie on a straight line. One is 111°, another is 32°. What is the third?
e Four angles meet at a point. Three are 51°, 85° and 190°. What is the fourth?
4 Sketch the following situations (no need to use a protractor), and calculate all four angles. In each case, two straight lines cross, producing four angles.
a One angle is 90°. What are the other three?
b One angle is 45°. What are the other three?
c One angle is 21°. What are the other three?
d One angle is 122°. What are the other three?
e One angle is 176°. What are the other three?