Rochel Gelman
University of California, Los Angeles
Students of cognitive development no longer treat infants as passive receivers of inputs; it is generally assumed, rather, that infants are actively involved in the construction of their own representations. In the empiricist tradition, learning is the absorption of relatively unstructured input followed by the associative induction of the rules that give the input structure. In this view, the appropriate environment is an environment that repeatedly presents the items to be associated, such as words and their referents or fractions, and the kinds of things to which they may refer. In the constructivist tradition, by contrast, learning is the construction of a model of the world and is guided by model-building principles. These model-building principles may use as a basis of induction inputs that are not temporally or spatially paired and that are related in complex ways to the inductions drawn from them. Furthermore, some of these model-building principles may operate only during the construction of the initial stages of the model, causing the learner to attend to inputs and aspects of the structure of inputs that are not salient to the adult.
IN SEARCH OF A CONSTRUCTIVIST THEORY OF THE ENVIRONMENT
Given that children do not possess the adult model for a given domain of understanding and that the model-building principles that enable them to acquire that model do not focus on the aspects of the domain that are rendered salient by the to-be-acquired adult model, the kinds of inputs necessary to foster their acquisition of the adult model may differ dramatically from the kinds of inputs that seem relevant from the perspective provided by the adult model. This is an unsettling conclusion, in that it undermines our faith that we, as possessors of the adult model, can readily create the environments that will best foster its acquisition. In the constructivist view, we can create these environments only when we understand the inputs required by the model-building process. Two examples illustrate this problem: one about learning language and one about learning arithmetic. Both challenge commonly held views about the conditions under which children will or will not learn. In the first, children do learn, despite the expectation that they should not; in the second, children do not learn, despite the expectation that they should. As we will see, these expectations arise from an associative theory of the environment and its accompanying associative laws of learning. In contrast, expectations based on a constructivist theory of the environment yield accounts that are able to handle the findings.
There is More to a Supporting Environment Than Meets the Eye and Ear
If learners actively participate in their own knowledge acquisition, it is possible that they will use data to support learning of a kind that we either fail to notice or assume to be irrelevant for a given learning task. The nature of language learning and concept acquisition in blind and deaf children provides a case in point.
It is commonly assumed that children born with limited sensory abilities will not learn language normally. For example, it is assumed that the blind cannot learn the meaning of a word as normal children do—as a function of their seeing someone point to an object and/or and an action in the context in which a novel label is uttered, and then forming an association between the visual percept and the co-occuring spoken word. In the empiricist view, only the repeated exposure to such pairings permits an association to gain strength. The buildup of association networks makes it possible for the sound sequence to take on meaning.
A Language Acquisition Without the Sensation of Light or Sound. The foregoing characterization of the initial inputs for language learning has a long and distinguished history. In his discussion of the implications of blindness for his theory of concept learning, Locke, one of the intellectual fathers of empiricism, concluded that blind children would surely be at a disadvantage because they can not detect the patches of light that produce the sensations he took to be foundational. He reasoned that they should have more trouble learning language, in general, and visual terms, in particular. The related assumption that the requisite sense data for language production are provided by competent speakers has led many to conclude that the deaf do not learn language. Recent findings that blind or deaf children can and do master language force a reconsideration of these predictions. They also lead us to question the premise that primitive sense data serve as the starting point for the acquisition of linguistic and cognitive abilities.
Landau and Gleitman (1985) found that although blind children are somewhat slower than their sighted peers to start learning language, their mastery of syntax, vocabulary, and the functional uses of language is remarkably normal. Even as a preschooler, Kelli, one of their congenitally blind subjects, knew that sighted people can see. She would hold up an object when told to “Let mommy see the car” and hide an object when told to “Make it so mommy can’t see X.” She also turned around when asked, “Let me see your back” but not when asked, “Let me see your front.” She walked around solid, but not transparent, barriers when asked to show objects to sighted people, and so on. Although Kelli could not see at all, she learned English and, most importantly, she learned to use and understand “visual” vocabulary items like “look,” “see,” show,” and so forth. Her accomplishments point to the need to find a different account of the environmental variables that support learning. A similar conclusion follows from findings about language learning in the congenitally deaf.
Newport (this volume) reviews the evidence that language learning need not be tied to auditory inputs. We now know that the languages of the deaf are, like spoken languages, rich in structure for syntax, morphology, and phonetics (perhaps we should say ‘manetics’). Given that the deaf can learn language, the account of language learning cannot grant the sense data of sound a privileged status. Despite the considerable differences in the options offered by the visual and auditory modalities, the linquistic categories underlying the generation of sign languages map readily onto those governing spoken language. This means that theorists cannot take it as given that the equivalence class of relevant inputs for language learning is tied to a specific kind of sensory data. Indeed, Newport’s findings (this volume) on language learning in second-generation congenitally deaf children make it clear that the relevant inputs need not even occur in inputs from others, and that they can be generated by the young learner herself.
When second-generation congenitally deaf children are allowed to sign as soon as they can, their mastery of ASL typically exceeds that of their parents (Newport, this volume). Having started the language learning process relatively late in their development, during an era when signing was discouraged, the parents are more likely to use frozen signs than their progeny. Although the parents often do not decompose signs into morphological constituent units, their children develop fluent abilities to take apart complex signs in linguistically meaningful ways and recombine these in novel ways. Because the children also develop more advanced rules of syntax, they end up with a deeper mastery of the language than their parents. In this sense, we can say that they have learned more than was given in the input to them.
The deaf and blind children in the studies summarized here undeniably learned their language. Kelli was not born knowing the English sound–meaning correspondence si-SEE, anymore than a Spanish child is. Because the association theory of learning cannot handle Kelli’s mastery of visual terms and the syntax of English, we need to look elsewhere for a theory that can. Landau and Gleitman (1985) made an important contribution in this direction. They proposed that Kelli learned the meaning of “visual” verbs by using her existing knowledge of syntax and semantics to infer the meaning of verbs from the context in which they are used. Their account rests in part on the fact that verbs are choosy, that there are complex limits on the grammatical contexts in which a given verb can fit, and these contextual constraints are intimately tied to a verb’s meaning (Gleitman, 1990; Pinker, 1989).
In English, look can occur in verbal complements that start with purposive clauses like in order to; see cannot. We can say, “*John looked into the room in order to learn who was there” but not “John saw into the room in order to learn who was there.” We can also command someone to “Look!” but cannot command them to *“See!”. Or we can talk about “Looking through the glass carefully” but not *“Seeing through the glass carefully.” Syntactic and semantic principles govern these different use patterns of look and see. Because speakers’ utterances honor the constraints that these principles place on sentence generation, they offer learners the kind of patterned input that is relevant to inferring the classes of events to which these verbs refer. Interested readers should consult the Landau and Gleitman text for a fuller discussion of their account of how Kelli could have learned the meanings of look and see. They should also review the subsequent experimental work by Gleitman and her colleagues (e.g., Naigles, Gleitman, & Gleitman, in press) for evidence that young learners actually use such information.
Mental Structures Foster Learning of Structured Data and the Elaboration of the Structures Themselves. The lessons of the Gleitman line of work for our purposes should be clear. First, the correct use of visual terms like look and see can develop in the absence of sight. More generally, one need not assume that primitive sense data are the foundation from which language and concepts are developed. Second, because it rests on a structural description of the environments that can support the learning in question, the Landau and Gleitman account provides an important example of an alternative way to characterize the nature of relevant inputs for learning. It is an excellent case of a more general principle about the nature of supporting environments: What is relevant is best described in terms of the principles that organize the representations that a novice brings to a given learning setting. Inputs are relevant if they are structured in ways that are consistent with the interpretative principles implicit in the mechanism that will assimilate them. If the interpretative mechanism organizes data in terms of semantically and syntactically relevant variables, then relevant inputs are those that map onto these outlines. Because language samples provide instances of this class of data, it follows that these can serve novice learners, be the learner normal, blind, or deaf. In Piagetian terms, structures of mind are projected onto the environment. If organized interpretations are found, they, in turn, can serve to nurture growth in that structure.
The assumption that structures of mind are used to find or even create relevant examples of structured data frees us from requiring that the environment present in some simple and repetitive way the elements that are connected or intimately interrelated in the adult model. This is because the definition of relevance is given in structural as opposed to specific sensory terms. If patterns of sense data are structured as required, they can count as exemplars. But so can other patterns of input. In fact, our definition of relevance is neutral as to whether exemplars of the relevant class of inputs are in the environment or created in the mind of the child.
Because the mind can generate examples of relevant data (what Piaget called logical as opposed to empirical data) we have a way to start to explain how children could come to know more than is given in the data offered by adult models. Although there is no ready associationist explanation of how congenitally deaf children learn to use language better than their deaf parents—what is learned should be based only on what is given in the environment—a constructivist explanation can encompass such findings. As Karmiloff-Smith (this volume) puts it, not only do we assimilate structured data to growing structures of mind, we also come to explore the structure itself. This, in turn, leads to using what we know in novel ways.
In sum, language learning research with deaf and blind children provides compelling examples of how adult conceptions about the relevant inputs for acquisition can keep us from seeing what data our young actually do use. We can account for these children’s acquisition of linguisitic skill if we grant three premises: (a) young learners can themselves find the kinds of data that nurture their nascent linguistic structures; (b) young learners practice at applying and elaborating their knowledge; and (c) the definition of relevance is determined by the model-building process, not by the model that is to be built. Although these are consistent with a constructivist theory of mind, they are outside the conceptual framework of association.
Inputs for Learning May not Work as Intended
The structures that enable us to assimilate the data and concepts in a given domain, are, in general, a good thing; indeed, an indispensable foundation for the acquisition of knowledge. Structures of mind support the uptake and storage of data that can foster further developments of these structures; structured understandings enable us to transfer more readily and recognize common patterns among disparate surface characteristics, and so on. Still, these structures can also impede the acquisition of some kinds of knowledge. We are strongly inclined to assimilate data to the structures of mind we have, whether or not we have ones that lead to correct interpretations. This sets the stage for us to misinterpret the data, albeit no more on purpose than we intentionally perceive illusions. Just as we can think of illusions as overgeneralizations of the rules that govern our perception of constancies, so can we think of misinterpretations of novel data as overextensions of structures that are available. Gelman, Cohen, and Hartnett’s (1989) research on how young children interpret their school lessons about fractions allow us to expand on this aspect of a constructivist mind. It also allows us to develop the point that innate guidelines can both aid and hinder learning.
A Preverbal Knowledge Supports Learning about Natural but not Rational Numbers. I and my colleagues have argued that some mathematical abilities are based on innate sets of skeletal principles (e.g., Gelman & Meck, in press). When learning to use count words and to reason about cardinal numerosities, young children benefit from a set of preverbal skeletal counting and arithmetic principles. However, there is a downside to these innate contributions. Because they can foster learning about the counting numbers (the so-called natural numbers) and how to order, add, and subtract with these, they are ill-suited to support learning about other kinds of numbers. When they are applied to the data mean to start children down such learning paths, misinterpretations occur.
Why Learning about the Natural Numbers Should be Relatively Easy: Innate counting and arithmetic knowledge does not spare children from the task of learning the count words of their language; nor does it lead to perfect performances as soon as they start to talk. Rather, preverbal counting and arithmetic principles help children learn the relevant terms and how to use them in a meaningful way. Counting principles enable children to identify relevant linguistic data, that is, morphemes that are used in ways that are consistent with the constraints of the counting and arithmetic principles (Gelman, 1990a), much like incomplete templates guide the young white-crowned sparrow to selectively attend to its species-specific song. Although successful identification of the relevant input is an important achievement, it is but the first step along the way to skilled performance. It does not obviate the need to practice at the count words, anymore than does the opportunity to hear the right adult song at the right time in a bird’s development rule out its need to practice when its starts to sing. Fortunately, for children as well as birds, there is a potent tendency to engage in self-monitored practice. Just as white-crowned sparrows practice extensively (during the period of plastic song) to achieve a song that is consistent with that stored in their template, children work to master the count list and produce competent count sequences. That is, young children’s motivation to master the productions that employ what they have assimilated serves as a major source of learning opportunities.
These preverbal counting and arithemtic structures do more than encourage children to practice using the count words correctly. They also provide a structure that can support the development of mathematically meaningful understandings of the count words (numerlogs), graphic representations of numerosity (e.g., Arabic and Roman numerals or what prefer to call numergraphs), terms that refer to arithmetic relations, such as “more,” “less,” “equal,” and so on. The symbolic system of numerlogs and numergraphs for representing numbers is relatively easily assimilated to the preverbal system for representing numerosities and operations with them. We build on Gallistel and Gelman’s (in press) account of preverbal counting to develop this thesis.
The mental representatives of numerosity in Gallistel and Gelman’s (in press) model of preverbal counting are “blurs” on a mental number line; these blurs reflect the variability observed in numerosity discrimination studies with animals. Animals clearly discriminate on the basis of numerosity but they also have a strong tendency to confuse numerosities of approximately the same magnitude. The dimension of numerosity, like virtually all other psychological dimensions, approximates Weber’s law: The greater the numerosity, the more difficult it is to discriminate a given difference in numerosity (Gallistel, 1990). Although the model has these blurs overlapping in the representation of different numerosities, the preverbal counting process that maps from the numerosity of a collection to the preverbal representatives of numerosity (numerons) is inherently discontinuous. It steps from one blur to the next. Thus, the central tendencies of the blurs that represent distinct numerosities are not “pseudodense;”1 they do not lie one right next to the other on the mental number line; rather, they lie at separate intervals along this line. The numerlogs and numergraphs (“one,” “two,” “three,” or “1,” “2,” “3,” etc.) are also discrete. Thus, there is a straightforward one-one mapping of verbal and graphic morphemes to their separated counterparts in the preverbal system for representing numerosity.
The morphemes “one” and “1” map to the point on the preverbal number line that is the center of the blur that represents numerosity one, and likewise for “two” and “2,” “three” and “3,” and so on. In fact, the unequivocal discreteness (nonbluriness) of these morphemes reinforces the discreteness of the preverbal system for representing numerosity. And, the verbal and graphic entities behave in a way that conforms to the behavior of the entities in the system to which they map: they are ordered, as are the blurs on the mental number line, and they can be added and subtracted, as can the preverbal representatives of numerosity. The verbal algorithms employing the verbal counting process (counting up and counting down) enable the child to carry out these additions and subtractions at the verbal level (e.g., Fuson, 1988; Starkey & Gelman, 1982), aided by isomorphic operations with the preverbal representatives of numerosity.
Why Learning that Fractions are Also Numbers Should be Hard: Fractions, on the other hand, are in every way much more difficult to relate to the preverbal number system. First one has to come to terms with the fact that bipartite and tripartite symbols, “two”-“thirds,” “1”-“/”-“2”, and so on, must map to single entities in either the preverbal or, if already learned, the related verbal system—that is, to single points on the mental number line. The mapping of input to available representations is no longer one-one. For any adult who has forgotten how confusing this is, we recommend a course in complex number theory, in which the first great obstacle is to get used to treating the expressing “1 + 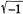 ” as a number, a single entity to be added, subtracted, multiplied, and divided just like “1” and “2.” Second, one has to come to terms with the fact that the fractions make the system of number pseudodense. The numbers no longer lie at separated intervals along the number line. One does not move by steps of significant magnitude from one number to the next; rather, the next number in the sequence lies infinitesimally close to its predecessor. Put another way, one cannot say what the distance is between one rational number and the “next” rational number, because there is no such thing as the “next” rational number. This is a structural feature of the “rational” number system that is not present in the “natural” number system, which is the only available structure to which the child can assimilate these weird beasts. Finally, there is no simple, counting-based verbal algorithm for comparing, adding, and subtracting these multipart symbols for the nonexistent “numerosities” that lie between one and two, three and four, and so on.
” as a number, a single entity to be added, subtracted, multiplied, and divided just like “1” and “2.” Second, one has to come to terms with the fact that the fractions make the system of number pseudodense. The numbers no longer lie at separated intervals along the number line. One does not move by steps of significant magnitude from one number to the next; rather, the next number in the sequence lies infinitesimally close to its predecessor. Put another way, one cannot say what the distance is between one rational number and the “next” rational number, because there is no such thing as the “next” rational number. This is a structural feature of the “rational” number system that is not present in the “natural” number system, which is the only available structure to which the child can assimilate these weird beasts. Finally, there is no simple, counting-based verbal algorithm for comparing, adding, and subtracting these multipart symbols for the nonexistent “numerosities” that lie between one and two, three and four, and so on.
In sum, although developing knowledge of the whole numbers can benefit from innately given skeletal counting and reasoning principles, the ability to learn that fractions are numbers cannot. For this reason, we have been exploring the possibility that young children will misinterpret their school lessons on fractions in ways that are dictated by the same principles that make it easy to learn the natural numbers.
LEARNING ABOUT FRACTIONS
Fractions are a watershed in pupils’ learning about mathematics. Assessments in the United States (e.g., Behr, Wachsmuth, Post, & Lesh, 1984; Carpenter, Corbitt, Kepner, Lindquist, & Reys, 1980) and England (Kerslake, 1986) reveal a persistent failure with rational numbers throughout elementary school and on into high school. Researchers in other countries converge on the same result (e.g., Nesher & Peled, 1986, in Israel). Hiebert and Wearne (1986) put it well when they concluded that, although many students acquire procedures for computing with decimals, they fail to develop a conceptual basis for understanding these. As a result, they end up with a series of procedures that work in some situations but not others. For example, although pupils correctly apply the computation rule “line up the numbers on the right [of the decimal point]” when adding numbers like 5.2 and 1.4, they run into trouble when adding 5.1 and .46. In this case, it is not clear how one should interpret “on the right.” Because there is no whole number “on the left,” Hiebert and Wearne expected students to treat the problem as it if were .51 + .46 or 5.1 + 4.6. Sixty-nine percent of the students in each of their fifth-and sixth-grade samples did just this when tested early in the school year.
The preceding studies of rational number knowledge have focused on pupils who are already half-way through elementary school or attending high school. We chose to work with younger children to determine if they assimilate inputs meant to support learning about fractions as if they were further food for their idea that numbers are what one gets when one counts things. If so, they should show strong predispositions to misinterpret data meant to exemplify alternative kinds of numbers.
The Gelman, Cohen, and Hartnett (1989) Study
Kindergarten and first-grade children receive some instruction about fractions. For example, in the United States where kindergarten classes use Scott and Foresman’s (1988) Invitation to Mathematics, they are taught about the number line and parts of wholes. The same series presents first graders with exercises on measurement and unit fractions, the latter being designed to teach children (a) the notion of N equal parts, where N = 2–8 equal parts of geometric shapes like circles, triangles, rectangle, and so on, (b) to match a written fraction (e.g., ½, ¼, and ⅓) to shapes cut into N equal parts, and (c) to master the vocabulary items of one half, one third, one fourth, one fifth, and one sixth. Gelman et al. (1989) interviewed a sample of kindergarten, Grade 1, and Grade 2 students toward the end of their school year to determine whether the children would misinterpret inputs designed to teach such items. Pupils attended one of several schools in greater Philadelphia area and came from an ethnically and racially diverse set of middle-class families. Because we wanted to present a variety of items, the children were seen individually, over several days (see Gelman et al., 1989, for details).
Misinterpretations of Non-Integer Numerals. Even the youngest children learned something about the data they encountered. When shown two cards, one with the symbol “½” and one with the symbol “¼,” 75% and 83%, respectively, of the kindergarten and first-grade children chose “½” correctly when asked to point to the card with one half. Although these children have correctly associated the verbal and numergraphic representatives of the first few unit fractions, they have not correctly integrated them into their system of arithmetic reasoning. When asked to choose which of ½ and ¼ was more, 13 of 16 kindergartners and 11 of 12 first-graders chose ¼. When asked to order the unit fractions, these children treated them as if they were natural numbers, with their magnitude proportionate rather than inversely proportionate to their denominators.
Our interpretation of the error is supported by children’s misreading of ½ and ¼. Although these children recognized the associations between the phrase “one half” and the numergraph “½” and the phrase “one fourth” and the numergraph “¼,” they did not read these two numergraphs correctly. Most commonly, they read them as if they designated two whole numbers (“one and two”), or they may have read a fraction as an arithmetic operation with whole numbers (“one plus two”), or as a multidigit number (“twelve”), and so on. Only two first graders even included the phrases “one half” and “one fourth” when reading the corresponding numergraphs, but they still gave bipartite renderings, reading “½” and “one and a half.”
Number Line Placement Errors. The Gelman et al. (1989) study included a series of “special number line” items. Different numbers of circles as opposed to integer numergraphs were placed at the points corresponding to the natural numbers. After an introductory discussion about relevant numerical terms and fractional expressions for parts and part-whole combinations, we started pretesting children for the placement task. Our “special number line” (4’4” long), schematized in Fig. 10.1, was opened up, and children saw one and three circles (all 4.75” in diameter), placed where the integers 1 and 3 would have been. Pretest questions served to assure that children (a) fill in the missing whole number with two circles, (b) tell us what numerical values were represented by the circles (c) rank order these representations, (d) tell us what numerical values could be represented to the left of “one” and to the right of “three” after those already shown on the line, and (e) correctly use the terms for fractional parts and part-whole combinations of circles. Some background on the task and data analyses introduces our discussion of the findings. The placement task was administered in a five-phase sequence, spaced across several days, to provide children with ever more relevant clues about the correct placements. On all trials, a child’s task was to put each test display below the point on the line “where it belonged” and then explain why it went there. A sample fraction placement trial is shown in the bottom half of Fig. 10.1. During Phases 1 and 2, children received no hints. These phases differed mainly in terms of the values of the test displays (1½, 1⅓, and 1¼ circles in Phase 1; ½, ⅓, and ¼ of a circle in Phase 2). Therefore, we can combine the data from these two phases to see how children first related these fractional numerosities to those given by the number line. Each child’s pattern of responses across the six Phase 1 and 2 trials fell into one of the following categories:
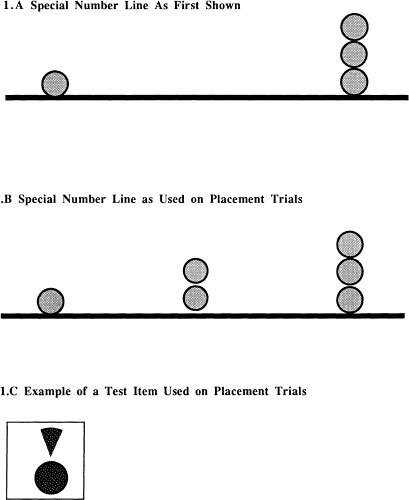
Fig. 10.1. Schematic representations of the special number line when it was first shown (1. A) and during testing (1. B) as well asan example of a test placement item (1. C) in Gelman, Cohen, and Hartnett (1989).
1. Correct (At Least 50%). Children’s placements correctly integrated metric ordering of the fractional parts and whole circles on at least three of the six trials in Phases 1 and 2.
2. Parts Alone Rank Ordered. Children’s placements neglected the whole circles; the relative sizes of the parts were ordered without regard for the positions of the whole numbers. For example, one child placed 1¼ circles at “1,” 1⅓ circles at “2,” and 1½ circles between “2” and “3.”
3. Whole Number Placements. These involved one of two counting strategies. Some children placed test displays as if they had counted the number of separable parts. For example, several put 1½ circles at “2” and all of ½, ⅓, and ¼ circles at “1.” Others simply counted the whole circles and ignored the parts and therefore placed the preceding items at either “1” or “0.” These responses fail to recognize the fractional character of the numerosities that the parts of circles were meant to instantiate.
4. Others. All response patterns that differed from the preceding three were coded in this category. For Phases 1 and 2 these included those where children placed successive test displays from left to right, put each test item at a different position without any concern for order, or generated sequences that we could not decode. Because we do not discuss the additional response biases that occurred once the experimenter began to show children where to put displays containing one half of a circle (during Phase 3), they are not described here.
The distribution of the percentage of children who used each of preceding response patterns during Phases 1 and 2 of the placement test is shown in Fig. 10.2. Only 3 of the 28 children in kindergarten and Grade 1 correctly interpreted as many as half of the test displays. Sixty-three percent and 42% of the children in these respective grades were whole number responders, an outcome that adds weight to our proposal that these young children would not treat the test displays as if they represented ordered points between whole number points on the line. That is, they gave no evidence of knowing that rational numbers are what we have termed “pseudodense.” Instead, as expected, they were much inclined to find ways to treat exemplars of fraction and whole number combinations as if they were all representations of discrete whole numbers. Furthermore, as reported in Gelman et al. (1989), these initial misinterpretations resisted our hints. The only children who benefitted from such hints were correct on at least 50% of their initial Phase 1 and 2 placement trials, suggesting that they already had some insight when the interviews began.
The Second Graders in Gelman et al. Because the second graders in Gelman et al. had another year of schooling to learn about the test items we used, they should outperform the younger children. To a certain degree, they did. Half of them read ½ and ¼ correctly, and 58% were scored correct on the number-line task. However, only 42% selected ½ as more than ¼; and even fewer (33%) selected 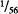 over
over 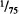 . This pattern of results for the second graders suggests that they memorized some things about ½ and ¼, but still had little understanding of these as fractions. This conjecture gains support when we consider how these children answered when asked whether there were numbers between 1 and 2 and between 0 and 1. Five of the 12 children allowed that there was one number between 1 and 2; only three were as generous when they considered whether there are numbers between 0 and 1. Our next study provides more evidence that second graders have a way to go to achieve an understanding of the relevant symbol system.
. This pattern of results for the second graders suggests that they memorized some things about ½ and ¼, but still had little understanding of these as fractions. This conjecture gains support when we consider how these children answered when asked whether there were numbers between 1 and 2 and between 0 and 1. Five of the 12 children allowed that there was one number between 1 and 2; only three were as generous when they considered whether there are numbers between 0 and 1. Our next study provides more evidence that second graders have a way to go to achieve an understanding of the relevant symbol system.
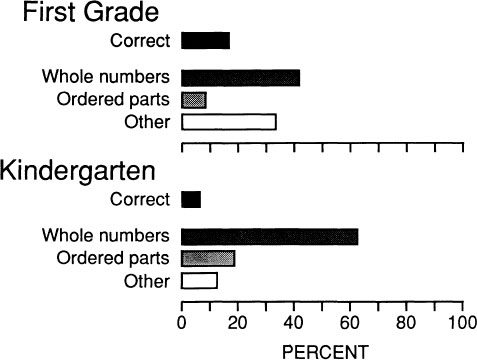
Fig. 10.2. Percent children in the Gelman, Cohen, and Hartnett (1989) Kindergarten and Grade 1 groups whose initial placements were correct or not. Incorrect placement patterns are broken down to show the percent of children who used a whole number or some other strategy.
The Cohen, Gelman, and Massey (in preparation) Follow-Up Study
In this study children were asked to read representations of less familiar fractions, 1⅓ and 1¼; to point to which of these was “more”; and explain their choices. Pupils from kindergarten and Grades 1 and 2 were tested individually at the end of their school year. They were at a somewhat higher socioeconomic level than the pupils in Gelman et al. (1989). Summaries of the data are presented in Table 10.1.
TABLE 10.1
Percent Children In Follow-Up Fraction Study Who Correctly Read 1⅓ and 1¼; Correctly Choose 1⅓ as more than 1¼; and Do Not Explain Their Ordering Choices by Comparing Whole Numbers
Grade |
Percent Correct Readings |
Percent Correct More Choices |
Percent Who Do Not Give Whole Number Explanations |
K |
0 |
0 |
20 |
I |
30 |
20 |
20 |
II |
20 |
20 |
10 |
Perhaps the most salient result of this study is the absence of grade-level effects. Almost none of the children in the study were able to order and read 1⅓ and 1¼ correctly. Additionally, their justifications for ordering the fractions the way they did repeatedly involved talk about whole numbers, especially that 4 is more than 3. Samples of what children said when they were reading and justifying their choices of 1¼ over 1⅓ are given in Table 10.2. The older children are somewhat more articulate. Still, the large majority of them clearly treat the symbols as representations of whole numbers. Therefore, it seems that whatever second graders know about how to read and order questions about ½ and ¼ is not used with 1⅓ and 1¼. Even after two grades of instruction with items like these, their tendency to apply natural number interpretations inappropriately remains strong.
Learning Can Occur
We could marshall further evidence that young elementary-school children misinterpret inputs designed to teach them about fractions and how their tendencies to interpret data about fractions is assimilated to their assumption that all numbers are count numbers. Still, we do not want to dwell too long on this, given that the record shows that many students are able to master rational numbers. Some clues as to how this happens come from a questionnaire study that Patrice Hartnett and I were able to conduct with Grades 2 through 8 pupils in several schools of the Ocean school district. The district is in a Midwestern suburb of the United States and serves both a broad range of the middle class as well as some lower-class homes.
The Hartnett and Gelman Questionnaire Study. Questionnaires were administered to Grades 2, 3, 4, 5, 7, and 8 classes, Grades 2–3 and 4–5 gifted classes, and a pre-algebra seventh-grade class. The school system identifies and places children in a “gifted” track at an early age; in the seventh grade, they are enrolled in a pre-algebra course. On the advice of a mathematics curriculum expert in the Ocean district, pupils in the regular second and third grades answered a simplified version of the questionnaire that was administered to all other pupils. These second and third graders performed as expected when asked which of ½ and ¼, and ⅞ and 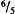 , was more; that is, only 47 and 27 percent correctly chose ½ and
, was more; that is, only 47 and 27 percent correctly chose ½ and 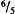 as more. Because we will see that the gifted Grade 2–3 students had similar inclinations, we will use their data as a baseline in evaluating whether learning occurs.
as more. Because we will see that the gifted Grade 2–3 students had similar inclinations, we will use their data as a baseline in evaluating whether learning occurs.
TABLE 10.2
Examples of How Children in the Cohen, Gelman, and Massey Study Read and Explained their ordering of 1⅓ and 1¼
Grade and Subject No. |
How Fractions Were Read |
Responses To Order Question |
|
|
Order Choice |
Explanation of Choice |
Kindergarten |
1. one, one three;
One, one four |
1¼ |
four is more than three |
|
2. One plus three;
One plus four |
1¼ |
4 + 1 = 5 and 1 + 3 = 4 |
|
3. One minus one plus three;
One minus four |
1¼ |
cause there’s a four |
|
4. One plus a one plus three;
One plus four |
1¼ |
cuz four on the bottom and three on the bottom |
Grade 1 1. |
1. One and a third;
One and a quarter |
1⅓ |
like ‘regular’ ⅓ & ¼—it’s still bigger with the one since they both have it |
|
2. One hundred and thirteen;
One hundred and fourteen |
1¼ |
three is less than four; same thing in the 100’s |
|
3. Eleven three;
Eleven four |
1¼ |
it has one number higher underneath |
|
4. One third;
One fourth |
1¼
1¼ |
three comes before four; lower when you count |
Grade 2 |
1. Three and a halt;
Four and a half |
1¼
1¼ |
three comes before four |
|
2. One third;
One fourth |
1⅓ |
¼ has a smaller piece than a ⅓ |
|
3. Three and a half;
Four and a half |
1¼ |
four is bigger than three |
|
4. Three-one-one;
One-one-four |
1¼ |
that has four and this has three |
The Effect of Kind of Class and Grade Level. Figure 10.3 summarizes the data from the “which is more” battery of items. Data from the regular Grades 4 and 5 are combined to facilitate comparison with the combined Grade 4–5 gifted class. It can be seen that giftedness influences these children’s ability to order numergraphic representations of fractions. By Grades 4 and 5, the gifted grade 4–5 pupils do better than their agemates in the regular Grade 4 and 5 classes. Indeed, they do about as well as the children in the regular Grades 7 and 8. Further, although all of the gifted students in Grade 7 always made the correct ordering choices, some students in the regular Grade 7 and Grade 8 classes did not, especially when comparing .65 and .8. The preference for .65 here is consistent with a bias to ignore the decimal point and read these items as if they were the natural numbers of 65 and 8.
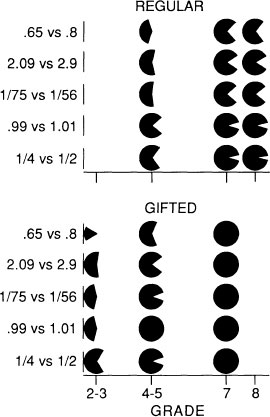
Fig. 10.3. Percent correct orderings (schematized as proportion of filled-in circles) as a function of grade (or grade combination), pair of test items, and class kind. Note that a half-filled circle represents the 50% level. If less than this is filled in, there was a bias to answer on the basis of the value of the whole numbers.
The gifted seventh-grade students were also more inclined to give unusual answers to our request for a number between 3 and 4. Forty percent gave answers such as 3.7, 3.0000000000000000001, 3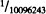 and 3.276542169, as opposed to the obvious answers of 3½ or 3.5. This contrasts with the 10% and 5% of the pupils in the regular Grades 7 and 8 classes who wrote something other than 3½ or 3.5. To our surprise, there even were students in these later grades (5% and 17%, respectively) who either denied that there were any numbers between 3 and 4, wrote a whole number like 2, or skipped the item.
and 3.276542169, as opposed to the obvious answers of 3½ or 3.5. This contrasts with the 10% and 5% of the pupils in the regular Grades 7 and 8 classes who wrote something other than 3½ or 3.5. To our surprise, there even were students in these later grades (5% and 17%, respectively) who either denied that there were any numbers between 3 and 4, wrote a whole number like 2, or skipped the item.
Novel answers to a question about numbers between whole numbers are of special interest. Just as the ability to generate novel instances of sentences can index mastery of the structure of language, so can the ability to generate nonconventional, numerical answers index mathematical understanding. Children who generated items with lots of zeros or decimal places seemed to be telling us that they were well on the way to understanding a key property of the rational numbers, that is, that they are what we call pseudodense.
Consideration of why children said there are two numbers in a fraction adds weight to this suggestion that at least some children had begun to develop a new mathematical understanding of why fractions are numbers. Sixty-two percent of the pupils in the regular 4–5 classes gave answers that were irrelevant, such as, “I forgot” or tautological, such as, “Because if there weren’t 2 numbers then you couldn’t have a fraction” or “Because you have to have a denomonator and numorator.” Although they were no less likely to contain spelling errors, the answers given by the gifted fourth and fifth graders were qualitatively different than those offered by the regular fourth and fifth graders. For example, one gifted fourth grader wrote, “The dnmunator is the hole, the numirator is how many peices you have of the hole.” Another wrote, “One of the numbers stands for how many thimes something is divided up into and the other how many are taken.” Further, none of the gifted children in either Grades 4–5 or 7 offered tautological or irrelevant answers. This contrasts with the 41% and 44% of the regular seventh and eighth graders who did, sometimes in ways that revealed competition from their algorithm lessons on fractions. For example, one eighth grader wrote, “One is a numerator and one is a denominator. We need both numbers to figure out the answer.” Similar bits of algorithmic ideas showed up occasionally in some of the wrong answers that others in these classes gave us, such as, “If one number then you could not add or subtract.”
The gifted Grade 2–3 children’s answers to this question as well as that about numbers between 3 and 4, leads to the conjecture that this group was learning something about fractions as a kind of number—even though they failed the ordering tasks. Only 39% of the youngest gifted children wrote answers that were wrong—either because their answers were tautological or unacceptable—to explain why there are two numbers in a fraction. Examples of wrong answers included “Who knows?”; “Because if there were one 1, then know one could tell what it is.” Examples of more felicitous answers from these children included: “It explanes how meny out of how meny”; “To tell what the amount that your taking away from”; and “Because you have to talk the whole thing and how much of that your using.” In addition, only 4% of these young gifted children denied that there were numbers between 3 and 4. Most wrote the conventional answer of 3½ (using either numerlogs, numergraphs, or some combination of both as in “3 and a half”) as an example of such a number; a few even gave somewhat novel answers, like 3¾. Not only does this contrast with the kinds of answers the older children in the Regular grades offered, it contrasts with those given by the second graders in Gelman et al. (1989). The Gelman et al. sample had a strong tendency to deny the presence of such entities. Thus, although the younger gifted children also fell prey to a tendency to order noninteger numergraphs as if they were comparing whole numbers, they nevertheless had begun to acquire some knowledge about fractions being a different kind of number than the integers.
An ongoing study in my lab rules out the possibility that these young gifted children always had some intuition about the nature of fractions. We are finding that a sample of kindergarten children who, on average have IQs over 120, are no more likely to do well on items like those used by Gelman et al. (1989) than are children who, on average, have IQs around 100. Hence, we have the problem of explaining how any child, gifted or not, begins to learn about the numberhood status of fractions. If it really is the case that a constructivist mind interprets novel data in terms of what is already assumed and/or known, how could this ever happen? We will return to this question.
LESSONS FROM COMPARING AND CONTRASTING LEARNING ABOUT LANGUAGE AND FRACTIONS
Our account of why children “fail to learn” about fractions is identical in form to the account of why blind and deaf children do learn language. In the case of fractions, children interpret the inputs as if they were further data for the theory of number embodied by the kind of knowledge structures they have in this domain. They “overgeneralize” their counting principles and produce a distorted assimilation of the instructional data to an implicit theory of number that cannot handle these data as we, the instructors, intend them to be handled. Here, as in the language cases, the children use whatever structures they have to sort the environment and to interpret what they attend to.
Although the two cases yield comparable conclusions about the limits on our current ability to know what inputs will nourish concept development, the lessons they offer are not always identical. This is because we compared learning at different points in development. We also used an example that highlights how innate guidelines can both aid and hinder learning.
Although the ability to develop knowledge of the whole numbers benefits from innately given skeletal sets of counting and numerical reasoning principles, the ability to master fractions does not. Available counting and reasoning principles serve learners in their active search for inputs that are relevant to number and their efforts to learn the mathematical meanings of the count words as well as relevant mathematical symbols. In fact, we contend (e.g., Gelman & Cohen, 1988) that these principles are why normal people in many different cultures and settings can and do learn both to count with understanding and to solve whole number addition and subtraction tasks—whether or not they receive formal instruction (Carraher, Carraher, & Schliemann, 1985; Lave, 1988; Resnick, 1988; Saxe, Guberman, & Gearhart, 1987; Saxe & Posner, 1983). However, there is a price we pay for this fluent ability to develop an understanding of whole numbers. Such innately based knowledge can stand in the way when we turn to learning more mathematics. This seems to be the case when we turn to learning the rational numbers, a fact that helps sharpen the questions we should ask about the nature of supporting environments and learning. Because many individuals do go on to learn that fractions are numbers and even more advanced mathematics, we have two major tasks. The first is to spell out the kinds of conditions that support learning based on innate skeletal principles. The second is to account for our ability to acquire concepts that gain their coherence from structures other than those that have an innate base.
SOME CONSTRUCTIVIST IDEAS ABOUT LEARNING
Early Learnings
How Innate Contributions Support Learning. Our account of much early language and concept development starts with two basic assumptions: First, such learning can benefit from domain-specific sets of nonverbal principles. Second, these skeletal sets of principles support the search for, and the coherent uptake of, data that nurture further knowledge acquisition in the domain they define. (See Gelman, 1990a, 1990b for the development of this argument for young children’s learning of how to use verbal counting principles as well as the animate-inanimate distinction.)
It used to be assumed that if one said something is innate, they meant it was not learned, and vice versa. This cannot be assumed today, for contemporary developments in the study of animal learning have contributed to the findings that innate, domain-specific structures can actually provide the foundation for learning, and the course of such learning is not immutable. Put differently, it simply is not true that whenever innate factors contribute to complex behaviors, these will appear full-blown—as it were, from the head of Zeus—as soon as a “triggering” stimulus is presented. The course of learning is jointly determined by the innate learning mechanisms and the vagaries of experience. In fact, it is unlikely that genetic contributions to a behavior will be seen if the organism is deprived of the necessary opportunity to deploy the learning mechanisms that lead to it. Marler’s series of studies on the nature of birdsong learning (this volume) provides lovely evidence for these points, starting with his conclusion that white-crowned sparrows acquire their song as a joint function of instinct and learning mechanisms. (See also Gottlieb, 1983, for relevant discussions of genetic programs and their influence on both learning and the role of environment.)
Young male white-crowned sparrows must encounter the adult song at the right moment in a sensitive period, otherwise they will not grow up to sing the adult song. These experiences contribute to the development of the correct representation of their parents’ dialect of the species’ song. In Marler’s terms, they provide the inputs needed to fill in and tune the young birds’ innate templates. Still, these early encounters do not suffice to guarantee an error-free outburst of the correct song in adulthood. Just as is true for the acquisition of complex human skills, an extended period of practice must occur first. During the young bird’s period of plastic song, what is first sung has little in common with the adult song. As the bird practices, the efforts begin to pay off. Examples that do not fit the memory are rejected; new ones are repeatedly tried until ones that start to fit are generated. These, in turn, are worked up until they are correct—that is, until they match well enough what is expected on the basis of what is represented. In other words, the template provides the target output and guides the continued practice, just as does the representation of some great recording that keeps a pianist practicing until he or she achieves a match with what he or she is listening to in his or her head.
Although the practice period in young white-crowned red sparrows is governed by a selective memory, one cannot conclude that these young birds know only the song of their parentage. Not only can these birds recognize exemplars of songs sung by other species, they can also learn songs that are outside the range of those produced by their species if such “novel” songs are the only ones heard during their sensitive period. Innate specifications contribute to song acquisition by biasing the selection processes during template formation and plastic song but not by usurping the need for learning.
Let me now restate my rational-constructivist approach to cognitive development (Feldman & Gelman, 1987). I share with Marler the view that some of what is innate is a set of guidelines that serve learners in the search for order in what would otherwise be a blooming, buzzing, confusion of sensory inputs. These are why some classes of inputs are salient given the particular learning goal. For example, innate skeletal structures in the domain of number direct early attention to collections of separate entities (in any modality). These underlie infants’ ability to match the numerosity of a visual display with the number of drum beats they hear on a given trial (Starkey, Spelke, & Gelman, 1990) and keep track of the surreptitious effects of addition and subtraction (Sophian & Adams, 1987). The fact that infants reliably discriminate between 2 and 3 items but not between 4 and 5 or 6 items does not rule out this conclusion, although many cite such results as strong evidence that they do (e.g., Strauss & Curtis, 1984; Fuson, 1988; Resnick & Greeno, in press). These conclusions are decidedly premature. To show why, I turn to Gallistel and Gelman’s (in press) model of nonverbal counting, in animals and infants.
In our model, we represent different cardinal numerosities with blurs of ordered magnitudes. These reflect the variability observed in numerosity discrimination studies with animals, which have been shown to discriminate numerosities for values of in the 50s. Because these blurs increase in width as a function of set size and start to overlap even for set sizes of 3 and 4, infants should have trouble discriminating between displays of 3 and 4 items. Animals frequently confound these two adjacent numerosities but nevertheless make systematic discriminations between much larger numerosities when the difference between the disciminanda is larger. Because there are no data on infants’ ability to discriminate between more widely separate large numerosities, infants’ ability to count preverbally has not really been tested. This is one reason we resist the conclusion that the infants’ ability to discriminate between arrays that vary in number is nothing but an ability to use the primitive sense data that underlie patterns of “twoness” and “threeness.” Another is that statements like the latter presume an implausible pattern perception model (Gelman & Gallistel, 1978, ch. 12), which may be why it has never been spelled out in a testable fashion.
To grant infants the ability to apply nonverbal counting and reasoning principles is not to say that they also know how to use the count words of their language as tags. This, children surely have to learn. They have to find, commit to memory, and practice at using the count words correctly. Available principles can direct children’s attention to inputs that have the potential to nurture the development in that domain. They also can serve as file drawers of memories and thereby keep together the kind of contents that, once understood, flesh out what were but skeletal structures at the start. But they cannot undo the need to learn in order to construct a full understanding. By limiting the innate knowledge base to skeletal principles, we make our position on this matter clear.
In sum, we grant very young learners principled cores of knowledge around which they can begin to assimilate and accommodate to relevant data An existing structure takes relevant data and keeps them together in memory so that they can become organized and coherent in their own right. This, in turn, sets the stage for an upgrading of what will be attended to and therefore nurture further development.
On the Nature of Relevant Input for Learning. Once we start using terms like structures and assuming that initial structures are skeletal in form, we commit ourselves to a constructivist account of acquisition, to the idea that learning is the construction of a model of the world, and that it is guided by model-building principles. Such an account allows that the model-building principles may use as inputs those data that are related in complex ways to the inductions drawn from them. Put differently, the requisite inputs are typically described in relational or structured ways; they are not presumed to have be low-level sensory bits and no longer need these bits be temporally and/or spatially paired. Given this, it is questionable that the empiricist law of frequency applies in a constructivist account of learning. First, if learners contribute to the interpretation and assimilation of what they experience, there is no guarantee that a given stimulus is interpreted the same way at different times. If the young do not share the exact same model for a given domain as do adults, they may not even treat a given datum as relevant, no matter how frequently it is offered. Second, it is not necessary that the exact same stimulus be presented repeatedly. Instead, it is important that one encounters multiple exemplars of inputs that share the same structural description. Indeed, the more opportunities children have with exemplars of the to-be-learned class of inputs, the greater are the chances of this happening in a timely way—that is, when they are able to recognize and use these as relevant input data. When inputs are omnipresent, the odds are more in favor of novice learners finding at least some exemplars of the class of relevant data and therefore converging on the to-be-learned abilities or concepts.
This leads me to propose that the Principles of Omnipresence and Redundancy, as opposed to a Principle of Frequency, support learning about structures. These principles do not function to foster the gradual build-up of habit strengths; they serve a maximizing function. It does not matter whether two examples of relevant data are the same in surface detail, whether these are produced by the same model, and so on. What matters is that they share the same structural characteristics. Where learning is grounded on innately given domain-specific outlines, novices can find relevant inputs for learning even when experts assume that none exist. This follows from the fact that available structures, no matter how skeletal in form, outline the kind of data needed for their further development. Because young learners actively deploy these structures, relevant exemplars will be found as long as they exist. Interestingly, some kinds of data are omnipresent.
The young are surrounded with samples of language, social interactions, objects that do or do not move on their own, tool use, and so on. Those who already are knowledgeable about such matters cannot help but generate relevant examples of these as long as they talk and interact—with social and nonsocial objects. Therefore, when children’s skeletal principles lead them to seek out nurturing data, the odds are extremely high that they will succeed, just as the sparrow is extremely likely to hear the songs it needs to hear. This is so even when we cannot characterize or even have the wrong ideas regarding the needed data. What matters is whether exemplars of the equivalence class are available at the right time from the child’s perspective. This is why those classes of data that are omnipresent, for example, speech samples, are the kind most likely to support the development of nascent structures.
Transcending the Initial Framework: The Case of Number
When conceptual development depends on mastering data whose structural characteristics are not readily mapped onto the characteristics demanded by the foundational model-building principles, learners nevertheless try to fit the data into the existing structure. This helps explain why opportunities to learn about fractions gives rise to misconceptions and confusions, but it makes even more mysterious the fact that a substantial proportion of school children eventually do learn that fractions are numbers. My speculations on how learning about fractions could begin are based on preliminary results from the latest in our series of studies on fractions.
This recent study introduced pretest experiences that my collaborators2 and I thought might be relevant to an understanding of fractions. Training experiences for kindergarten, Grade 1 and Grade 2 children were designed to try and illustrate that: One can generate a different number of equal units for a given whole; that this is so no matter what the kind and size of the whole; and that a given fractional term depends only on the relative size of a part to its whole. For example, children in the training conditions were shown whole circles and squares that came apart into equal halves, thirds, and fourths. In addition, they were encouraged to label the resulting unit and multiple-unit fractions with the correct noninteger numerlogs, for example, ⅓ and ⅔, respectively. Then, children were asked to rank order the training stimuli and tell us whether a given display was more than, less than, or equal to another display. We also had children learn to label displays that represented a whole number and a fraction, such as, 2½. Finally, introduction of the number line was more extensive than it had been in Gelman et al. (1989). When first shown a line in this study, children saw a short line with the numergraphs for 1 to 3 on it. Then they were shown the large line that would be used in the study and told that one could represent the numbers on the line with sets of N squares or circles instead of numerals. Then the experimenter encouraged the children to help her put the requisite number of circles needed to make this version of the number line look like it did from the start for children in the Gelman et al. (1989) study. (See Fig. 10.1.)
The study under discussion included a No-Control training condition where children received the exact same pretest trials as did those in Gelman et al. (1989). The training variable (No Training or Training) was crossed with a Labeling variable (No Label, Label) that was introduced during testing. Children in labeling conditions heard the appropriate numerical description for a given test display when they were asked to place it, for example, “Where does ⅔ go?” The remaining half of the children were in Non-Label Conditions and simply asked “Where does this go?” for parallel test displays.
During placement testing, children encountered five different kinds of items; unit fractions like ⅓; multiple unit fractions, like ⅔; mixed whole(s) and fractions, such as 1½ or 2⅔; regular wholes, for example, 3; and what we call mathematical wholes, for example, 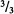 .
.
Figure 10.4 shows the success levels for kindergarten and Grade 1 children’s placements of the multiple-unit and mixed whole-and-fraction test displays. Although there is an effect of the training, it is not a straightforward one. To start our account triple interaction between Grade, Type of Display, and Labeling conditions, we turn to the kindergarten results.
Trained kindergarten children placed test displays more accurately if they did not hear the corresponding numerlogs for them at the same time. Indeed, offering the numerlog description of the displays depressed performance in all cells represented in Fig. 10.4 save one—that for the First Grade Label trials with mixed whole and fraction displays. Even these children did not consistently resist the interfering effects of the verbal input; they succumbed to the negative effects of hearing the nonunit numerlogs on the multiple-unit trials, that is when the depicted values was less than 1. Put differently, the pretest experience led these Trained Label children to be better at placing items between the numerical number line representations of 1, 2, and 3, than those between 0 and 1.
In summary, as might be expected, providing pretrained children with the verbal parallel to nonverbal representations of fractions did not help them succeed on our placement task. Indeed, talk about the numerical values typically depressed accuracy, especially in the kindergarten groups. By the first grade, the interference effect of offering the verbal description of an object-oriented representation of a quantity disappears for displays that depict values greater than 1; however, the interfering effect remains for test displays representing values of 1 > N and N < 0. These interfering effects are not restricted to the kinds of displays under discussion. Similar ones occurred with mathematical wholes, for instance, 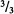 . To illustrate, kindergarten children who were trained and then tested without labels placed 43% of their Math Whole test displays correctly at 1. In contrast only 13% who were in the Label condition after training were correct. They had an overwhelming tendency to place items like
. To illustrate, kindergarten children who were trained and then tested without labels placed 43% of their Math Whole test displays correctly at 1. In contrast only 13% who were in the Label condition after training were correct. They had an overwhelming tendency to place items like 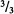 at 3.
at 3.
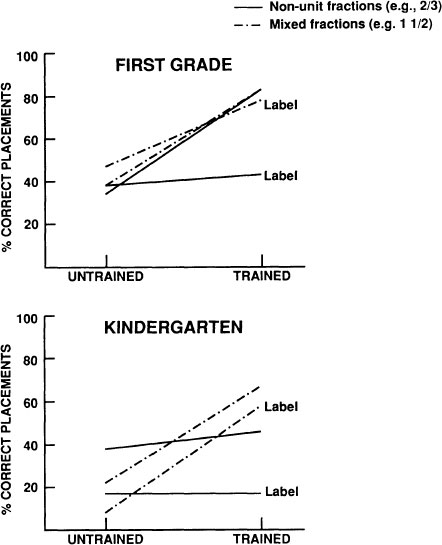
FIG. 10.4. Percent correct placements as a function of fraction test display type and condition for kindergarten and first grade.
These findings suggest that our pretraining experience helped the children in one way but not in another way. It did lead them to map the relative amount of one continuous quantity (area) to the relative amount of another continuous quantity, extent. This is why Trained children tended to do better than Non-Trained children. If the children had also learned to map numergraph representations of discrete quantity to continuous quantity, then there should have been a consistent positive, as opposed to a robust negative, effect of the labels. But it was not enough to teach the labels for different unit fractions to lead children to an understanding of how to map verbal representations of fractions to their number-line representations. Why?
Our answer is that, once again the children assimilated novel data to their underlying conviction that numbers are generated by counting things. The Grade 1 effects in the Trained Label group can be attributed to these children’s tendencies to treat their pretest labeling experiences as occasions to learn the “names” of new count words; to learn, for example, that one can use a count list that has entries between the whole numbers just like one can do this to keep track of birthdays. Because the names for entities of values of N < 1 have no meaning—the count words only start at 1 and westerners do not talk about being one-half-year old—these same children could not treat the names for the unit fractions in the same way. The result is that, whatever their understanding of these terms, it was kept separate from their understanding of counting and the corresponding count words, thereby setting the stage for them to make errors in interpreting the numerical language they heard whenever they were shown displays depicting values less than 1. These children’s common tendency to place displays with ⅔ of a circle where displays with 2 or 3 items belonged follows if we allow that they “heard” the label as “two” or “three” or even “two-three”, that is as novel instances of count words.
Putting together the Trained first grade children’s responses to the language of fractions, we conclude that their differential treatment of fraction labels for values of N > 1 versus values of N < 1 means that these children have yet to modify their idea of what are or are not numbers. Instead, they have begun to modify their idea of what is an acceptable counting list, a list that still starts at 1 but now might go “one, one-and-a-half, two, two-and-a-half, and so on.” Support for this conclusion is found in these same children’s answers to our questions of whether there are numbers between the number pairs (1, 2) and (0, 1).
In this part of the interview, children were asked whether there are numbers between 1 and 2 and if they denied there were, they were then probed, “How about 1½?” After this, they were asked whether there are numbers between 0 and 1. Once probed, 90% of the Grade 1 children allowed that there are numbers between 1 and 2. Nevertheless, they did not transfer what they had just acknowledged. When immediately asked the question about 0 and 1, 66% denied there were numbers between these; even when they were probed, 50% continued to say there were no numbers between 0 and 1. Explanations like, “You can count one, one-and-half, two, two-and-half, but you can’t count zero, zero-and-a- half” indicate that children meant what they were saying. They also make it clear that the children are still far from a true understanding of fractions, let alone that the number line is pseudodense. Still, it would be wrong to say that they did not make real progress.
The fact that children now talk of numbers that are between “one” and “two” is significant, even if they do not understand that they are talking about fractions. For whatever their understanding, the talk is consistent with the induction that even more “numbers” could come between each of those in the extended list. Learning like this could support the induction of the principle of pseudodenseness and an appreciation as a consequence, that some of the original principles of counting loose their general validity, such as the principle that there is a next number. In other words, although the children still have much to learn, they have managed to learn the kind of thing that leads onto a learning path that could take them through the kinds of inductions that will contribute to a new understanding of number.
Lest the reader conclude that it is easy to structure environments to accomplish the preceding, we confess that we did not know in advance whether the children would accept any of our offerings. The fact remains, children bring their own interpretations to the inputs we provide them and they need not see things as we want them to.
This hypothetical course of conceptual development just discussed is interesting from the standpoint of Carey’s (this volume) discussion of commensurate and incommensurate concepts. The natural numbers in the system of rational numbers nave a meaning that is commensurate with their meaning in the system that consists only of the natural numbers. Two is still the next natural number after one, the natural numbers are ordered, their addition and subtraction yields the same results, and so on. The same can be said of the extended count sequence corresponding to 1, 1½, 2, 2½, and so on. On the other hand, the term number itself has incommensurate meanings in the two systems, as shown by the fact that some phrases involving this term have meaning or make reference in the original system, but have no meaning in the rational number system. There is no referent for the phrase, “the next number after one half.” There is, strictly speaking, also no referent for the phrase, “the next number after one,” although in almost any context both questioner and questioned would understand that this phrase was really meant to be “the next natural number after one.” This, by the way, illustrates the inherently complex and context-dependent nature of verbal meaning, which is part of what makes it hard for children to learn to deal with the verbal instantiation of the system of arithmetic reasoning.
A FINAL WORD
When learners do not have existing structures to guide their search for and correct interpretation of nurturing inputs, they no longer can be counted on to find their own food for thought. Left to their own devices, pupils have every reason to continue in a direction that will yield misconceptions. It would seem that experts do have to help novices package the environment—indeed, there is a premium on their being able to do so. Assuming that we can specify and organize inputs, we still cannot count on matters going as we want. The constructivist mind of the child can always veer in another direction if it does not yet share with us the same structures of knowledge. We have to be prepared to probe their understandings and make special efforts to draw children’s attention to relevant characteristics of the data. Under the circumstances, it would seem wise to unleash the entire armament of whatever tools we have for providing the necessary kind of structured data base. It is for these reasons that I agree with those who suggest that the conceptual change is more likely to occur when the input conditions resemble a language-cum-concept immersion program. I think pupils are more likely to encounter structured data, to practice at using what they are learning, and to come to understand how to interpret the terms and symbols of the domain if given a fair chance to become fluent in using both the structure and the language of the domain. When put this way, it should be clear why I think that the languages of science and mathematics are better thought of as different languages than the one we use in everyday talk (Gelman, Massey, & McManus, in press).
ACKNOWLEDGMENTS
The research reported here, as well as the preparation of the chapter, were supported by National Science Foundation (NSF) grants BNS 85–19575 and BNS 89–16220, as well as a University of California at Los Angeles (UCLA) Dean’s Fund. I am grateful to the team of researchers who helped on the data collection and coding of the fraction placement studies, the children and their parents, the teacher and school administrators who agreed to participate in the research, and the members of the Cognitive Development Lab at the University of California at Los Angeles (UCLA) who worked on every aspect of the preparation of this manuscript. Special thanks are due to C. R. Gallistel, who served as my sounding board as I tried to talk about the clues I thought the data offered, Melissa Cohen, Patrice Hartnett, Jason Macario, Chris Massey, Elizabeth Meck, and an anonymous mathematics curriculum expert, all of whom were centrally involved in the conception of the various studies reported here.
REFERENCES
Behr, M. J., Wachsmuth, I., Post, T. R., & Lesh, R. (1984). Order and equivalence: A clinical teaching experiment. Journal for Research in Mathematics Education, 15(5), 323–341.
Carpenter, T. P., Corbitt, M. K., Kepner, H. J., Lindquist, M. M., & Reys, R. E. (1981). Decimals: Results and implications from the second NAEP mathematics assessment. Arithmetic Teacher, 28(8), 34–37.
Carraher, T. N., Carraher, D. W., & Schliemann, A. D. (1985). Mathematics in the street and in school. British Journal of Developmental Psychology, 3, 21–29.
Chomsky, N. (1957). Syntactic structures. The Hague: Mouton.
Cohen, M., Gelman, R., & Massey, C. (in preparation). Young school-aged children interpret written fractions as novel count numbers. Department of Psychology, UCLA, Los Angeles, CA.
Feldman, H., & Gelman, R. (1987). Otitis media and cognitive development. In J. F. Kavanagh (Ed.), Otitis media and child developement (pp. 27–41). Parkton, MD: York Press.
Fuson, K. C. (1988). Children’s counting and concepts of number. New York: Springer-Verlag.
Gallistel, C. R. (1990). The organization of learning. Cambridge, MA: MIT Press.
Gallistel, C. R., & Gelman, R. (in press). Subitizing: Subvocal rapid counting. In W. Kessen, Ortony, F., & Craig, Fr. (Eds.), Essays in honor of George Mardler. Hillsdale, NJ: Lawrence Erlbaum Associates.
Gelman, R. (1990a). First principles organize attention to and learning about relevant data: Number and the animate-inanimate distinction as examples. Cognitive Science, 14, 79–106.
Gelman, R. (1990b). Structural constraints on cognitive development: Introduction to a special issue of Cognitive Science. Cognitive Science, 14, 3–9.
Gelman, R., & Cohen, M. (1988). Qualitative differences in the way Down’s Syndrome and normal children solve a novel counting problem. In L. Nadel (Ed.), The psychobiology of Down’s syndrome (pp. 51–99). Cambridge, MA: MIT Press.
Gelman. R., Cohen, M., & Hartnett, P. (1989). To know mathematics is to go beyond thinking that “fractions aren’t numbers.” Proceedings of the Eleventh Annual Meeting of the North American Chapter, International Group for Psychology of Mathematics Education. New Brunswick, NJ.
Gelman, R., & Gallistel, C. R. (1978). The child’s understanding of number. Cambridge, MA: Harvard University Press.
Gelman, R., Massey, C. M., & McManus, M. (in press). Characterizing supporting environments for cognitive development: Lessons from children in a museum. In J. M. Levine, & L. B. Resnick (Eds.), Perspectives on socially shared cognition. Washington, DC: American Psychological Association.
Gelman, R., & Meck, E. (in press). Early principles aid early but not later conceptions of number. In J. Bideaud & C. Meljac (Eds.), Les chemins du nombre. Paris: Les Presses Universitaires De Lille.
Gleitman, L. (1990). The structural source of verb meanings. Language Acquisition, 1, 3–55.
Gottlieb, G. (1983). The psychobiological approach to developmental issues. In M. M. Haith & J. J. Campos (Eds.), Infancy and developmental psychobiology (Vol. 2, pp. 1–26). New York: John Wiley and Sons.
Hiebert, J., & Wearne, D. (1986). Procedures over concepts: The acquisition of decimal number knowledge. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 197–223). Hillsdale, NJ: Lawrence Erlbaum Associates.
Invitation to mathematics. (1988). Glenview, IL: Scott, Foresman.
Kerslake, D. (1986). Fractions: Children’s strategies and errors. A report of the strategies and errors in the secondary mathematics project. Windson, England: Nfer-Nelson.
Landau, B. A., & Gleitman, L. (1985). Language and experience: Evidence from the blind child. Cambridge: Harvard University Press.
Lave, J. (1988). Cognition in practice: Mind, mathematics and culture in everyday life. New York: Cambridge University Press.
Naigles, L. G., Gleitman, L., & Gleitman, H. (in press). Children acquire word meaning components from syntactic evidence. Journal of Child Language.
Nesher, P., & Peled, I. (1986). Shift in reasoning. Educational studies in mathematics, 17, 67–79.
Pinker, S. (1989). Learnability and cognition: The acquisition of argument structure. Cambridge, MA: MIT Press.
Resnick, L. (1988). Learning in school and out. Educational Researcher, 16, 13–20.
Resnick, L. B., & Greeno, J. (in press). A theory of the intuitive origins of mathematics. In J. Campbell (Ed.), The nature and origins of mathematical skills. Elsevier Science: Amsterdam.
Saxe, G. B., Guberman, S. R., & Gearhart, M. (1987) Social processes in early development. Monographs of the Society for the Research in Child Development, 52 (Serial No. 216).
Saxe, G. B., & Posner, J. K. (1983). The development of numerical cognition: Cross-cultural perspectives. In H. P. Ginsburg (Ed.), The development of mathematical thinking (pp. 291–317). New York: Academic Press.
Sophian, C., & Adams, N. (1987). Infants’ understanding of numerical transformations. British Journal of Developmental Psychology, 5, 257–264.
Starkey, P., & Gelman, R. (1982). The development of addition and subtraction abilities prior to formal schooling in arithematic. In T. P. Carpenter, J. M. Moser, & T. A. Romberg (Eds.), Addition and subtraction: A cognitive perspective (pp. 99–115). Hillsdale, NJ: Lawrence Erlbaum.
Starkey, P., Spelke, E. S., & Gelman, R. (1990). Numerical abstraction by human infants. Cognition, 36, 97–127.
Strauss, M. S., & Curtis, L. E. (1984). Development of numerical concepts in infancy. In C. Sophian (Ed..), Origins of cognitive skills (pp. 131–155). Hillsdale, NJ: Lawrence Erlbaum Associates.
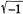 ” as a number, a single entity to be added, subtracted, multiplied, and divided just like “1” and “2.” Second, one has to come to terms with the fact that the fractions make the system of number pseudodense. The numbers no longer lie at separated intervals along the number line. One does not move by steps of significant magnitude from one number to the next; rather, the next number in the sequence lies infinitesimally close to its predecessor. Put another way, one cannot say what the distance is between one rational number and the “next” rational number, because there is no such thing as the “next” rational number. This is a structural feature of the “rational” number system that is not present in the “natural” number system, which is the only available structure to which the child can assimilate these weird beasts. Finally, there is no simple, counting-based verbal algorithm for comparing, adding, and subtracting these multipart symbols for the nonexistent “numerosities” that lie between one and two, three and four, and so on.
” as a number, a single entity to be added, subtracted, multiplied, and divided just like “1” and “2.” Second, one has to come to terms with the fact that the fractions make the system of number pseudodense. The numbers no longer lie at separated intervals along the number line. One does not move by steps of significant magnitude from one number to the next; rather, the next number in the sequence lies infinitesimally close to its predecessor. Put another way, one cannot say what the distance is between one rational number and the “next” rational number, because there is no such thing as the “next” rational number. This is a structural feature of the “rational” number system that is not present in the “natural” number system, which is the only available structure to which the child can assimilate these weird beasts. Finally, there is no simple, counting-based verbal algorithm for comparing, adding, and subtracting these multipart symbols for the nonexistent “numerosities” that lie between one and two, three and four, and so on.
 over
over  . This pattern of results for the second graders suggests that they memorized some things about ½ and ¼, but still had little understanding of these as fractions. This conjecture gains support when we consider how these children answered when asked whether there were numbers between 1 and 2 and between 0 and 1. Five of the 12 children allowed that there was one number between 1 and 2; only three were as generous when they considered whether there are numbers between 0 and 1. Our next study provides more evidence that second graders have a way to go to achieve an understanding of the relevant symbol system.
. This pattern of results for the second graders suggests that they memorized some things about ½ and ¼, but still had little understanding of these as fractions. This conjecture gains support when we consider how these children answered when asked whether there were numbers between 1 and 2 and between 0 and 1. Five of the 12 children allowed that there was one number between 1 and 2; only three were as generous when they considered whether there are numbers between 0 and 1. Our next study provides more evidence that second graders have a way to go to achieve an understanding of the relevant symbol system.
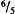 , was more; that is, only 47 and 27 percent correctly chose ½ and
, was more; that is, only 47 and 27 percent correctly chose ½ and 
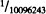 and 3.276542169, as opposed to the obvious answers of 3½ or 3.5. This contrasts with the 10% and 5% of the pupils in the regular Grades 7 and 8 classes who wrote something other than 3½ or 3.5. To our surprise, there even were students in these later grades (5% and 17%, respectively) who either denied that there were any numbers between 3 and 4, wrote a whole number like 2, or skipped the item.
and 3.276542169, as opposed to the obvious answers of 3½ or 3.5. This contrasts with the 10% and 5% of the pupils in the regular Grades 7 and 8 classes who wrote something other than 3½ or 3.5. To our surprise, there even were students in these later grades (5% and 17%, respectively) who either denied that there were any numbers between 3 and 4, wrote a whole number like 2, or skipped the item.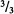 .
.