Egyptian society was concurrent with a number of great Mesopotamian empires; however, those empires rarely lasted more than a couple of generations, being brought down by barbarians or a warlord with a desire for an empire of his own. Although it was a great civilization, Mesopotamia suffered from constant turmoil and abrupt change. Although equally as large, Egypt was more of a nation than an empire. For almost three thousand years, Egypt remained relatively stable. There were a few “intermediate” periods consisting of either internal strife or foreign influence, but these were small compared to the thousands of years of internal peace.
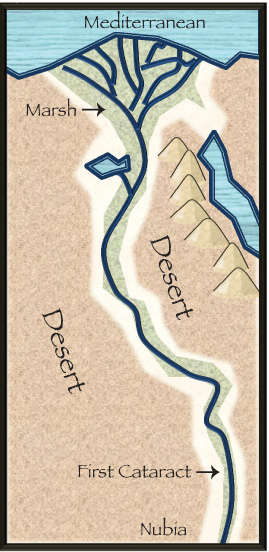
Egypt owed much of its stability to its unique geography. The land simply kept the violent outsiders away. In order to understand ancient Egypt, however, we must realize that modern borders meant little in the ancient world. Egypt was split into two parts: the Nile valley and the northern delta. The valley is hundreds of miles long but never more than about ten miles wide. A map of this part of Egypt would look like a long string winding its way through the desert. The western desert comprised the harsh sands of the Sahara Desert. The eastern desert was a stony, mountainous landscape. Neither side could support enough people to seriously threaten the Egyptians who lived on the banks of the Nile, and both sides presented a sweltering, waterless barrier to outside invaders.
The Egyptians were also relatively protected in the south. Most nations have trouble defending borders that span up to a thousand miles long. In order to protect the entire country, they would need to disperse their armies into small, vulnerable groups. The southern border of Egypt was only a few miles wide because it consisted only of the width of the Nile and its banks. It was easy to concentrate troops at this one point. Egyptians had little fear of an armada sailing downriver from the south. The Nile has a series of rapids, called cataracts, along its southern portion. Large boats could not navigate these waters and would have to be portaged over land to get around them. The Egyptians wisely built forts at these points to harass any fleet that attempted this tactic.

Ancient Egypt.
The northern delta was also fairly safe. This triangular region was also protected on the east and west by desert. The delta did have some vulnerability due to its long border with the Mediterranean, but this was not as bad as it might seem. During most of Egypt’s history, sea travel was a risky business. Ship-building technology had not progressed far enough at this time. Any king would be taking a great risk by placing the army charged with protecting his kingdom in a series of not-so-seaworthy ships. One storm could wipe out the bulk of his armed forces.
Even if an invading force managed to sail a fleet to the delta, it would immediately encounter problems. Ships that can survive in the sea are not very good on rivers and would be at a serious disadvantage against Egypt’s river fleet. If the force attempted to disembark and proceed on foot, they would run into other problems. The delta consists of many small islands surrounded by the branches of the Nile. This area is swampy and not conducive to moving heavy military equipment. If an invading army conquered one of the islands, they would have to load all of their equipment back in their boats and sail to another. Holding an island would force them to leave men behind, splitting their troops. In any case, the time such operations took would enable the Egyptians to mount a large-scale response. Clearly, Egypt was safe until seafaring and military technology advanced to the point of overcoming these obstacles.
According to one of the Egyptian theologies, Ptah formed the world out of chaos, which still surrounded it. Egypt was the center of this world, and as you moved away from Egypt, the closer you came to this disorder. The violent and barbaric ways of the outsiders probably seemed natural to the Egyptians’ world view because the foreigners bordered the primal chaos. Egyptians had little respect for and wanted little to do with non-Egyptians. In many ways, this view was justified despite its seemingly racist overtones. Imagine how a pharaoh whose position was based on a thousand-year-old tradition would view a Mesopotamian king who recently secured his position through violence and plunder. Egypt had little contact with the outside world and had little desire to change that situation. As a result, Egypt developed in its own way and did things radically differently from the rest of the world. This is not to say that there was no foreign influence on the Egyptians, but they had the ability to reject or accept ideas as they saw fit, and they were predisposed to reject them. Nowhere is this more apparent than in the way they dealt with fractional values.
The Mesopotamians had a system remarkably close to our decimal system except that they used base sixty. When we want to express a half, we write 0.5 in decimal form because 5 is half of 10. When the Mesopotamians wanted to write one-half, they wrote something like 0.30, since 30 is half of 60. Actually, they didn’t have zeros or a “point” symbol, so they would just write a symbol that represented 30. In any case, this is why today half an hour is 30 minutes. We’re still writing the “decimal” value of time in ancient Mesopotamian. We essentially use the Mesopotamian system today in part because they were not isolated from the rest of the world of which we are a part.
The Egyptian method seems decidedly strange to the modern mind. They only used parts, like a fourth or a tenth. The hieroglyphic representation of a fourth was simply the number four under the symbol of a mouth. The mouth symbol makes an r sound in the Egyptian language. It’s possible that they added er to the end of a number, just as we add th to the end of a number like ten to form a part, like a tenth.

One-fourth written in hieroglyphs.
So a fifth could be written OAAAAA and a thirteenth as OSAAA. We will use the modern shorthand of placing a bar over the number, so f will be used to represent an Egyptian fourth. Today these numbers are called unit fractions. A fourth is the fraction ¼. The word “unit” refers to the 1 in the numerator of the fraction. This is a misnomer because Egyptian fractions are not fractions in the modern sense. There is no 1 in the numerator because there is no numerator.
When modern mathematicians are confronted with Egyptian fractions, they often shake their heads in dis-belief. Remember that Egyptian notation could express fractions only where we would put a 1 in the numerator. There simply was no way to write 2/5. When Egyptians wanted to express this value, they had to write d ag. This is 2/5, since ⅓ + 1/15 is 2/5. Who would possibly want to express non-integer values as the sum of fractions? The answer is simple. We would, and we do it every day.
Every math student eventually learns the approximation 3.14 for π. What does the representation 3.14 mean? If you’re sufficiently familiar with the base system, you should recognize that this is the sum of three parts: a unit, a tenths, and a hundredths part. So when we write 3.14 we really mean this:
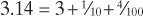
But this can be simplified to the following:
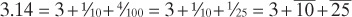
Just as we ignore the plus signs between the parts of our decimal representations, so did the ancient Egyptians. They might represent the quantity 3.14 as 3 a; sg or in hieroglyphs as AAA IS PSSAAAAA. I think part of the problem modern mathematicians have in appreciating Egyptian mathematics is the phrase we use to describe their numbers, “unit fractions.” We compare their system to our system of fractions instead of to our decimal system, with which it has far more in common.
To truly comprehend the Egyptian system of fractions, we must deeply understand the properties of our decimal system that make it so effective. Imagine that you won the lottery. Someone calls you up on the phone and tells you that you won 28 million and.… At this point your phone drops the signal. The caller was going to say $28,732,593, but they only got off two of the eight digits. Yet only hearing 28 million, you have a very good approximation of what you’ve won. Technically, the number is the sum

The sum of the last six terms is dwarfed by the first two numbers, so we don’t really need to add all the terms to get a good idea of the total value.
The same holds true for decimals. Consider the following approximation for the square root of two, 1.414214. To an untrained eye, this expression is overly complicated. It’s the sum of an integer and six different fractions, each with a different denominator. It consists of parts measured in millionths, parts too small to intuitively grasp. Yet when we look at it, we immediately see a number close to one and a half, or a little more than 1.4. The beauty of the decimal system is that it gives as little or as much information as you need. I can view the representation of the approximation of the root as a little more than 1.4 or a little more than 1.41 or a little more than 1.414. With each phrase I’m forced to tolerate more complexity in exchange for more accuracy. The best part is that the choice is ours. The rapidly declining significance of the place values gives us power to adjust our number interpretations to our needs. It gives us a quick approximation together with an accurate estimation.
The Egyptian system does exactly the same thing. Their representation of 3.141, 3 a; sg a;;;, can be quickly assessed as a little more than 3 1/10. If they need more accuracy, they can include more “digits.” For contrast, let’s compare this system to our fractional system. Try to guess the rough value of 4586/1310. Can you come up with an estimate? Even if you can, do you have any idea how close your approximation is? However, in Egyptian this number is 3 s ada;, which is obviously a number less than a thousandth away from 3 ½. Clearly the Egyptian system has more in common with our place-value system. Just like our decimal system, there’s an easy balance between accuracy and estimation.
One common observation of the Egyptian system of fractions is that they never would write the same fraction twice within one number. So you never see a number like 7 g g. This so-called rule is more likely the misinterpretation of a more general rule of thumb. Think of our decimal representation of this number:
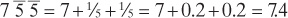
Our placement system refuses to accept repeated digits, which is perhaps the reason we take this for granted. If we tried to force 7 g g into our decimal system we might get something like this: 7.2.2. We would then interpret this as a number close to 7.2, but it isn’t. It’s actually 7.4, and 7.2 is a bad approximation. Similarly the Egyptians would not tolerate g g. It’s not close to a fifth. It’s twice as big as a fifth. To be off by 100% in an approximation is terrible. The Egyptians would write this fraction as d ag. The fraction is close to a third, not a fifth. It’s a third and a little bit more. It’s important that ag is significantly smaller than d because it is a refinement of an approximation. So they know it’s basically a third, and if they need more accuracy, they can add the fifteenth.
The rule applies to more than just equal fractions. The Egyptians would never write g h, since a sixth is too close to a fifth to be a refinement. This number is not close to a fifth—it is almost twice as much. So they would instead write d d;. We can easily check to see that these represent the same value as follows:
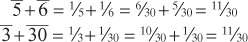
As a result, Egyptian fractions are fairly easy to read. But isn’t it difficult to work with fractions that have radically different denominators? We will see that it is true only if you stick to the modern method, but not if you calculate like an ancient Egyptian.
One of the most common duties of an ancient Egyptian scribe was to pay the workers. This was not always easy because they often received shares for pay and not a set salary. A scribe would receive some amount of food and have to divvy it out fairly according to each worker’s share value. Not every job had equal shares, just as today not every job has an equal salary. For the purpose of this section, however, we’ll assume everyone has a share value of 1.
Assume that seven workers get a loaf of bread to share. This isn’t very realistic because they were usually paid in grain, but let’s accept it for argument’s sake. The scribe realizes that one loaf divided between seven men means that each gets a seventh, which the scribe would record as j in his records.

One loaf of bread cut up to feed seven workers.
So far everything is working out well. However, the next day the workers get four loaves of bread. The scribe could cut each loaf of bread into seven pieces and give each worker four, but it seems like too much cutting and the workers won’t appreciate all the small pieces. The scribe gets an idea and decides to cut each loaf in half. Now he has eight pieces, enough to give each worker one and he has one left over.

The loaves cut in half make one piece for each of the seven workers with one left over.
Being an honest scribe, he doesn’t keep the one remaining piece for himself but cuts it into seven pieces, one for each worker. The size of the smaller pieces is a seventh of a half, which is a fourteenth, since 7 × 2 is 14.

When the eighth piece is cut into seven, the smaller pieces can be handed out to the workers.
So each worker gets a half loaf and a fourteenth of a loaf, which the scribe records as s af.
Note that we’ve just performed our first Egyptian division involving fractions. We now know that 4 ÷ 7 = s af. Although this was not their typical method of division, it does show how natural the Egyptian system is. It’s also possible that their method of fractions was formed from similar considerations.
Let’s try another division.
EXAMPLE: Divide 3 by 16 using “sliced bread.”
Before we can begin, we need at least 16 slices so each worker can get one. If we were to cut each loaf into four pieces, we would get only 12 slices. Mathematically, this tells us that 3 ÷ 16 is smaller than f, so we can’t write the division as f plus some other fractions. If we cut each loaf into 6 slices, we get 18 slices, which is more than enough for the 16 workers. We’ll perform the first slice and mark off the 16 slices that will be distributed.

Three loaves to be divided between 16 workers. After cutting them in sixths, each worker gets one, leaving two slices.
We now know that each worker gets h of a loaf with 2 slices left over. If the scribe now cuts the remaining 2 slices into eight pieces, he gets 16 smaller slices, which is one for each worker. The size of these smaller slices is fk since we cut an eighth of a sixth and 8 × 6 is 48. This makes 3/16 equal to h fk. The final answer is as follows:
SOLUTION: h fk

The remaining two slices get cut into eighths and distributed to the 16 workers.
PRACTICE: Divide 2 by 5 using “sliced bread.” Make your first cuts as thirds.
ANSWER: d ag
PRACTICE: Divide 4 by 18 using “sliced bread.” Make your first cuts as fifths.
ANSWER: g fg
Note that some divisions can’t be done in two slices. Consider the following problem:
EXAMPLE: Divide 4 by 5 using “sliced bread.”

Four loaves cut in half with each of five workers getting one slice. Three halves are left over.
If we cut the loaves in two, we’ll get eight slices. We hand out five of them to each of the five workers, leaving three halves.
We can treat these three remaining halves just as we would three whole loaves. In order to divide three “loaves” into five, we can cut each in half. Note that these are already halves so half of a half is a fourth. Now the three halves become six pieces of size f, of which we can give one to each worker leaving one of the fourths.

The three remaining halves can be cut in half. Five of the six pieces are distributed between the workers.
We can now cut the remaining fourth into five pieces, giving each worker a piece of size s;. This makes 4/5 equal to s f s;.

The remaining quarter is cut in five pieces and given to the workers.
ANSWER 1: s f s;
The above example shows us that divisions might require three or more fractions in the solution. This should not come as a surprise since Egyptian fractions are closer to our decimals than to our fractions. You should realize that just as decimals may require a lot of digits, like 8.77928347723, so Egyptian math may require many fractions.
Note that in the above problem we did not need to cut all of the original four pieces in half. By cutting the first three pieces in half we would get six halves, enough to give one to each of the five workers.

This time only three of the loaves are cut in half.
We can now cut both the half and the remaining whole into five pieces each. So now each worker gets a half, a fifth of a half, and a fifth, or equivalently s a; g.

The half and the whole loaf are each cut into fifths.
Each worker gets two slices, one small and one large.
ANSWER 2: s g a;
Note that we got two different answers for the same problem. This means that Egyptian fractions can be written in more than one way. Specifically we see for the above problem that f s; is the same as g a;.
PRACTICE: Divide 5 by 7 in two ways using “sliced bread.”
ANSWER: s h sf ahk or s j af
You might argue that having more than one way to write a number is extremely awkward, but as I mentioned in the introduction, we see difficulties in alien systems far more easily than we notice them in our own. In our number system all of the following are exactly the same.
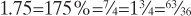
At least the Egyptian system is consistent with the way it portrays numbers even though they are not exactly the same.
Once each year the star Sirius would disappear behind the sun. Toward the end of this period, the Egyptians would scan the skies at dawn, searching for its return. The first day of its reappearance marked the beginning of a new year. This sign from the gods foretold the coming of the inundation—soon the Nile would flood, ending the harvest season. All of Egypt would then be covered by water except for the settlements on the banks and the higher islands of the delta. There wasn’t much for the Egyptians to do except wait for the flood to recede, and yet this was the most crucial time in the Egyptian year.
The flood carried with it the two most valuable resources in Egypt, water and topsoil. Obviously water is as good as gold in a land surrounded by desert. The Egyptians built barriers to trap the flood waters and use them for irrigation in the drier seasons. Water was so precious that restricting its flow onto your neighbor’s farm was an offense punishable by damnation during your soul’s final judgment in the Hall of Osiris.
The flood waters also brought the most fertile topsoil found in the Mediterranean. During its four-thousand-mile journey, the waters of the Nile picked up nutrients and then scattered them throughout Egypt, enabling a huge civilization to flourish in the desert. The color of this rich soil lent the very name used by the Egyptians to describe their home, the Black Land.
The size of the flood varied from year to year. Some farmland was replenished annually. Other areas received the life-bringing waters only in high-flood years. The scribes of Egypt assessed the value of farmland based on how likely it was to be inundated. Too many years of low waters could result in famine for a culture that was overly dependent on the bounty of the Nile. However, if the flood was too high, their homes on the banks would have been threatened. The Egyptians needed to know the extent of a year’s flood, so they invented the nilometer. This measuring device is essentially a stone stairway that descended to the Nile. As the waters rose, individual stairs would be covered in water, and marks on the nilometer would give the depth of the water. Hence the nilometer was essentially a giant ruler built into the Nile.
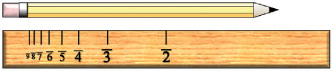
Reading a ruler tells us a lot about the way decimals are used to make approximations. Consider measuring a pencil with a ruler. In the diagram below, the ruler shows us that the pencil is somewhere between 8 and 9 inches. If we approximate the length as 8 inches, we’ll be off by at most 1 inch.
If we want more accuracy, we could look at the smaller ruler marks indicating tenths of an inch between 8 and 9. Below we can see that the tip of the pencil falls between the sixth and seventh tick mark between 8 and 9. So the pencil length is between 8.6 and 8.7 inches. If we approximate the pencil length as 8.6, we will be off by at most 0.1 inches.

The length is estimated by the marks the point falls between.
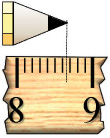
The pencil is between 8.6 and 8.7 inches.
There are a couple of things we should note. The first is that the distance between the ruler’s marks determines the accuracy of the measurement. In fact, this distance is exactly the maximum error. The latter can be calculated by subtraction. The above pencil point falls between the 8.6 and 8.7 mark, and hence the maximum error is 8.7 – 8.6 = 0.1. We should also note that in a decimal measurement system, the distance between marks is uniform. This makes the error the same no matter where on the ruler our measurement occurs. This is not true for Egyptian fractions.
If we made a ruler marked with Egyptian fractions, it would look like the following diagram. In the middle would be the mark for s since it’s half way. Similarly, one-third of the way over, we would find d, and so on. The marks would become more tightly packed for the smaller measurements. They get so close that eventually we would have to stop marking the ruler so they didn’t overlap.
The pencil being measured below is 3/16 of a foot long. The ruler shows it being longer than a sixth of a foot but less than a fifth. If we convert 3/16 into Egyptian fractions, we get h fk. The Egyptian number verifies that it is a little, specifically a forty-eighth, more than a sixth.

The marks are close below s, and hence the measurement is more accurate.
Someone measuring the pencil with the Egyptian ruler can tell that it’s more than a sixth but can’t exactly tell by how much. Since the marks are not uniformly distributed, it’s not as easy to know the largest possible error as it would be with a more conventional ruler. However, we can calculate the error by finding the distance between the h and g marks using subtraction. Since I haven’t taught you yet how Egyptians subtract fractions, we’ll use modern methods.
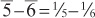
The common denominator is 30 and we can get both to be 30 by multiplying the 1/5 by 6 and the 1/6 by 5 giving
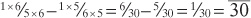
Note that the error of a measurement between g and h is d; and 30 is 5 × 6. It’s not difficult to show using algebra that this is always true provided the Egyptian fractions are adjacent numbers. Hence the error measurement between a; and aa would be at most aa;. A mathematician would phrase this as “the error of an Egyptian fraction is roughly the square of the smallest term.”
We actually didn’t even need to subtract the two values; we could just have easily noticed that the two lines on the ruler are “really close.” They’re all really close on the left side of the ruler, and hence all measurement on this half would be fairly accurate. However, there seems to be a problem with the right side. The following pencil is 5/6 of a foot long. The best our ruler can do now is to estimate it as more than s. In fact we can write 5/6 as s d in Egyptian fractions. Unfortunately, a half is a bad approximation for 5/6. If we treat the s as the approximation and the d as the error term, the error is 66 ⅔% of the estimate, which is too big to be considered accurate.
Objects that extend into the right half of the ruler are subject to bad approximations. The error is the distance from the s to the pencil tip.
This seems to fly in the face of our interpretation of Egyptian fractions as being a system of arbitrarily good approximations. However, the Egyptians solved this problem, and they did it in the most obvious way. Thinking in terms of rulers, the difficulty arises because there are no marks on the right-hand side of the ruler. So the Egyptians included an extra a mark or two.

The hieroglyphic 2/3.
By far, the more common of the two fractions added to their “ruler” is ⅔, symbolized by the following hieroglyph. We will use the modern transcription, ', for this symbol.
The choice of symbol is truly inspired. It looks like the mouth and is used to denote a fraction over the number 1 and “a half.” This is in fact what ⅔ is. In modern terms we get
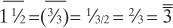
We’ll look at this relation in more detail later. Right now let’s see the impact it has on approximations in measurement. Here’s our previous pencil measurement using a ruler with the ' mark added.
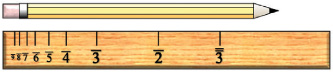
The distance between the ' mark and the pencil tip is smaller than that of the s mark. Hence the error in measurement is reduced.
Now the ruler reads ⅔ and a little more, and the ⅔ is a much better approximation than the ½ we had previously. The Egyptians would express the length of the pencil as ' h rather than s d. If we treat the length as roughly ' with an error of h, we get a 25% error, which is much better than the 66 ⅔% error we got with s d.
You might argue that the gap on the ruler to the right of the ' is still a bit large. If you do, you’ll find that a fairly small group of ancient Egyptians agree with you. It’s extremely rare, but there are instances of a special symbol for ¾ being used. Most Egyptians seem to have felt that the ⅔ symbol was sufficient, and we will restrict ourselves to ', since the mathematical rules involving it are clearly spelled out by ancient texts.
When I first learned of the ' symbol, I was uncomfortable. Mathematicians like consistency and order. This symbol, being unique, bucked the rules and had to be treated with special operations. However, as I became more proficient with Egyptian mathematics, I began to understand that this gave their mathematical system added flexibility. In order to begin to appreciate the versatility of Egyptian math, we’ll need to learn its basic operations.