Accelerated Optimization for Machine Learning

Appendix A

Mathematical Preliminaries

In this appendix, we list the conventions of notations and some basic definitions and facts that are used in the book.

A.1 Notations

Notations	Meanings
Normal font, e.g.,s	A scalar
Bold lowercase, e.g.,v	A vector
Bold capital, e.g.,M	A matrix
Calligraphic capital,	A subspace, an operator, or a set
e.g., $\mathbb {T}$
$\mathbb {R}$ , $\mathbb {R}^+$	Set of real numbers, set of nonnegative real numbers
$\mathbb {Z}^+$	Set of nonnegative intergers
[n ]	{1, 2, ⋯ ,n }
$\mathbb {E} X$	Expectation of random variable (or random vector)X
I ,0 ,1	The identity matrix, all-zero matrix or vector,
	and all-one vector
x ≥y	x −y is a nonnegative vector
X ≽Y	X −Y is a positive semi-definite matrix
f (N ) = O (g (N ))	∃a > 0, such that $\frac {f(N)}{g(N)}\leq a$ for all $N\in \mathbb {Z}^+$
$f(N)=\tilde {O}(g(N))$	∃a > 0, such that $\frac {\tilde {f}(N)}{g(N)}\leq a$ for all $N\in \mathbb {Z}^+$ ,
	where $\tilde {f}(N)$ is the function ignoring poly-logarithmic
	factors inf (N )
f (N ) = Ω(g (N ))	∃a > 0, such that $\frac {f(N)}{g(N)}\geq a$ for all $N\in \mathbb {Z}^+$
x _i	Thei -th vector in a sequence or thei -th coordinate ofx
∇f (x )	Gradient off atx
∇ _if (x )	$\frac {\partial f}{\partial {\mathbf {x}}_i}$
X _:j	Thej -th column of matrixX
X _ij	The entry at thei -th row and thej -th column ofX
X ^T	Transpose of matrixX
Diag(x )	Diagonal matrix whose diagonal entries are entries of
	vectorx
σ _i (X )	Thei -th largest singular value of matrixX
λ _i (X )	Thei -th largest eigenvalue of matrixX
\|X \|	Matrix whose (i ,j )-th entry is \|X _ij \|
Span(X )	The subspace spanned by the columns ofX
\|\|⋅\|\|	Operator norm of an operator or a matrix
\|\|⋅\|\| ₂ or ∥⋅∥	ℓ ₂ norm of vectors, $\|\|{\mathbf {v}}\|\|{ }_2=\sqrt {\sum _{i}{\mathbf {v}}_{i}^2}$ ;
	\|\|⋅\|\| is also used for general norm of vectors
\|\|⋅\|\| _∗	Nuclear norm of matrices, the sum of singular values
\|\|⋅\|\| ₀	ℓ ₀ pseudo-norm, number of nonzero entries
\|\|⋅\|\| ₁	ℓ ₁ norm, \|\|X \|\| ₁ =∑ _i ,j \|X _ij \|
\|\|⋅\|\| _p	ℓ _p norm, $\|\|\mathbf {X}\|\|{ }_p=\left (\sum _{i,j}\|{\mathbf {X}}_{ij}\|{ }^p\right )^{1/p}$
\|\|⋅\|\| _F	Frobenius norm of a matrix, $\|\|\mathbf {X}\|\|{ }_F=\sqrt {\sum _{i,j}{\mathbf {X}}_{ij}^2}$
\|\|⋅\|\| _∞	ℓ _∞ norm, \|\|X \|\| _∞ =max _ij \|X _ij \|
$\mbox{conv}(\mathbb {X})$	Convex hull of set $\mathbb {X}$
∂f	Subgradient (resp. supergradient) of a convex (resp
	concave) functionf
f ^∗	Optimum value off (x ), wherex varies in domf
	and the constraints
f ^∗ (x )	The conjugate function off (x )
Prox _αf (⋅)	Proximal mapping w.r.t.f and parameterα ,
	$\mbox{Prox}_{\alpha f}(\mathbf {y})= \operatorname *{\mathrm {argmin}}_{\mathbf {x}} \left (\alpha f(\mathbf {x})+\frac {1}{2}\\|\mathbf {x}-\mathbf {y}\\|{ }_2^2\right )$

A.2 Algebra and Probability

Proposition A.1 (Cauchy-Schwartz Inequality)

$\displaystyle \begin{aligned} \begin{array}{rcl} \left\langle\mathbf{x},\mathbf{y}\right\rangle \leq \|\mathbf{x}\|\|\mathbf{y}\|. \end{array} \end{aligned}$

Lemma A.1

For anyx ,y ,z, and $\mathbf {w}\in \mathbb {R}^{n}$ , we have the following three identities:

$\displaystyle \begin{aligned} \begin{array}{rcl} 2\left\langle\mathbf{x},\mathbf{y}\right\rangle&\displaystyle =&\displaystyle \|\mathbf{x}\|{}^2+\|\mathbf{y}\|{}^2-\|\mathbf{x}-\mathbf{y}\|{}^2,{} \end{array} \end{aligned}$

(A.1)

$\displaystyle \begin{aligned} \begin{array}{rcl} 2\left\langle\mathbf{x},\mathbf{y}\right\rangle&\displaystyle =&\displaystyle \|\mathbf{x}+\mathbf{y}\|{}^2-\|\mathbf{x}\|{}^2-\|\mathbf{y}\|{}^2,{} \end{array} \end{aligned}$

(A.2)

$\displaystyle \begin{aligned} \begin{array}{rcl} 2\left\langle\mathbf{x}-\mathbf{z},\mathbf{y}-\mathbf{w}\right\rangle&\displaystyle =&\displaystyle \|\mathbf{x}-\mathbf{w}\|{}^2-\|\mathbf{z}-\mathbf{w}\|{}^2-\|\mathbf{x}-\mathbf{y}\|{}^2+\|\mathbf{z}-\mathbf{y}\|{}^2.{} \end{array} \end{aligned}$

(A.3)

Definition A.1 ( Singular Value Decomposition (SVD) )

Suppose that $\mathbf {A} \in \mathbb {R}^{m\times n}$ with rankA = r . ThenA can be factorized as

$\displaystyle \begin{aligned} \mathbf{A}=\mathbf{U}\boldsymbol{\Sigma}{\mathbf{V}}^\top, \end{aligned}$

where $\mathbf {U} \in \mathbb {R}^{m\times r}$ satisfiesU ^⊤U = I , $\mathbf {V} \in \mathbb {R}^{n\times r}$ satisfiesV ^⊤V = I , andΣ = Diag(σ ₁ , ⋯ ,σ _r ), with

$\displaystyle \begin{aligned} \sigma_1\ge\sigma_2\ge\cdots\ge\sigma_r>0. \end{aligned}$

The factorization (1) is called theeconomic singular value decomposition (SVD) ofA . The columns ofU are calledleft singular vectors ofA , the columns ofV areright singular vectors , and the numbersσ _i are thesingular values .

Definition A.2 ( Laplacian Matrix of a Graph)

Denote a graph as $\mathfrak {g} = \{V, E \}$ , whereV andE are the node and the edge sets, respectively.e _ij = (i ,j ) ∈ E indicates that nodesi andj are connected. DefineV _i = {j ∈ V |(i ,j ) ∈ E } to be the index set of the nodes that are connected to nodei . The Laplacian matrix of the graph $\mathfrak {g} = \{V, E \}$ is defined as:

$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{L}}_{ij}=\left\{ \begin{array}{rcl} |V_i|, &\displaystyle &\displaystyle \text{if } i=j, \\ -1, &\displaystyle &\displaystyle \text{if } i\neq j \text{ and } (i,j)\in E, \\ 0, &\displaystyle &\displaystyle \text{otherwise}. \end{array} \right. \end{array} \end{aligned}$

Definition A.3 (Dual Norm)

Let ∥⋅∥ be a norm of vectors in $\mathbb {R}^n$ , then its dual norm ∥⋅∥ ^∗ is defined as:

$\displaystyle \begin{aligned} \begin{array}{rcl} \|\mathbf{y}\|{}^*=\max\{\left\langle\mathbf{x},\mathbf{y}\right\rangle|\|\mathbf{x}\|\leq 1\}. \end{array} \end{aligned}$

Proposition A.2

Given random vectorξ, we have

$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E}\|\boldsymbol{\xi}-\mathbb{E}\boldsymbol{\xi}\|{}^2\leq \mathbb{E}\|\boldsymbol{\xi}\|{}^2. \end{array} \end{aligned}$

Proposition A.3 ( Jensen’s Inequality : Continuous Case)

If $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is convex andξis a random vector over C, then

$\displaystyle \begin{aligned} \begin{array}{rcl} f(\mathbb{E}\boldsymbol{\xi})\leq \mathbb{E} f(\boldsymbol{\xi}). \end{array} \end{aligned}$

Definition A.4 (Discrete-Time Martingale)

A sequence of random variables (or random vectors)X ₁ ,X ₂ , ⋯ is called a martingale if it satisfies for any timen ,

$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E} |X_n| &\displaystyle <&\displaystyle \infty,\\ \mathbb{E}(X_{n+1}|X_1,\cdots,X_n)&\displaystyle =&\displaystyle X_n. \end{array} \end{aligned}$

That is, the conditional expected value of the next observation, given all the past observations, is equal to the most recent observation.

Proposition A.4 (Iterated Law of Expectation)

For two random variables X and Y , we have

$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E} Y = \mathbb{E}_X (\mathbb{E} (Y|X)). \end{array} \end{aligned}$

A.3 Convex Analysis

The descriptions for the basic concepts of convex sets and convex functions can be found in [ 4 ].

Definition A.5 (Convex Set)

A set $C \subseteq \mathbb {R}^n$ is called convex if for allx ,y ∈ C andα ∈ [0, 1] we haveαx + (1 − α )y ∈ C .

Definition A.6 (Extreme Point)

Given a nonempty convex setC , a vectorx ∈ C is said to be an extreme point ofC if it does not lie strictly between the endpoints of any line segment contained inC . Namely, there do not exist vectorsy ,z ∈ C , withy ≠ x andz ≠ x , and a scalarα ∈ (0, 1) such thatx = αy + (1 − α )z .

Definition A.7 (Convex Function)

A function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is called convex ifC is a convex set and for allx ,y ∈ C andα ∈ [0, 1] we have

$\displaystyle \begin{aligned} f(\alpha \mathbf{x} + (1 - \alpha)\mathbf{y})\leq \alpha f(\mathbf{x}) + (1 - \alpha) f(\mathbf{y}). \end{aligned}$

C is called the domain off .

Definition A.8 (Concave Function)

A function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is called concave if − f is convex.

Definition A.9 (Strictly Convex Function)

A function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is called strictly convex ifC is a convex set and for allx ≠ y ∈ C andα ∈ (0, 1) we have

$\displaystyle \begin{aligned} f(\alpha \mathbf{x} + (1 - \alpha)\mathbf{y}) < \alpha f(\mathbf{x}) + (1 - \alpha) f(\mathbf{y}). \end{aligned}$

Definition A.10 (Strongly Convex Function and Generally Convex Function)

A function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is called strongly convex ifC is a convex set and there exists a constantμ > 0 such that for allx ,y ∈ C andα ∈ [0, 1] we have

$\displaystyle \begin{aligned} f(\alpha \mathbf{x} + (1 - \alpha)\mathbf{y})\leq \alpha f(\mathbf{x}) + (1 - \alpha) f(\mathbf{y}) - \frac{\mu\alpha(1-\alpha)}{2}\|\mathbf{y}-\mathbf{x}\|{}^2. \end{aligned}$

μ is called thestrong convexity modulus off . For brevity, a strongly convex function with a strong convexity modulusμ is called aμ-strongly convex function . If a convex function is not strongly convex, we also call it agenerally convex function .

Proposition A.5 ( Jensen’s Inequality : Discrete Case)

If $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is convex,x _i ∈ C, α _i ≥ 0, i = 1, ⋯ ,m, and $\sum \limits _{i=1}^m \alpha _i=1$ , then

$\displaystyle \begin{aligned} \begin{array}{rcl} f\left(\sum_{i=1}^m \alpha_i {\mathbf{x}}_i\right)\leq \sum_{i=1}^m \alpha_i f({\mathbf{x}}_i). \end{array} \end{aligned}$

Definition A.11 (Smooth Function)

A function is (informally) called smooth if it is continuously differentiable.

Definition A.12 (Function with Lipschitz Continuous Gradients)

A differentiable function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is called to have Lipschitz continuous gradients if there existsL > 0 such that

$\displaystyle \begin{aligned} \|\nabla f(\mathbf{x})-\nabla f(\mathbf{y})\| \leq L \|\mathbf{y}-\mathbf{x}\|,\quad \forall \mathbf{x},\mathbf{y}\in C. \end{aligned}$

For simplicity, if the constantL is explicitly specified we also call such a function anL-smooth function .

Definition A.13 (Function with Coordinate Lipschitz Continuous Gradients)

f (x ) is said to haveL _c -coordinate Lipschitz continuous gradients if:

$\displaystyle \begin{aligned} \begin{array}{rcl}{} |\nabla_i f(\mathbf{x}) - \nabla_i f(\mathbf{y}) |\leq L_c|{\mathbf{x}}_i -{\mathbf{y}}_i |,\quad \text{all } i \in [n]. \end{array} \end{aligned}$

(A.4)

Definition A.14 (Function with Lipschitz Continuous Hessians)

A twice differentiable function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is called to have Lipschitz continuous Hessians if there existsL > 0 such that

$\displaystyle \begin{aligned} \|\nabla^2 f(\mathbf{x})-\nabla^2 f(\mathbf{y})\| \leq L \|\mathbf{y}-\mathbf{x}\|,\quad \forall \mathbf{x},\mathbf{y}\in C. \end{aligned}$

If the constantL is explicitly specified such a function is also called to haveL -Lipschitz continuous Hessians.

Proposition A.6 ([ 6 ])

If $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is L-smooth, then

$\displaystyle \begin{aligned} \begin{array}{rcl} \left|f(\mathbf{y})- f(\mathbf{x})-\left\langle\nabla f(\mathbf{x}),\mathbf{y}-\mathbf{x}\right\rangle\right|\leq \frac{L}{2}\|\mathbf{y}-\mathbf{x}\|{}^2,\quad \forall \mathbf{x},\mathbf{y}\in C.{} \end{array} \end{aligned}$

(A.5)

In particular, if $\mathbf {y}=\mathbf {x}-\frac {1}{L}\nabla f(\mathbf {x})$ , then

$\displaystyle \begin{aligned} \begin{array}{rcl}{} f(\mathbf{y})\leq f(\mathbf{x})-\frac{1}{2L}\|\nabla f(\mathbf{x})\|{}^2. \end{array} \end{aligned}$

(A.6)

If f is further convex, then

$\displaystyle \begin{aligned} \begin{array}{rcl} f(\mathbf{y})\geq f(\mathbf{x})+\left\langle\nabla f(\mathbf{x}),\mathbf{y}-\mathbf{x}\right\rangle+\frac{1}{2L}\|\nabla f(\mathbf{y})-\nabla f(\mathbf{x})\|{}^2.{} \end{array} \end{aligned}$

(A.7)

Proposition A.7

If $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ has L _c-coordinate Lipschitz continuous gradients on coordinate i andxandyonly differ at the i-th entry, then we have

$\displaystyle \begin{aligned} \begin{array}{rcl} \left|f(\mathbf{x})- f(\mathbf{y}) -\langle\nabla_{i} f(\mathbf{y}), {\mathbf{x}}_{i}-{\mathbf{y}}_{i}\rangle \right|\leq \frac{L_c}{2}\left({\mathbf{x}}_{i}-{\mathbf{y}}_{i} \right)^2. \end{array} \end{aligned}$

Proposition A.8

If $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ has L-Lipschitz continuous Hessians, then [ 6]

$\displaystyle \begin{aligned} \left|f(\mathbf{y})-f(\mathbf{x})-\left\langle\nabla f(\mathbf{x}),\mathbf{y}-\mathbf{x}\right\rangle-\frac{1}{2}(\mathbf{y}-\mathbf{x})^T\nabla^2 f(\mathbf{x})(\mathbf{y}-\mathbf{x})\right|\leq& \frac{L}{6}\|\mathbf{y}-\mathbf{x}\|{}^2,\notag\\ &\forall \mathbf{x},\mathbf{y}\in C.{} \end{aligned}$

(A.8)

Definition A.15 (Subgradient of a Convex Function)

A vectorg is called a subgradient of a convex function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ atx ∈ C if

$\displaystyle \begin{aligned}f(\mathbf{y})\geq f(\mathbf{x})+\left\langle\mathbf{g},\mathbf{y}-\mathbf{x}\right\rangle,\forall \mathbf{y}\in C.\end{aligned}$

The set of subgradients atx is denoted as∂f (x ).

Proposition A.9

For convex function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ , its subgradient exists at every interior point of C. It is differentiable atxiff (aka if and only if) ∂f (x )is a singleton.

Proposition A.10

If $f: \mathbb {R}^n \rightarrow \mathbb {R}$ is μ-strongly convex, then

$\displaystyle \begin{aligned} \begin{array}{rcl}{} f(\mathbf{y})\geq f(\mathbf{x})+\left\langle\mathbf{g},\mathbf{y}-\mathbf{x}\right\rangle+\frac{\mu}{2}\|\mathbf{y}-\mathbf{x}\|{}^2,\quad \forall \mathbf{g}\in\partial f(\mathbf{x}). \end{array} \end{aligned}$

(A.9)

In particular, if f is differentiable and μ-strongly convex and ${\mathbf {x}}^*= \operatorname *{\mathrm {argmin}}_{\mathbf {x}}f(\mathbf {x})$ , then

$\displaystyle \begin{aligned} \begin{array}{rcl}{} f(\mathbf{x})-f({\mathbf{x}}^*)\geq \frac{\mu}{2}\|\mathbf{x}-{\mathbf{x}}^*\|{}^2. \end{array} \end{aligned}$

(A.10)

On the other hand, we can have

$\displaystyle \begin{aligned} \begin{array}{rcl}{} f({\mathbf{x}}^*)\geq f(\mathbf{x})-\frac{1}{2\mu}\|\nabla f(\mathbf{x})\|{}^2. \end{array} \end{aligned}$

(A.11)

Definition A.16 (Epigraph)

The epigraph of $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is defined as

$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{epi}\,f =\{(\mathbf{x},t)|\mathbf{x}\in C, t\geq f(\mathbf{x})\}. \end{array} \end{aligned}$

Definition A.17 (Closed Function)

If epif is a closed set, thenf is called a closed function.

Definition A.18 (Monotone Mapping and Monotone Function)

A set valued function $f: C \subseteq \mathbb {R}^n \rightarrow 2^{\mathbb {R}^n}$ is called a monotone mapping if

$\displaystyle \begin{aligned} \begin{array}{rcl} \left\langle\mathbf{x}-\mathbf{y},{\mathbf{u}}-{\mathbf{v}}\right\rangle\geq 0, \quad \forall \mathbf{x},\mathbf{y}\in C\mbox{ and } {\mathbf{u}}\in f(\mathbf{x}),{\mathbf{v}}\in f(\mathbf{y}). \end{array} \end{aligned}$

In particular, iff is a single valued function and

$\displaystyle \begin{aligned} \begin{array}{rcl} \left\langle\mathbf{x}-\mathbf{y},f(\mathbf{x})-f(\mathbf{y})\right\rangle\geq 0, \quad \forall \mathbf{x},\mathbf{y}\in C. \end{array} \end{aligned}$

then it is called a monotone function.

Proposition A.11 ( Monotonicity of Subgradient)

If $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ is convex, then ∂f (x )is a monotone mapping. If f is further μ-strongly convex, then

$\displaystyle \begin{aligned} \begin{array}{rcl} \left\langle{\mathbf{x}}_1-{\mathbf{x}}_2,{\mathbf{g}}_1-{\mathbf{g}}_2\right\rangle\geq \mu\|{\mathbf{x}}_1-{\mathbf{x}}_2\|{}^2, \quad \forall {\mathbf{x}}_i\in C\mathit{\mbox{ and }}{\mathbf{g}}_i\in\partial f({\mathbf{x}}_i), i=1,2. \end{array} \end{aligned}$

Definition A.19 (Envelope Function and Proximal Mapping )

Given a function $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ anda > 0,

$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Env}_{a f}(\mathbf{x})=\min\limits_{\mathbf{y}\in C} \left(f(\mathbf{y})+\frac{1}{2a}\|\mathbf{y}-\mathbf{x}\|{}^2\right) \end{array} \end{aligned}$

is called the envelope function off (x ), and

$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Prox}_{a f}(\mathbf{x})=\operatorname*{\mathrm{argmin}}\limits_{\mathbf{y}\in C} \left(f(\mathbf{y})+\frac{1}{2a}\|\mathbf{y}-\mathbf{x}\|{}^2\right) \end{array} \end{aligned}$

is called the proximal mapping off (x ). Prox _af (x ) may be set-valued iff is not convex.

Further descriptions of proximal mapping can be found in [ 7 ].

Definition A.20 ( Bregman Distance )

Given a differentiable strongly convex functionh , the Bregman distance is defined as

$\displaystyle \begin{aligned} \begin{array}{rcl} D_h(\mathbf{y},\mathbf{x})=h(\mathbf{y})-h(\mathbf{x})-\left\langle\nabla h(\mathbf{x}),\mathbf{y}-\mathbf{x}\right\rangle. \end{array} \end{aligned}$

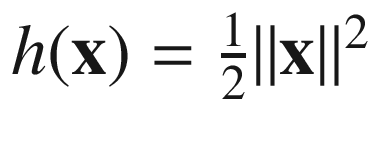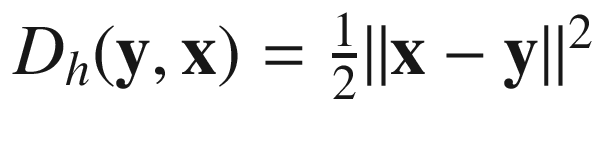The Euclidean distance is obtained when $h(\mathbf {x})=\frac {1}{2}\|\mathbf {x}\|{ }^2$ , in which case $D_h(\mathbf {y},\mathbf {x})=\frac {1}{2}\|\mathbf {x}-\mathbf {y}\|{ }^2$ . The generalization to a nondifferentiableh was discussed in [ 5 ].

Definition A.21 ( Conjugate Function )

Given $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ , its conjugate function is defined as

$\displaystyle \begin{aligned} \begin{array}{rcl} f^*({\mathbf{u}})=\operatorname*{\mathrm{sup}}_{\mathbf{z}\in C}\left(\left\langle\mathbf{z},{\mathbf{u}}\right\rangle-f(\mathbf{z})\right). \end{array} \end{aligned}$

The domain off ^∗ is

$\displaystyle \begin{aligned}\mbox{dom} f^* =\{{\mathbf{u}}|f^*({\mathbf{u}})<+\infty\}.\end{aligned}$

Proposition A.12 (Properties of Conjugate Function )

Given $f: C \subseteq \mathbb {R}^n \rightarrow \mathbb {R}$ , its conjugate function has the following properties:

1.
f ^∗is always a convex function;
2.
f ^∗∗ (x ) ≤ f (x ), ∀x ∈ C;
3.
If f is a proper, closed and convex function, then f ^∗∗ (x ) = f (x ), ∀x ∈ C.
4.
If f is L-smooth, then f ^∗is L ⁻¹-strongly convex on domf ^∗. Conversely, if f is μ-strongly convex, then f ^∗is μ ⁻¹-smooth on domf ^∗ .
5.
If f is closed and convex, theny ∈ ∂f (x )if and only ifx ∈ ∂f ^∗ (y ).

Proposition A.13 ( Fenchel-Young Inequality )

Let f ^∗be the conjugate function of f, then

$\displaystyle \begin{aligned}f(\mathbf{x})+f^*(\mathbf{y})\geq \left\langle\mathbf{x},\mathbf{y}\right\rangle.\end{aligned}$

Definition A.22 ( Lagrangian Function )

Given a constrained problem:

$\displaystyle \begin{aligned} \begin{array}{rcl}{} \min_{\mathbf{x}\in\mathbb{R}^n}&\displaystyle &\displaystyle f(\mathbf{x}),\\ s.t.&\displaystyle &\displaystyle \mathbf{A}\mathbf{x}={\mathbf{b}},\\ &\displaystyle &\displaystyle \mathbf{g}(\mathbf{x})\leq \mathbf{0}, \end{array} \end{aligned}$

(A.12)

where $\mathbf {A}\in \mathbb {R}^{m\times n}$ andg (x ) = (g ₁ (x ), ⋯ ,g _p (x )) ^T , the Lagrangian function is

$\displaystyle \begin{aligned} \begin{array}{rcl} L(\mathbf{x},{\mathbf{u}},{\mathbf{v}})=f(\mathbf{x})+\left\langle{\mathbf{u}},\mathbf{A}\mathbf{x}-{\mathbf{b}}\right\rangle+\left\langle{\mathbf{v}},\mathbf{g}(\mathbf{x})\right\rangle,\notag \end{array} \end{aligned}$

wherev ≥0 .

Definition A.23 ( Lagrange Dual Function )

Given a constrained problem ( A.12 ), the Lagrange dual function is

$\displaystyle \begin{aligned} \begin{array}{rcl}{} d({\mathbf{u}},{\mathbf{v}})=\min_{\mathbf{x}\in C}L(\mathbf{x},{\mathbf{u}},{\mathbf{v}}), \end{array} \end{aligned}$

(A.13)

whereC is the domain off . The domain of the dual function is $\mathbb {D}=\{({\mathbf {u}},{\mathbf {v}})|d({\mathbf {u}},{\mathbf {v}})>-\infty \}$ .

Definition A.24 (Dual Problem)

Given a constrained problem ( A.12 ), the dual problem is

$\displaystyle \begin{aligned} \begin{array}{rcl} \max_{{\mathbf{u}},{\mathbf{v}}}&\displaystyle &\displaystyle d({\mathbf{u}},{\mathbf{v}}),\\ s.t.&\displaystyle &\displaystyle {\mathbf{v}}\geq \mathbf{0}. \end{array} \end{aligned}$

Accordingly, problem ( A.12 ) is called the primal problem.

Definition A.25 ( Slater’s Condition )

For convex primal problem ( A.12 ), if there exists anx ₀ such thatAx ₀ = b , $g_i({\mathbf {x}}_0)\leq 0,i\in \mathbb {I}_1$ , and $g_i({\mathbf {x}}_0)< 0,i\in \mathbb {I}_2$ , where $\mathbb {I}_1$ and $\mathbb {I}_2$ are the sets of indices of linear and nonlinear inequality constraints, respectively, then the Slater’s condition holds.

Proposition A.14 (Properties of Dual Problem)

1.
d (u ,v )is always a concave function even if the primal problem ( A.12 )is not convex.
2.
The primal and the dual optimal values, f ^∗and d ^∗, always satisfy the weak duality: f ^∗ ≥ d ^∗ .
3.
When the Slater’s condition holds, the strong duality holds: f ^∗ = d ^∗ .

Definition A.26 ( KKT Point and KKT Condition )

(x ,u ,v ) is called a Karush–Kuhn–Tucker (KKT) point of problem ( A.12 ) if

1.
Stationarity: $\mathbf {0}\in \partial f(\mathbf {x})+{\mathbf {A}}^T{\mathbf {u}}+\sum _{i=1}^p{\mathbf {v}}_i\partial g_i(\mathbf {x})$ .
2.
Primal feasibility:Ax = b ,g _i (x ) ≤ 0,i = 1, ⋯ ,p .
3.
Complementary slackness:v _ig _i (x ) = 0.
4.
Dual feasibility:v _i ≥0 ,i = 1, ⋯ ,p .

The above conditions are called the KKT condition of problem ( A.12 ). They are the optimality condition of problem ( A.12 ) whenf (x ) andg _i (x ),i = 1, ⋯ ,p , are all convex.

Proposition A.15

When f (x )and g _i (x ), i = 1, ⋯ ,p, are all convex, (x ^∗ ,u ^∗ ,v ^∗ )is a pair of the primal and the dual solutions with zero dual gap if and only if it satisfies the KKT condition .

Definition A.27 (Compact Set )

A subsetS of $\mathbb {R}^n$ is called compact if it is both bounded and closed.

Definition A.28 (Convex Hull)

The convex hull of a set $\mathbb {X}$ , denoted as $\mbox{conv}(\mathbb {X})$ , is the set of all convex combinations of points in $\mathbb {X}$ :

$\displaystyle \begin{aligned}\mbox{conv}(\mathbb{X})=\left\{\left.\sum_{i=1}^k \alpha_i{\mathbf{x}}_i\right|{\mathbf{x}}_i\in\mathbb{X},\alpha_i\geq0,i=1,\cdots,k,\sum_{i=1}^k \alpha_i=1\right\}.\end{aligned}$

Theorem A.1 ( Danskin’s Theorem )

Let $\mathbb {Z}$ be a compact subset of $\mathbb {R}^m$ , and let $\phi :\mathbb {R}^n\times \mathbb {Z}\rightarrow \mathbb {R}$ be continuous and such that $\phi (\cdot ,\mathbf {z}):\mathbb {R}^n\rightarrow \mathbb {R}$ is convex for each $\mathbf {z}\in \mathbb {Z}$ . Define $f:\mathbb {R}^n\rightarrow \mathbb {R}$ by $f(\mathbf {x})=\max \limits _{\mathbf {z}\in \mathbb {Z}}\phi (\mathbf {x},\mathbf {z})$ and

$\displaystyle \begin{aligned}\mathbb{Z}(\mathbf{x})=\left\{\bar{\mathbf{z}}\left|\phi(\mathbf{x},\bar{\mathbf{z}})=\max\limits_{\mathbf{z}\in\mathbb{Z}}\phi(\mathbf{x},\mathbf{z})\right.\right\}.\end{aligned}$

If ϕ (⋅,z )is differentiable for all $\mathbf {z}\in \mathbb {Z}$ and ∇ _xϕ (x , ⋅)is continuous on $\mathbb {Z}$ for eachx, then

$\displaystyle \begin{aligned}\partial f(\mathbf{x})=\mathit{\mbox{conv}}\left\{\nabla_x \phi(\mathbf{x},\mathbf{z})|\mathbf{z}\in\mathbb{Z}(\mathbf{x})\right\},\quad \forall \mathbf{x}\in\mathbb{R}^n.\end{aligned}$

Definition A.29 ( Saddle Point )

(x ^∗ ,λ ^∗ ) is called a saddle point of function $f(\mathbf {x},\boldsymbol {\lambda }): C\times D\rightarrow \mathbb {R}$ if it satisfies the following inequalities:

$\displaystyle \begin{aligned} f({\mathbf{x}}^*,\boldsymbol{\lambda}) \leq f({\mathbf{x}}^*,\boldsymbol{\lambda}^*) \leq f(\mathbf{x},\boldsymbol{\lambda}^*), \quad \forall \mathbf{x}\in C, \boldsymbol{\lambda} \in D. \end{aligned}$

A.4 Nonconvex Analysis

Definition A.30 (Proper Function)

A function $g:\mathbb R^n\rightarrow (-\infty ,+\infty ]$ is said to be proper if domg ≠ ∅, where dom $g=\{\mathbf {x}\in \mathbb R:g(\mathbf {x})<+\infty \}$ .

Definition A.31 (Lower Semicontinuous Function)

A function $g:\mathbb R^n\rightarrow (-\infty ,+\infty ]$ is said to be lower semicontinuous at pointx ₀ if

$\displaystyle \begin{aligned} \liminf_{\mathbf{x}\rightarrow {\mathbf{x}}_0} g(\mathbf{x})\geq g({\mathbf{x}}_0).\notag \end{aligned}$

Definition A.32 (Coercive Function)

F (x ) is called coercive if inf _xF (x ) > −∞ and {x |F (x ) ≤ a } is bounded for alla .

Definition A.33 (Subdifferential)

Letf be a proper and lower semicontinuous function.

1.
For a givenx ∈domf , the Frechel subdifferential off atx , written as $\hat \partial f(\mathbf {x})$ , is the set of all vectors ${\mathbf {u}}\in \mathbb R^n$ which satisfies
$\displaystyle \begin{aligned} \liminf_{\mathbf{y} \neq\mathbf{x},\mathbf{y}\rightarrow\mathbf{x}} \frac{f(\mathbf{y})-f(\mathbf{x})-\left\langle{\mathbf{u}},\mathbf{y}-\mathbf{x}\right\rangle}{\|\mathbf{y}-\mathbf{x}\|}\geq 0.\notag \end{aligned}$
2.
The limiting subdifferential, or simply the subdifferential, off at $\mathbf {x}\in \mathbb R^n$ , written as∂f (x ), is defined through the following closure process:
$\displaystyle \begin{aligned} \begin{array}{rcl} \partial f(\mathbf{x}):=\{{\mathbf{u}}\in\mathbb R^n:\exists {\mathbf{x}}_k\rightarrow \mathbf{x},f({\mathbf{x}}_k)\rightarrow f(\mathbf{x}),{\mathbf{u}}_k\in\hat\partial f({\mathbf{x}}_k)\rightarrow{\mathbf{u}},k\rightarrow \infty\}.\notag \end{array} \end{aligned}$

Definition A.34 ( Critical Point )

A pointx is called a critical point of functionf if0 ∈ ∂f (x ).

The following lemma describes the properties of subdifferential.

Lemma A.2

1.
In the nonconvex context, Fermat’s rule remains unchanged: If $\mathbf {x}\in \mathbb R^n$ is a local minimizer of g, then0 ∈ ∂g (x ).
2.
Let (x _k ,u _k )be a sequence such thatx _k →x,u _k →u, g (x _k ) → g (x ), andu _k ∈ ∂g (x _k ), thenu ∈ ∂g (x ).
3.
If f is a continuously differentiable function, then ∂ (f + g )(x ) = ∇f (x ) + ∂g (x ).

Definition A.35 ( Desingularizing Function )

A function $\varphi :[0,\eta )\rightarrow \mathbb R^+$ satisfying the following conditions is called a desingularizing function:

(1)
φ is concave and continuously differentiable on (0,η );
(2)
φ is continuous at 0,φ (0) = 0; and
(3)
φ′ (x ) > 0, ∀x ∈ (0,η ).

Φ _η is the set of desingularizing functions defined on [0,η ).

Now we define the KŁ function . More introductions and applications can be found in [ 1 – 3 ].

Definition A.36 (Kurdyka–Łojasiewicz (KŁ) Property)

A function $f:\mathbb R^n \rightarrow (-\infty ,+\infty ]$ is said to have the Kurdyka-Łojasiewicz (KŁ) property at $\overline {\mathbf {u}}\in$ dom $\partial f:=\{\mathbf {x}\in \mathbb R^n:\partial f({\mathbf {u}})\neq \emptyset \}$ if there existsη ∈ (0, +∞ ], a neighborhoodU of $\overline {\mathbf {u}}$ , and a desingularizing function φ ∈ Φ _η , such that for all

$\displaystyle \begin{aligned} {\mathbf{u}}\in U\cap \{{\mathbf{u}}\in \mathbb R^n:f(\overline {\mathbf{u}})<f({\mathbf{u}})<f(\overline {\mathbf{u}})+\eta\},\notag \end{aligned}$

the following inequality holds:

$\displaystyle \begin{aligned} \varphi'(f({\mathbf{u}})-f(\overline{\mathbf{u}}))\mbox{dist}(\mathbf{0},\partial f({\mathbf{u}}))>1.\notag \end{aligned}$

Lemma A.3 (Uniform Kurdyka-Łojasiewicz Property)

Let Ω be a compact set and let $f:\mathbb R^n \rightarrow (-\infty ,+\infty ]$ be a proper and lower semicontinuous function. Assume that f is constant on Ω and satisfies the KŁ property at each point of Ω. Then there exists 𝜖 > 0, η > 0, and φ ∈Φ _η, such that for all $\overline {\mathbf {u}}$ in Ω and alluin the following intersection

$\displaystyle \begin{aligned} \{{\mathbf{u}}\in \mathbb R^n:\mathrm{dist}({\mathbf{u}},\Omega)<\epsilon\}\cap \{{\mathbf{u}}\in \mathbb R^n:f(\overline {\mathbf{u}})<f({\mathbf{u}})<f(\overline {\mathbf{u}})+\eta\},\notag \end{aligned}$

the following inequality holds:

$\displaystyle \begin{aligned} \varphi'(f({\mathbf{u}})-f(\overline{\mathbf{u}}))\mathrm{dist}(\mathbf{0},\partial f({\mathbf{u}}))>1.\notag \end{aligned}$

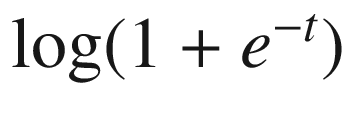Functions satisfying the KŁ property are general enough. Typical examples include: real polynomial functions, logistic loss function $\log (1+e^{-t})$ , ∥x ∥ _p (p ≥ 0), ∥x ∥ _∞ , and indicator functions of the positive semidefinite (PSD) cone, the Stiefel manifolds, and the set of constant rank matrices.

References

1.
H. Attouch, J. Bolte, P. Redont, A. Soubeyran, Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res.35 (2), 438–457 (2010) MathSciNetCrossref
2.
H. Attouch, J. Bolte, B.F. Svaiter, Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Math. Program.137 (1–2), 91–129 (2013) MathSciNetCrossref
3.
J. Bolte, S. Sabach, M. Teboulle, Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program.146 (1–2), 459–494 (2014) MathSciNetCrossref
4.
S. Boyd, L. Vandenberghe,Convex Optimization (Cambridge University Press, Cambridge, 2004) Crossref
5.
K.C. Kiwiel, Proximal minimization methods with generalized Bregman functions. SIAM J. Control. Optim.35 (4), 1142–1168 (1997) MathSciNetCrossref
6.
Y. Nesterov,Introductory Lectures on Convex Optimization: A Basic Course (Springer, New York, 2004) Crossref
7.
N. Parikh, S. Boyd, Proximal algorithms. Found. Trends Optim.1 (3), 127–239 (2014) Crossref

Index

Accelerated alternating direction method of multiplier (Acc-ADMM)

Accelerated augmented Lagrange multiplier method

Accelerated dual ascent

Accelerated gradient descent (AGD)

Accelerated Lagrange multiplier method

Accelerated linearized augmented Lagrangian method

Accelerated linearized penalty method

Accelerated penalty method

Accelerated primal-dual method

Accelerated proximal gradient (APG)

Accelerated proximal point method

Accelerated stochastic alternating direction method of multiplier (Acc-SADMM)

Accelerated stochastic coordinate descent (ASCD)

Accelerated stochastic dual coordinate ascent (Acc-SDCA)

Almost convex AGD (AC-AGD)

Alternating direction method of multiplier (ADMM)

Asynchronous accelerated coordinate descent (AACD)

Asynchronous accelerated gradient descent (AAGD)

Asynchronous accelerated stochastic coordinate descent (AASCD)

Asynchronous gradient descent

Asynchronous stochastic coordinate descent

Asynchronous stochastic gradient descent (ASGD)

Asynchronous stochastic variance reduced gradient (ASVRG)

Augmented Lagrange multiplier method

Augmented Lagrangian function

Black-box acceleration

Bregman distance

Bregman Lagrangian

Catalyst

Compact set

Composite optimization

Conjugate function

Continuation technique

Critical point

Danskin’s theorem

Desingularizing function

Distributed accelerated gradient descent

Distributed ADMM

Distributed dual ascent

Distributed dual coordinate ascent

Distributed stochastic communication accelerated dual (DSCAD)

Dual norm

Dual problem

Ergodic

Estimate function

Estimate sequence

Euler method

Exact first-order algorithm (EXTRA)

Faster Frank–Wolfe method

Fenchel-Young inequality

Frank-Wolfe method

Gossip matrix

Hölderian error bound condition

Heavy-ball method

High order accelerated gradient descent

Incremental first-order oracle (IFO)

Inexact accelerated gradient descent

Inexact accelerated proximal gradient

Inexact accelerated proximal point method

Inexact proximal mapping

Jensen’s inequality

Katyusha

KKT condition

KKT point

Kurdyka-Łojasiewicz (KŁ) condition/property

KŁ function

Lagrange dual function

Lagrange multiplier method

Lagrangian function

Laplacian matrix

Linearized alternating direction method of multiplier (Linearized ADMM)

Lyapunov function

Minimization by incremental surrogate optimization (MISO)

Mirror descent

Momentum

Momentum compensation

Monotone APG

Monotonicity

Negative curvature descent (NCD)

Negative curvature search (NC-Search)

Nesterov–Polyak method

Non-ergodic

Nonconvex AGD

Performance estimation problem

Primal-dual gap

Primal-dual method

Proximal mapping

Quadratic functional growth

Restart

Saddle point

Singular value decomposition (SVD)

Slater’s condition

Stochastic accelerated gradient descent (SAGD)

Stochastic average gradient (SAG)

Stochastic coordinate descent (SCD)

Stochastic dual coordinate ascent (SDCA)

Stochastic gradient descent (SGD)

Stochastic path-integrated differential estimator (SPIDER)

Stochastic primal-dual method

Stochastic variance reduced gradient (SVRG)

Strongly convex set

Variance reduction (VR)