CHAPTER 2

A BASIC INTRODUCTION TO DIMENSIONAL ANALYSIS APPLIED TO UNIT CONVERSION

2.1 WHAT ARE THE BASE AND THE DERIVED UNITS PRESENTED HEREIN?

A physical quantity comprises a numerical value (e.g., 43) and an associated unit (i.e., meters). The aforementioned physical quantity constitutes one of the base SI units (meter) with the amplitude as defined by the attached numerical value (43). In the SI Unit System there are seven (7) base units. The SI Base Units are as shown in Table 2-1 {30}:

TABLE 2-1

Quantity	Unit Name	Symbol
length	meter	m
mass(a)	kilogram	kg
time	second	s
electric current	ampere	A
thermodynamic temperature	kelvin	K
amount of substance	mole	mol
luminous intensity	candela	cd
(a) United States standard practice for laws and regulations, “weight” is a synonym for mass.

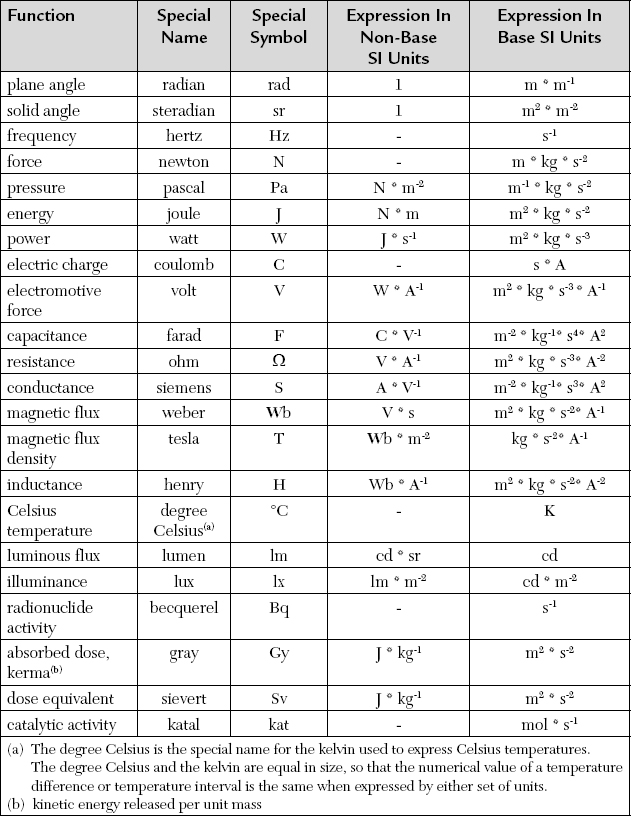
The SI derived units used in science, engineering, and mathematics disciplines are formed by combining the base units algebraically. The use of derived units is to improve the ease of calculation and to allow for improved problem concept understanding. In the case of commonly used derived units, the International System of Units has assigned special names to 22 of the most frequently used derived units, two of which are the dimensionless units (radian (rad) and steradian (sr)) (see Table 2-2 {31}).

TABLE 2-2

The rules of physical analysis and algebra require that for all dimensional mathematical equations {32}, the results of the combined resolved {33} elements on each side of the equality statement (=) must be numerically and unitarily {34} coherent {35} (see Example 1).

Linear Velocity Example 1:

where:

The linear dimension of 1 inch in the Inch-Pound Units system is defined as being equal to 2.54 centimeters in the SI system and the magnitude of the unit second (s) is equal in both systems. In the process of conversion, the conversion factor cancels the redundant unit factors (in and 1/in), as shown.