CHAPTER 3
AN INTRODUCTION TO THE INTERNATIONAL SYSTEM OF UNITS (SI) – Conversion Factors for General Use (Bidirectional Conversion App Section)
In the NIST Special Publication 1038{36}, the International System of Units (SI) – Conversion Factors for General Use are defined. Conversion factors are the mathematical multiplier or divisor and associated units that allow any compatible measurements to be converted from one system of units to another system of units (e.g., inches to centimeters or vice versa). As with any measurement, caution needs to be applied so that resolution (number of digits) is not confused with accuracy (number of significant digits). The general rule of thumb (first approximation) is to use no more digits than are absolutely necessary. See the Appendix for more details on significant digits.
The examples below demonstrate calculations as applied to obtain the results shown by the Unit Convertor MATLAB App provided with this book.
3.1 QUANTITIES OF SPACE/TIME
Figure 3.1-0 shows the Unit Converter MATLAB App Front Panel with the Space/Time Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Tabs available in the App is explored herein.

FIGURE 3.1-0 Unit Converter Using MATLAB App - Front Panel - Space/Time Tab.
Length Tab
The first Minor Tab under the Space/Time Major Tab is the Length Tab (see Figure 3.1-1). This example demonstrates the conversion of Nautical Miles to Fathoms. In this example, the amplitude of Nautical Miles is set equal to one (1.0). The conversion equation is shown in Example 3.1-1 {37}.
Nautical Miles (nmi) (=1.0) to Fathoms (ftm) Example 3.1-1:
ftm |
= |
nmi * km/nmi * m/km * ftm/m = nmi * 1.852 * 1000 * 1/1.828804 |
= |
nmi * 1.01268370E3 |
Where: ftm |
= |
the number of fathoms calculated |
nmi |
= |
the number of nautical miles to be converted (1.0) |
km/nmi |
= |
the conversion factor from nautical miles to kilometers (1.852) |
m/km |
= |
the conversion factor from kilometers to meters (1000) |
ftm/m |
= |
the conversion factor from meters to fathoms (1/1.828804) |
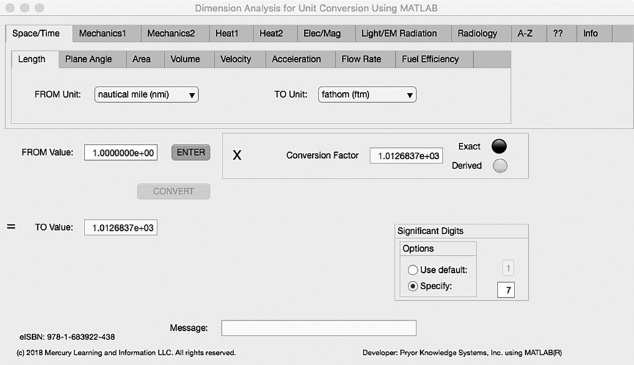
FIGURE 3.1-1 Unit Converter Using MATLAB App - - Space/Time Length Tab.
And:
The resulting solution is:
ftm |
= |
1.0 * 1.01268370E3 = 1.01268370E3 Fathoms |
(3.1-1) |
The Space/Time Length Tab allows the bidirectional selection of the following length dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Length | ||
| nautical mile (nmi) | ||
| mile (mi) | ||
| kilometer (km) | ||
| fathom (ftm) | ||
| yard (yd) | ||
| meter (m) | ||
| foot (ft) | ||
| foot (U.S. Survey) | ||
| inch (in) | ||
| centimeter (cm) | ||
| millimeter (mm) | ||
| pica, printer’s (12p) | ||
| point, printer’s (p) | ||
| mil (0.001 in) | ||
| micrometer (µm) | ||
| microinch (µin) | ||
| nanometer (nm) | ||
| angstrom |
Plane Angle Tab
The second Minor Tab under the Space/Time Major Tab is the Plane Angle Tab (see Figure 3.1-2). This example shows the conversion of Radian to degree arc. In this example, the amplitude of Radian is set equal to one (1.0). The conversion equation is shown in Example 3.1-2.
Radian (rad) to degree arc (°) Example 3.1-2:
degree arc = rad * degrees/rad = rad * 57.29578 = 57.29578 degrees
Where: degree arc |
= |
the number of degrees calculated |
rad |
= |
the starting number of Radian (1.0) |
degrees/rad |
= |
the conversion factor from Radian to degrees (57.29578) |
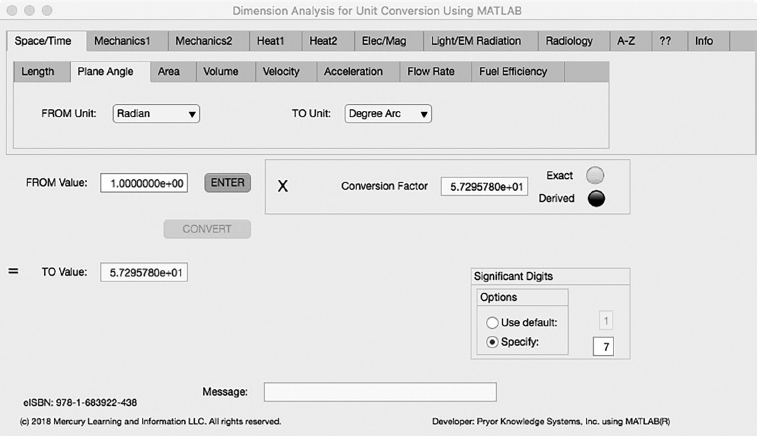
FIGURE 3.1-2 Unit Converter Using MATLAB App - Space/Time Plane Angle Tab.
And:
The resulting solution is:
degree arc = 1.0 * 57.29578 = 57.29578 degrees |
(3.1-2) |
The Space/Time Plane Angle Tab allows the bidirectional selection of the following angle dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Plane Angle | ||
| Radian | ||
| Degree Arc |
Area Tab
The third Minor Tab under the Space/Time Major Tab is the Area Tab (see Figure 3.1-3). This example shows the conversion of Square Feet to Square Kilometers. In this example, the amplitude of Square Feet is set equal to one (1.0). The conversion equation is shown in Example 3.1-3.
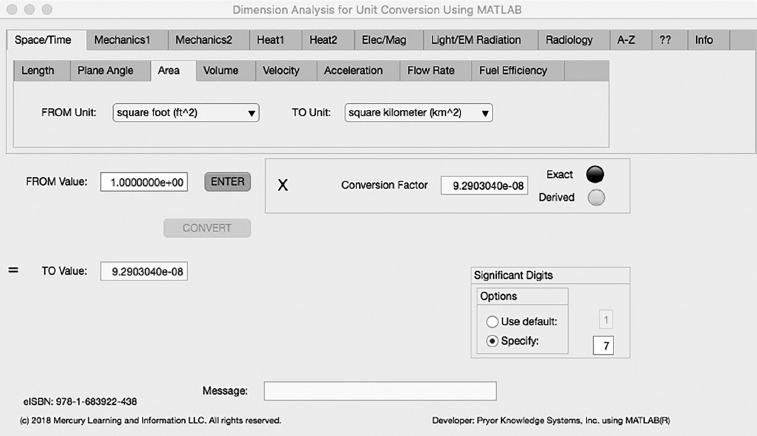
FIGURE 3.1-3 Unit Converter Using MATLAB App - Space/Time Area Tab.
Square Feet (ft2) (=1.0) to Square Kilometers (km2) Example 3.1-3:
km2 |
= |
ft2 * m2/ ft2 * km2/ m2 = ft2 * 9.290304E-2 * 1/ 1.0E6 |
= |
ft2 * 9.290304E-8 |
Where: km2 |
= |
the number of Square Kilometers calculated |
ft2 |
= |
the number of Square Feet to be converted (1.0) |
m2/ft2 |
= |
the conversion factor from Square Feet to Square Meters (9.290304E-2) |
km2/m2 |
= |
the conversion factor from Square Meters to Square Kilometers (1/ 1.0E6) |
And:
The resulting solution is:
km2 = 1.0 * 9.290304E-8 = 9.290304E-8 Square Kilometers |
(3.1-3) |
The Space/Time Area Tab allows the bidirectional selection of the following area dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Area | ||
| square mi (mi^2) | ||
| square km (km^2) | ||
| hectare (ha) | ||
| acre | ||
| square m (m^2) | ||
| square yd (yd^2) | ||
| square ft (ft^2) | ||
| square in (in^2) | ||
| square cm (cm^2) | ||
| square mm (mm^2) | ||
| circular mil |
Volume Tab
The fourth Minor Tab under the Space/Time Major Tab is the Volume Tab (see Figure 3.1-4). This example shows the conversion of Acre-Foot to Liter. In this example, the amplitude of Acre-Foot is set equal to one (1.0). The conversion equation is shown in Example 3.1-4.

FIGURE 3.1-4 Unit Converter Using MATLAB App - Space/Time Volume Tab.
Acre-Foot (aft) (=1.0) to Liter (L) Example 3.1-4:
L | = | aft * m3/aft * L/m3 = aft * 1.233489E3 * 1 / 1.0E-3 {38} |
= | aft * 1.23348900E6 |
Where: L | = | the number of Liter calculated |
aft | = | the number of Acre-Foot to be converted (1.0) |
m3/aft3 | = | the conversion factor from Acre-Foot to Cubic Meters (1.233489E3) |
L/m3 | = | the conversion factor from Cubic Meters to Liter (1/ 1.0E-3) |
And:
The resulting solution is:
L = 1.0 * 1.23348900E6 = 1.23348900E6 Liter |
(3.1-4) |
The Space/Time Volume Tab allows the bidirectional selection of the following volume dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Volume | ||
| acre-foot (aft) | ||
| barrel-oil (bbl) | ||
| cubic-yard (yd^3) | ||
| cubic-meter (m^3) | ||
| cubic-foot (ft^3) | ||
| board-foot (BF) | ||
| register-ton (RT) | ||
| bushel (bu) | ||
| gallon (gal) | ||
| liter (L) | ||
| quart (qt) | ||
| pint (pt) | ||
| fluid-ounce (fl oz) | ||
| milliliter (mL) | ||
| cubic-inch (in^3) | ||
| cubic-centimeter (cm^3) |
Velocity Tab
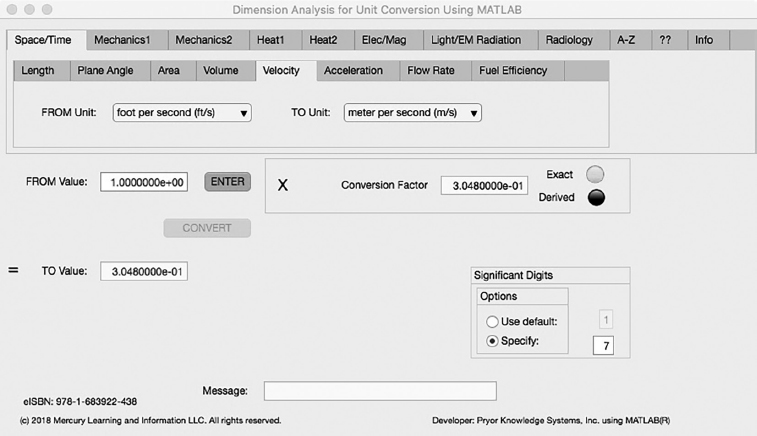
FIGURE 3.1-5 Unit Converter Using MATLAB App - Space/Time Velocity Tab.
The fifth Minor Tab under the Space/Time Major Tab is the Velocity Tab (see Figure 3.1-5). This example shows the conversion of Foot per Second to Meter per Second. In this example, the amplitude of Foot per Second (ft/s) is set equal to one (1.0). The conversion equation is shown in Example 3.1-5.
Foot per Second (ft/s) (=1.0) to Meter per Second (m/s) Example 3.1-5:
m/s = ft/s * m/ft = ft/s * 0.3048
Where: m/s | = | the number of Meter per Second calculated |
ft/s | = | the number of Foot per Second to be converted (1.0) |
m/ft | = | the conversion factor from Foot to Meter (0.3048) |
And:
The resulting solution is:
m/s = 1.0 * 0.3048 = 0.3048 Meter per Second | (3.1-5) |
The Space/Time Velocity Tab allows the bidirectional selection of the following velocity dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Velocity | ||
| foot per second (ft/s) | ||
| mile per hour (mi/hr) | ||
| knot (nmi/hr) | ||
| meter per second (m/s) | ||
| kilometer per hour (km/hr) |
Acceleration Tab
The sixth Minor Tab under the Space/Time Major Tab is the Acceleration Tab (see Figure 3.1-6). This example shows the conversion of Foot per Second Squared to Meter per Second Squared. In this example, the amplitude of Foot per Second Squared (ft/s2) is set equal to one (1.0). The conversion equation is shown in Example 3.1-6.
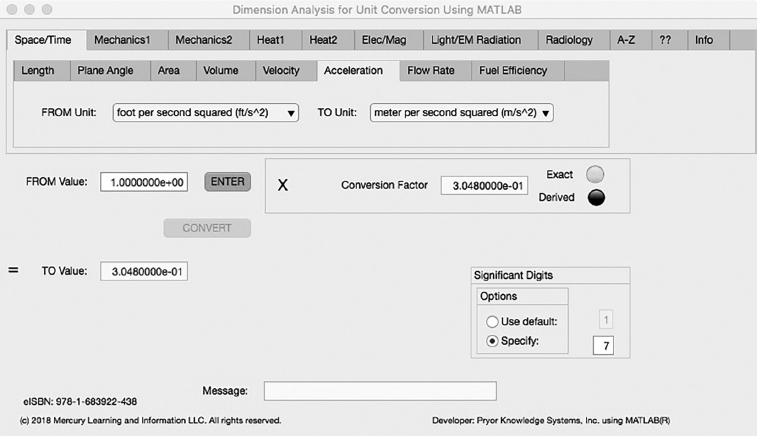
FIGURE 3.1-6 Unit Converter Using MATLAB App - Space/Time Acceleration Tab.
Foot per Second Squared (ft/s2) (=1.0) to Meter per Second Squared (m/s2) Example 3.1-6:
m/s2 = ft/s2 * m/ft = ft/s2 * 0.3048
Where: m/s2 | = | the number of Meter per Second Squared calculated |
ft/s2 | = | the number of Foot per Second Squared to be converted (1.0) |
m/ft | = | the conversion factor from Foot to Meter (0.3048) |
And:
The resulting solution is:
m/s2 = 1.0 * 0.3048 = 0.3048 Meter per Second Squared | (3.1-6) |
The Space/Time Acceleration Tab allows the bidirectional selection of the following acceleration dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Acceleration | ||
| inch per second squared (in/s^2) | ||
| foot per second squared (ft/s^2) | ||
| meter per second squared (m/s^2) | ||
| standard acceleration of gravity (g) |
Flow Rate Tab
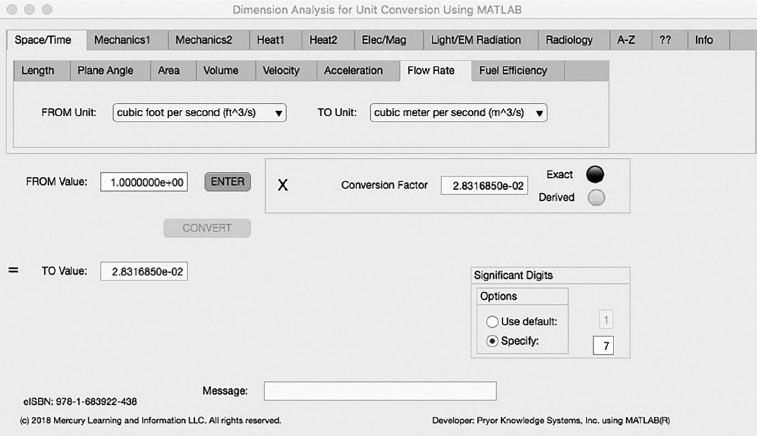
FIGURE 3.1-7 Unit Converter Using MATLAB App - Space/Time Flow Rate Tab.
The seventh Minor Tab under the Space/Time Major Tab is the Flow Rate Tab (see Figure 3.1-7). This example shows the conversion of Cubic Foot per Second to Cubic Meter per Second. In this example, the amplitude of Cubic Foot per Second (ft3/s) is set equal to one (1.0). The conversion equation is shown in Example 3.1-7.
Cubic Foot per Second (ft3/s) (=1.0) to Cubic Meter per Second (m3/s) Example 3.1-7:
m3/s = ft3/s * m3/ft3 = ft3/s * 2.831685E-2
Where: m3/s | = | the number of Cubic Meter per Second calculated |
ft3/s | = | the number of Cubic Foot per Second to be converted (1.0) |
m3/ft3 | = | the conversion factor from Cubic Foot to Cubic Meter (2.831685E-2) |
And:
The resulting solution is:
m3/s = 1.0 * 2.831685E-2 = 2.831685E-2 cubic meter per second | (3.1-7) |
The Space/Time Flow Rate Tab allows the bidirectional selection of the following flow rate dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Flow Rate | ||
| cubic foot per second (ft^3/s) | ||
| cubic foot per minute (ft^3/min) | ||
| cubic yard per minute (yd^3/min) | ||
| gallon per minute (gal/min) | ||
| gallon per day (gal/day) | ||
| cubic meter per second (m^3/s) | ||
| liter per second (L/s) | ||
| liter per day (L/day) |
Fuel Efficiency Tab
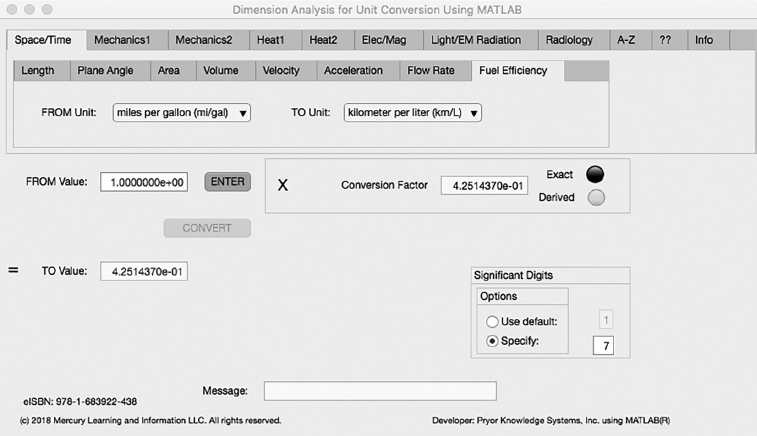
FIGURE 3.1-8 Unit Converter Using MATLAB App - Space/Time Fuel Efficiency Tab.
The eighth Minor Tab under the Space/Time Major Tab is the Fuel Efficiency Tab (see Figure 3.1-8). This example shows the conversion of Mile per Gallon to Kilometer per Liter. In this example, the amplitude of Mile per Gallon (mi/gal) is set equal to one (1.0). The conversion equation is shown in Example 3.1-8.
Mile per Gallon (mi/gal) (=1.0) to Kilometer per Liter (km/L) Example 3.1-8:
km/L | = | mi/gal * km/mi * gal/L = mi/gal * 1.609344 * 1/3.785412 |
= | mi/gal * 4.251437E-1 |
Where: km/L | = | the number of Kilometer per Liter calculated |
mi/gal | = | the number of Mile per Gallon to be converted (1.0) |
km/mi | = | the conversion factor from Miles to Kilometers (1.609344) |
gal/L | = | the conversion factor from Liter to Gallon (1/3.785412) |
And:
The resulting solution is:
km/L = 1.0 * 4.251437E-1 = 4.251437E-1 Kilometer per Liter | (3.1-8) |
The Space/Time Fuel Efficiency Tab allows the bidirectional selection of the following fuel efficiency dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Space/Time | ||
| Fuel Efficiency | ||
| miles per gallon (mi/gal) | ||
| kilometer per liter (km/L) |
3.2 QUANTITIES OF MECHANICS1
FIGURE 3.2-0 Unit Converter Using MATLAB App - Front Panel Mechanics1 Tab.
Figure 3.2-0 shows the Unit Converter MATLAB App Front Panel with the Mechanics1 Major Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Mechanics1 Minor Tabs available in the App is explored herein.
Mass/Weight Tab
The first Minor Tab under the Mechanics1 Major Tab is the Mass/Weight Tab (see Figure 3.2-1). This example demonstrates the conversion of ton (long) (2240 lb) to ounce (avoirdupois). In this example, the amplitude of ton (long) is set equal to one (1.0). The conversion equation is shown in Example 3.2-1.
ton (long) (2240 lb) (=1.0) to ounce (avoirdupois) (oz) Example 3.2-1:
oz | = | ton(long) * lb/ton(long) * oz/lb = 1.0 * 2240 * 16 |
= | ton (long) * 3.584E4 |
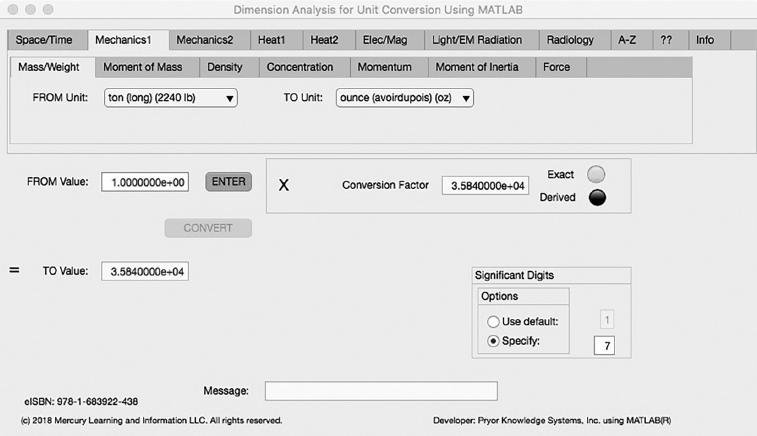
FIGURE 3.2-1 Unit Converter Using MATLAB App - Mechanics1 Mass/Weight Tab.
Where: oz | = | the number of ounces calculated |
ton (long) | = | the number of tons to be converted (1.0) |
lb/ton (long) | = | the conversion factor from ton (long) to pounds (2240) |
oz/lb | = | the conversion factor from pounds to ounces (16) |
And:
The resulting solution is:
oz = ton (long) * 3.584E4 = 3.584E4 ounces | (3.2-1) |
The Mechanics1 Mass/Weight Tab allows the bidirectional selection of the following mass/weight dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics1 | ||
| Mass/Weight | ||
| ton (long) (2240 lb) | ||
| metric ton (t) | ||
| ton (short) (2000 lb) | ||
| slug | ||
| kilogram (kg) | ||
| pound (avoirdupois) | ||
| ounce (troy) | ||
| ounce (avoirdupois) | ||
| gram (g) | ||
| grain | ||
| milligram (mg) |
Moment of Mass Tab
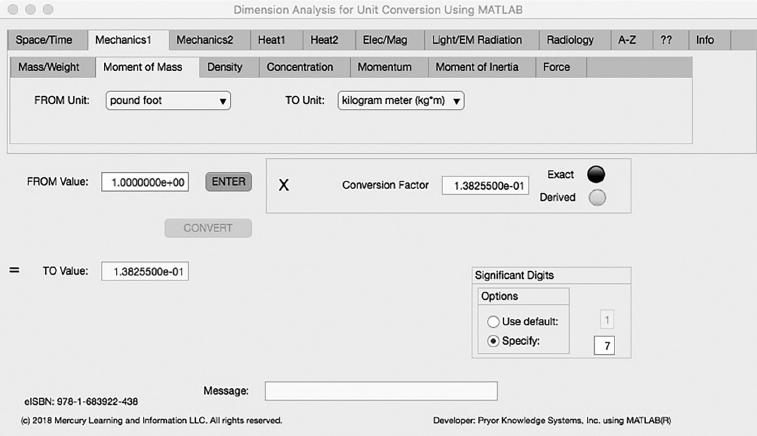
FIGURE 3.2-2 Unit Converter Using MATLAB App - Mechanics1 Moment of Mass Tab.
The second Minor Tab under the Mechanics1 Major Tab is the Moment of Mass Tab (see Figure 3.2-2). This example demonstrates the conversion of pound foot to kilogram meter. In this example, the amplitude of pound foot (lb*ft) is set equal to one (1.0). The conversion equation is shown in Example 3.2-2.
pound foot (lb*ft) (=1.0) to kilogram meter (kg*m) Example 3.2-2:
kg*m | = | lb*ft * kg/lb * m/ft = 1.0 * 0.45359252 * 0.3048 |
= | lb*ft * 1.38255E-1 |
Where: kg*m | = | the number of kilogram meter calculated |
lb*ft | = | the number of pound foot to be converted (1.0) |
kg/lb | = | the conversion factor from pound to kilogram (0.45359252) |
m/ft | = | the conversion factor from foot to meter (0.3048) |
And:
The resulting solution is:
kg*m = 1.0 * 1.38255E-1 = 1.38255E-1 kilogram meter | (3.2-2) |
The Mechanics1 Moment of Mass Tab allows the bidirectional selection of the following Moment of Mass dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics1 | ||
| Moment of Mass | ||
| pound foot | ||
| kilogram meter (kg * m) |
Density Tab
The third Minor Tab under the Mechanics1 Major Tab is the Density Tab (see Figure 3.2-3). This example demonstrates the conversion of pound per cubic foot to kilogram per cubic meter. In this example, the amplitude of pound per cubic foot (lb/ft^3) is set equal to one (1.0). The conversion equation is shown in Example 3.2-3.
pound per cubic foot (lb/ft^3) (=1.0) to kilogram per cubic meter (kg/m^3) Example 3.2-3:
| kg/m^3 | = | lb/ft^3 * kg/lb * ft^3/m^3 = 1.0 * 0.45359252 * 3.5314662E1 |
= | lb/ft^3 * 1.601846E1 |
Where: kg/m^3 | = | the number of kilogram per cubic meter calculated |
lb/ft^3 | = | the number of pound per cubic foot to be converted (1.0) |
kg/lb | = | the conversion factor from pound to kilogram (0.45359252) |
ft^3/m^3 | = | the conversion factor from cubic meter to cubic foot (3.5314662E1) |
And:
The resulting solution is:
kg/m^3 = lb/ft^3 * 1.601846E1= 1.601846E1 kilogram per cubic meter | (3.2-3) |
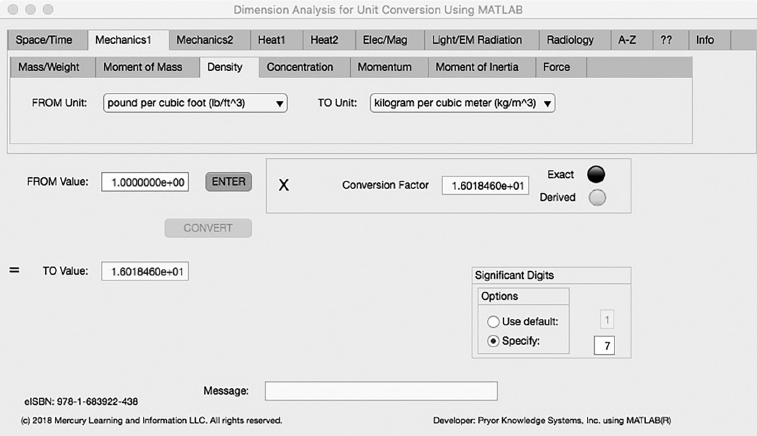
FIGURE 3.2-3 Unit Converter Using MATLAB App - Mechanics1 Density Tab.
The Mechanics1 Density Tab allows the bidirectional selection of the following Density dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics1 | ||
| Density | ||
| ton (2000 lb [short]) per cubic yard | ||
| metric ton per cubic meter (t/m^2) | ||
| pound per cubic foot (lb/ft^3) | ||
| kilogram per cubic meter (kg/m^3) |
Concentration Tab
The fourth Minor Tab under the Mechanics1 Major Tab is the Concentration Tab (see Figure 3.2-4). This example demonstrates the conversion of pound per gallon to gram per liter. In this example, the amplitude of pound per gallon (lb/gal) is set equal to one (1.0). The conversion equation is shown in Example 3.2-4.
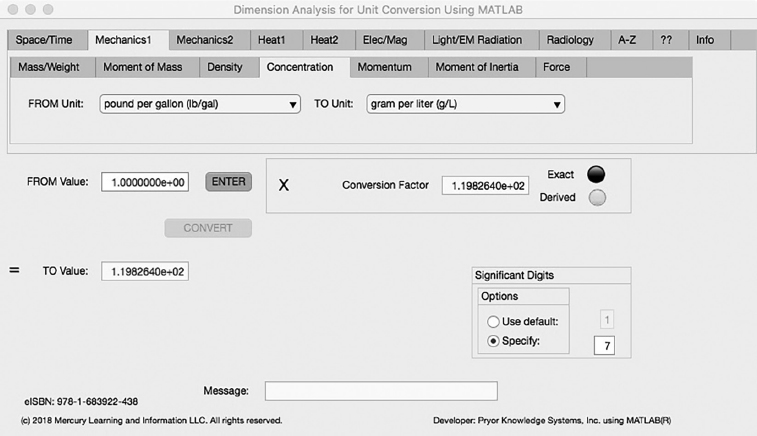
FIGURE 3.2-4 Unit Converter Using MATLAB App - Mechanics1 Concentration Tab.
pound per gallon (lb/gal) (=1.0) to gram per liter (g/L) Example 3.2-4:
g/L | = | lb/gal * kg/lb * g/kg * gal/L |
= | 1.0 * 0.45359237 * 1.0E3 * 1/ 3.785412 | |
= | lb/gal * 1.1982642E2 |
Where: g/L | = | the number of gram per liter calculated |
lb/gal | = | the number of pound per gallon to be converted (1.0) |
kg/lb | = | the conversion factor from pound to kilogram (0.45359252) |
g/kg | = | the conversion factor from kilogram to gram (1.0E3) |
gal/L | = | the conversion factor from liter to gallon (1/ 3.785412) |
And:
The resulting solution is:
g/L = lb/gal * 1.1982642E2= 1.1982642E2 gram per liter | (3.2-4) |
The Mechanics1 Concentration Tab allows the bidirectional selection of the following Concentration dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics1 | ||
| Concentration (mass) | ||
| pound per gallon (lb/gal) | ||
| ounce (avoirdupois) per gallon (oz/gal) | ||
| gram per liter (g/L) |
Momentum Tab
The fifth Minor Tab under the Mechanics1 Major Tab is the Momentum Tab (see Figure 3.2-5). This example demonstrates the conversion of pound foot per second to kilogram meter per second. In this example, the amplitude of pound foot per second (lb*ft/s) is set equal to one (1.0). The conversion equation is shown in Example 3.2-5.
pound foot per second (lb*ft/s) (=1.0) to kilogram meter per second (kg*m/s) Example 3.2-5:
| kg*m/s | = | lb*ft/s * kg/lb * m/ft = lb*ft/s * 4.5359252E-1 * 3.048E-1 |
= | lb*ft/s * 1.38255E-1 |
Where: kg*m/s | = | the number of kilogram meter per second calculated |
lb*ft/s | = | the number of pound foot per second to be converted (1.0) |
kg/lb | = | the conversion factor from pound to kilogram (4.5359252E-1) |
m/ft | = | the conversion factor from foot to meter (3.048E-1) |
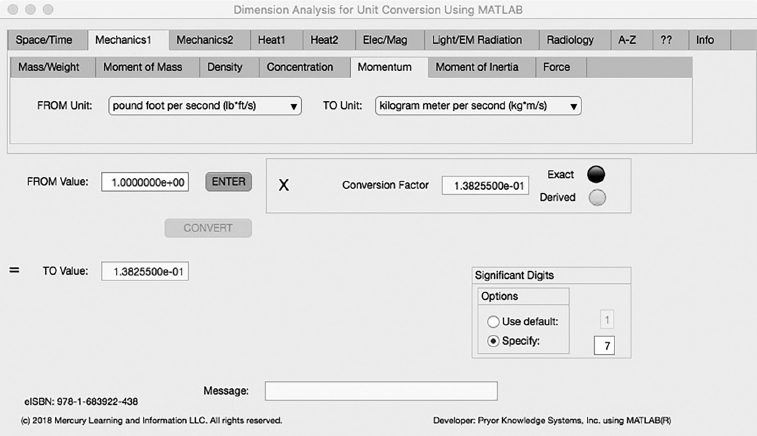
FIGURE 3.2-5 Unit Converter Using MATLAB App - Mechanics1 Momentum Tab.
And:
The resulting solution is:
kg*m/s = lb*ft/s * 1.38255E-1 = 1.38255E-1 kilogram meter per second | (3.2-5) |
The Mechanics1 Momentum Tab allows the bidirectional selection of the following Momentum dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics1 | ||
| Momentum | ||
| pound foot per second (lb*ft/s) | ||
| kilogram meter per second (kg*m/s) |
Moment of Inertia Tab
The sixth Minor Tab under the Mechanics1 Major Tab is the Moment of Inertia Tab (see Figure 3.2-6). This example demonstrates the conversion of pound square foot to kilogram square meter. In this example, the amplitude of pound square foot (lb*ft^2) is set equal to one (1.0). The conversion equation is shown in Example 3.2-6.
pound square foot (lb*ft^2) (=1.0) to kilogram square meter (kg*m^2) Example 3.2-6:
kg*m^2 | = | lb*ft^2 * kg/lb * m^2/ft^2 |
= | lb*ft^2 * 4.5359252E-1 * 9.290300E-2 | |
= | lb*ft^2 * 4.2140110E-2 |
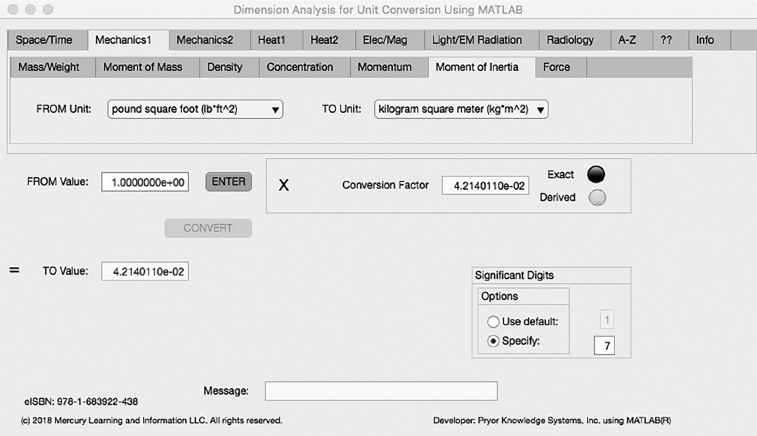
FIGURE 3.2-6 Unit Converter Using MATLAB App - Mechanics1 Moment of Inertia Tab.
Where: kg*m^2 | = | the number of kilogram meter squared calculated |
lb*ft^2 | = | the number of pound foot squared to be converted (1.0) |
kg/lb | = | the conversion factor from pound to kilogram (4.5359252E-1) |
m^2/ft^2 | = | the conversion factor from foot squared to meter squared (9.290300E-2) |
And:
The resulting solution is:
kg*m^2 = 1.0 * 4.2140110E-2 = 4.2140110E-2 kilogram meter squared |
(3.2-6) |
The Mechanics1 Moment of Inertia Tab allows the bidirectional selection of the following Moment of Inertia dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics1 | ||
| Moment of Inertia | ||
| pound square foot (lb*ft^2) | ||
| kilogram square meter (kg*m^2) |
Force Tab
The seventh Minor Tab under the Mechanics1 Major Tab is the Force Tab (see Figure 3.2-7). This example demonstrates the conversion of pound-force to Newton (N). In this example, the amplitude of pound-force (lbf) is set equal to one (1.0). The conversion equation is shown in Example 3.2-7.
pound-force (lbf) (=1.0) to Newton (N) Example 3.2-7:
N | = | lbf * kg/lb * gn |
= | lbf * 4.5359237E-1 * 9.80665 | |
= | lbf * 4.4482216E0 |
Where: N | = | the number of Newton calculated |
lbf | = | the number of pound-force being converted (1.0) |
kg/lb | = | the conversion factor from pound to kilogram (4.5359237E-1) |
gn | = | the gravitational acceleration at the surface of the earth (9.80665) |
And:
The resulting solution is:
N = 1.0 * 4.4482216E0 Newton |
(3.2-7) |
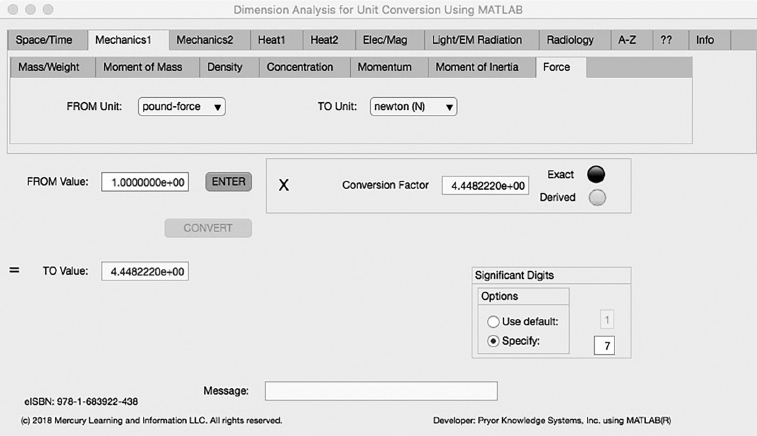
FIGURE 3.2-7 Unit Converter Using MATLAB App - Mechanics1 Force Tab.
The Mechanics1 Force Tab allows the bidirectional selection of the following Force dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics1 | ||
| Force | ||
| pound-force | ||
| poundal | ||
| newton (N) |
3.3 QUANTITIES OF MECHANICS2
FIGURE 3.3-0 Unit Converter Using MATLAB App - Front Panel Mechanics2 Tab.
Figure 3.3-0 shows the Unit Converter MATLAB App Front Panel with the Mechanics2 Major Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Mechanics2 Minor Tabs available in the App is explored herein.
Moment of Force, Torque Tab
The first Minor Tab under the Mechanics2 Major Tab is the Moment of Force, Torque Tab (see Figure 3.3-1). This example demonstrates the conversion of pound-force foot (lbf*ft) to Newton meter (N*m). In this example, the amplitude of pound-force foot (lbf*ft) is set equal to one (1.0). The conversion equation is shown in Example 3.3-1.
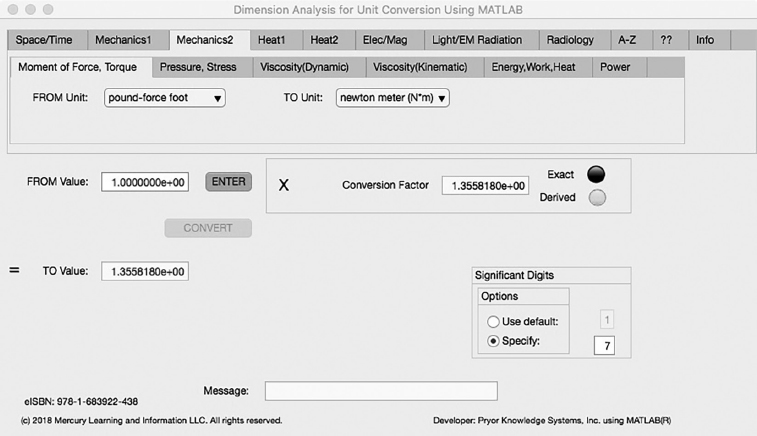
FIGURE 3.3-1 Unit Converter Using MATLAB App - Mechanics2 Moment of Force, Torque Tab.
pound-force (lbf) * foot (ft) (=1.0) to Newton (N) * meter (m) Example 3.3-1:
N*m | = | lbf * kg/lb * gn *ft |
= | lbf * 4.5359237E-1 * 9.80665 * 0.3048 | |
= | lbf * ft * 1.355818E0 |
Where: N * m | = | the number of Newton meter calculated |
lbf * ft | = | the number of pound-force foot being converted (1.0) |
kg/lb | = | the conversion factor from pound to kilogram (4.5359237E-1) |
gn | = | the gravitational acceleration at the surface of the earth (9.80665) |
m/ft | = | the conversion factor from foot to meter (0.3048) |
And:
The resulting solution is:
N*m = 1.0 * 1.355818E0 = 1.355818E0 Newton-meter | (3.3-1) |
The Mechanics2 Moment of Force, Torque Tab allows the bidirectional selection of the following Moment of Force, Torque dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics2 | ||
| Moment of Force, Torque | ||
| pound-force foot | ||
| pound-force inch | ||
| newton meter (N*m) |
Pressure, Stress Tab
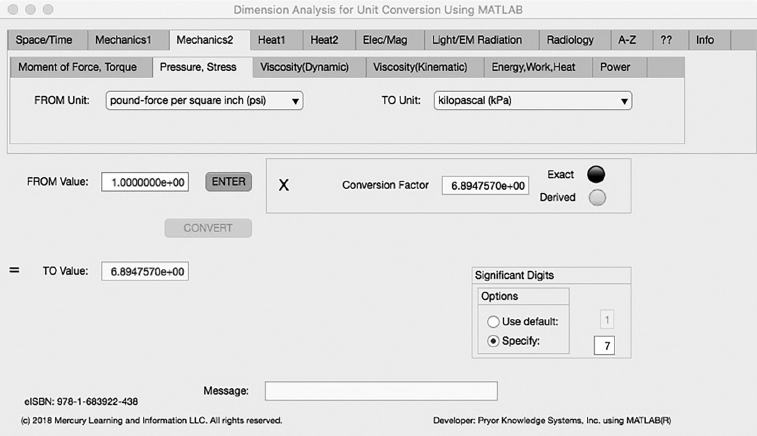
FIGURE 3.3-2 Unit Converter Using MATLAB App - Mechanics2 Pressure, Stress Tab.
The second Minor Tab under the Mechanics2 Major Tab is the Pressure, Stress Tab (see Figure 3.3-2). This example demonstrates the conversion of pound-force per square inch to kilopascal. In this example, the amplitude of pound-force per square inch (psi) (lbf/in^2) is set equal to one (1.0). The conversion equation is shown in Example 3.3-2.
pound-force per square inch (psi) (=1.0) to kilopascal (kPa) Example 3.3-2:
kPa | = | lbf/in^2* in^2/m^2 * N/lbf * kPa/Pa |
= | lbf/in^2* 1.550031E3 * 4.448222E0 * 1.0E-3 | |
= | lbf/in^2* 6.894757E0 |
Where: kPa | = | the number of kilopascal calculated |
lbf/in^2 (psi) | = | the number of lbf/in^2 (psi) to be converted (1.0) |
in^2/m^2 | = | the conversion factor from m^2 to in^2 (1.550031E3) |
N/lbf | = | the conversion factor from lbf to N (4.448222E0) |
kPa/Pa | = | the conversion factor from Pa to kPa (1.0E-3) |
And:
The resulting solution is:
kPa = lbf/in^2* 6.894757E0= 6.894757E0 kilopascal | (3.3-2) |
The Mechanics2 Pressure, Stress Tab allows the bidirectional selection of the following Pressure, Stress dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics2 | ||
| Pressure, Stress | ||
| megapascal (Mpa) | ||
| standard atmosphere | ||
| bar | ||
| kilopascal (kPa) | ||
| millibar | ||
| pound-force per square inch (psi) | ||
| kilopound-force per square inch | ||
| pound-force per square foot | ||
| inch of mercury (32 degF) | ||
| foot of water (39.2 degF) | ||
| inch of water (39.2 degF) | ||
| millimeter of mercury (32 degF) | ||
| torr (Torr) | ||
| pascal (Pa) |
Viscosity (Dynamic) Tab
The third Minor Tab under the Mechanics2 Major Tab is the Viscosity (Dynamic) Tab (see Figure 3.3-3). This example demonstrates the conversion of centipoise to millipascal second. In this example, the amplitude of centipoise (cP) is set equal to one (1.0). The conversion equation is shown in Example 3.3-3.
centipoise (cP) (=1.0) to millipascal second (mPa*s) Example 3.3-3:
mPa*s = cP * mPa*s/cP = 1.0 * 1.0 = cP * 1.0
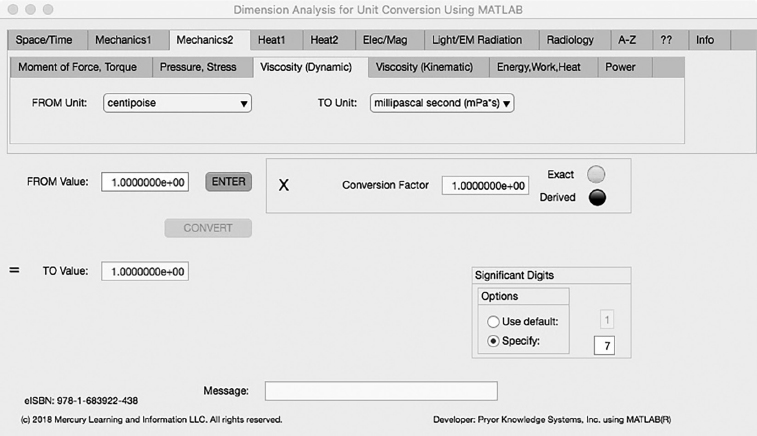
FIGURE 3.3-3 Unit Converter Using MATLAB App - Mechanics2 Viscosity (Dynamic) Tab.
Where: mPa*s | = | the number of millipascal calculated |
cP | = | the number of centipoise to be converted (1.0) |
mPa*s/cP | = | the conversion factor from centipoise to millipascal*second (1.0) |
And:
The resulting solution is:
mPa*s = cP * mPa*s/cP = 1.0 * 1.0 = 1.0 millipascal second | (3.3-3) |
The Mechanics2 Viscosity (Dynamic) Tab allows the bidirectional selection of the following Viscosity (Dynamic) dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics2 | ||
| Viscosity (Dynamic) | ||
| centipoise | ||
| millipascal second (mPa*s) |
Viscosity (Kinematic) Tab
The fourth Minor Tab under the Mechanics2 Major Tab is the Viscosity (Kinematic) Tab (see Figure 3.3-4). This example demonstrates the conversion of centistokes to square millimeter per second. In this example, the amplitude of centistokes (cSt) is set equal to one (1.0). The conversion equation is shown in Example 3.3-4.
centistokes (cSt) (=1.0) to square millimeter per second (mm^2/s) Example 3.3-4:
mm^2/s = cSt * (mm^2/s)/cSt = 1.0 * 1.0 = cSt * 1.0
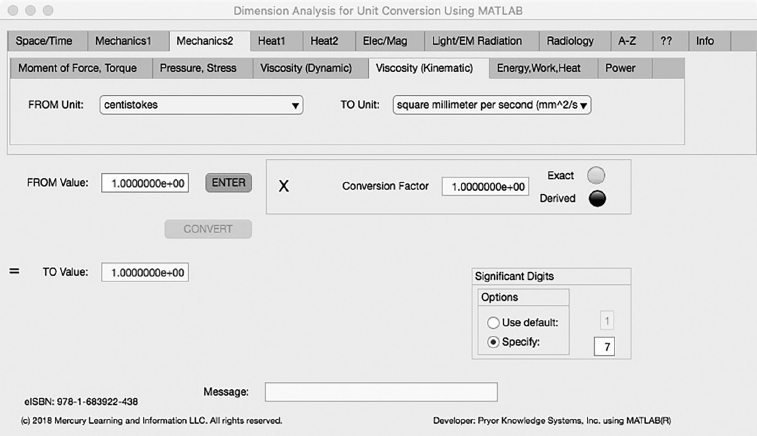
FIGURE 3.3-4 Unit Converter Using MATLAB App - Mechanics2 Viscosity (Kinematic) Tab.
Where: mm^2/s | = | the number of millimeter squared per second calculated |
cSt | = | the number of centistoke to be converted (1.0) |
(mm^2/s)/cSt | = | the conversion factor from centistoke to mm^2 per second (1.0) |
And:
The resulting solution is:
mm^2/s = cSt * (mm^2/s)/cSt = 1.0 * 1.0 = 1.0 millimeter squared per second | (3.3-4) |
The Mechanics2 Viscosity (Kinematic) Tab allows the bidirectional selection of the following Viscosity (Kinematic) dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics2 | ||
| Viscosity (Kinematic) | ||
| centistokes | ||
| square millimeter per second (mm^2/s) |
Energy, Work, Heat Tab
The fifth Minor Tab under the Mechanics2 Major Tab is the Energy, Work, Heat Tab (see Figure 3.3-5). This example demonstrates the conversion of kilowatthour to joule. In this example, the amplitude of kilowatthour (kW * h) is set equal to one (1.0). The conversion equation is shown in Example 3.3-5.
kilowatthour (kW * h) (=1.0) to joule (J) Example 3.3-5:
J | = | kW * h * W/kW * min/h * s/min |
= | kW * h * 1.0E3 * 6.0E1 * 6.0E1 | |
= | kW * h * 3.6E6 |
Where: J | = | the number of joule calculated |
kW * h | = | the number of kilowatthour to be converted (1.0) |
W/kW | = | the conversion factor from kilowatt to watt (1.0E3) |
min/h | = | the conversion factor from hour to minute (6.0E1) |
s/min | = | the conversion factor from minute to second (6.0E1) |
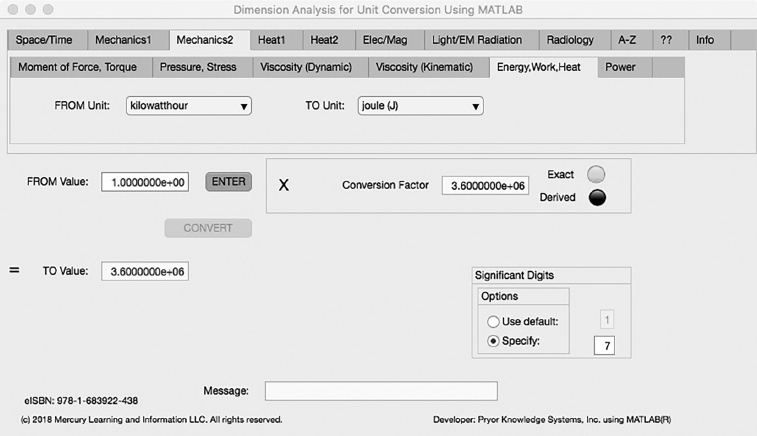
FIGURE 3.3-5 Unit Converter Using MATLAB App - Mechanics2 Energy, Work, Heat Tab.
And:
The resulting solution is:
J = 1.0 * 3.6E6 = 3.6E6 joule per kilowatthour | (3.3-5) |
The Mechanics2 Energy, Work, Heat Tab allows the bidirectional selection of the following Energy, Work, Heat dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics2 | ||
| Energy, Work, Heat | ||
| kilowatthour | ||
| megajoule (MJ) | ||
| calorie (physics) | ||
| kilojoule (kJ) | ||
| calorie (nutrition) (kCal) | ||
| joule (J) | ||
| Btu | ||
| therm (U.S.) | ||
| horsepower hour | ||
| foot pound-force |
Power Tab
The sixth Minor Tab under the Mechanics2 Major Tab is the Power Tab (see Figure 3.3-6). This example demonstrates the conversion of Btu per second to Btu per hour. In this example, the amplitude of Btu per second (Btu/s) is set equal to one (1.0). The conversion equation is shown in Example 3.3-6.
Btu per second (Btu/s) (=1.0) to Btu per hour (Btu/h) 3.3-6:
Btu/h | = | Btu/s * s/min * min/h |
= | Btu/s * 6.0E1 * 6.0E1 | |
= | Btu/s * 3.6E3 |
Where: Btu/h | = | the number of Btu/h calculated |
Btu/s | = | the number of Btu/s to be converted (1.0) |
min/h | = | the conversion factor from hour to minute (6.0E1) |
s/min | = | the conversion factor from minute to second (6.0E1) |
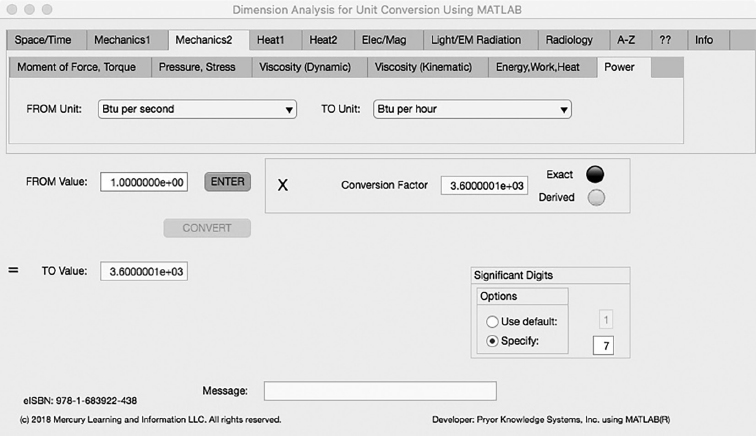
FIGURE 3.3-6 Unit Converter Using MATLAB App - Mechanics2 Power Tab.
And:
The resulting solution is:
Btu/h = 1.0 * 3.6E3 = 3.6E3 Btu per hour | (3.3-6) |
The Mechanics2 Power Tab allows the bidirectional selection of the following Power dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Mechanics2 | ||
| Power | ||
| ton, refrigeration (12 000 Btu/h) | ||
| kilowatt (kW) | ||
| Btu per second | ||
| Btu per hour | ||
| watt (W) | ||
| horsepower (550 ft-lbF/s) | ||
| horsepower, electric | ||
| foot pound-force per second (ft-lbF/s) |
3.4 QUANTITIES OF HEAT1
FIGURE 3.4-0 Unit Converter Using MATLAB App - Front Panel Heat1 Tab.
Figure 3.4-0 shows the Unit Converter MATLAB App Front Panel with the Heat1 Major Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Heat1 Minor Tabs available in the App is explored herein.
Temperature Tab
The first Minor Tab under the Heat1 Major Tab is the Temperature Tab (see Figure 3.4-1). This example demonstrates the conversion of Fahrenheit to Celsius. In this example, the amplitude of Fahrenheit (°F) is set equal to fifty (50). The conversion equation is shown in Example 3.4-1.
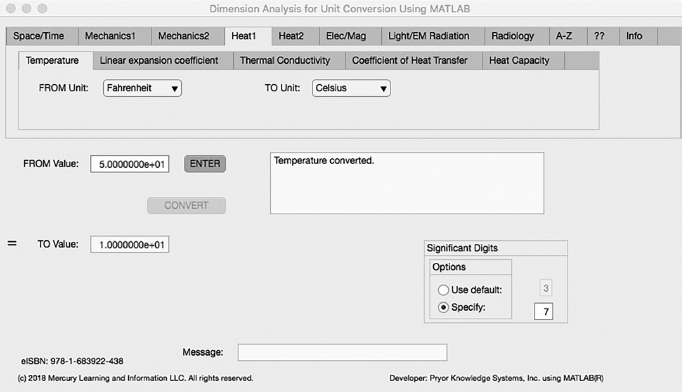
FIGURE 3.4-1 Unit Converter Using MATLAB App - Heat1 Temperature Tab.
Temperature (°F) (= 50.0) to Temperature (°C) Example 3.4-1:
°C = (°F-32)/1.8 = (50.0-32.0)/1.8 = 18.0/1.8 = 10
Where: °C | = | the Celsius temperature calculated |
°F | = | the Fahrenheit temperature being converted (50.0) |
(°F-32)/1.8 | = | the conversion formula from Fahrenheit to Celsius |
And:
The resulting solution is:
°F (50.0) = °C (10.0) | (3.4-1) |
The Heat1 Temperature Tab allows the bidirectional selection of the following Temperature dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat1 | ||
| Temperature | ||
| Fahrenheit | ||
| Celsius | ||
| Kelvin |
Linear Expansion coefficient Tab
The second Minor Tab under the Heat1 Major Tab is the Linear Expansion coefficient Tab (see Figure 3.4-2). This example demonstrates the conversion of reciprocal Fahrenheit (°F) to reciprocal Celsius (°C). In this example, the amplitude of Fahrenheit (°F) is set equal to eighteen (18). The conversion equation is shown in Example 3.4-2.
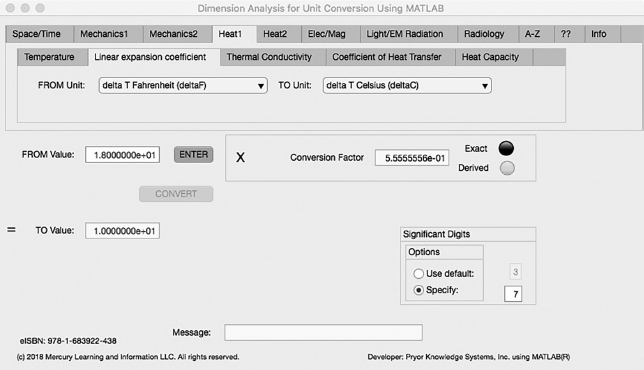
FIGURE 3.4-2 Unit Converter Using MATLAB App - Heat1 Linear Expansion coefficient Tab.
Temperature (°F) (=18.0) to Temperature (°C) Example 3.4-2:
| delta (1/°C) | = | delta (1/°F)*1.8 = delta (1.8/18) = 0.1 |
delta (°C) | = | 1/0.1 = 10 |
Where: delta °C = the differential Celsius temperature calculated delta °F = the differential Fahrenheit temperature being converted (18.0)
And:
The resulting solution is:
delta °F (18.0) = delta °C (10.0) | (3.4-2) |
The Heat1 Linear Expansion coefficient Tab allows the bidirectional selection of the following Linear Expansion coefficient dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat1 | ||
| Linear expansion coefficient | ||
| delta T Fahrenheit (delta °F) | ||
| delta T kelvin (delta K) | ||
| delta T Celsius (delta °C) |
Thermal Conductivity Tab
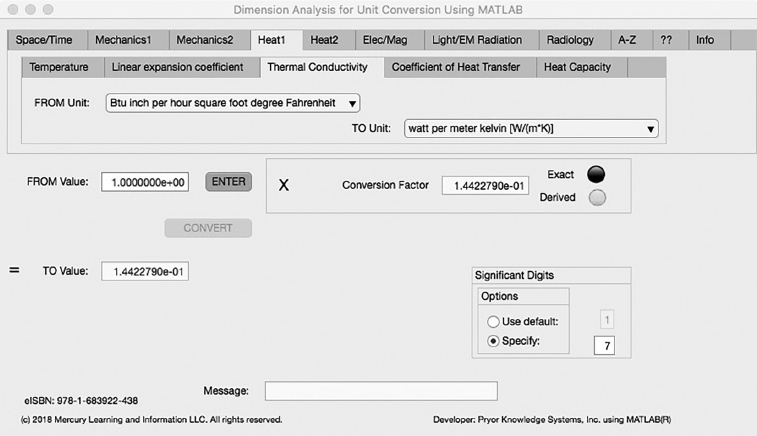
FIGURE 3.4-3 Unit Converter Using MATLAB App - Heat1 Thermal Conductivity Tab.
The third Minor Tab under the Heat1 Major Tab is the Thermal Conductivity Tab (see Figure 3.4-3). This example demonstrates the conversion of Btu inch per hour square foot degree Fahrenheit to watt per meter kelvin. In this example, the amplitude of Btu inch per hour square foot degree Fahrenheit (Btu * in/(h*ft^2*F)) is set equal to one (1.0). The conversion equation is shown in Example 3.4-3.
Btu * in/(h*ft^2*F) (=1.0) to W/(m*K) Example 3.4-3:
| W/(m*K) | = | Btu * in/(h*ft^2*F) * h/min * min/s * m/in * ft^2/m^2 * F/K |
= | 1.0 * 1.055056E3 * 1/60 * 1/60 * 2.54E-2 * 1/9.290304E-2 * 1.8 | ||
= | Btu * in/(h*ft^2*F) * 1.4422791E-1 |
Where: W/(m*K) | = | the SI Thermal Conductivity calculated |
Btu as joules | = | W *s * 1.055056E3 |
Btu * in/(h*ft^2*F) | = | Thermal Conductivity being converted (1.0) |
h/min | = | number of hours per minute (1/60) |
min/s | = | number of minutes per second (1/60) |
m/in | = | number of meter per inch (2.54E-2) |
ft^2/m^2 | = | number of square meter per square foot (1/9.290304E-2) |
F/K | = | number of degree Fahrenheit per degree kelvin (1.8) |
And:
The resulting solution is:
W/(m*K) = 1.0 * 1.4422791E-1 = 1.4422791E-1 watt per meter kelvin | (3.4-3) |
The Heat1 Thermal Conductivity Tab allows the bidirectional selection of the following Thermal Conductivity dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat1 | ||
| Thermal Conductivity | ||
| Btu inch per hour square foot degree Fahrenheit | ||
| watt per meter kelvin [W/(m*K)] |
Coefficient of Heat Transfer Tab
The fourth Minor Tab under the Heat1 Major Tab is the Coefficient of Heat Transfer Tab (see Figure 3.4-4). This example demonstrates the conversion of Btu inch per hour square foot degree Fahrenheit (Btu * in/(h*ft^2*F)) to watt per square meter kelvin (W/(m^2*K)). In this example, the amplitude of Btu inch per hour square foot degree Fahrenheit (Btu * in/(h*ft^2*F)) is set equal to one (1.0). The conversion equation is shown in Example 3.4-4.
Btu * in/(h*ft^2*F) (=1.0) to W/(m^2*K) Example 3.4-4:
| W/(m^2*K) | = | Btu * 1/(h*ft^2*F) * h/min * min/s * ft^2/m^2 * F/K |
= | 1.0 * 1.055056E3 * 1/60 * 1/60 * 1/9.290304E-2 * 1.8 | ||
= | Btu * 1/(h*ft^2*F) * 5.678264E0 |
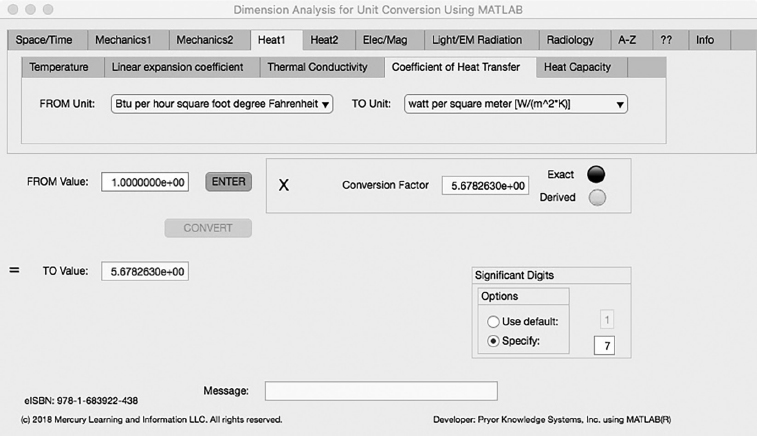
FIGURE 3.4-4 Unit Converter Using MATLAB App - Heat1 Coefficient of Heat Transfer Tab.
Where: W/(m^2*K) | = | the SI Coefficient of Heat Transfer calculated |
Btu as joules | = | W *s * 1.055056E3 |
Btu * 1/(h*ft^2*F) | = | Coefficient of Heat Transfer being converted (1.0) |
h/min | = | number of hours per minute (1/60) |
min/s | = | number of minutes per second (1/60) |
ft^2/m^2 | = | number of square meter per square foot (1/9.290304E-2) |
F/K | = | number of degree Fahrenheit per degree kelvin (1.8) |
And:
The resulting solution is:
W/(m^2*K) = Btu * 1/(h*ft^2*F) * 5.678264E0 = 1.0 * 5.678264E0 = 5.678264E0 watts per square meter | (3.4-4) |
The Heat1 Coefficient of Heat Transfer Tab allows the bidirectional selection of the following Coefficient of Heat Transfer dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat1 | ||
| Coefficient of Heat Transfer | ||
| Btu per hour square foot degree Fahrenheit | ||
| watts per square meter kelvin [W/(m^2*K)] |
Heat Capacity Tab
The fifth Minor Tab under the Heat1 Major Tab is the Heat Capacity Tab (see Figure 3.4-5). This example demonstrates the conversion of Btu per degree Fahrenheit (Btu/ °F) to kilojoule per kelvin (kJ/K). In this example, the amplitude of Btu per degree Fahrenheit (Btu/F)) is set equal to one (1.0). The conversion equation is shown in Example 3.4-5.
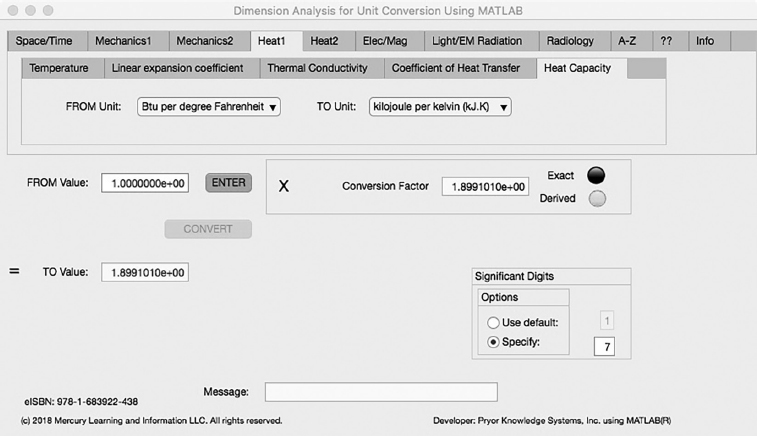
FIGURE 3.4-5 Unit Converter Using MATLAB App - Heat1 Heat Capacity Tab.
Btu/ °F (=1.0) to kJ/K Example 3.4-5:
kJ/K | = | Btu/ °F * kJ/J * °F/K |
= | Btu/ °F * 1.055056E3 * 1.0E-3 * 1.8 | |
= | Btu/ °F * 1.899101E0 |
Where: kJ/K | = | the SI Coefficient of Heat Capacity calculated |
Btu as joules | = | W *s * 1.055056E3 |
Btu/ °F | = | Coefficient of Heat Capacity being converted (1.0) |
°F/K | = | number of degree Fahrenheit per degree kelvin (1.8) |
kJ/J | = | 1.0E-3 |
And:
The resulting solution is:
kJ/K = 1.0 * 1.899101E0 = 1.899101E0 kilojoules per kelvin | (3.4-5) |
The Heat1 Heat Capacity Tab allows the bidirectional selection of the following Heat Capacity dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat1 | ||
| Heat Capacity | ||
| Btu per degree Fahrenheit | ||
| kilojoule per kelvin (kJ/K) |
3.5 QUANTITIES OF HEAT2
FIGURE 3.5-0 Unit Converter Using MATLAB App - Front Panel Heat2 Tab.
Figure 3.5-0 shows the Unit Converter MATLAB App Front Panel with the Heat2 Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Tabs available in the App is explored herein.
Specific Heat Capacity Tab
The first Minor Tab under the Heat2 Major Tab is the Specific heat capacity Tab (see Figure 3.5-1). This example shows the conversion of Btu per pound degree Fahrenheit (Btu/(lb * °F) to Kilojoule per kilogram kelvin [kJ/(kg * K)]. In this example, the amplitude of Btu per pound degree Fahrenheit is set equal to one (1.0). The conversion equation is shown in Example 3.5-1.
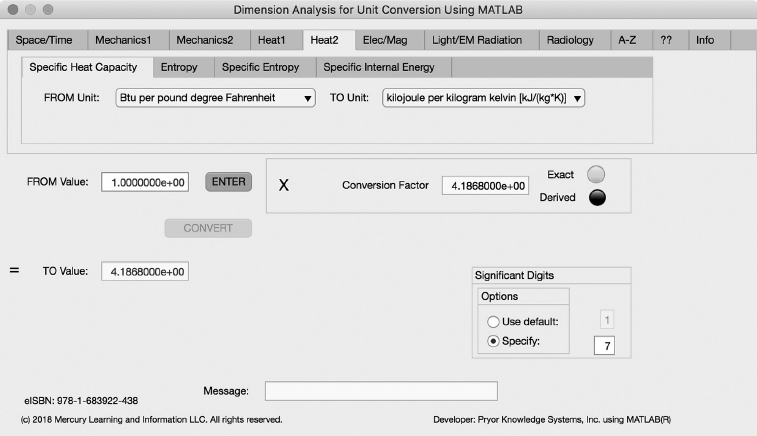
FIGURE 3.5-1 Unit Converter Using MATLAB App - Heat2 Specific Heat Capacity Tab.
Btu/(lb* °F) (=1.0) to kJ/(kg * K) Example 3.5-1:
| kJ/(kg * K) | = | Btu/(lb * °F) * J/Btu * kJ/J * lb/kg * F/K |
= | Btu/(lb* °F) * 1.055056E3 * 1/1000 * 1/4.535924E-1 *1/5.55556E-1 | ||
= | BTU/(lb * F) * 4.1868E0 |
Where: kJ/(kg * K) | = | the number of kilojoule per kilogram kelvin calculated |
Btu/(lb*F) | = | the number of Btu per pound degree Fahrenheit to be converted (1.0) |
J/BTU | = | the conversion factor from Btu to joule (1.055056E3) |
kJ/J | = | the conversion factor from joule to kilojoule (1/1000) |
lb/kg | = | the conversion factor from kilogram to pound (1/4.535924E-1) |
F/K | = | the conversion factor from kelvin degree interval to Fahrenheit degree interval (1/5.55556E-1) |
And:
The resulting solution is:
kJ/(kg * K) = 1.0 * 4.1868E+0 = 4.1868E+0 kilojoule per kilogram kelvin | (3.5-1) |
The Heat2 Specific heat capacity Tab allows the bidirectional selection of the following Specific heat capacity dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat2 | ||
| Specific Heat Capacity | ||
| Btu per pound degree Fahrenheit | ||
| kilojoule per kilogram kelvin (KJ/(kg * K)) |
Entropy Tab
The second Minor Tab under the Heat2 Major Tab is the Entropy Tab (see Figure 3.5-2). This example shows the conversion of Btu per degree Rankine (Btu/R) to kilojoule per kelvin (kJ/K). In this example, the amplitude of Btu per degree Rankine is set equal to one (1.0). The conversion equation is shown in Example 3.5-2.
Btu/R (=1.0) to kJ/K Example 3.5-2:
| kJ/(K) | = | Btu/R * J/Btu * kJ/J * R/K |
= | Btu/R * 1.055056E3 * 1/1000 * 1/5.55556E-1 | ||
= | Btu/R * 1.899101E0 |
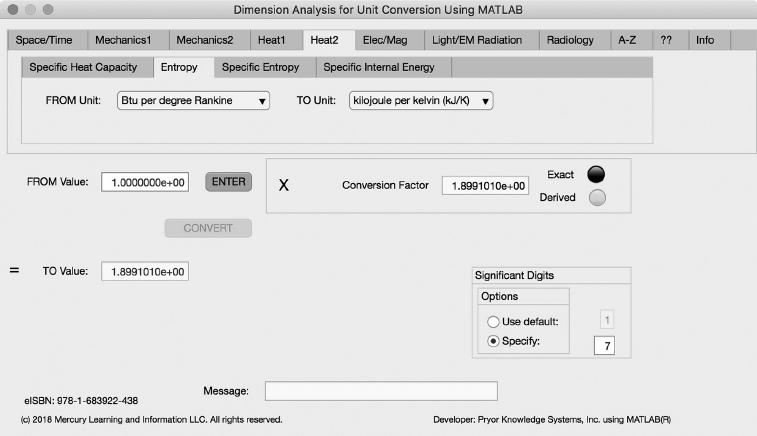
FIGURE 3.5-2 Unit Converter Using MATLAB App - Heat2 Entropy Tab.
Where: kJ/K | = | the number of kilojoule per kelvin calculated |
Btu/R | = | the number of Btu per degree Rankine to be converted (1.0) |
J/Btu | = | the conversion factor from Btu to joule (1.055056E3) |
kJ/J | = | the conversion factor from joule to kilojoule (1/1000) |
R/K | = | the conversion factor from kelvin degree interval to Rankine degree interval (1/5.55556E-1) |
And:
The resulting solution is:
kJ/K = 1.0 * 1.899101E0 = 1.899101E0 kilojoule per kelvin | (3.5-2) |
The Heat2 Entropy Tab allows the bidirectional selection of the following entropy dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat2 | ||
| Entropy | ||
| Btu per degree Rankine (BTU/R) | ||
| kilojoule per kelvin (kJ/K) |
Specific Entropy
The third Minor Tab under the Heat2 Major Tab is the Specific entropy Tab (see Figure 3.5-3). This example shows the conversion of Btu per pound degree Rankine [Btu/(lb*R)] to kilojoule per kilogram kelvin [kJ/(kg*K)]. In this example, the amplitude of Btu per pound degree Rankine [Btu/(lb*R)] is set equal to one (1.0). The conversion equation is shown in Example 3.5-3.
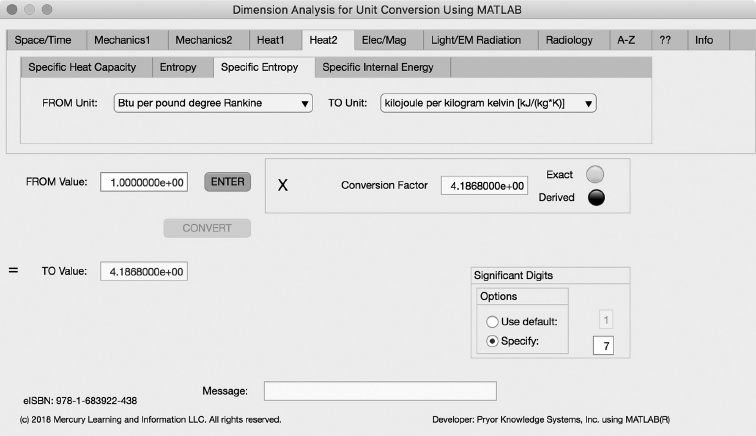
FIGURE 3.5-3 Unit Converter Using MATLAB App - Heat2 Specific Entropy Tab.
Btu/(lb*R) (=1.0) to kJ/(kg*K) Example 3.5-3:
| kJ/(kg*K) | = | Btu/(lb*R)*J/Btu*kJ/J*lb/kg*R/K |
= | Btu/(lb*R)*1.055056E3*1/1000 *1/4.535924E-1*1/5.55556E-1 | ||
= | Btu/(lb*R)*4.1868E0 |
Where: kJ/(kg*K) | = | the number of kilojoule per kilogram kelvin calculated |
Btu/(lb*R) | = | the number of Btu per pound degree Fahrenheit to be converted (1.0) |
J/Btu | = | the conversion factor from Btu to joule (1.055056E3) |
kJ/J | = | the conversion factor from joule to kilojoule (1/1000) |
lb/kg | = | the conversion factor from kilogram to pound (1/4.535924E-1) |
R/K | = | the conversion factor from kelvin degree interval to Fahrenheit degree interval (1/5.55556E-1) |
And:
The resulting solution is:
kJ/(kg*K) = 1.0*4.1868E+0 = 4.1868E+0 kilojoule per kilogram kelvin | (3.5-3) |
The Heat2 Specific Entropy Tab allows the bidirectional selection of the following Specific Entropy dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat2 | ||
| Specific Entropy | ||
| Btu per pound degree Rankine [Btu/(lb * R)] | ||
| kilojoule per kilogram kelvin ([kJ/(kg*K)]) |
Specific Internal Energy Tab
The fourth Minor Tab under the Heat2 Major Tab is the Specific Internal Energy Tab (see Figure 3.5-4). This example shows the conversion of Btu per pound (Btu/lb) to kilojoule per kilogram (kJ/kg). In this example, the amplitude of Btu per pound is set equal to one (1.0). The conversion equation is shown in Example 3.5-4.
Btu per pound to kilojoule per kilogram (kJ/kg) Example 3.5-4:
kJ/kg | = | Btu/lb* J/Btu * kJ/J * lb/kg |
= | Btu/lb * 1.055056E3 * 1/1000 * 1/4.535924E-1 | |
= | Btu/lb * 2.326E0 |
Where: kJ/kg | = | the number of kilojoule per kilogram calculated |
Btu/lb | = | the number of Btu per pound to be converted (1.0) |
J/Btu | = | the conversion factor from Btu to joule (1.055056E3) |
kJ/J | = | the conversion factor from joule to kilojoule (1/1000) |
lb/kg | = | the conversion factor from kilogram to pound (1/4.535924E-1) |
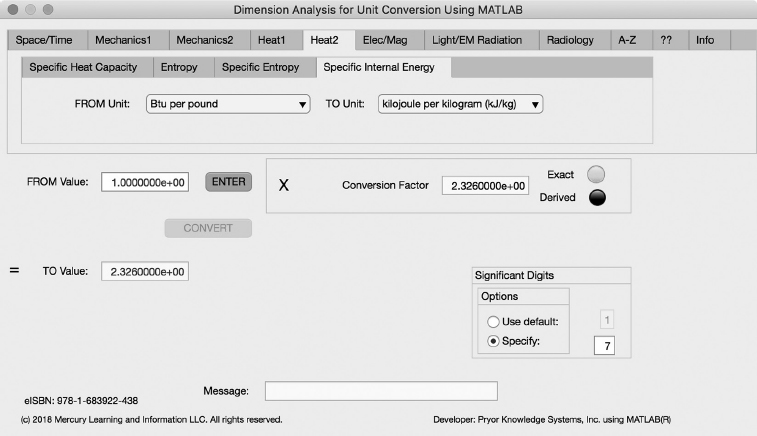
FIGURE 3.5-4 Unit Converter Using MATLAB App - Heat2 Specific Internal Energy Tab.
And:
The resulting solution is:
kJ/kg = 1.0 * 2.326E0 = 2.326E0 kilojoule per kilogram | (3.5-4) |
The Heat2 Specific Internal Energy Tab allows the bidirectional selection of the following specific internal energy dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Heat2 | ||
| Specific Internal Energy | ||
| Btu per pound (Btu/lb) | ||
| kilojoule per kilogram (kJ/kg) |
3.6 QUANTITIES OF ELECTRICITY AND MAGNETISM
FIGURE 3.6-0 Unit Converter Using MATLAB App - Front Panel Elec/Mag Tab.
Figure 3.6-0 shows the Unit Converter MATLAB App Front Panel with the Electricity and Magnetism (ElecMag) Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Tabs available in the App is explored herein.
Magnetic Field Strength Tab
The first Minor Tab under the Elec/Mag Major Tab is the Magnetic Field Strength Tab (see Figure 3.6-1). This example demonstrates the conversion of oersted to ampere/meter (A/m). In this example, the amplitude of oersted is set equal to one (1.0). The conversion equation is shown in Example 3.6-1 {37}.
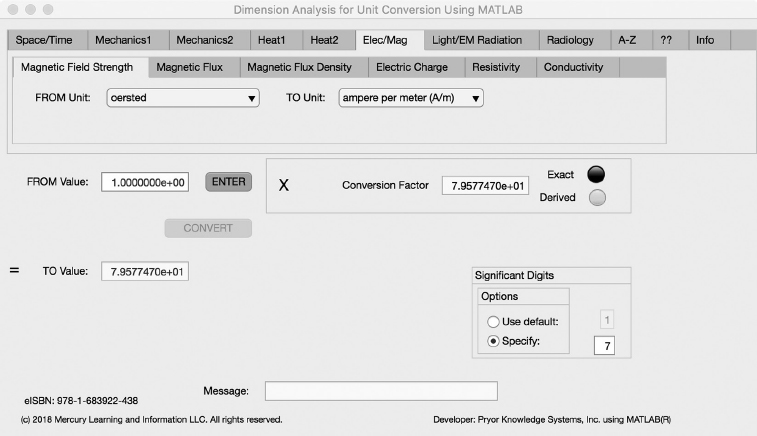
FIGURE 3.6-1 Unit Converter Using MATLAB App - Elec/Mag Magnetic Field Strength Tab.
oersted (=1.0) to ampere/meter (A/m) Example 3.6-1:
A/m = oersted * (A/m)/oersted = 1.0 * 1000/4p = 1.0 * 79.57747
Where: A/m | = | the number of amperes per meter calculated |
oersted | = | the number of oersted to be converted (1.0) |
(A/m)/oersted | = | the conversion factor from oersted to ampere/meter (79.57747) |
And:
The resulting solution is:
A/m = 1.0* 7.957747E+1 = 7.957747E+1 ampere per meter | (3.6-1) |
The Elec/Mag Magnetic Field Strength Tab allows the bidirectional selection of the following Magnetic Field Strength dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Elec/Mag | ||
| Magnetic Field Strength | ||
| oersted | ||
| ampere per meter (A/m) |
Magnetic Flux Tab
The second Minor Tab under the Elec/Mag Major Tab is the Magnetic Flux Tab (see Figure 3.6-2). This example shows the conversion of maxwell to nanoweber. In this example, the amplitude of maxwell is set equal to one (1.0). The conversion equation is shown in Example 3.6-2.
maxwell (Mx) (=1.0) to nanoweber (nWb) Example 3.6-2:
nWb | = | maxwell * Wb/Mx * nWb/Wb |
= | maxwell * 10-8 * 109 | |
= | maxwell * 10 | |
= | 1.0E+1 nWb |
Where: nWb | = | the number of nanoweber calculated |
Mx | = | the starting number of maxwell (1.0) |
Wb/Mx | = | the conversion factor from maxwell to weber (10-8) |
nWb/Wb | = | the conversion factor from weber to nanoweber (109) |
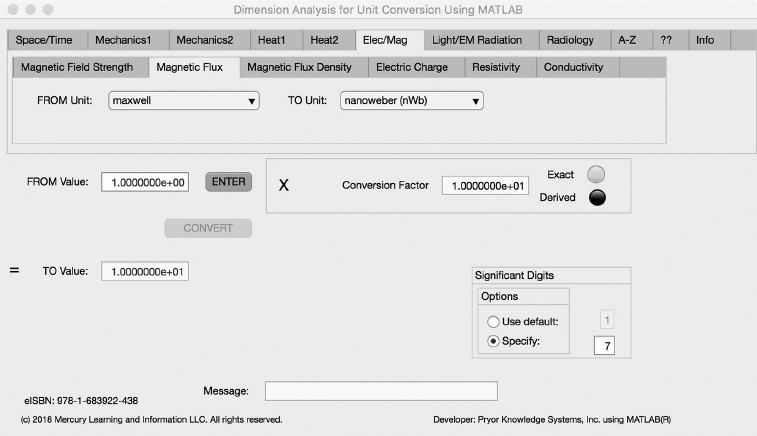
FIGURE 3.6-2 Unit Converter Using MATLAB App - Elec/Mag Magnetic Flux Tab.
And:
The resulting solution is:
nWb = 1.0 * 10 = 10 nanoweber | (3.6-2) |
The Elec/Mag Magnetic Flux Tab allows the bidirectional selection of the following magnetic flux dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Elec/Mag | ||
| Magnetic Flux | ||
| maxwell (Mx) | ||
| nanoweber (nWb) |
Magnetic Flux Density Tab
The third Minor Tab under the Elec/Mag Major Tab is the Magnetic Flux Density Tab (see Figure 3.6-3). This example shows the conversion of gauss to millitesla. In this example, the amplitude of gauss is set equal to one (1.0). The conversion equation is shown in Example 3.6-3.
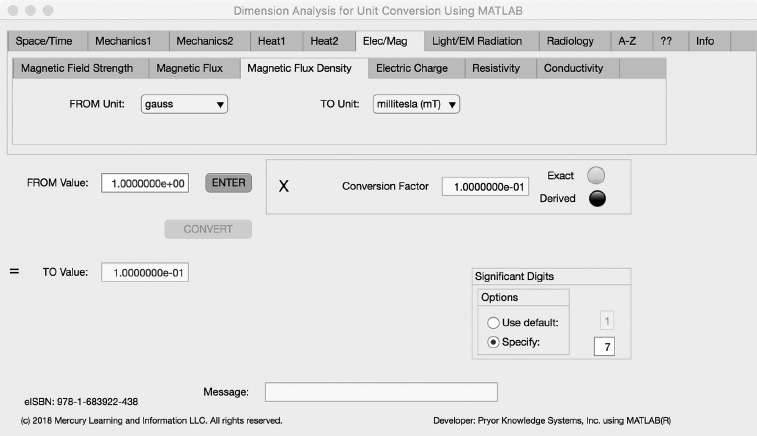
FIGURE 3.6-3 Unit Converter Using MATLAB App - Elec/Mag Magnetic Flux Density Tab.
gauss (G) to millitesla (mT) Example 3.6-3:
mT = G * T/ G * mT/T = G * 10-4 * 103 = gauss * 1.0E-1
Where: mT | = | the number of millitesla calculated |
G | = | the number of gauss to be converted (1.0) |
T/G | = | the conversion factor from gauss to tesla (10-4) |
mT/T | = | the conversion factor from tesla to millitesla (103) |
And:
The resulting solution is:
mT = 1.0 * 1.0E-1 = 1.0E-1 millitesla | (3.6-3) |
The Elec/Mag Magnetic Flux Density Tab allows the bidirectional selection of the following Magnetic Flux Density dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Elec/Mag | ||
| Magnetic Flux Density | ||
| gauss (G) | ||
| millitesla (mT) |
Electric Charge Tab
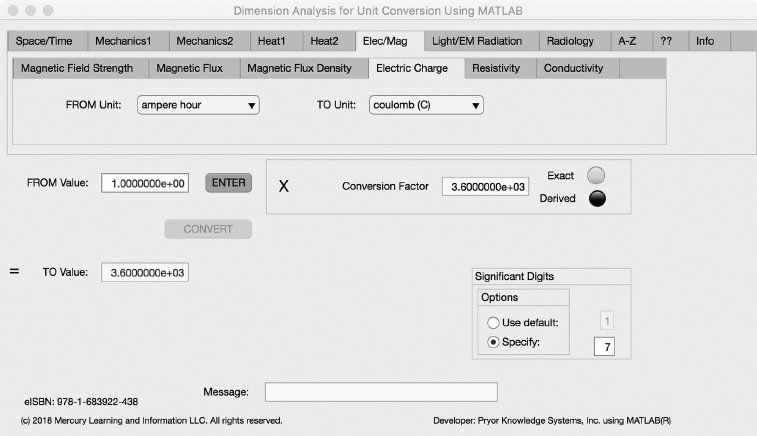
FIGURE 3.6-4 Unit Converter Using MATLAB App - Elec/Mag Electric Charge Tab.
The fourth Minor Tab under the Elec/Mag Major Tab is the Electric Charge Tab (see Figure 3.6-4). This example shows the conversion of ampere hour to coulomb. In this example, the amplitude of ampere hour is set equal to one (1.0). The conversion equation is shown in Example 3.6-4.
ampere hour (A*h) (=1.0) to coulomb (C) Example 3.6-4:
C | = | A*h * (C/s)(1/A) * min/h * s/min |
= | A*h * 1 * 60 * 60 | |
= | A*h * 3600 = A*h * 3.6E+3 |
Where: C | = | the number of coulomb calculated |
A*h | = | the number of ampere hour to be converted (1.0) |
(C/s)(1/A) | = | the conversion factor from ampere to coulomb per second (1) |
min/h | = | the conversion factor from hours to minutes (60) |
s/min | = | the conversion factor from minutes to seconds (60) |
And:
The resulting solution is:
C = 1.0 * 3.6E+3 = 3.6E+3 coulomb | (3.6-4) |
The Elec/Mag Electric Charge Tab allows the bidirectional selection of the following Electric Charge dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Elec/Mag | ||
| Electric Charge | ||
| ampere hour (A*h) | ||
| coulomb (C) |
Resistivity Tab
The fifth Minor Tab under the Elec/Mag Major Tab is the Resistivity Tab (see Figure 3.6-5). This example shows the conversion of ohm circular mil per foot to Nanoohm meter (nOhm * m). In this example, the amplitude of ohm circular mil per foot is set equal to one (1.0). The conversion equation is shown in Example 3.6-5.
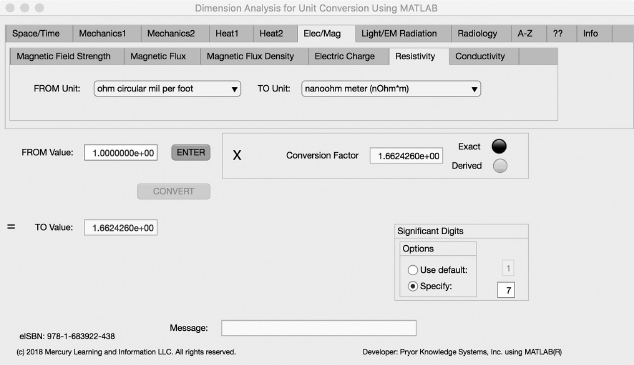
FIGURE 3.6-5 Unit Converter Using MATLAB App - Elec/Mag Resistivity Tab.
ohm circular mil per foot (Ω*cmil/ft) (=1.0) to nanoohm meter (nΩ * m) Example 3.6-5:
nΩ* m | = | Ω*cmil/ft * nΩ/Ω * m2/cmil * ft/m |
= | Ω*cmil/ft * 1.0E+9 * 5.067075E-10 * 1/0.3048 | |
= | Ω*cmil/ft * 1.662426E+0 |
Where: nΩ * m | = | the number of nanoohm meter calculated |
Ω*cmil/ft | = | the number of ohm circular mil per foot to be converted (1.0) |
nΩ/Ω | = | the conversion factor from ohm to nanoohm (1.0E+9) |
m2/cmil | = | the conversion factor from circular mil to meter squared (5.067075E-10) |
ft/m | = | the conversion factor from meter to foot (1/0.3048) |
And:
The resulting solution is:
nΩ * m = 1.0 * 1.662426E+0 = 1.662426E+0 nanoohm meter | (3.6-5) |
The Elec/Mag Resistivity Tab allows the bidirectional selection of the following Resistivity dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Elec/Mag | ||
| Resistivity | ||
| ohm circular mil per foot | ||
| nanoohm meter (nΩ * m) |
Conductivity Tab
The sixth Minor Tab under the Elec/Mag Major Tab is the Conductivity Tab (see Figure 3.6-6). This example shows the conversion of mho per centimeter (mho/cm) to siemens/meter (S/m). In this example, the amplitude of mho per centimeter (mho/cm) is set equal to one (1.0). The conversion equation is shown in Example 3.6-6.

FIGURE 3.6-6 Unit Converter Using MATLAB App - Elec/Mag Conductivity Tab.
mho per centimeter (mho/cm) (=1.0) to siemens per meter (S/m) Example 3.6-6:
S/m | = | mho/cm * cm/m * S/mho |
= | mho/cm * 100 * 1.0 | |
= | mho/cm * 100 = mho/cm * 1.0E+2 |
Where: S/m | = | the number of siemens per meter calculated |
mho/cm | = | the number of mho per centimeter to be converted (1.0) |
cm/m | = | the conversion factor from meter to centimeter = 100 |
S/mho | = | the conversion factor from mho to siemens (1.0) |
And:
The resulting solution is:
S/m = 1.0 * 100 = 100 siemens per meter | (3.6-6) |
The Elec/Mag Conductivity Tab allows the bidirectional selection of the following conductivity dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Elec/Mag | ||
| Conductivity | ||
| mho per centimeter (mho/cm) | ||
| siemens per meter (S/m) |
3.7 QUANTITIES OF LIGHT AND RELATED ELECTROMAGNETIC RADIATION (LIGHT/EM RADIATION)
Figure 3.7-0 shows the Unit Converter MATLAB App Front Panel with the Light and Related Electromagnetic Radiation (Light/EM Radiation) Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Tabs available in the App is explored herein.
FIGURE 3.7-0 Unit Converter Using MATLAB App - Front Panel Light/EM Radiation Tab.
Wavelength Tab
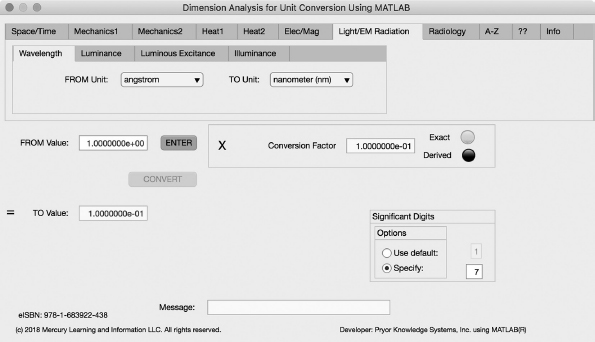
FIGURE 3.7-1 Unit Converter Using MATLAB App - Light/EM Radiation Wavelength Tab.
The first Minor Tab under the Light/EM Radiation Major Tab is the Wavelength Tab (see Figure 3.7-1). This example shows the conversion of angstrom (Å) to nanometer (nm). In this example, the amplitude of angstrom (Å) is set equal to one (1.0). The conversion equation is shown in Example 3.7-1.
angstrom (Å) (=1.0) to nanometer (nm) Example 3.7-1:
nm = Å * m/Å * nm/m = Å * 1.0E-10 * 1.0E9 = Å * 1.0E-1
Where: nm | = | the number of nanometer calculated |
Å | = | the number of angstrom to be converted (1.0) |
m/Å | = | the conversion factor from angstrom to meter (1.0e-10) |
nm/m | = | the conversion factor from meter to nanometer (1.0E9) |
And:
The resulting solution is:
nm = 1.0 * 1.0E-1 = 1.0E-1 nanometer | (3.7-1) |
The Light/EM Radiation Wavelength Tab allows the bidirectional selection of the following wavelength dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Light/EM Radiation | ||
| Wavelength | ||
| angstrom (Å) | ||
| nanometer (nm) |
Luminance Tab
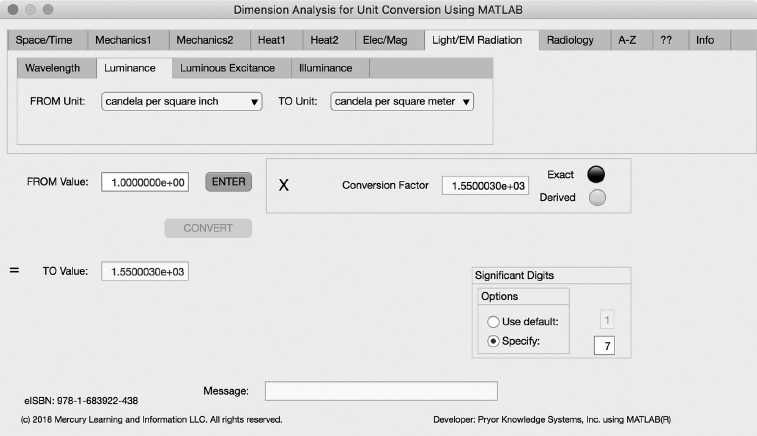
FIGURE 3.7-2 Unit Converter Using MATLAB App - Light/EM Radiation Luminance Tab.
The second Minor Tab under the Light/EM Radiation Major Tab is the Luminance Tab (see Figure 3.7-2). This example shows the conversion of candela per square inch (cd/in2) to candela per square meter (cd/m2). In this example, the amplitude of candela per square inch (cd/in2) is set equal to one (1.0). The conversion equation is shown in Example 3.7-2.
candela per square inch (cd/in2) (-1.0) to candela per square meter (cd/m2) Example 3.7-2:
cd/m2 | = | cd/in2 * in2/ m2 |
= | cd/in2 * 1/6.4516E-4 | |
= | cd/in2 * 1.550003E+3 |
Where: cd/m2 | = | the number of candela per square meter calculated |
cd/in2 | = | the number of candela per square inch to be converted (1.0) |
in2/ m2 | = | the conversion factor from square meter to square inch (1.550003E+3) |
And:
The resulting solution is:
cd/m2 = 1.0 * 1.550003E+3 = 1.550003E+3 candela per square meter | (3.7-2) |
The Light/EM Radiation Luminance Tab allows the bidirectional selection of the following luminance dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Light/EM Radiation | ||
| Luminance | ||
| lambert (L) | ||
| candela per square inch (cd/in2) | ||
| footlambert | ||
| candela per square meter (cd/m2) |
Luminous Excitance Tab
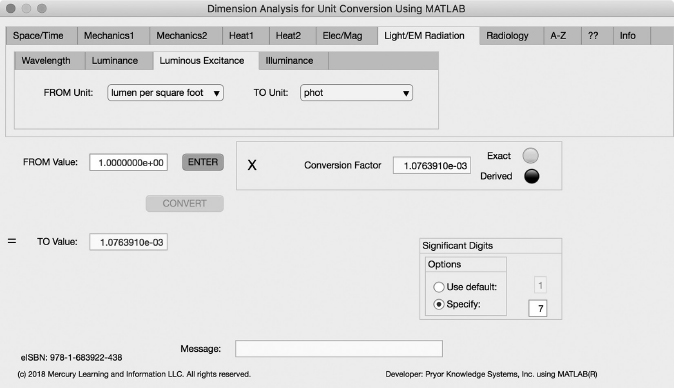
FIGURE 3.7-3 Unit Converter Using MATLAB App - Light/EM Radiation Luminous Excitance Tab.
The third Minor Tab under the Light/EM Radiation Major Tab is the Luminous Excitance Tab (see Figure 3.7-3). This example shows the conversion of lumen per square foot (lm/ft2) to phot (ph = lumen per square centimeter). In this example, the amplitude of lumen per square foot (lm/ft2) is set equal to one (1.0). The conversion equation is shown in Example 3.7-3.
lumen per square foot (lm/ft2) to phot (ph) Example 3.7-3:
ph | = | lm/ft2 * ft2/m2 * m2/cm2 |
= | lm/ft2 * 1/0.09290304 * 1/104 | |
= | lm/ft2 * 0.00107639 = lm/ft2 * 1.07639E-3 |
Where: ph | = | the number of phot calculated |
lm/ft2 | = | the number of lumen per square foot to be converted (1.0) |
in2/m2 | = | the conversion factor from square meter to square foot (1/0.09290304) |
m2/cm2 | = | the conversion factor from square centimeter to square meter (1/104) |
And:
The resulting solution is:
ph = 1.0 * 1.07639E-3 = 1.07639E-3 phot | (3.7-3) |
The Light/EM Radiation Luminous Excitance Tab allows the bidirectional selection of the following Luminous Excitance dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Light/EM Radiation | ||
| Luminous Excitance | ||
| lumen per square foot (lm/ft2) | ||
| phot (ph) | ||
| lux (lx) |
Illuminance Tab
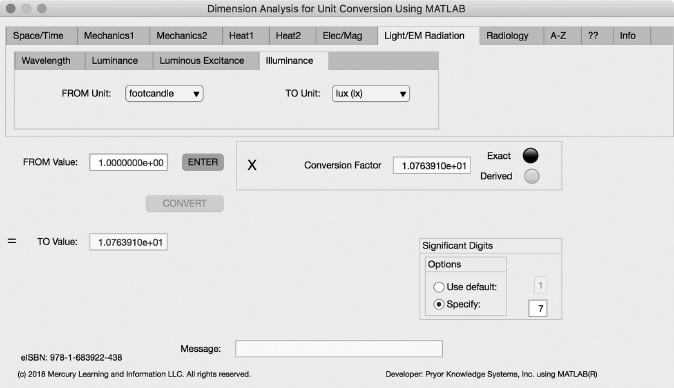
FIGURE 3.7-4 Unit Converter Using MATLAB App - Light/EM Radiation Illuminance Tab.
The fourth Minor Tab under the Light/EM Radiation Major Tab is the Illuminance Tab (see Figure 3.7-4). This example shows the conversion of footcandle (fc = lumen per square foot) to lux (lx = lumen per square meter). In this example, the amplitude of footcandle (fc) is set equal to one (1.0). The conversion equation is shown in Example 3.7-4.
footcandle (fc) to lux (lx) Example 3.7-4:
lx | = | fc * ft2/m2 |
= | fc * 1/0.09290304 | |
= | fc * 10.76391 | |
= | fc * 1.076391E+1 |
Where: lx | = | the number of lux calculated |
fc | = | the number of footcandle to be converted (1.0) |
ft2/m2 | = | the conversion factor from square meter to square foot (1.07639E+1) |
And:
The resulting solution is:
lx = 1.0 * 1.07639E+1 = 1.07639E+1 lux | (3.7-4) |
The Light/EM Radiation Illuminance Tab allows the bidirectional selection of the following illuminance dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Light/EM Radiation | ||
| Illuminance | ||
| footcandle | ||
| lux (lx) |
3.8 QUANTITIES OF RADIOLOGY
FIGURE 3.8-0 Unit Converter Using MATLAB App - Front Panel Radiology Tab.
Figure 3.8-0 shows the Unit Converter MATLAB App Front Panel with the Radiology Tab selected. Bidirectional matrices were created and installed within this app to allow the user the ability to easily select via pull-down menus all of the desired conversion pairs required. Each of the Tabs available in the App is explored herein.
Activity (of a radionuclide) Tab
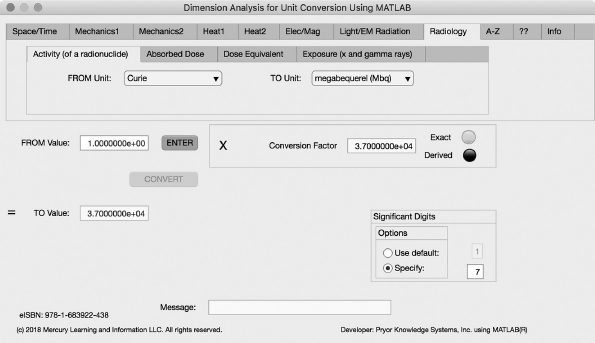
FIGURE 3.8-1 Unit Converter Using MATLAB App - Radiology Activity (of a radionuclide) Tab.
The first Minor Tab under the Radiology Major Tab is the Activity (of a radionuclide) Tab (see Figure 3.8-1). This example shows the conversion of Curie (ci) = 3.7×1010 decays per second) to megabequerel (MBq; 1 Bq = 1 decay per second). In this example, the amplitude of Curie (ci) is set equal to one (1.0). The conversion equation is shown in Example 3.8-1.
Curie (ci) to megabequerel (MBq) Example 3.8-1:
MBq | = | ci * Bq/ci * MBq/Bq |
= | ci * = ci * 3.7E+10 * 1.0E-6 | |
= | ci * 3.7E+4 |
Where: MBq | = | the number of megabequerel calculated |
ci | = | the number of Curie to be converted (1.0) |
Bq/ci | = | the conversion factor from Curie to bequerel (3.7E+10) |
MBq/Bq | = | the conversion factor from bequerel to megabequerel (1.0E-6) |
And:
The resulting solution is:
MBq = 1.0 * 3.7E+4 = 3.7E+4 megabequerel | (3.8-1) |
The Radiology Activity (of a radionuclide) Tab allows the bidirectional selection of the following Activity (of a radionuclide) dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Radiology | ||
| Activity (of a radionuclide) | ||
| Curie | ||
| megabequerel (MBq) |
Absorbed Dose Tab
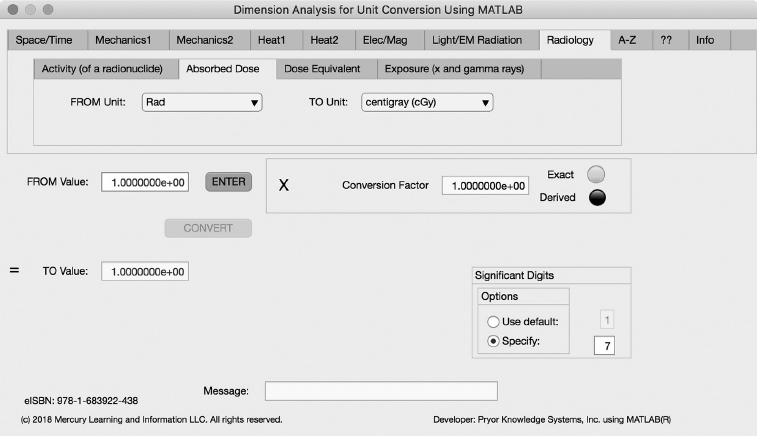
FIGURE 3.8-2 Unit Converter Using MATLAB App - Radiology Absorbed Dose Tab.
The second Minor Tab under the Radiology Major Tab is the Absorbed Dose Tab (see Figure 3.8-2). This example shows the conversion of Rad to centigray (cGy). In this example, the amplitude of Rad is set equal to one (1.0). The conversion equation is shown in Example 3.8-2.
Rad to centigray (cGy) Example 3.8-2:
cGy | = | rad * Gy/rad * cGy/Gy |
= | rad * 0.01 * 1.0E+2 | |
= | rad * 1.0E0 |
Where: cGy | = | the number of centigray calculated |
Rad | = | the number of Rad to be converted (1.0) |
Gy/Rad | = | the conversion factor from Rad to gray (0.01) |
cGy/Gy | = | the conversion factor from gray to centigray (1.0E+2) |
And:
The resulting solution is:
cGy = 1.0 * 1.0E+0 = 1.0E0 centigray | (3.8-2) |
The Radiology Absorbed Dose Tab allows the bidirectional selection of the following absorbed dose dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Radiology | ||
| Absorbed Dose | ||
| Rad (rad) | ||
| gray (Gy) | ||
| centigray (cGy) |
Dose Equivalent
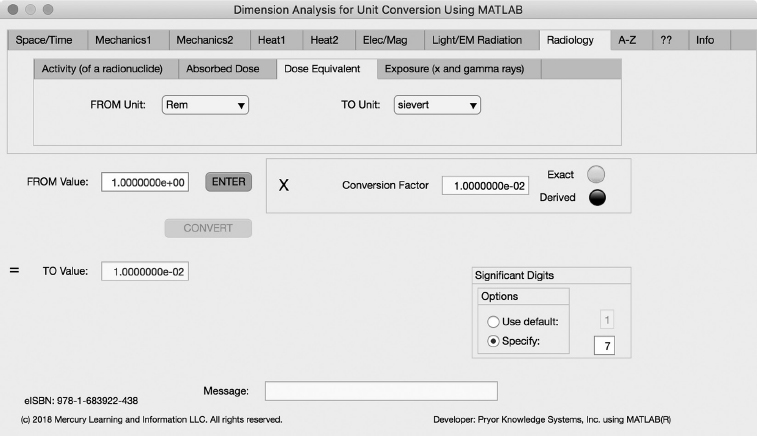
FIGURE 3.8-3 Unit Converter Using MATLAB App - Radiology Dose Equivalent Tab.
The third Minor Tab under the Radiology Major Tab is the Dose Equivalent Tab (see Figure 3.8-3). This example shows the conversion of Rem (rem) to sievert (Sv). In this example, the amplitude of Rem (rem) is set equal to one (1.0). The conversion equation is shown in Example 3.8-3.
Rem (rem) to sievert (Sv) Example 3.8-3:
Sv = rem * Sv/rem = rem* 0.01 = rem * 1.0E-2
Where: Sv | = | the number of sievert calculated |
rem | = | the number of Rem to be converted (1.0) |
Sv/rem | = | the conversion factor from Rem to sievert (0.01) |
And:
The resulting solution is:
S = 1.0 * 1.0E-2 = 1.0E-2 sievert | (3.8-3) |
The Radiology Dose Equivalent Tab allows the bidirectional selection of the following dose equivalent dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Radiology | ||
| Dose Equivalent | ||
| Rem (rem) | ||
| sievert (Sv) |
Exposure (x and gamma rays) Tab
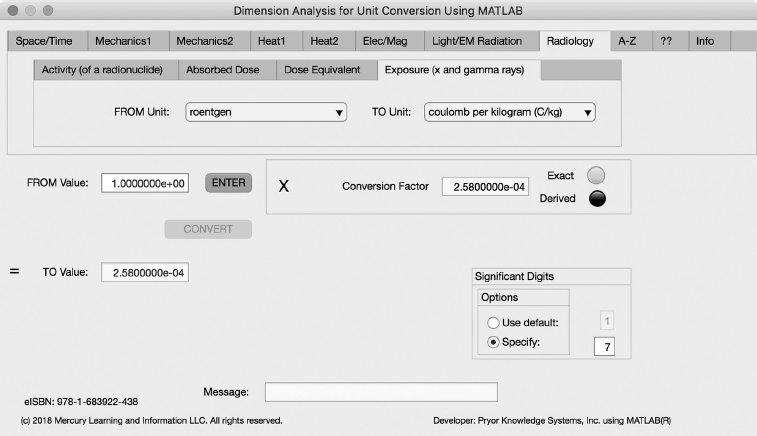
FIGURE 3.8-4 Unit Converter Using MATLAB App - Radiology Exposure (x and gamma rays) Tab.
The fourth Minor Tab under the Radiology Major Tab is the Exposure (x and gamma rays) Tab (see Figure 3.8-4). This example shows the conversion of roentgen (R = lumen per square foot) to coulomb per kilogram (C/kg = lumen per square meter). In this example, the amplitude of roentgen (R) is set equal to one (1.0). The conversion equation is shown in Example 3.8-4.
roentgen (R) to coulomb per kilogram (C/kg) Example 3.8-4:
C/kg = R * (C/kg)/R = R * 0.000258 = R * 2.58E-4
Where: C/kg | = | the number of coulomb per kilogram calculated |
R | = | the number of roentgen to be converted (1.0) |
(C/kg)/R | = | the conversion factor from roentgen to coulomb per kilogram (0.000258) |
And:
The resulting solution is:
C/kg = 1.0 * 2.58E-4 = 2.58E-4 coulomb per kilogram | (3.8-4) |
The Radiology Exposure (x and gamma rays) Tab allows the bidirectional selection of the following exposure (x and gamma rays) dimensions:
| Major-Tab | Minor-Tab | Units on Pull-Down |
| Radiology | ||
| Exposure (x and gamma rays) | ||
| roentgen (R) | ||
| coulomb per kilogram (C/kg) |