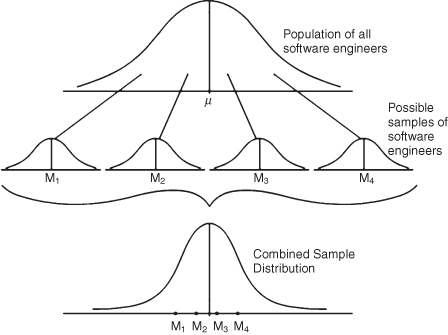
Figure SPUB.1. Creating a sampling distribution.
STATISTICAL PROCEDURES UNIT B: THE NATURE OF INFERENTIAL STATISTICS1
Descriptive statistics examine the ways a set of scores or observations can be characterized. Is the set of scores normally distributed? What is the most characteristic indicator of central tendency? Are there extreme scores? What information about the nature of the scores can be obtained from examining histograms and other graphs?
Thus far, we have examined raw score distributions made up of individual raw score values. For example, a set of 40 schools each had percentages of students qualified for FR, or percentages of students passing math and reading achievement scores. We tried to understand the nature of these variables; whether they were normally distributed and how the percentages were distributed compared to the standard normal distribution.
In the real world of research and statistics, practitioners almost always deal with sample values, since they very rarely have access to population information. Thus, for example, we might want to understand whether the job satisfaction ratings of a sample of 100 software engineers is characteristic of all software engineers, not just our 100. Since it is practically impossible to get job satisfaction ratings for all software engineers, we must measure the extent to which sample values approximate or estimate the overall population values. We are using the picture at hand (of our sample group) to get a better picture of the overall (population) group that we have no way of picturing.
Inferential statistics are methods to help us make decisions about how real-world data indicate whether dynamics at the sample level are likely to be related to dynamics at the population level. That is to say, we need to start thinking about our sample distribution of software engineers as being one possible sample group of 100 taken from the overall population compared to a number of other such samples (of 100) that could be taken. We can then study our sample and see how the statistical information might compare to the average set of information derived from all the other possible sample groups. Is our sample mean, for example, likely to be close to the average mean of all the other sample groups?
Take a look at Figure SPUB.1. This figure shows that if you were to take repeated samples from the population of software engineers (we have only shown four samples, but in theory, you would take many samples), you could take just the mean values from each of the samples and make up a separate “combined” distribution of samples. If we were to then take our study sample of 100 software engineers, we could see how our study mean value compares to all the other sample means. If the study mean was close to the mean of the set of sample means, we could say that our sample mean is representative of the population mean (Figure SPUB.1).
Figure SPUB.1. Creating a sampling distribution.

What we just described is actually a basic principle of inferential statistics known as the central limit theorem. Statisticians who have gone before us discovered several things about taking repeated samples from distributions. In the central limit theorem, they found that means of repeated samples taken from a population will form a standard normal distribution (assuming a large sample size) even if the population was not normally distributed. The combined sampling distribution that results will have important properties to researchers conducting inferential studies.
The combined sampling distribution would have the following properties:
As you can see in Figure SPUB.1, the four hypothetical samples are taken from the population, and their individual means make up a separate distribution (the combined sampling distribution). You can see that the individual means, which represent their sample distributions (M1, M2, M3, M4), lay close to the population mean in the new distribution. Figure SPUB.1 shows this process using only four samples for illustration. In real-life studies, the researcher does not have to take repeated samples from the population. Because of the long history we have of statistical measurement, we can accept the fact that the theorem is valid and we can use it in our study.
Here is how we could use the central limit theorem in an actual study.
Here are some possible results:
If you have taken a class in statistics, you will recognize the previous example as a (single sample) t test. In terms of our possible outcomes, The first outcome would indicate that a job satisfaction contentment training program was not effective. It was therefore not judged to be statistically significant. In this case, that means the sample mean was not far enough away from the population mean to conclude they were likely not the same sorts of software engineers.
The second outcome (for either reason) would indicate a statistically significant difference between the sample mean and the population mean if the sample mean value was far enough away from the population mean. In this case, the sample mean would be considered an unlikely value to have just happened by chance (statisticians usually consider values beyond the middle 95 percent of the standard normal curve to be significant, thus making a conclusion like “significant beyond the 0.05 level”).
If we concluded that the sample was significantly different from the population mean because it reflected some policy or training that we did, we would have confidence in the power of our training. If we concluded that the sample was different because it was a weird sample, then we might say that this finding was really in error (statisticians would call this an alpha error or assuming a finding was significant when it really shouldn’t have been).
In summary, inferential statistics is a process of comparing a sample value (or set of sample values) to an unknown population value (or values) based on time-tested statistical principles. We have therefore seen that a researcher’s sample values can be used to make statistical decisions (i.e., statistically significant) or conclusions about the likelihood of differences being the result of some action on the part of the researcher (policy or training) or on the basis of error.
We just used the example of a single sample t test. Since more complex research designs use more than one sample group (i.e., experimental group versus control group in an experiment), there are other statistical tests that use different formulas to make the same kinds of conclusions. Each statistical test (if they are parametric) compares a sample value or values to population values using a sampling distribution.
For example, if we used two sample groups of software engineers (giving one the training and the other not), we could see if the difference between our sample groups was similar to the difference between all possible sets of sample group differences). This would be an independent samples t test. If we had used three such samples (giving one group no training, one group slight training, and one group intensive training), we would use an ANOVA (analysis of variance) to decide whether there we significant differences between the sample group means (relative to the sampling distribution of variances).
In all these cases, we are comparing sample values to population values, not examining individual scores within a sample. We no longer think of our sample values individually, but as one set that could be derived from a population along with many more such sets; our sample set of values are now seen as simply one possible set of values alongside many other possible sample sets. That is the difference between inferential and descriptive statistics. We therefore change the nature of our research question:
Human actions are rarely, if ever, determined, but they are fairly predictable. One has only to consider the many ways in which the things we (think) we choose to do are really those things that are expected. Marketing specialists have made billions of dollars on this principle by targeting baby boomers. Sociologically, when people repeat actions in society, they create patterns (or ruts) that persist. Think of the many ritualized behaviors you enact every day. (For example, one of us has a very rigid schedule in the morning that starts with making coffee; changing this would be catastrophic!) The result is that human behavior can be characterized by predictability.
When we speak of predictable actions, we note that when actions are repeated, they form “ruts” which come to typify behavior. Thus, presented with a similar situation, the individual most likely follows the behavior that creates the rut. For example, when someone arises in the morning, they may typically make coffee and read the newspaper. They are equally free to do other behaviors (weed the garden, drive their car onto a lawn, etc.), but they will most likely make coffee. Over time, they have repeated this behavior, and it becomes almost second nature. Strictly speaking, Probability is the field of mathematics that studies the likelihood of certain events happening out of the total number of possible events. Thus, what are the chances that a poker player will draw a five of hearts if they need it to complete their straight flush? All the available cards have an equal chance of being chosen (unless the dealer is a crook), so how likely is the player to get their card? Stated in formula language, empirical probability is simply the number of occurrences of a specific event divided by the total number of possible occurrences. So, whether a player gets the five of hearts presents a probability of one card divided by the remaining cards in the deck of cards. This is different from the “predictable” language of probability we noted earlier. Formally, probability deals with independent possibilities (the likelihood of a five of hearts out of the remaining cards), whereas using predictable choices represents dependent possibilities since each action has been affected by previous actions.
We have already seen that behaviors, attitudes, and beliefs have a great deal of variability. Why is there such variability? Why do people not always believe the same thing and act the same way? In descriptive statistics, we learn the ways to understand the extent of the variability and whether the resultant distribution of behaviors and beliefs conforms to a normal distribution. But that does not explain the why.
Human actions and beliefs have many causes. We cannot understand all of them. The fact that variance exists may be due to our inability to understand the full range of forces acting on the individual at any particular moment. But it may also exist because we cannot fully explicate individual choice or action.
Probability involves the realm of expectation. By observing and measuring actions and behaviors over time, we develop expectations that can help us better predict outcomes. If we observe that a group of workers produce a certain sick time ratio (for example 15 percent of total days worked), we might predict the same outcome on future occasions if there are no changes in working conditions or company policy. Our expectation, being based in observation, will help us predict more accurately. This still does not explain why the workers take the same amount of sick time, but it does point out an area for investigation. We may never discover all the reasons for sick time rates, but the study of probability gets us closer to a more comprehensive understanding.
If you think about the normal curve, you will realize that human actions can take a number of different courses. Most responses tend to be clustered together, but there will be some responses that fall in different directions away from the main cluster. Therefore, we can think of the normal curve as a visual representation of the fact that we do not have certainty, but probability in matters of such things as attitudes and buying behavior, test scores, and aptitudes.
In inferential statistics, statisticians think of the normal curve in terms of probability. Since approximately 68 percent of the area (or a proportion of 0.68) of the normal curve lies between one standard deviation, positive or negative, for example, we can think of any given case having a 0.68 probability of falling between one standard deviation (SD) on either side of the mean.
Knowing what we do of the distribution of area in the standard normal curve, we can observe that possible scores beyond 2 SDs (in either a positive or negative direction) are in areas of the distribution where there are very few cases. Thus randomly selecting a score from a distribution in these small areas would have a much smaller probability than randomly selecting a score nearer the mean of the distribution. In a normally distributed variable, only 5 percent of cases or so will fall outside the ± 2 SD area. Therefore, with 100 cases, selecting a case randomly from this area would represent a probability of 0.05 (since 5/100 = 0.05).
Returning to our example from the earlier section, we can see how the job satisfaction of our software engineer sample might be considered either likely or not likely depending on how the sample value compared to the sampling distribution mean. Consider Figure SPUB.2 that shows one possibility (the significantly different possibility).
Figure SPUB.2. The significance of the study group.
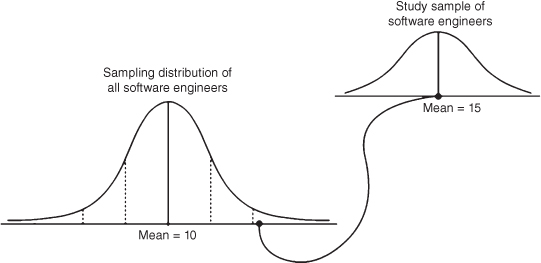
As you can see in the figure, the combined sampling distribution shows a job satisfaction mean of 10 (out of 20 total), and you can see where the SDs fall by the dotted lines. The figure shows a hypothetical result of our study group obtaining a job satisfaction average of 15. When we use the appropriate statistical procedure (t test) to translate the sample mean values into the combined sampling distribution, we see that it falls beyond the cutoff for +2 SDs.
If this was an actual finding, we would conclude that the job satisfaction level of the sample was statistically significantly higher than the population, since the study sample mean fell that far above the population mean. Since 2 SDs (technically ± 1.96 SDs) on a standard normal comparison curve excludes about 5 percent of the area of the curve (and therefore results in a probability of happening by chance of less than 5 percent), the researcher would call this statistically significant. This 5 percent exclusion area is typically the standard by which statistical findings are considered significant. The researcher might therefore conclude that the significant finding had a probability level less than 5 percent, or p < 0.05.
The p values that are reported in statistical studies therefore correspond to the probability of obtaining a given finding by chance. Each statistical procedure has nuances for how this is expressed, but essentially it is shorthand for how statisticians decide whether or not a given finding is excessive, relative to the sampling distribution information.
Parameters refer to measures of entire populations and population distributions. This is distinguished from statistics, which refer to measures of sample data taken from populations. We need to distinguish these measures, since inferential statistics is quite specific about the measures available for analysis. As you progress in using research designs and appropriate statistical applications, you will find that statisticians and researchers distinguish population values from sample values in their symbols; population parameters are typically represented by Greek symbols.
Hypotheses tests are the formal logical processes established to make a scientific decision. The decisions that result from a hypothesis test are typically couched in terms of the probability levels of the outcome and the extent to which you can say whether or not a finding is statistically significant. Ultimately, the process is used to support or refute a hypothesis so that a researcher can make a statistical decision about a specific research problem and possibly inform a theory.
There is a generally agreed upon set of steps that form the general procedure for a hypothesis test (with some variations for each statistical procedure). Here are the steps with our (contrived) results applied so you can see how it works:
In probability terms, any finding of p < 0.05 is considered statistically significant. Researchers and statisticians have a specific definition for statistical significance: it refers to the likelihood that a finding we observe in a sample is too far away from the population parameter (in this case the population mean) by chance alone to belong to the same population.
Recall our discussion of effect size in former sections. Researchers and statisticians have relied extensively on statistical significance in the past to help make statistical decisions. You can see how this language (i.e., using p values) permeates much of the research literature; it is even widespread among practitioners and those not familiar with statistical procedures.
The emphasis in statistics and research now is on practical significance, or effect size, which refers to the impact of a finding, regardless of its statistical p value. The two issues are related to be sure. However, effect size addresses the issue of the extent to which a difference or treatment in a test of difference results in extreme test values. That is, how much impact does a research variable have to achieve in order to result in a change in a sample value?
Consider our hypothetical finding. We might reject the null hypothesis and conclude a statistically significant result. But this finding only has to do with the probability of whether the finding is a chance finding. The effect size consideration is a completely different issue. It does not concern itself with probability, but rather how far away from the population mean has our sample mean ended up from the population mean? In practical terms, this would be like saying, “The p values are fine, but I am astounded to find out that my software engineers are 40 percent more satisfied [or whatever, I just made up the number] than the typical software engineer. My training program must really be working well (or something else I do not see might be causing the job satisfaction to be higher).”
Note
1 Parts of this section are adapted from M. L. Abbott, Understanding Educational Statistics Using Microsoft Excel® and SPSS® (Wiley, 2011), by permission of the publisher.