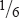
Peirce wrote this undated letter in the second half of August 1910. It is most likely a response to a letter Carus had sent him in which he practically threatened Peirce that he would publish the Illustrations whether Peirce sent him corrections or not. The letter is preceded by an aborted July 19, 1910 draft in which Peirce aimed to explain the corrections he deemed “indispensable in the reprint of my Popular Science Monthly papers” (RL 77:208–18). In that letter, Peirce, having tried hard to rewrite the first two Illustrations articles in the previous year, agreed to republish the Illustrations in its original form, prefaced by a note explaining a major error that needed to be corrected. Peirce wrote this letter such that it could act as the printer’s copy for that preface, writing “only on one side of the paper, so that, if I would suddenly die in one of the fits to which I am almost daily subject, what I write could be set up and printed.” Both in the July draft and in the letter printed below, Peirce took the main error of the Illustrations to lie in its nominalism, even though in his own estimation he had already moved away from that at the time. As he explains in the draft:
The greatest and most decisive of all questions of metaphysics, is, according to the way of thinking which has gradually ripened in me since 1873 (which is the date of my formulating the opinion expressed in the two articles that are the two parts of that Essay on Pragmatistic Clearness),1 is the question whether generals are real; which question I would like to phrase as Whether anything Indeterminate is Real (since we define an Individual, meaning what is the contrary of a General, or that which is omni modo determinatum),2 and which question I would supplement by asking Whether anything Indefinite is Real.
Unfortunately, the July draft breaks off before the nominalism-realism discussion really gets underway. In the August letter, reprinted below, Peirce reiterates the plan of publishing the Illustrations virtually unaltered and adding a preface “in which I state in general terms how what I then say ought to be altered.” This time, however, the letter does not contain the preface, even if in draft form, but is much more preliminary, nor is it limited to the main error of the series, its nominalism, as it also addresses issues with the later articles, especially his account of the doctrine of chances, distinguishing probability from both plausibility and likelihood. In addition Peirce is suggesting adding a discussion of the existential graphs, an idea that is very skeptically received by Open Court.
Paul Carus received the letter on August 29, 1910 and immediately forwarded it to Francis C. Russell whom he charged with readying the Illustrations for publication. Russell had three copies made at the Open Court office in Chicago: one for himself, one for Carus, and one for Peirce. The last was sent to Peirce on September 17, 1910 together with the original holograph letter. The holograph letter is preserved in Peirce’s papers at Harvard’s Houghton Library (RL 77: 220–41), with the exception of the first sheet, which seems to be lost. Of the typescript sent to Peirce, only the first sheet was found (RL 77:242). The remaining two typescripts survive in the Open Court Collection at the Morris Library of Southern Illinois University in Carbondale (Coll. 27, Box 91), one containing corrections made by Russell (comparing the typescript with the original letter), the other containing only a few corrections by Carus. The letter is included in Volume 8 of the Collected Papers (CP 8.214–38), albeit with significant omissions. A more detailed discussion is found in the introduction.
My Dear Doctor Carus:*
Ever since I was paid that money by you and Mrs. Carus, I have been engaged with all my energy, allowing only for such as I had to expend upon my wife’s health and upon getting this house habitable and in salable condition, in trying to write an article or articles for you upon the second grade of clearness,3 i.e., that which results from analytic definition and upon corrections to the errors and other faults of the articles of mine that appeared in the Popular Science Monthly in 1877 and 18784 to which I should be glad if you would add a reprint of the article of January, 1901 which requires no correction.5
I have written a great deal but am satisfied with but the smaller part of it, and the result is that I worked, until,—what with worries, too,—I was in a state of downright nervous exhaustion from which I have now been for a good number of months recovering, but owing to the decay of my powers and being so sick of writing about the same things, I cannot even write yet but a few equivalents of pages of this letter very slowly and for not over three hours and with many days when I can do nothing. Since I got your letter I have—often trying in vain to accelerate my speed,—the slowness of which is largely due to the labor of writing with the extreme precision required, gradually been forced to the conclusion that since you are very reasonably impatient, my best course is simply to write a preface in which I state in general terms how what I then say ought to be altered, and I will here (if my strength holds out) try to indicate the points I should make.
In regard to the first Essay consisting of the first two articles, the principal positive error is its nominalism, especially as illustrated by what I said about Gray’s stanza, “Full many a gem” etc., pp. 3 to 5 et seq.6 I must show that the will be’s, the actually is’s, and the have beens are not the sum of the reals. They only cover actuality. There are besides would be’s and can be’s that are real. The distinction is that the actual is subject both to the principles of contradiction and of excluded middle; and in one way so are the would be’s and can be’s. In that way a would be is but the negation of a can be and conversely.* But in another way a would-be is not subject to the principle of excluded middle; both would be X and would be not-X may be false. And in this latter way a can be may be defined as that which is not subject to the principle of contradiction. On the contrary, if of anything it is only true that it can be X it can be not-X as well.
It certainly can be proved very clearly that the Universe does contain both would be’s and can be’s.
Then in regard to the second article, I ought to say that my three grades of clearness are not, as I seemed then to think, such that either the first or the second are superseded by the third although we may say that they are acquired,—mostly,—in the order of those numbers. I ought to describe, if only in a paragraph, how to train oneself and one’s children in the first grade of clearness, so that, for example, one will recognize a millimetre length when one meets with it; and so with colors.7 I have done a great deal of work in training myself to this kind of clearness.8 It would if put together amount to two or three years of industry; and I should recommend systematic* exercises of the sort to everybody.9 Useful as that is, however, I don’t hesitate to say that the second grade of clearness is far more important, and all my writings of late years illustrate that.10 Still, I continue to admit that the third grade is the most important of all and a good example of it is Wm. James who is so phenomenally weak in the second grade, yet ever so high above most men in the third. But there is no reason why all three should not be symmetrically developed.
The bulk of these Popular Science articles, after the first two, are occupied with a criticism of the underlying principles of Laplace’s Théorie analytique des probabilités and Mill’s System of Logic,—two writers of a high order which have had and still have a great and deplorable influence.11
Before the third article on Probability I should like to insert a short and easy account of my Existential Graphs; because when that system is well in hand, it becomes so much easier to show great faults of Laplace and Mill; and that shorter account, I could now easily write.12
It would also be well to show how all numbers involve essentially nothing but ideas of succession.13 Then I should like to point out how utterly Laplace fails to define what he means by probabilité, his account of it resting upon what he calls the également possibles, which I maintain has none but the vaguest meaning.14 I ought on my side to define probability. For that purpose, I should have to begin by distinguishing three ways—three quite different directions so to speak, as different as the X, Y, Z of a system of orthogonal coördinates—in which cognitions can fall short of absolute certainty,—or rather of mathematical certainty, which is not absolute, because blunders may have been committed in reaching it.
The names which I would propose for general adoption for the three different kinds of acceptability of propositions are
plausibility
verisimilitude
probability†
The last alone seems to be capable of a certain degree of exactitude of measurement.
By plausibility, I mean the degree to which a theory ought to recommend itself to our belief independently of any kind of evidence other than our instinct urging us to regard it favorably. All the other races of animals certainly have such instincts: why refuse them to mankind? Have not all men some notions of right and wrong as well as purely theoretical instincts? For example, if any man finds that an object of no great size in his chamber behaves in any surprising manner, he wonders what makes it do so; and his instinct suggests that the cause, most plausibly, is also in his chamber or in the neighbourhood.
It is true that the alchemists used to think it might be some configuration of the planets; but in my opinion this was due to a special derangement of natural instinct. Physicists certainly today continue largely to be influenced by such plausibilities in selecting which of several hypotheses they will first put to the test.
By verisimilitude I mean that kind of recommendation of a proposition which consists in evidence which is insufficient because there is not enough of it, but which will amount to proof if that evidence which is not yet examined continues to be of the same complexion as that already examined, or if the evidence not at hand and that never will be complete, should be like that which is at hand. All determinations of probability ultimately rest on such verisimilitudes. I mean that if we throw a die 216* times in order to ascertain whether the probability of its turning up a six at any one throw differs decidedly from 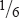
![]() or not, our conclusion is an affair not of probability as Laplace would have it, by assuming that the antecedent probabilities of the different values of the probability are equal, but is a verisimilitude or as we say a “likelihood.” That Laplace is wrong can be demonstrated since his theory leads to contradictory results. But perhaps the easiest way to show it is wrong is to point out that there is no more reason for assuming that all the values of the probability are equally probable than for assuming that all the values of the odds are so; or that all the values of the logarithms of the odds are so, since this is our instinctive way of judging of probabilities, as is shown by our “balancing the probabilities.”
or not, our conclusion is an affair not of probability as Laplace would have it, by assuming that the antecedent probabilities of the different values of the probability are equal, but is a verisimilitude or as we say a “likelihood.” That Laplace is wrong can be demonstrated since his theory leads to contradictory results. But perhaps the easiest way to show it is wrong is to point out that there is no more reason for assuming that all the values of the probability are equally probable than for assuming that all the values of the odds are so; or that all the values of the logarithms of the odds are so, since this is our instinctive way of judging of probabilities, as is shown by our “balancing the probabilities.”
Having thus defined plausibility and verisimilitude, I come to define probability.15 None of the books contain a definition of mathematical probability (which is what I mean by “probability,” however measured) which will hold water. For the sake of simplicity, I will define it in a particular example. If, then, I say that the probability that if a certain die be thrown in the usual way it will turn up a number divisible by 3 (i.e. either 3 or 6) is ⅓, what do I mean? I mean, of course, to state that that die has a certain habit or disposition of behaviour, in its present state of wear. It is a would be and does not consist in actualities or single events in any multitude finite or infinite. Nevertheless a habit does consist in what would happen under certain circumstances if it should remain unchanged throughout an endless series of actual occurrences. I must therefore define that habit of the die in question which we express by saying that there is a probability of ⅓ (or odds of 1 to 2) that if it be thrown it will turn up a number divisible by 3 by saying how it would behave if, while remaining with its shape, etc. just as they are now, it were to be thrown an endless succession of times. Now it is very true that it is quite impossible that it should be thrown an infinite succession of times. But this is no objection to my supposing it, since that impossibility is merely a physical, or, if you please, a metaphysical one, and is not due to any logical impossibility to the occurrence in a finite time of an endless succession of events each occupying a finite time. For when Achilles overtook the tortoise he had to go through such an endless series (endless in the series, but not endless in time) and actually did so; or if he didn’t another did.
Very well, I will further suppose that tallies are kept during the throwings, one tally of the throws turning up 6 or 3, and the other tally of the throws turning up 1, 2, 4, 5; and further I will suppose that after each throw the number that the latter tally has reached shall be divided by the number that the former tally has reached. And I will use the expression that this quotient changes its value at every new throw, instead of saying that a new quotient differs from the last. When the quotient changes from being greater than 2 to being* less than or greater than 2 to being either just 2 or on the opposite side of 2 to what it was before, as for example if it passes from being 21:10 to being 21:11 or from 21:11 to 22:11 or from 25:12 to 25:13, etc., I shall say it touches 2 (meaning strictly that it either comes to 2† or passes across 2). Then after the first throw it will be either 0 or ∞ and there it may remain for any number of throws. But after it has once moved away it never will return to either of these values, but after it has finally recovered from the effects of the first throws it will oscillate in a very irregular way, and soon it will “touch” (or pass over) some other values for the last time although nobody can know that it is to prove to have been for the last time; and then values still nearer to 2 will be touched or traversed for the last time. And in its endless series* there will be no value except only 2 that it would† not touch or traverse for the last time excepting only the value 2. And this “would be” is what constitutes the habit which we state in saying that the odds against its turning up a number divisible by 3 are 2:1, or that the probability of its turning up a 6 or a 3 is ⅓.
Aug 23
I could not write before. Now there are two points to be particularly noticed about the definition of probability. The first is that the probability of an event may be an irrational number. In that case every value of the quotient of one tally divided by the other will get finally left (so that the quotient never again touches or traverses it). Some will be left because they are too small and others because they are too large. But any one you please will get left for one or the other of these two reasons. This must be taken into account in drawing up the definition.
The other point is that our throws and tallies will give the probability in question only on condition that the fact that at certain throws (determined by their ordinal places in the series) had turned up, such and such of them numbers divisible by 3, and the rest of them numbers not of that kind, will make absolutely no difference in the probability that any given throw (determined as above) will turn up a number divisible by three. This statement, of course, refers to what would happen if a series of throws long enough to cover the highest in order of throwing of the determinate throws were to be repeated endlessly.
In short that the numbers turned up are each absolutely independent of what has been or will be turned up on other occasions. This comes to saying that the tallies need not be of consecutive throws but may be every truth or any other endless series so long as whether a given throw be counted on the tally or not is nowise influenced by whether that throw turns up a number divisible by three or another kind of number. The definition must be made explicit upon this point.
[This latter condition will make quite a puzzle for those who deny absolute chance; yet experience proves (far more certainly than it proves determinism), that this condition can be fulfilled in all cases.]16
The definition of probability resulting in this way.
Now from the above definition of probability together with the ordinal definitions of
1. The whole numbers, as expressed in the secundal system in which,

But of course this description is not a definition.
2. Of addition.
3. Of multiplication.
4. Of involution.
5. Of ratio.
6. Of the rational positive values as those which result from putting
N:1 ≡ N
whatever whole cardinal* number (including 0) N may be. And such ratios I call the ratios of the zero grade.
And from running through any complete series of all the ratios† of any given rational‡ grade from any ratio N:1 to N+1:1 inclusive and putting between every successive pair of ratios of grade m, (which two we may denote by p:q and r:s) a new ratio
(p+r):(q+s)
and all the ratios of grade m together with all so inserted constitute the ratios of grade m+1.
And all the ratios of all finite grades are all the positive§ rational values.
7. And if (p:q) [and] (r:s) are two ratios** of the same†† grade, whether successive or not, then if they have different values and p:q is less than r:s then p:q < (p+r):(q+s) < r:s.* But if 
![]() then
then 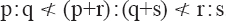
![]() .† And all ratios of real grades‡ are real values and two real values only differ by what other real values one higher (or lower) than which the other is not. From these definitions I will deduce every valid rule of the doctrine of chances.
.† And all ratios of real grades‡ are real values and two real values only differ by what other real values one higher (or lower) than which the other is not. From these definitions I will deduce every valid rule of the doctrine of chances.
I will then show that Laplace’s definition of probability, first, has no meaning at all unless it be the expression of a subjective state of mind, and second, that necessary, and quite easily perceived, consequences which can be drawn from his own explanations and expositions of it are revolting to common sense.17
In order to get this matter straightened out, I think it would be well to change the place of the Sixth Paper and place it directly after the third.18 Then I would append a Correction in which I should state that the division of the elementary kinds of reasoning into three heads was made by me in my first lectures and was published in 1869 in Harris’s Journal of Speculative Philosophy.19 I still consider that it had a sound basis. Only in almost everything I printed before this century (?) I more or less mixed up Hypothesis and Induction. Hypothesis is, however, the most expressive term as well as that best supported by the historical usage of logicians, generally, for what I had in mind (rather confused by my unsound reflexions upon it).20
The general body of logicians had also at all times come very near recognizing the trichotomy. They only failed to do so by having so narrow and formalistic a conception of inference (as necessarily having formulated judgments for its premises) that they did not recognize Hypothesis (or, as I now term it, retroduction)21 as an inference. The thing was always recognized and all logicians almost (perhaps all, though the Stoics and others denied the validity of induction) distinguished induction from necessary reasoning.
When one contemplates a surprising or otherwise perplexing state of things (often so perplexing that he cannot definitely state what the perplexing character is) he may formulate it into a judgment or many apparently connected judgments, he will often finally strike out a hypothesis, or problematical judgment, as a mere possibility, from which he either fully perceives or more or less suspects that the perplexing phenomenon would be a necessary or quite probable consequence.22
That is a retroduction. Now three lines of reasoning are open to him. He may proceed by mathematical or syllogistic reasoning at once to demonstrate that consequence. That of course will be deduction.
Or he may proceed still further to study the phenomenon in order to find other features that the hypothesis will explain (i.e. in the English sense of explain, to deduce the facts from the hypothesis as its necessary or probable consequences). That will be to continue reasoning retroductively, i.e., by hypothesis.
Or, what is usually* the best way, he may turn to the consideration of the hypothesis, study it thoroughly and deduce miscellaneous observable consequences, and then return to the phenomena to find how nearly these agree with the actual facts. This is not essentially different from induction. Only it is (most usually)† an induction from instances which are not discrete and numerable. I now call it Qualitative Induction. It is this which I used to confound with the second line of procedure, or at least, not to distinguish it sharply.
A good account of Quantitative Induction is given in my paper in Studies in Logic, By Members of the Johns Hopkins University, and its two rules are there well developed.23 But what I there call Hypothesis is so far from being that, that it is rather Quantitative than Qualitative Induction. At any rate, it is treated mostly as Quantitative. Hypothesis proper is in that paper only touched upon in the last section.
There is a third kind of Induction. In order to show this, it is requisite to define Induction.
Now the essential character of induction is that it infers a would be from actual singulars. These singulars must, in general, be finite in multitude and then, as I show in my Johns Hopkins paper, the inductive conclusion can be (usually) but indefinite and can never be certain. Even if the series of singular instances, as in the case of Achilles and the Tortoise be known to hold without end, a special postulate is requisite to make the conclusion hold. [It is a distinguished merit of the strictly ordinal view of fractions that it brings this point out in perfect clearness, in conjunction with F. Klein’s doctrine of Measure (in one of the early volumes of the Mathematische Annalen).24 For there may be a discontinuity at that very point, so that e.g. 0.111111 (continued without end) does not amount to 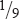
![]() , just as if
, just as if 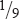
![]() and all following numbers were shoved along, which would not derange the arithmetic at all if the definitions are strictly ordinal.]‡
and all following numbers were shoved along, which would not derange the arithmetic at all if the definitions are strictly ordinal.]‡
But in ordinary cases an induction would become both precise and certain,—though even then it would not be apodictic certainty,—if the instances were of denumeral (or simply endless) multitude. Therefore, defining* induction as the sort of inference which produces verisimilitude or likelihood, that is, which regards an endless series of actualities† as conclusive evidence of a would-be since it is the best evidence possible when we are not behind the scenes.
From this point of view any plausible proposition that is supported by instances in every respect is justifiable so long as one keeps on the alert for the first exception. Of course, such an induction has the very minimum of likelihood, yet it has some; and we very often find ourselves driven to accept it. The world has always turned on its axis so far as we know about once every 24 hours and therefore we presume‡ (vaguely) that it always will continue to do so. In every case that has been sufficiently inquired into, every human being has been born of a woman not a maiden. So almost everybody feels sure it always will be found so. People are far more confident of it than they have any right to be. All former generations of men have died off. Therefore, people say, they always will. In one sense I suppose this is certain. But that they always would even if there were no accidents, seems to me as weak an inference as any that I would not positively condemn as utterly worthless. I call this kind of thing crude induction.
I must confess that although my explanation of the validity of induction seems to me to be far superior to any other, I am not altogether satisfied with it, or rather with its results.§ Quantitative Induction depends upon the possibility of making a truly representative sample. That is to say, the examples composing it must be chosen as possessing the conditional character, which is easy enough, but also so that the choice of them shall not be influenced, one way or the other, by whether or not they possess the consequent character. They must be such on the whole in that course of experience to which the induction is to be applied. That, to be sure, cannot but be the case, should the entire class sampled be alike in respect to the consequent character. But the further this ideal state of things is from being realized the more extremely difficult it becomes to get a truly representative sample, and the result, after every precaution has been taken, is that we cannot expect any great precision in inductive conclusions when the class is anywhere near being equally divided between individuals that do and that do not possess the consequent character. However, this is not owing to any falsity in my theory but to the essential imperfection of induction itself when applied to these cases.
As for the validity of the hypothesis, the retroduction, there seems at first to be no room at all for the question of what supports it, since from an actual fact it only infers a may be,—may be and may be not. But there is a decided leaning to the affirmative side and the frequency with which that turns out to be an actual fact is to me quite the most surprising of all the wonders of the universe. I hope there are few men who are so often deceived as I. They surely cannot be many. Yet I could tell you of conjectures pronounced by me with a confidence that I could not comprehend, and that were verified amazingly. I simply should not dare to tell them; I feel my credit would not support such tales: I should be a fool to expect it. So I will not enter upon that. But I will point to some of the great steps of science. Faraday was decidedly a cautious reasoner. What made him so strangely confident that electricity in all the variety of its workings never acts at a distance? What an unaccountable thing was Dalton’s atomic theory and its ready reception. What in the world should prevent,—even if there were atoms,—197 atoms of one substance from joining 719 of another, to make a chemical compound, both numbers being prime? That question prevented me, as a boy, from believing in atoms; and I was only convinced when new facts were discovered. How was it that Galileo, after glancing at one pretty evidently absurd hypothesis, at once struck upon the idea that the speed of a falling body increases uniformly with time? I am ashamed at being obliged to confess that this volume contains a very false and foolish remark about Kepler. When I wrote it I had never studied the original book as I have since. It is now my deliberate opinion that it is the most marvelous piece of inductive reasoning I have been able to find. J.S. Mill says it was not reasoning at all, but only description.25 But that only shows that he had not the slightest idea of the problem. There may be nineteen hypotheses in the book, though I cannot now say how I made out that number. But there are certainly nothing like that number to explain any one the numerous circumstances of the motion of Mars which Kepler* succeeded in reducing to order. The facts he had before him were simply observations of the place of Mars† in the heavens at various dates. His problem, as Mill seems to suppose was not simply to draw a line on the celestial globe, through all these points, and to see that that line was an ellipse with the sun at one of the foci. For, to begin with, Mill seems to forget that Kepler told where Mars was at every time in space with its three dimensions, and not merely, what the projection of its path upon the celestial sphere was.*
A pretty good example of a retroduction is the case of stopping an unknown person in the streets of a large city, asking some bit of information and crediting it. What makes this a more characteristic case is that one will have selected the man to interrogate, and will have made the selection almost without being conscious of having done so.
The justification of retroduction is that one must trust one’s instincts through life or be content with a passivity that cannot content him.
All positive knowledge must be reached if at all by an operation that begins with a conjecture. I do not mean that one reflects upon this at the outset, I mean that afterward when one subjects one’s behaviour for the day or for any other marked period to self-criticism this is how one ought to vindicate good retroductions.
As for deduction, Kant gave the principle of that. In the premises the conclusion is, in substance, asserted.
The practical lesson that experience with retroductions ought to teach men,—especially male men,—is that there is much to be learned from one’s instincts, and that consequently pains should be taken to let them develope in directions in which they prove to be sound, and to correct them in the directions in which they have proved treacherous.
The universe which man inhabits, the Real Universe, is the Universe of his conclusions, such as they would be, if properly corrected and if duly enlarged by new experiences. This is the true Kantian doctrine.26
Often we ought to put much faith,—or, at the very least, high hope,—in ratiocinations wholly unsupported by inductions—i.e. by positive evidence, (positive meaning pragmatistic, but with emphasis on the restraining tendency of experience). If one feels a strong inward tendency to hope for a future life of activity, work, further enlightenment, it is bad logic not to yield to it, while remembering that it is but a justifiable hope, and while on the watch to note whether it is really doing us good or not. Nothing has been a greater curse to a large part of the human race than religions that have been outlived. At the same time they may be keeping the ruder part of the community from crime and ruin, they may be undermining the characters of a higher class, who ought to remember that they are of the stuff that dreams are made of.27 That they have been worked over with a view to squeezing money out of the laity to support a despicable clergy. Fortunately no protestant congregation is yet rich enough to answer to this description. Whether or not the Mormons, the “Christian Scientists,” the Romanists, the Spiritualists do or do not, it is not my business to say. They are all loaded with gold or keenly in quest of it. Religions are wholesome while they are poor and persecuted.
I want to put into the volume a sufficient refutation of Mill’s system of Logic. To begin with it falls into the fatal error of Nominalism. Now how hard it is to form an exact and true definition of Nominalism, is shown by my own treatment of Gray’s stanza ten years after I had declared myself a Realist (in the sense in which we call most of the scholastics realists, or say “a scholastic realist.”)28
Nominalism might from the etymology of the name be supposed to consist in holding “would-bes” to be as the general nature of names.
But it ought not to remain long in doubt that a would-be is something that can be appropriately clothed in words or thoughts, that it is, or would be, applicable to singular actuals, and that it has a meaning, that is, is capable of definition, or logical analysis. Now these are the essential characteristics of a particular kind of sign.29
A sign in general is 1st something Real, that is 2nd applicable to an object different from itself and already known to the person to whom it is a sign, and 3rd is capable of interpretation in the mind of that person, so that it will (or would if accepted as veracious sign)* have some effect upon him of a kind that it was calculated or fit to have.30
Signs in general I divide in ten ways.31 One of these divisions is according to the substance, or mode of being, of the sign itself. For a sign may be, 1st an existent thing or actual occurrence, 2nd it may be a would-be, or habit, 3rd, it may be a mere can-be.32
Then there are 3 divisions that relate to the Object. One according to the form under which the Sign presents its Object.33 This is of course the object as the sign represents it, i.e. the Immediate Object. There are two divisions that concern the Real Object.34 One according to the Mode of Being of it, according to which the Sign will be Abstract, Concrete, or the Sign of a Habit, or would be. The other according to the relation, or connexion between the Sign and the Real Object, making the sign either an Icon, an Index, or a Symbol.
There are then 6 divisions of signs that refer to the Interpretant. Now we can regard the Interpretant in 3 ways, or rather there are 3 distinct things which may properly be regarded as the Interpretant.35 For any thing that the sign, as such, effects may be considered as the Interpretant. And this may be 1st something merely subjective, the vague determination of consciousness effected by the sign, 2nd the actual event that some signs by virtue of really acting as such bring about. For instance, let the sign be a military word or command. Then the instant action of the whole rank of men addressed will be the Dynamical Interpretant, as I call it. The third sense in which we may properly speak of the Interpretant is that in which I speak of the Final Interpretant meaning that Habit in the production of which the function of the Sign, as such, is exhausted.
I only make use of one division according to the 1st of the above, the Initial Interpretant, as I call it.36 This relates to the number of independent respects in which the sign is indefinite, that is respects which the sign points out but leaves indefinite. For example, the main difference between the verbs “is beneficial,” “benefits,” “gives,” and “sells” is of this nature.
I recognize 2 distinctions referring to the Dynamical, or Actual, Interpretant. First as to its Nature as Feeling, Action, or Affective habit, and then as to the manner in which the sign makes its appeal, as Imperative, or calling for Assent, or submitting to consideration. Then I take account of 3 divisions referring to the Final Interpretant. 1st according to the nature of its Purpose, 2nd according to the nature of the influence the sign is intended to exert, and 3rd according to the nature of the assurance the sign affords to an interpreter that has rightly apprehended it. The last 3 divisions are especially logical in the ordinary idea attached to that word.
Of course there are any number of other distinctions which a student of signs may occasionally have to attend to, but I think that these ten are as many as an ordinary Intellect can carry ready for.*37
NOTES
1. In this letter, as in chapters 7 and 8, Peirce seeks to recombine the first two Illustrations articles into a single essay. As he puts it in the July letter: “The first two constitute one Essay upon what I call Pragmatism or the doctrine of pragmatic clearness which consists in a clear conception of that Habit of Conduct in which any given concept would work out its actualization” (RL 77:229).
2. Entirely determined being.
3. The reference is to manuscripts R 643–50, composed between December 12, 1909 and August 5, 1910.
4. See chapters 7 and 8 for a sampling of this. For a more detailed discussion of this period, see the introduction.
5. “Pearson’s Grammar of Science. Annotations on the First Three Chapters.” Popular Science Monthly 58 (January): 296–306. Alternatively, Peirce suggests that this paper could be published “either in whole or omitting the first four and a half or five pages” (RL 77:247).
6. Peirce initially wrote the first two articles as a single essay. In chapters 7 and 8 Peirce seeks to recombine them. Peirce’s original discussion of Gray’s stanza is found above in chapter 2, sect. IV.
7. See also chapter 2, sect. I, with endnotes. The latter refer to R 254 (ca.1895) where Peirce separates sensuous from logical clearness and gives an extensive analysis of what the first grade of (sensuous) clearness for a color amounts to (R 254:4–6).
8. Peirce’s early scientific work in astronomy, which culminated in his 1878 Photometric Researches (Leipzig: Wilhelm Engelmann), required him to make very precise color differentiations. See also W5, item 122, “On Small Differences of Sensation.”
9. See the fifth lecture of Peirce’s 1898 Cambridge Conference Lectures; see esp. RLT:182–87.
10. See esp. R 643–50. Note, though, that Peirce’s earlier work for the Century Dictionary too has a strong focus on the second grade of clearness.
11. Pierre Simon, marquis de Laplace, Théorie analytique des probabilités (Paris: Ve. Courcier, 1812) and John Stuart Mill A System of Logic, Ratiocinative and Inductive (London: J.W. Parker, 1843). For an extensive discussion of Mill and Laplace, see esp. chapter 7, version II.
12. The existential graphs refer to a way of doing mathematical logic that is geometric rather than algebraic. For Peirce’s discussion of the graphs, see esp. CP 4.347–584 (1902–1908) and RLT:146–64 (1898). For what Peirce might have had in mind with this “short and easy account,” see his discussion of the graphs in his June 22. 1911 letter to J.H. Kehler (NEM 3:159–210, esp. 3:162ff). For an accessible introduction to the graphs, see Don Roberts, The Existential Graphs of Charles S. Peirce (The Hague: Mouton, 1973).
13. Peirce spent considerable energy on the axiomatization of numbers. See esp. “On the Logic of Number,” which appeared in the American Journal of Mathematics in 1881 (W4, sel. 38). For other, unpublished, texts see e.g. “The Axioms of Number” (W4, sel. 24; 1880), “Fundamental Properties of Number” (W5, sel. 45; 1886), “Logic of Number” (W6, sel. 21; c.1887), and CP 4.153–58 (from “Recreations in Reasoning”; R205, ca.1897).
14. Laplace, Théorie analytique des probabilité, iv–viii.
15. An extensive traditional definition for probability, authored by Peirce, is found in CD:4741, esp. sub 2, which concerns what Peirce here calls “mathematical probability” (Peirce authored 1–3).
16. The doctrine that there is real chance in the world Peirce named tychism (W8:135). See especially his Monist article “The Doctrine of Necessity Examined” (W8, sel. 24), and his “Reply to the Necessitarians. Rejoinder to Dr. Carus,” which also appeared in the Monist. The latter, together with assorted documents and the two papers by Carus that Peirce is responding to will be included in W9 as sel. 42–49.
17. Some of those consequences are discussed in chapter 7.
18. Given that Peirce also suggests combining the first two articles into a single essay this suggestion is somewhat ambiguous. It can mean moving “Deduction, Induction, and Hypothesis” between “The Doctrine of Chances” and “The Probability of Induction,” which is what the editors of the Collected Papers suggest (CP 8.227n), or it can mean that Peirce wants to switch “Deduction, Induction, and Hypothesis” with “The Order of Nature.” Note that “The Doctrine of Chances” and “The Probability of Induction” also originated as a single paper (see the headnote to “The Doctrine of Chances,” as well as the introduction to the present volume).
19. The “first lectures” are the Harvard lectures of 1865. See esp. “Lecture VIII: Forms of Induction and Hypothesis” (W1, sel. 33). Though Peirce refers here to his 1869 “Grounds of the Validity of the Laws of Logic: Further Consequences of Four Incapacities,” which is the third paper in a series of three, the reference should have been to the second paper, “Some Consequences of Four Incapacities” Journal of Speculative Philosophy 2 (1868): 140–57; also W2, sel. 22, see esp. W2:217–20. William T. Harris (1835–1909) was the journal’s editor.
20. On the historical usage of the term hypothesis, see Peirce’s longish footnote at W2:218f.
21. Meaning literally “to draw back” (the Latin retro meaning “back” and ducere meaning “to lead”) retroduction reasons from consequent to antecedent (EP2:441, 1908). Following Giulio Pacio’s translation of Aristotle’s ápagogè in Bk 25 of the Prior Analytics, Peirce also calls this type of inference “abduction” (“leading away”; from the Latin ab, for “away,” and ducere, for “to lead”). See CD:9; the description sub 2 is Peirce’s.
22. Compare with the following from the 1903 Harvard Lectures on Pragmatism, which is the passage most often quoted by contemporary philosophers of science (CP5.189):
Long before I first classed abduction as an inference it was recognized by logicians that the operation of adopting an explanatory hypothesis—which is just what abduction is—was subject to certain conditions. Namely, the hypothesis cannot be admitted, even as a hypothesis, unless it be supposed that it would account for the facts or some of them. The form of inference, therefore, is this:
The surprising fact, C, is observed;
But if A were true, C would be a matter of course,
Hence, there is reason to suspect that A is true.
Thus, A cannot be abductively inferred, or if you prefer the expression, cannot be abductively conjectured until its entire content is already present in the premiss, “If A were true, C would be a matter of course.”
23. Studies in Logic (Boston: Little, Brown, and Co., 1883) was edited by Peirce. The paper referred to, “A Theory of Probable Inference,” is found at pp. 126–81, and is accompanied with two appendices, “Note A” and “Note B” (pp. 182–203). All three are reproduced in W4, sel. 64–66.
24. In “Über die sogenannte Nicht-Euklidische Geometrie” (Mathematische Annalen 4 [1873]: 112–45) Felix Klein argues that with non-Euclidean geometry we need not alter our notions of straight lines and planes if we extend our notion of measurement.
25. John Stuart Mill A System of Logic, 8th ed. (London: Longmans, Green & Co., 1872), Bk. III, ch. ii, sect. 3.
26. In a February 5, 1911 letter to Lawrence Lowell Peirce phrases it thus: “So far, we must admit that Kant’s notion of the limits of human understanding has a truth in it. It is not the absolute universe that man has a power of knowing, but only the special universe of human science. Within that universe what seems to man reasonable has a certain likelihood of being true for that universe” (RL 256).
27. Shakespeare, The Tempest Act 4, Scene 1, 156–57.
28. See “How to Make Our Ideas Clear,” sect. IV. Earlier confessions of to a Scotistic or scholastic realism are found at the conclusion of his 1868 “Some Consequences of Four Incapacities” (W2:238–42) and in his 1871 review of the Fraser edition of Berkeley’s Works (W2:468–69).
29. What follows is a short account of Peirce’s semiotics, or his “doctrine of signs.” For an accessible introduction to this doctrine, see James Liszka, A General Introduction to the Semeiotic of Charles Sanders Peirce (Bloomington: Indiana University Press, 1996). A far briefer and more rudimentary account can be found in Cornelis de Waal, Peirce: A Guide for the Perplexed (London: Bloomsbury, 2013), Chapter 5.
30. Over the years Peirce gives various definitions for sign, all invariably triadic. To give one example, in a 1909 letter to William James, Peirce writes: “A Sign is a Cognizable that, on the one hand, is so determined (i.e., specialized, bestimmt) by something other than itself, called its Object . . . while, on the other hand, it so determines some actual or potential Mind, the determination whereof I term the Interpretant created by the Sign, that that Interpreting Mind is therein determined mediately by the Object” (EP 2:493).
31. For other discussions of the tenfold division see CP 2.254–63 and Peirce’s correspondence with Victoria Lady Welby (esp. EP2:483f). The three division allow for only ten classes of signs as some combinations are not possible. For instance, a qualisign can only be iconic, as it cannot point at anything beyond itself; it can only display some quality of the sign. The following classification is found in CP 2.254–63:
32. Compare with EP2:484.
33. As Peirce puts it two years earlier in a letter to Victoria Lady Welby: “It is usual and proper to distinguish two Objects of a Sign, the Mediate without, and the Immediate within the Sign. . . . The Mediate Object is the Object outside of the Sign . . . The Sign must indicate it by a hint; and this hint, or its substance, is the Immediate Object” (SS:83, 1908).
34. Peirce also calls this the dynamical object, preferring the latter term because there are situations where this so-called real object “is altogether fictive” (EP2:498, 1909). It is the object “which, from the nature of things, the Sign cannot express, which it can only indicate and leave the interpreter to find out by collateral experience” (ibid).
35. The distinction drawn is between the immediate, the dynamical, and the final interpretant.
36. Peirce most often calls this the immediate interpretant; other designations are emotional interpretant and impressional interpretant.
37. In addition to his ten-fold classification, which is a product of three trichotomies, Peirce also devises a table of twenty-eight classes of signs, based on six trichotomies, and a table of sixty-six classes of signs, based on no less than ten trichotomies (EP2:481). The reduction to sixty-six classes of signs is considerable, as ten trichotomies can be combined in no less than 59,049 ways (id). See also Irwin Lieb’s account of Peirce’s classification of signs (SS:160–66).
![]()
*The first part of this letter is transcribed from the typescript that was made at the Open Court Publishing Company, taking into account Francis Russell’s corrections to the typescript. For this part the original holograph is lost, with the exception of one page (see next footnote). A later footnote indicates where transcription from the holograph begins.
* error is its nominalism … and conversely.] Transcribed from RL 77:220.
*From this point onward the transcription is made from Peirce’s original holograph letter as it is preserved at the Houghton Library.
†Marginal note by Peirce: I am not satisfied with the third. I would rather suggest the phrase “so it would appear.”
* 216] above deleted: 3600
* to being] before deleted: not greater [above deleted: less] than 2 (the ratio changing say from 21:10 to 21:11) or changes the other way
† comes to 2] above deleted: reaches
*series] before deleted: it will
† would] above deleted: will
* cardinal] interline insertion
† ratios] above deleted: ordinals
‡ rational] interline insertion
§ positive] interline insertion
** ratios] after deleted: successive
†† same] above deleted: any
* p:q < (p+r):(q+s) <r:s] emended from: p:q < (p+r):(q:s) < r:s
† 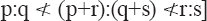
![]() emended from:
emended from: 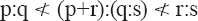
![]()
‡ of real grades] interline insertion
* usually] interline insertion
† (most usually)] interline insertion
‡ ordinal.]] closing square bracket added by the editor
* defining] before deleted: verisimilitude, or likelihood, as the sort of approach to perfect certainty that a sound induction possesses,
† of actualities] interline insertion
‡ presume] above deleted: suppose
§ , or rather with its results] interline insertion
*Though throughout this text Peirce mostly wrote Kepler at this instance he wrote Keppler, a spelling he preferred because it is how Kepler signed his name in his correspondence. See W8, sel. 49 and W8:452; see also R 339d:581 (1908).
† Mars] before deleted: relatively to the different stars at many di
*Peirce inserted, centered in the white space following the end of the paragraph “Aug”, which suggests that he did not complete the letter on August 23. Though Peirce neglected to mention the day, it can be conjectured that he continued the letter either the next day (i.e., the 24th) or shortly thereafter, as in an unsent cover letter dated August 26, 1910 Peirce mentions “a long letter that should have gone two days ago” (RL 77:252–53).
*Closing parenthesis added.
*With its period lacking this sentence concludes the letter, which is unsigned. The typescript made at the Open Court confirms that this is the end of the letter that Peirce had sent them.