Nos últimos anos que antecederam a minha aposentadoria como professor de Física, lecionei várias disciplinas básicas, cujas ementas consistiam numa introdução à mecânica newtoniana. Normalmente estas disciplinas são ensinadas sem quaisquer referências aos fatos históricos e filosóficos que antecederam a obra de Newton, tida como marco zero da mecânica, e de fato, assim também a lecionei durante anos a fio. Constatei, entretanto, na última década de atividades em sala de aula, que uma introdução à mecânica, nos moldes que farei neste capítulo, aguçou enormemente o interesse dos aprendizes, que passaram a ver a mecânica newtoniana inserida num contexto histórico mais amplo, e ainda os capacitou para um melhor e mais profundo entendimento das próprias leis da mecânica. Elas não foram mais vistas como meras fórmulas operacionais “inventadas,” num lampejo isolado, por Newton, para resolver problemas específicos, mas formas de expressão matemática de um discurso científico que passou a vigorar antes mesmo da existência do físico inglês. Constatei também, ao longo de minha travessia por várias universidades onde lecionei, que as leis de conservação de energia e momentum, quando apresentadas dentro de um contexto histórico que as remete aos pré-socráticos na sua busca do arché primordial, estimula os aprendizes ao pensamento historicamente contextualizado, bem como lhes abre novos horizontes para uma reflexão filosófica possível dentro dos limites da Física e da Ciência. No entanto, como alertei na introdução deste livro, a caracterização do emaranhamento da Ciência com a Filosofia, ainda que altamente recomendável do ponto de vista pedagógico, por lhe captar a essência, não deve ser feita em detrimento da capacidade de cálculo dos estudantes. Esses dois elementos pedagógicos, a saber, os estímulos à reflexão filosófica e à fluência na linguagem matemática deverão seguir par e passo, devendo o mestre fecundar a mente de seus aprendizes, aguçando-lhes o interesse histórico e filosófico, bem como aptidões e capacidades para a previsão precisa dos fenômenos naturais. Isso deverá ser feito não necessariamente com finalidades técnicas específicas, mas principalmente por ser a previsibilidade, a essência da Ciência que passa a viger a partir do Renascimento, com o advento da matematização do discurso científico introduzida por Kepler, Galileo, Descartes e Leibniz. Acredito também que a filosofia spinozista, que tem na causalidade imanente às leis da natureza, um de seus núcleos essenciais, aponta também para essa mesma direção pedagógica.
Vimos no capítulo anterior que na metafísica spinoziana as leis da natureza são as relações atemporais de repouso e movimento que ordenam como “códigos” a forma com que são produzidas, e arranjadas, as coisas singulares e transitórias. Vale a pena, pois investigar historicamente as leis da Física mais a fundo, dando-lhes uma contextualização filosófica, raramente apresentada nos textos e nos cursos de Física básica, o que, a meu ver, pode ter interessantes desdobramentos pedagógicos. Com isso em mente, pretendo abordar neste capítulo as grandes contribuições dadas por Descartes e Leibniz para o estabelecimento das leis de conservação da natureza, expressas matematicamente.
Embora a metafísica de Spinoza seja muito distinta dos sistemas criados pelos dois pensadores acima citados, eles parecem convergir para um ponto comum: a natureza pode ser descrita matematicamente por leis eternas e universais, que descrevem a conservação de algo que lhe é essencial. Enquanto que para Spinoza, essas leis são os modos infinitos da substância infinita1, ou seja, leis da natureza naturada, para Descartes são as formas com que um Deus transcendente construiu o mundo. Já para Leibniz, era necessário buscar uma grandeza física com a qual Deus proveria as mônadas de uma força motriz essencial, a vis viva2. Pelos motivos expostos, parece-me importante dedicar este capítulo ao estudo das leis naturais que são aquilo que permanece na mudança, na necessidade de seu curso, pois é na percepção da regra e da lei que os fatos, que de outra forma são apenas acidentes, se tornam claros.
Pretendo assim descrever neste capítulo a gênese dos princípios de conservação da natureza, como o da energia e do momentum linear, conjeturando que tiveram a sua origem nos mitos de criação do Universo, estando também presentes nas ideias dos filósofos pré-socráticos. Com o racionalismo do séc. XVII, a partir de Descartes e Leibniz, estes evoluem para expressarem-se na forma de leis matemáticas. Segundo Heidegger3, um novo ideal renascentista de matematização da natureza, decorrente de uma nova disposição do homem frente a ela, possibilita a experimentação, e não ao contrário, como normalmente se supõe nos meios científicos mais conservadores. Discutirei então que tanto a conservação da grandeza mv, preconizada por Descartes, quanto da grandeza mv2, preconizada por Leibniz, antes tidas como excludentes, galgaram a condição de leis universais coexistentes e complementares.
As primeiras concepções sobre a origem do universo foram os mitos cosmogônicos, como o Gênesis bíblico e o Enuma Elis babilônico, que já descreviam o início do universo como obra de um ou vários deuses que ordenaram o caos inicial, através de uma separação das coisas que, logo em seguida passavam a existir, ganhando um nome. A matéria-prima era assim o caos que se transformava pela ação divina numa série de coisas nomeadas. A partir do séc. V a.C., na Grécia, a mitologia foi sendo substituída por uma visão filosófica na qual o universo era construído a partir de um elemento primordial, o arché, que poderia ser a água, segundo Thales, o ar, segundo Anaxímenes, ou o apeyron (indefinido em grego), segundo Anaximandro. Empédocles propunha a teoria dos quatro elementos primordiais: terra, ar, fogo e água, que se transformavam, sob a ação de duas forças, Amor e Ódio, gerando tudo o que existe. Os atomistas sustentavam, conciliando a imutabilidade do ser de Parmênides com o eterno vir-a-ser de Heráclito, que a diversidade e a mutabilidade das coisas existentes no Universo poderiam ser explicadas através da combinação de elementos imutáveis e indivisíveis, os chamados átomos, e que além disso “nada surge do nada,” mas tudo surge de uma (re)combinação atômica.
Neste ponto, é importante que o mestre faça seus aprendizes notarem que todas essas antigas concepções já continham em si o embrião da ideia de conservação de algo primordial que é indestrutível. Para os gregos, somente a imutabilidade poderia representar o atributo da perfeição divina e, vice-versa, o que é perfeito, não poderá jamais mudar sob o risco de perder a sua condição. Os princípios de conservação, além de meros princípios matemáticos de transformação da matéria, eram assim considerados a representação da perfeição com que foi criado o universo.
Na Idade Media, dominada pela escolástica, o universo e sua evolução obedeciam ao desígnio divino e cumpriam uma finalidade. A pergunta básica não era “por quê?” Mas, sim, “para quê?” as coisas acontecem. Um monge medieval diria que uma pedra cai para ocupar o seu lugar natural abaixo dos outros três elementos: fogo, ar e água, para assim restabelecer a ordem cósmica na qual a Terra repousa estática no centro do universo.
No século XVII, com os avanços da Ciência, ocorridos a partir de Copérnico, Kepler e Galileo, o homem passa a perceber o universo como produto de uma evolução. Esta ocorre, não mais pela ação direta de um Criador, que molda uma a uma, ex-nihilo, as suas criaturas, mas pela existência de leis universais da natureza que podem ser expressas matematicamente. Estas, sim, criadas por Deus, sendo a representação de Sua inteligência superior: trata-se de um deísmo matemático substituindo o teísmo bíblico. A questão passa então a ser colocada de uma outra forma: se Deus criou a matéria dando-lhe um sopro inicial, colocando-a em movimento, quais seriam as leis básicas que regeriam a evolução do universo? Quais seriam as grandezas que melhor representariam a matéria e seu movimento? Que expressões matemáticas melhor representariam os grandes princípios de conservação do universo? A contemplação escolástica medieval da obra divina passa a ser substituída pela pergunta: por quê? Enquanto que o para quê é a pergunta da causa final ou finalidade, o porquê é a pergunta da causa eficiente ou causalidade.
Descartes acreditava num deísmo no qual Deus criava a matéria e seu movimento, sem nenhuma interferência posterior. Nada representa melhor esta concepção do que a célebre paráfrase atribuída ao filósofo francês: “Concedam-me a matéria e seu movimento e eu construirei o Universo“
O universo todo estava assim predeterminado pelas condições iniciais com que havia sido criada a obra divina. Não havia nenhuma transcendência da matéria, além de sua extensão e seu movimento. A partir dessa premissa básica, Descartes construiu a sua complexa teoria dos vórtices, pela qual, através de uma longa rede de causas e efeitos, tenta explicar desde a origem e a evolução do universo até a formação da crosta terrestre. O filósofo francês acreditava também na existência de leis fundamentais da natureza, criadas juntamente com a matéria, e que assim foram formuladas em seu livro, Princípios de Filosofia:
Cada coisa permanece no mesmo estado o tempo que puder e não muda este estado senão pela ação das outras e cada parte da matéria jamais continua a mover-se segundo linhas curvas, mas sim segundo linhas retas4.
Se um corpo que se move encontra outro mais forte que ele, não perde nada de seu movimento e se encontra outro mais fraco, a quem possa mover, perde de seu movimento aquilo que transmite ao outro5.
A primeira lei é a do princípio de inércia que Newton formularia com mais precisão nos Principia, enquanto a segunda é uma lei geral dos choques na qual Descartes postula que: “Deus é a primeira causa do movimento, e que Ele conserva uma mesma quantidade de movimento no universo“ O sábio francês queria dizer, em linguagem moderna, que se um corpo pequeno colide com outro grande (“corpo mais forte”) ele inverte a sua velocidade, algo como uma bolinha de pingue-pongue colidindo com uma parede. E se o corpo colidir com um menor (“outro mais fraco”) transmitirá parte de sua quantidade de movimento a este segundo corpo, tal como uma raquete impulsionando a mesma bolinha de pingue-pongue.
Estava assim estabelecida a lei geral de conservação do movimento que, para Descartes, tinha a sua verdadeira medida como o produto da massa pelo módulo da velocidade do corpo, sendo assim a grandeza representativa da imutabilidade e perfeição na obra do Criador. O filósofo francês não tinha, a exemplo de Galileo, um conceito claro de massa a qual confundia com o volume6, o peso e a força do corpo, além de que seu conceito de velocidade não era vetorial e sim escalar, valendo para a conservação apenas o seu módulo.
Gottfried Wilhelm Leibniz (1646-1716), matemático, filósofo, político e historiador alemão nascido em Leipzig, pode ser considerado, juntamente com Newton, Descartes, Galileo e Spinoza, um dos maiores espíritos do séc. XVII. Sua contribuição foi imensa em cada uma das atividades em que atuou. Em matemática, sua grande façanha foi a de ter desenvolvido o cálculo integral-diferencial, independentemente de Newton, o que lhe valeu injustas acusações de plágio por parte dos seguidores do sábio inglês. Além de publicar seu trabalho antes, ele o fez, ao contrário de Newton, com a notação de diferenciais tal qual conhecemos atualmente. Filosoficamente, Leibniz criou um sistema de pensamento próprio, de certa forma contrário ao de Descartes, acreditando que, para a concepção do universo, não bastavam apenas a extensão e o movimento da matéria, mas era necessário também introduzir algumas ideias metafísicas, como o esforço, a vontade e a alma. Uma outra noção fundamental, não só do sistema filosófico de Leibniz, como de outros sistemas filosóficos racionalistas contemporâneos, foi a de causa imanente, que se expressa, segundo J. F. Mora7 causa aequat effectum, isto é, uma identidade completa entre a causa e seu efeito que neste se manifesta, exprime e esgota. Leibniz embora concordando com Descartes sobre a necessidade de exatidão nos princípios e no método, considerava indispensável devolver à Ciência certas noções que os cartesianos haviam excluído. Contra o dualismo cartesiano que opõe a matéria (res extensa) ao pensamento (res cogitans) situando-os em domínios distintos, Leibniz propõe a teoria das mônadas, espécie de átomo da espiritualidade e da força da matéria, não vendo assim nenhuma contradição entre esta e o espírito. Passa, assim, a buscar a verdadeira representação matemática da força (vis) das mônadas. Para Spinoza, como já vimos antes, também não havia dualidade porque tanto o pensamento como a extensão da matéria eram atributos da substância divina e esta era imanente à natureza e suas leis. Leibniz e Spinoza, ao contrário de Descartes, eram pensadores monistas.
Leibniz tentava também descobrir uma forma melhor de achar a verdadeira medida do movimento da matéria a qual atribuía, como Descartes, a uma força que lhe é imanente. Lembrando-se das experiências de Galileo Galilei, descritas em seu livro, “Duas Novas Ciências“8, no qual o sábio italiano concluiu que a velocidade final de corpos em queda livre não dependia do peso, mas apenas da altura da qual caíssem, compreendeu Leibniz que um objeto pesado causaria mais impacto ao atingir o solo do que outro leve, supondo ambos caindo de uma mesma altura, e adquirindo portanto a mesma velocidade final. O filósofo alemão acreditava que para medir a força: bastava encontrar uma maneira de medir o impacto causado pelo corpo. Esse, por sua vez, de acordo com o princípio de identidade entre causa e efeito, confundir-se-ia com a própria força, pois que esta seria imanente ao impacto É, pois, importante notar que, para a filosofia leibniziana, a força e o impacto que faz, por sua vez, o corpo erguer-se novamente, eram um par constituído pela causa imanente e o correspondente efeito que a exprime. Assim, a força descendente, o impacto e a nova força ascendente formariam uma tríplice cadeia de causas imanentes e efeitos.
Em 1686, Leibniz em sua obra “Discurso de Metafísica“ estuda mais profundamente a física dos choques, reformulando os conceitos cartesianos, aos quais passa abertamente a criticar:
Freqüentemente nossos novos filósofos se servem da famosa regra em que Deus conserva sempre a mesma quantidade de movimento do universo. De fato isto é muito plausível e antes eu próprio a tinha como indubitável. Porém há algum tempo reconheci em que consiste o seu erro. O Senhor Descartes e muitos hábeis matemáticos têm acreditado que a quantidade de movimento isto é a velocidade multiplicada pela magnitude (massa) do móvel é exatamente a força motriz ou, para falar matematicamente, que as forças estão na razão direta das velocidades e das magnitudes (…)9.
A seguir, Leibniz nos demonstra que a massa10 vezes a velocidade não deve ser a verdadeira medida de uma “força” e sim a massa pelo quadrado da velocidade.
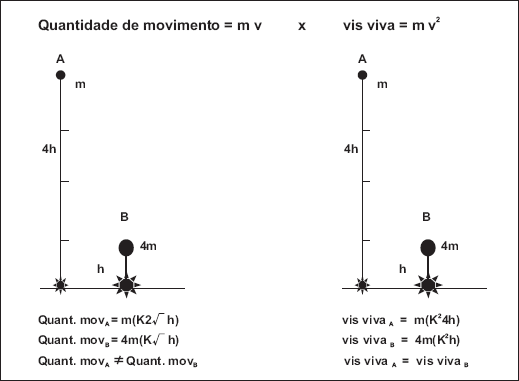
Seu argumento básico é que um corpo A de massa quatro vezes menor que a de um corpo B, porém caindo de altura quatro vezes maior, ao colidir com o solo deve ter uma força igual. Galileo e Torricelli já haviam descoberto que as velocidades finais de um corpo em queda livre eram proporcionais à raiz quadrada da altura e assim o corpo A, quando tocasse o solo, teria uma velocidade apenas duas vezes maior que a do corpo B, o mesmo acontecendo com sua quantidade de movimento. No entanto, a razão entre as velocidades deveria ser de quatro para um e assim Leibniz prova que a grandeza que mede o movimento e, portanto, a verdadeira medida da força é a massa vezes o quadrado da velocidade, isto é, mv2, e não mv (ver fig. III.1), como acreditavam os seguidores de Descartes (os novos filósofos a quem Leibniz se refere com certa dose de ironia). Na argumentação acima, é muito importante ter-se novamente o entendimento claro de que a força (vis), como causa primeira, o impacto como efeito e causa imanente de seu novo efeito, expresso na elevação do corpo, devem converter-se inteiramente um no outro, para que este assim retorne à sua altura original. Em seu Essay on Dynamics (Ensaio sobre Dinâmica), Leibniz11 escreve como seu primeiro axioma: (no ciclo completo que começa com a queda, e termina com o corpo elevando-se à altura original), “A mesma quantidade de força é conservada, ou melhor, o efeito todo é igual à causa total“ Sendo esse axioma uma exigência básica do princípio metafísico de identidade entre causa imanente e efeito12.
A grandeza mv2, nomeada de vis viva e a quantidade de movimento de Descartes mv, passaram então a disputar entre si o status de “verdadeira medida do movimento e da força de um corpo“. A questão foi, em sua época, motivo para grande discussão entre os cartesianos e os leibnizianos e tomou conta de todo círculo científico da época.
É importante esclarecer que antes do advento dos Principia de Newton, o conceito de força (vis) dos séculos XVI e XVII estava ainda impregnado de um aristotelismo escolástico do qual nem os grandes Descartes e Leibniz conseguiram se desvencilhar. Na escolástica, um corpo em movimento possuía uma vis imanente que era necessário se esgotar para que o corpo pudesse parar em seu lugar natural. A força era então a medida do próprio movimento e algo que lhe era inerente. O próprio Newton levou cerca de vinte anos, para formular a 1a lei de movimento, lutando contra a sua consciência até então impregnada de conceitos como forças inatas e vis inertiae e coisas que o valham13. Somente com a formulação completa de suas três leis do movimento é que a força começou a ser percebida como algo extrínseco ao corpo, algo que lhe é comunicado por outros corpos que estão em sua vizinhança, e que muda o seu estado. O conceito newtoniano de força é, pois, filosoficamente bem distinto da vis viva de Leibniz. Pois em Newton a força, ao contrário da vis do filósofo alemão, é causa transitória da mudança do movimento de um corpo, uma vez que nele não se origina nem se esgota pois que provém de sua vizinhança (outros corpos) que às vezes, como na força gravitacional, podem estar distantes. Segundo T. Kuhn14, a ação à distância, por não poder ser jamais uma causa imanente, foi inclusive objeto de sérias críticas e controvérsias que se prolongaram aos séculos XVIII e XIX, só sendo convenientemente esclarecida depois da invenção do conceito de campo, por Faraday e Maxwell. Em linguagem moderna, poder-se-ia dizer que só a partir das leis de Newton é que os conceitos de volume, peso, força e massa foram claramente separados e definidos. Explica-se assim historicamente o porquê da disputa na qual praticamente todos os grandes sábios do século XVII se envolveram para decidir qual era a verdadeira medida do movimento.
Em geral, os sábios italianos e alemães defendiam as ideias de Leibniz, enquanto os franceses eram quase todos cartesianos. A polêmica tornou-se áspera, e até o filósofo Voltaire dela tomou parte, do lado dos cartesianos, com seu costumeiro estilo astucioso e irônico. Depois de uma viagem à Inglaterra, ele aderiu definitivamente às ideias newtonianas, defendendo-as com o mesmo vigor que sempre caracterizou este grande pensador e polemista francês15.
O grande matemático e físico holandês, Christian Huygens (1629–1695), tido por Ernst Mach “como um autêntico sucessor de Galileo,” deu inúmeras contribuições à ciência do séc. XVII, como o princípio de propagação ondulatória da luz, que leva o seu nome; a expressão matemática do pêndulo composto, a expressão da força centrípeta, além de ter sido o primeiro construtor do relógio de pêndulo, revolucionando com esta invenção a história da medição do tempo.
Em 1669, o jovem Leibniz ainda era um cartesiano, e, portanto, estava longe de defender a vis viva como uma grandeza fundamental de sua metafísica. No entanto, Huygens, após cuidadosas observações sobre o que acontecia, quando dois objetos em movimento colidiam, já afirmava que numa colisão “entre corpos duros”, como por exemplo, entre duas bolas de bilhar, a soma das vis viva de cada uma das bolas é a mesma, antes e depois da colisão. Um corpo poderia ter a velocidade diminuída pela colisão, enquanto que a do outro aumentaria. Consequentemente, a soma das duas vis viva seria sempre a mesma. Nas próprias palavras de Huygens:
A soma dos produtos da massa de cada corpo duro pelo quadrado da sua velocidade é sempre a mesma antes e depois do encontro16.
Huygens teve assim decisiva influência no desenvolvimento das ideias de Leibniz e, segundo P. Costabel:
Leibniz, tendo não só aprendido há muito, com Huygens que a quantidade de movimento no sentido cartesiano (onde a velocidade é tomada apenas em seu módulo) não é conservada no fenômeno do impacto (…) aprendeu o papel que a elasticidade exerce na explicação das leis de impacto e finalmente entendeu também a conservação da grandeza mv17.
Num universo concebido como a evolução da matéria e de seu movimento, a vis viva passava a ser assim, graças a Huygens e Leibniz, uma séria candidata para a melhor representação matemática da matéria em movimento.
Como sabemos hoje, a vis viva, isto é, a massa pelo quadrado da velocidade de um corpo é o dobro de uma grandeza que no século XIX foi chamada por Lord Kelvin (1824-1907) de energia cinética. O termo energia vem do grego energeia, que significa “em movimento” ou “em funcionamento,” e surge para substituir a inadequada terminologia de vis ou força de Leibniz, ainda comprometida com o aristotelismo. As descobertas de Leibniz e Huygens foram assim embrionárias para a construção de um dos mais importantes princípios da Física: o da conservação de energia que só foi formulado em meados do séc. XIX num enunciado em que a energia do universo não pode ser criada nem destruída. O conceito de energia generalizou-se, então, a partir da vis viva, para abarcar todas as outras formas de energia, como por exemplo, a vis viva latente ou vis mortua, como é hoje conhecida a energia potencial. A noção de energia potencial já foi intuída por Leibniz, ao perceber que uma força que realiza um trabalho (força vezes a distância percorrida pelo ponto de aplicação da própria força), suspendendo um corpo ou contraindo uma mola, comunica ao corpo uma energia de repouso que depois poderá ser reconvertida em energia cinética. Em um processo onde não ocorram perdas de energia, através de forças de atrito consideráveis, a soma da energia cinética e potencial deve permanecer praticamente a mesma ao longo de todo o processo.
Em 1798, o engenheiro militar norte-americano Benjamim Thomson (1753-1814), também conhecido por Conde Rumford, descobriu, ao perfurar canos de canhão (para fazer as suas bocas), que o calor produzido pelas brocas era inextinguível, fervendo toda a água que era utilizada para o resfriamento. O calor que antes era considerado uma substância que passava dos corpos quentes aos frios, chamada de calórico, pelos físicos do séc. XVIII, deveria ser, portanto, considerado como uma forma de energia desorganizada que provinha da energia de movimento das brocas friccionadas pelo canhão. A partir de então, o calor passou a ser incorporado também às equações que regem o princípio de conservação da energia. Existiriam assim duas formas de se transferir energia de um sistema a outro: o trabalho das forças se encarregaria de transferir energia mecânica, enquanto o calor se transferiria por diferenças de temperatura entre os dois sistemas. No séc. XIX, a antiga vis viva de Leibniz foi assim unificada ao calor, através do conceito comum de energia, constituindo-se em uma das mais importantes leis da termodinâmica.
Esses fatos significariam assim a vitória consagradora da vis viva de Leibniz sobre a quantidade de movimento de Descartes? A quantidade de movimento do Universo, da mesma forma que a energia, também é imutável e, portanto, pode ser considerada uma grandeza fundamental da Física.
Ocorre-nos então perguntar:
Por que a natureza sempre tão econômica e parcimoniosa “escolheu” então dois princípios de conservação para representar o movimento de translação da matéria que constitui o Universo?18
Por que são necessárias duas grandezas matematicamente distintas para representar a perfeição do cosmos e de suas transformações?
Essas perguntas precisaram esperar quase três séculos para uma resposta convincente. Mais precisamente, do séc. XVII ao séc. XX, pois só puderam ser respondidas convenientemente, depois do advento da Física newtoniana ocorrida no final do séc. XVII e no início do séc. XX, com a formulação quadridimensional da Teoria da Relatividade restrita.
A força newtoniana de acordo com a segunda lei do movimento produz aceleração, isto é, mudança de movimento do corpo. Mostra-se, nos cursos de Física básica, que a ação da força ao longo do espaço percorrido é igual à variação de energia cinética do corpo, enquanto que a ação da força ao longo do tempo é igual à variação de sua quantidade de movimento. Matematicamente pode-se escrever que F.d = Δ(1/2) mv2, enquanto que F.t = Δ(mv). A energia é assim a ação de uma força no espaço (grandeza também chamada de trabalho), enquanto a quantidade de movimento é a ação da força ao longo do tempo (grandeza chamada de impulso de uma força). No séc. XX, o espaço e o tempo foram unificados e receberam um tratamento matemático indiferenciado pela relatividade restrita de Einstein, transformando-se no espaço-tempo quadridimensional que não pode ser desmembrado. Da mesma forma, a quantidade de movimento e a energia, como aspectos distintos de uma mesma essência, isto é ação da força no tempo e no espaço, são irmãs siamesas que não podem ser separadas. A energia é assim a quarta componente do movimento enquanto a quantidade de movimento (um vetor) são as três componentes espaciais. Formam juntas um quadrivetor, assim como o espaço-tempo.
A vis viva mv2 de Leibniz e a quantidade de movimento mv de Descartes, consideradas, no século XVII, como grandezas “rivais,” são hoje tratadas em pé de igualdade e consideradas ambas como representações do movimento e da transformação da matéria. Além disso, a famosa equação de Einstein de transformação massa-energia, que se expressa como E = mc2, nos diz que uma pequena quantidade de massa pode se transformar em uma imensa quantidade de energia e, vice-versa, uma grande energia pode se condensar para criar uma pequena massa. Assim, a própria energia pode ser considerada como um estado mais volátil da matéria. Massa, energia e quantidade de movimento passam assim a ser representações distintas de uma mesma realidade material. Vejamos o que o próprio Einstein tem a nos dizer:
A física pré-relativista contém duas leis de conservação cuja importância é fundamental – a lei da conservação da energia e a lei de conservação da massa, em aparência completamente independente entre si. Através da teoria da relatividade elas se fundem em um único princípio19.
Depois da Teoria da Relatividade, o Criador nem precisa mais soprar o Universo para colocá-lo em movimento, como acreditava Descartes, pois a matéria já possui em si o potencial de seu próprio movimento. Basta uma pequena fração do universo desaparecer para dotá-lo de todo o movimento necessário para a sua evolução!
O princípio da conservação da quantidade de movimento, estabelecido por Descartes, e o princípio da conservação das forças vivas (energia), estabelecido por Leibniz e Huygens, e que hoje são tidos como interdependentes e igualmente verdadeiros, são leis universais e eternas. São também as expressões matemáticas mais adequadas para representar a evolução causal do Universo, marcando dois fatos de fundamental importância na História da Ciência e na história dos princípios fundamentais da Física e da Filosofia.