12.

Le basi della musica

Tutte le melodie e le armonie

sono imbevute di numeri e di geometrie.

(Andreas Speiser)

Analogamente all’arte figurativa, anche la musica si basa su rigorosi concetti matematici, in tutti i propri aspetti (note, scale, intervalli, melodie, tempi, ritmi e armonie).

Ogni segnale acustico è generato dalle oscillazioni di un corpo elastico, le quali agendo sulle molecole dell’aria circostante, le comprimono e le lasciano dilatare ripetutamente. Il moto vibratorio così prodotto viene trasmesso da ciascuna molecola a quelle vicine, dando origine a un’onda sonora che, quando arriva a toccare il nostro orecchio, riproduce sul timpano una serie di oscillazioni, analoghe a quelle iniziali.

In base alla natura della sorgente acustica, le oscillazioni prodotte possono essere:

– periodiche, se le vibrazioni sono tutte uguali tra loro e si succedono con la stessa cadenza temporale;

– aperiodiche, se le vibrazioni si succedono con forma e cadenza irregolare.

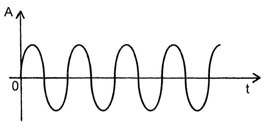
Oscillazione periodica

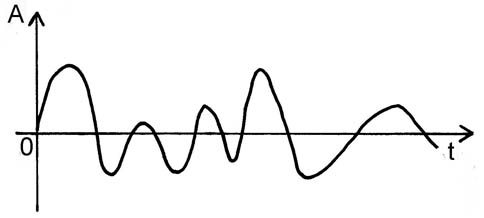
Oscillazione aperiodica

Un segnale sonoro originato da oscillazioni periodiche viene chiamato suono, perché provoca, in genere, un effetto acustico piuttosto piacevole. Un segnale sonoro originato da oscillazioni aperiodiche viene chiamato rumore, perché provoca, in genere, un effetto acustico alquanto fastidioso.

Mentre il rumore, per la sua natura indeterminata, può essere studiato in acustica solo ricorrendo a metodi statistici, il suono può essere sempre descritto esattamente attraverso caratteristiche fisiche ben determinate. In particolare, ogni suono viene individuato dalla combinazione delle seguenti tre caratteristiche fondamentali.

• Altezza: dipende dall’ampiezza in senso orizzontale delle oscillazioni dell’onda; si misura contando il numero di oscillazioni riscontrabili nell’unità di tempo; i vari suoni vengono classificati in base a tale parametro, detto frequenza, che viene espresso in Hertz (Hz). Ogni diversa nota musicale corrisponde a una diversa frequenza.

• Intensità: dipende dall’ampiezza, in senso verticale, delle oscillazioni dell’onda; corrisponde a ciò che comunemente viene denominato volume di un segnale acustico e viene espresso in decibel (dB). Una stessa nota musicale può essere emessa a diverse intensità.

• Timbro: dipende principalmente dalla forma dell’onda sonora che, in genere, ha un andamento frastagliato (e non regolare come quello indicato nell’esempio iniziale); questo parametro consente di individuare la natura della sorgente acustica. Una stessa nota musicale può essere emessa con timbri diversi.

In merito a quest’ultimo concetto, è bene precisare che i suoni rappresentati da forme d’onda regolari (denominate sinusoidi) vengono chiamati puri; tutti gli altri tipi di suono vengono detti complessi.

Nel 1822, il matematico francese Jean-Baptiste Fourier ha dimostrato che, sovrapponendo opportunamente una certa quantità di suoni puri, è possibile ricostruire qualunque tipo di suono complesso. L’odierna tecnologia consente di sfruttare questo fondamentale concetto mediante l’uso del sintetizzatore, uno strumento elettronico che consente di comporre un suono di natura qualsiasi, mediante la sovrapposizione di determinati suoni puri, generabili a piacere.

A titolo di esempio, qui di seguito è riportata la forma d’onda di un suono di pianoforte, abbinata alle principali sinusoidi, dalla cui sovrapposizione può essere determinata.

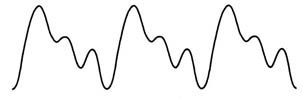
Forma d’onda di un pianoforte

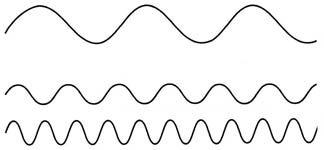
Principali sinusoidi componenti l’onda precedente

Un primo studio sistematico dei rapporti intercorrenti fra i possibili suoni venne svolto, nel V secolo a.C., dal matematico greco Pitagora, il quale si accorse, tra l’altro, che pizzicando una corda di lunghezza L si ottiene sempre un suono somigliante a quello emesso da un’altra corda di lunghezza L/2.

Questo notevole fenomeno acustico è stato rilevato, praticamente, da tutte le civiltà umane. Infatti, ogni tipo di sistema musicale, ideato in qualsiasi parte del mondo e in qualsiasi epoca, è fondato su una suddivisione dell’intervallo di frequenza, riscontrabile tra due suoni somiglianti.

In particolare, il sistema musicale attualmente in uso in Occidente si basa sulla suddivisione in dodici parti di un intervallo del genere (detto, intervallo di ottava). Ognuna delle parti così determinata viene detta semitono, mentre l’insieme di due semitoni consecutivi viene detto tono. I suoni selezionati con tale criterio, detti note musicali, vengono classificati, nell’ordine, con i nomi qui di seguito riportati, insieme alle relative frequenze usuali.

Nota	Frequenza
DO	262 Hz
DO# o Reb	277 Hz
RE	294 Hz
RE# o Mib	311 Hz
MI	330 Hz
FA	349 Hz
FA# o SOLb	370 Hz
SOL	392 Hz
SOL# o Lab	415 Hz
LA	440 Hz
LA# o Sib	466 Hz
SI	494 Hz
DO	524 Hz

Come si può notare, solo sette di queste note vengono indicate con un nome semplice; le restanti cinque vengono, invece, denominate in relazione alle note a esse limitrofe, con la convenzione che:

• # (diesis) indica l’innalzamento di un semitono della nota esplicitata;

• b (bemolle) indica l’abbassamento di un semitono della nota esplicitata.

Questi simboli vengono chiamati alterazioni, dato che indicano la modifica di un suono.

Un intervallo di dodici semitoni viene detto ottava (in quanto abbraccia le otto note di una scala, estremi compresi); lo stesso termine di ottava viene utilizzato per definire una nota che dista dodici semitoni da un’altra, verso l’alto o verso il basso.

Una suddivisione analoga a quella esaminata si può applicare a più intervalli consecutivi, ognuno dei quali compreso tra due suoni somiglianti.

Osservando la tabella precedente, si può notare anche che il rapporto tra due successive frequenze è, con discreta approssimazione, sempre costante.

Questa caratteristica è stata introdotta, verso la fine del secolo XVII, dal teorico tedesco Andrea Werckmeister e, successivamente, è stata adottata da tutto il sistema musicale occidentale.

Il valore costante calcolato da Werckmeister è uguale, in teoria a:

¹²√2 (radice dodicesima di 2).

Dato che questo valore è composto da una successione infinita, non periodica, di cifre decimali, per le applicazioni pratiche si ricorre a una sua buona approssimazione, come ad esempio: 1,059463 (ulteriormente approssimabile, in situazioni non eccessivamente sofisticate, a 1,059).

Il vantaggio principale legato a questo tipo di convenzione consiste nella possibilità di spostare una qualsiasi melodia di uno o più semitoni, ottenendone sempre un’altra di effetto analogo alla precedente. Un’opportunità del genere, estremamente comoda a livello di esecuzione, non era fornita dagli altri sistemi musicali in uso in precedenza; in particolare né da quello messo a punto da Pitagora, nel 500 a.C. circa, né da quello elaborato dal teorico italiano Gioseffo Zarlino, nel 1558.

La constatazione che la frequenza del suono emesso da un elemento rettilineo vibrante è inversamente proporzionale alla sua lunghezza, analogamente a quanto avviene pizzicando una corda, è utilizzata nella costruzione degli strumenti musicali.

A titolo di semplice esempio, se si desidera forgiare una serie di listelli in modo che i loro potenziali suoni coincidano con tutte le note comprese in una determinata ottava, il rapporto tra le lunghezze di due di questi listelli deve essere uguale al rapporto inverso tra le frequenze delle due note che a essi si intende associare.

Tenuto conto che il rapporto tra le frequenze di due note distanziate di mezzo tono è uguale a circa 1,059, è possibile ottenere una buona approssimazione di tale valore, ricorrendo alla frazione 18/17 (= 1,05882...), più comoda da utilizzare nelle misurazioni pratiche. Pertanto, si potrebbe pensare di realizzare i listelli sonori, assegnando a ognuno di essi una lunghezza uguale ai 17/18 di quello precedente. Procedendo in questo modo, però, a causa della piccola approssimazione adottata, i valori reali delle frequenze ottenute si discosterebbero sempre di più da quelli teorici.

In alternativa, quindi, è preferibile ricorrere a uno schema di rapporti, studiato in maniera tale da consentire continui aggiustamenti delle frequenze ottenibili.

Uno schema usato frequentemente è, ad esempio, il seguente (relativo alle otto note di una scala in DO maggiore), dove ogni rapporto indicato si riferisce alla lunghezza del primo listello, posta uguale a 1.

Per estendere questo schema alle note dell’ottava successiva, basta riutilizzare la stessa successione di rapporti, prendendo come lunghezza unitaria quella relativa all’ultima nota precedente (nell’esempio in questione, il DO più alto). Inoltre, è possibile inserire anche le note non appartenenti alla scala considerata, assegnando a ciascuno dei corrispondenti listelli una lunghezza uguale ai 17/18 di quella del listello dopo il quale deve essere inserito.

Xilofono a listelli

Xilofono a tubi

La stessa procedura è valida in assoluto, anche se si scelgono altri tipi di elementi vibranti. Ovviamente, degli oggetti così realizzati possono svolgere solo una funzione di divertente curiosità. Se si desidera, invece, metterli a punto, in modo che si prestino a essere suonati con l’accompagnamento di qualche vero strumento, è necessario che la frequenza del loro DO di base coincida con quella del DO di un altro strumento ben accordato (condizione che richiede una fase di preparazione un po’ più elaborata di quella descritta in precedenza).